НТСиТР_Акимов_учебник. Учебное пособие Надежность технических систем и техногенный риск
 Скачать 7.5 Mb. Скачать 7.5 Mb.
|
Надежность резервированной системыОдним из путей повышения надежности системы является введение в нее резервных (дублирующих) элементов. Резервные элементы включаются в систему как бы "параллельно" тем, надежность которых недостаточна. Параллельное соединение резервного оборудования системы Рассмотрим самый простой пример резервированной системы - параллельное соединение резервного оборудования системы. В этой схеме все n одинаковых образцов оборудования работают одновременно, и каждый образец оборудования имеет одинаковую интенсивность отказов. Такая картина наблюдается, например, если все образцы оборудования держатся под рабочим напряжением (так называемый "горячий резерв"), а для исправной работы системы должен быть исправен хотя бы один из n образцов оборудования. В этом варианте резервирования применимо правило определения надежности параллельно соединенных независимых элементов. В нашем случае, когда надежности всех элементов одинаковы, надежность блока определяется по формуле (4.5.9) Р = 1 - (1-р)n. Если система состоит из n образцов резервного оборудования с различными интенсивностями отказов, то P(t) = 1-(1-p1) (1-p2)... (1-pn). (4.5.21) Выражение (4.5.21) представляется как биноминальное распределение. Поэтому ясно, что когда для работы системы требуется по меньшей мере k исправных из n образцов оборудования, то P(t) = 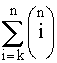 pi(1-p)n-i, где pi(1-p)n-i, где 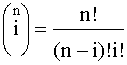 . (4.5.22) . (4.5.22)При постоянной интенсивности отказов λ элементов это выражение принимает вид P(t) = 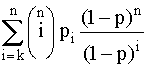 , (4.5.22.1) , (4.5.22.1)где р = еxp(-λt). Включение резервного оборудования системы замещениемВ данной схеме включения n одинаковых образцов оборудования только один находится все время в работе (рис. 4.5.11). Когда работающий образец выходит из строя, его непременно отключают, и в работу вступает один из (n-1) резервных (запасных) элементов. Этот процесс продолжается до тех пор, пока все (n-1) резервных образцов не будут исчерпаны. 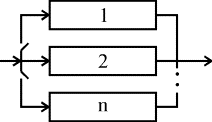 Рис. 4.5.11. Блок-схема системы включения резервного оборудования системы замещением Примем для этой системы следующие допущения: 1. Отказ системы происходит, если откажут все n элементов. 2. Вероятность отказа каждого образца оборудования не зависит от состояния остальных (n-1) образцов (отказы статистически независимы). 3. Отказывать может только оборудование, находящееся в работе, и условная вероятность отказа в интервале t, t+dt равна λdt; запасное оборудование не может выходить из строя до того, как оно будет включено в работу. 4. Переключающие устройства считаются абсолютно надежными. 5. Все элементы идентичны. Резервные элементы имеют характеристики как новые. Система способна выполнять требуемые от нее функции, если исправен по крайней мере один из n образцов оборудования. Таким образом, в этом случае надежность равна просто сумме вероятностей состояний системы, исключая состояние отказа, т.е. Р(t) = еxp(-λt) 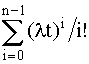 . (4.5.23) . (4.5.23)В качестве примера рассмотрим систему, состоящую из двух резервных образцов оборудования, включаемых замещением. Для того чтобы эта система работала, в момент времени t, нужно, чтобы к моменту t были исправны либо оба образца, либо один из двух. Поэтому Р(t) = еxp(-λt) 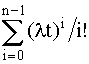 =(exp(-λt))(1+ λt). (4.5.24) =(exp(-λt))(1+ λt). (4.5.24)На рис. 4.5.12 показан график функции Р(t) и для сравнения приведен аналогичный график для нерезервированной системы. 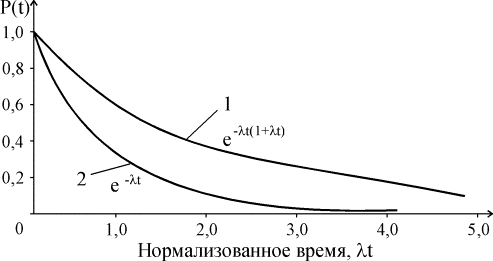 Рис. 4.5.12. Функции надежности для дублированной системы с включением резерва замещением (1) и нерезервированной системы (2) Пример 4.5.11. Система состоит из двух идентичных устройств, одно из которых функционирует, а другое находится в режиме ненагруженного резерва. Интенсивности отказов обоих устройств постоянны. Кроме того, предполагается, что в начале работы резервное устройство имеет такие же характеристики, как и новое. Требуется вычислить вероятность безотказной работы системы в течение 100 ч при условии, что интенсивности отказов устройств λ=0,001 ч-1. Решение. С помощью формулы (4.5.23) получаем Р(t) = (exp(-λt))(1+ λt). При заданных значениях t и λ вероятность безотказной работы системы составляет Р(t) = е-0,1(1+0,1) = 0,9953. Во многих случаях нельзя предполагать, что запасное оборудование не выходит из строя, пока его не включат в работу. Пусть λ1 - интенсивность отказов работающих образцов, а λ2 - резервных или запасных (λ2>0). В случае дублированной системы функция надежности имеет вид: Р(t) = ехр(-(λ1+ λ2)t) + 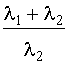 ехр(-λ1t) - ехр(-λ1t) - 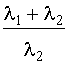 ехр(-(λ1+ λ2)t). ехр(-(λ1+ λ2)t).Данный результат для k=2 можно распространить на случай k=n. Действительно Р(t) = ехр(-λ1(1+ α(n-1))t) 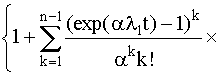 (4.5.25) (4.5.25)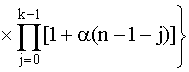 , , где a = λ2/ λ1 > 0. |
