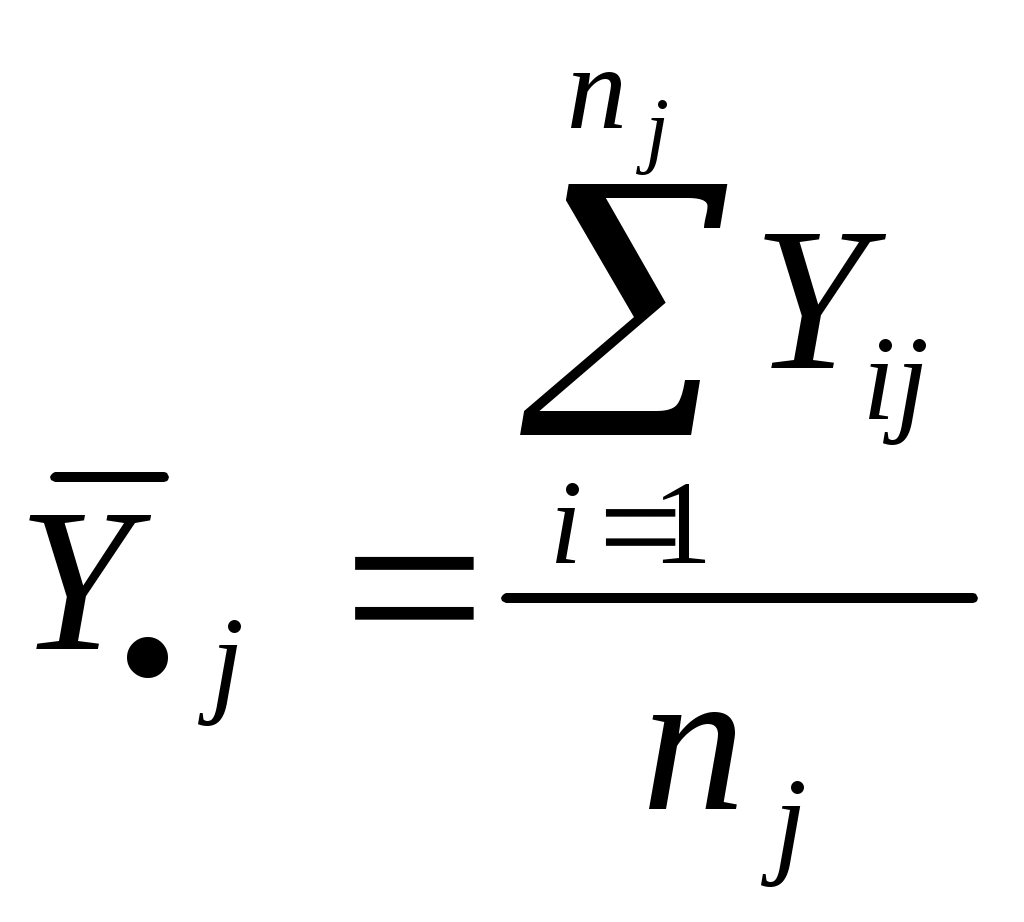Математико-статист модели в социологии. Учебное пособие оглавление введение. В основная цель курса, адресат
 Скачать 2.75 Mb.
|
Примеры задач1. Приведите примеры модельных ситуаций, когда причинно-следственные отношения могут быть установлены с помощью приведенных в главе 12 правил Милля. Приведите примеры нескольких методических задач, встающих при построении социологического инструментария (см. сноску 55 и задачу 4 из темы 10), которые можно было бы решить с помощью эксперимента и проверки статистических гипотез. Добавочная литература к главе 12 О понятии причины Аристотель. Метафизика // Аристотель. Сочинения. Т.1. М.: Мысль, 1976. С.63-367. Давыдов Ю.Н. Макс Вебер и современная теоретическая социология. М.: Мартис, 1998. С. 150-190. И.Кант. Теория познания // Антология мировой философии Т.3. М.: Мысль, 1971. С. 100-155. Лаплас. Опыт философии теории вероятностей // Вероятность и математическая статистика. Энциклопедия. М.: Большая российская энциклопедия, 1999. Милль Д.С. Система логики символической и индуктивной, изд.2. М., 1914 // Антология мировой философии. Т.3. М.: Мысль, 1971. С. 594-605. Финн В.К. Интеллектуальные системы и общество. М.: КомКнига, 2006 ЧупровА.А. Нравственная cтатистика // Брокгауз Ф.А. (Лейпциг), Ефрон И.А. (СПб.). Энциклопедический словарь. Т. XXI. С.-Петербург: Типолитография И.А.Ефрона, 1897. С. 403–408. Чупров А.А. Вопросы статистики. М.: Госстатиздат ЦСУ СССР, 1960. Юм Д. Сокращенное изложение «Трактата о человеческой природе» // Антология мировой философии. Т.2. М.: Мысль, 1970. С. 575-593. Об эксперименте в социологии Адлер Ю.П., Ковалёв А.Н. Математическая статистика и планирование эксперимента в науке о человеке // Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс, 1976. С. 477-490 Андреева Г.М. Социальная психология. М.: Наука, 1994. С.174-175 (Хоторнский эксперимент) Батыгин Г.С. Лекции по методологии социологических исследований. М.: Аспект Пресс, 1995. С. 190-227 Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс, 1976, с. 405-436 однофакторный и многофакторный дисперсионный анализ: случайные, смешанные и постоянные эффекты), с. 437-458 (Основы планирования эксперимента). Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке. М.: Мир,т.1 - 1980, т.2 - 1981 Дэниел К. Применение статистики в промышленном эксперименте. М.: Мир, 1979 Кравченко А.И. Хоторнский эксперимент //Справочное пособие по истории немарксистской западной социологии. М.: Наука, 1986. С.452-453 Куприян А.П. Методологические проблемы социального эксперимента. М.: Наука, 1971 Куприян А.П. Проблема эксперимента в системе общественной практики. М.:Наука, 1981 Кемпбелл Д. Модели экспериментов в социальной психологии и прикладных исследованиях. М.: Прогресс, 1980. Переиздано в СПб: Изд-во «Социально-психологический центр», 1996 Киш Л. Представительность, рандомизация и контроль // Математика в социологии. М.: Мир, 1977, с. 201-223. Методы сбора информации в социологических исследованиях. М.: Наука, 1990.Т.2. С. 190-214 Методы сбора данных: анализ документов, наблюдение, эксперимент. М.: ИСИ АН СССР, 1985 Методы социальной психологии. Л.: изд-во ЛГУ, 1977. С.132-150 Милграм С. Эксперимент в социальной психологии. Спб: Питер, 2000 Монсон П. Современная западная социология. Теории, традиции, перспективы. С.Пб.: Нотабене, 1992. с.160-162 (эксперимент Цимбардо) Налимов В.В. Теория эксперимента. М.: Наука, 1971 Основы прикладной социологии. М.: Интерпракс, 1996. С.68-72 Рабочая книга социолога. М.: Наука, 1983. С. 411-432 Руткевич М.Н. Макросоциология. Методологический очерк. М.: РАН, 1995. С.16-19 Статистические методы анализа информации в социологических исследований. М.: Наука, 1979. С.178-194 Хагуров А.А. Социальный эксперимент: логико-методологические и социальные проблемы. Ростов-на-Дону,1989 Хикс Ч. Основные принципы планирования эксперимента. М.: Мир, 1967 Ядов В.А. Социологическое исследование: методология, программа, методы. Самара: «Самарский ун-т», 1995. С.220-231 Blalock H.M. Causal inferences in nonexperimental research. Chapel Hill: University of North Carolina Press, 1964 О причинном анализе Бестужев-Лада И. В. , Варыгин В. Н. , Малахов В. А. Моделирование в социальных исследованиях. М. : Наука, 1978. Богомолова Е.А., Наумова Н.Ф. Структурные модели как инструмент обобщения и интерпретации социальной информации на выходе системы моделирования // Неформализованные элементы системы моделирования. М.: ВНИИСИ, 1980 Бородкин Ф.М. Об одной схеме причинного анализа // Математика и социология. Новосибирск: ИЭиОПП СО АН СССР, 1970 Бородкин Ф.М. Научный эксперимент в социально-экономических исследованиях. Дисс. На соискание ученой степени доктора экономических наук. Новосибирск, 1975 Бунге М. Причинность. М.: Изд. Иностр. лит., 1962 Волд Г. Путевые модели с латентными переменными: подход NIPALS // Математика в социологии: моделирование и обработка информации. М.: Мир, 1977. С. 241-281. Гаврилец Ю. Н. Структура связей и причинные зависимости между переменными // Математика в социологии: моделирование и обработка информации. М. : Мир, 1977. С. 135-169. Елисеева И. И. Статистические методы измерения связей. Л. : Изд-во ЛГУ, 1982. С. 97-108. (Структурные модели. Путевой анализ). Елисеева И. И. , Рукавишников В. О. Логика прикладного статистического анализа. М. : Финансы и статистика, 1982. С. 72-149 (Структурные и причинные модели). Левин К. Теория поля в социальных науках. СПб: Сенсор, 2000, с. 7-14, 178-192, 213-220 Математические методы анализа и интерпретация социологических данных. М. : Наука, 1989. С.61-94 (Выбор стратегии анализа взаимосвязи признаков) Новак С. Причинные интерпретации статистических связей в социальном исследовании // Математика в социологии: моделирование и обработка информации. М. : Мир, 1977. С. 76-123. Осипов Г. В. , Андреев Э. П. Методы измерения в социологии. М. : Наука, 1977. Осипов Г.В., Андреенков В.Г. Эмпирическое обоснование гипотез в социологических исследованиях // Социс, 1974, № 1. С. 160-173. Рукавишников В.О. Информационный подход к причинному анализу // Модели социально-экономических процессов и социальное планирование. М., 1979. Социальные исследования: построение и сравнение показателей. М.: Наука, 1978. C.104-111 (Построение показателей в процессе применения метода причинных моделей). Статистические методы анализа информации в социологических исследованиях. М. : Наука, 1979. С. 267-282 (Модели для анализа структуры причинных связей). Суппес П. Вероятностный анализ причинности // Математика в социологии: моделирование и обработка информации. М. : Мир, 1977. С. 50-75. Таганов И.Н. Информационные меры причинного влияния // Математика в социологии: моделирование и обработка информации. М. : Мир, 1977. С. 124-134. Татарова Г. Г. Структура многомерной случайной величины и проблема взаимосвязи признаков // Социологические исследования, 1986. N3. С. 142-148. Трофимов В.П. Измерение взаимосвязей социально-экономических явлений. М.: Статистика. 1975. С. 15-29 (Соотношение причинной и корреляционной связи). Хейс Д. Причинный анализ в статистических исследованиях. М. : Финансы и статистика, 1981. Blalock H. M. Causal Inferences in Nonexperimental Research, Chapel Hill: university of North Carolina Press, 1964, с. 3-60, 95-96, 172-188 Blalock H. M. Causal models in the Social Sciences, 1970 Blalock H. M. Theory construction. From verbal to mathematical formulation. Prentice hall, New Jersey, 1969, p. 1-30 Bollen, K. A. Structural Equations with Latent Variables. NY: John Wiley & Sons, 1989 Knoke D. A causal model for the political party preferences of american men // Amer. Soc. Review, 1972. P. 679-689 Spilerman S. Forecasting social events // Social indicator model, S.N.Y. 1975 Suppes P. Probabylistic Theory of Causality. Amsterdam: North-Holl P/ Co.,1970 Sage University Paper series on Quantitative Applications in the Social Sciences: n. 07-003. Asher H. Causal modeling, 1976,1980 n. 07-034. Long. Covariance Structure Models, 1983 n. 07-037. Berry W.D. Nonrecursive Causal Models, 1984 n. 07-055. Davis. The Logic of causal Order, 1985 n. 07-074. Brown, Melamed. Experimental design and analysis, 1990 n. 07-105. Finkel S.E/ Causal analysis of panel data, 1995 n. 07-114. Jaccard J., Wan C.K. LISREL Approaches to Interaction Effects in Multiple regression n. 07-135. Jaccard J. Interaction effects in logistic regression, 2001 О SEM Golob Thomas F. 2003. Structural Equation Modeling for Travel Behavior Research. Center for Activity Systems Analysis. Published in: Transportation Research, Vol. 37B, 2003, pp. 1-15. Hox J.J. Bechger T.M. 1998. An Introduction to Structural Equation Modeling. Family Science Review, 11,354-373. McArdle John J. , Johnson Ronald C. 2001. Structural Equation Modeling of Group Differences in CES-D Ratings of Native Hawaiian and Non-Hawaiian High School Students Journal of Adolescent Research, Vol. 16 No. 2, March 2001 108-149 Sage Publications, Inc. Mueller R.O. 1996. Basic Principles of Structural Equation Modeling. Springer Verlag, January. Т е м а 13 Корреляционное отношение Линейная и нелинейная связи. Границы применимости коэффициента корреляции как показателя связи между изучаемыми переменными Как известно, коэффициент корреляции Пирсона r измеряет лишь степень линейной связи между X и Y. Если он близок к 1 (или к –1), то мы можем быть уверены, что наши признаки связаны и что эта связь линейна. Близость же r к нулю может объясняться не только отсутствием связи, но и тем, что эта связь нелинейна (близость r к нулю говорит об отсутствии линейной связи). Рассмотрим таблицу 13.1. Таблица13.192 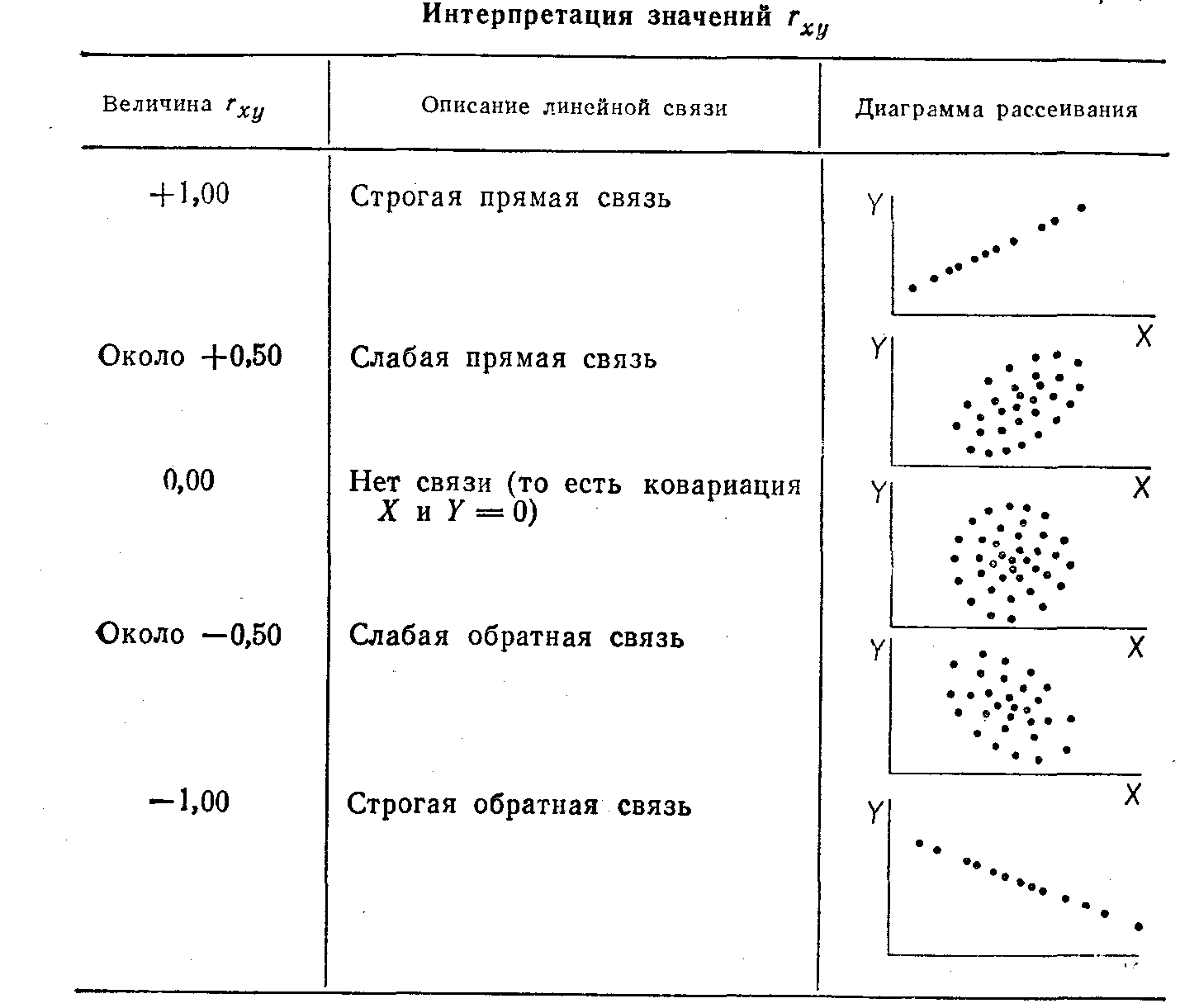 Когда коэффициент корреляции равен нулю, возможны разные ситуации: статистическая связь может вообще отсутствовать (см. рис. 13.1), а может существовать, и даже быть довольно сильной, но криволинейной ((рис. 13.2). 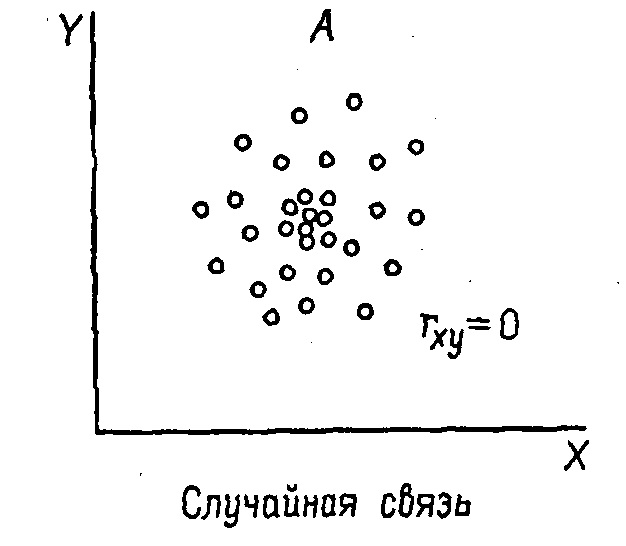 Рис. 13.1. Ситуация равенства нулю коэффициента корреляции: отсутствие статистической связи Гласс, Стэнли, 1976, с.116, рис. 7.4 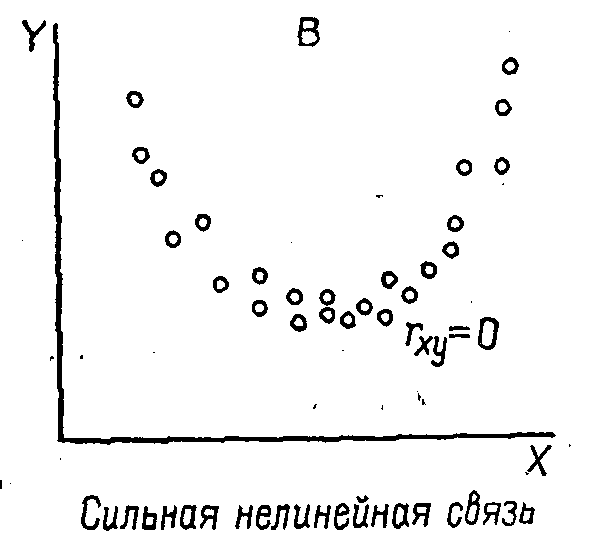 Рис. 13.2. Ситуация равенства нулю коэффициента корреляции: наличие сильной нелинейной статистической связи93 . Рассмотрим еще одну меру связи – меру, используемую для измерения связи в тех случаях, когда эта связь имеет произвольный вид, в частности, может быть нелинейной. Корреляционное отношение. Общее представление о внутригрупповом и межгрупповом разбросе Сущность новой меры связи - корреляционного отношения - продемонстрируем на примере, заимствованном из той же работы Гласса и Стэнли94. Изучается зависимость результатов ответа респондента на вопросы некоторого теста (Y) от его возраста (X). Опрашивалось 28 человек. По возрасту они были разделены на 8 групп. В представленных ниже данных каждая группа характеризуется средним возрастом попавших в нее респондентов (например, возраст 30 приписан всем людям, попавшим в возрастной интервал от 28 до 32 лет). Статистические данные представлены на рис. 13.3 и в таблице 13.2. 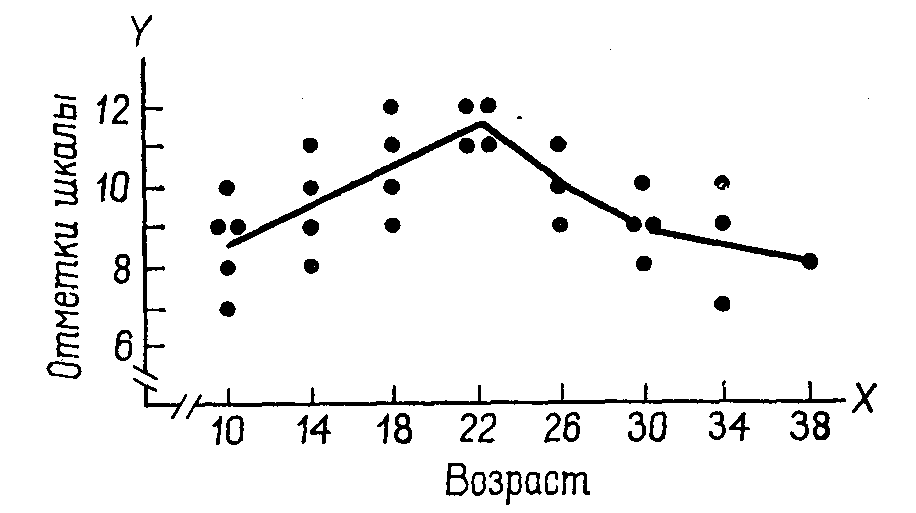 Рис. 13.3. Пример данных для расчета корреляционного отношения: связь между возрастом и характеристикой 28 людей по вспомогательному тесту цифра-знак шкалы интеллекта взрослых Векслера ( WAIS)95. Таблица 13.2. Ответы респондентов на заданный тест в зависимости от их возраста (данные для расчета корреляционного отношения)96
Yi j – значение зависимого признака для i–го респондента в j–й возрастной группе; i = 1,…,nj , где nj - число членов j–й группы; j = 1,…,J, где J – количество выделенных групп ( в данном случае J = 8). На рис. 13.3 видно, что наблюдаемые точки довольно плотно расположены вокруг нарисованной там ломаной линии. Это наводит на мысль о том, что указанная ломаная линия отражает определенную тенденцию: с изменением возраста от 10 до 22 лет показатели людей по рассматриваемому тесту растут, затем начинается спад. И говорить об этой тенденции мы можем только благодаря тому, что (1) если для каждого рассматриваемого значения возраста вычислить среднее арифметическое значение зависимой переменной, то наша ломаная линия пройдет через соответствующую точку; (2) для каждой возрастной группы разброс значений теста вокруг упомянутой средней является относительно небольшим. Это интуитивное соображение можно формализовать. Соответствующая формализация и лежит в основе рассматриваемого коэффициента связи. Введем несколько новых понятий. Обозначим через  среднее арифметическое значение зависимой переменной для j-й группы (j=1,…,J). Отметим, что точка перед индексом j в обозначении среднего арифметического означает, что по первому индексу величины Yi j произошло суммирование.ОПР. Назовем внутригрупповой суммой квадратов величину  Для нашего примера эта сумма будет равна:  (7-8,60)2 + (8-8,60)2 + (9-8,60)2 + (9-8,60)2 + (10-8,60)2 + (для первой группы)  (8-9,50)2 + (9-9,50)2 + (10 – 9,50)2 + (11-9,50)2 + … (для второй группы)   + (8-8,00)2 = 24, 87 (для восьмой группы) Обозначим через 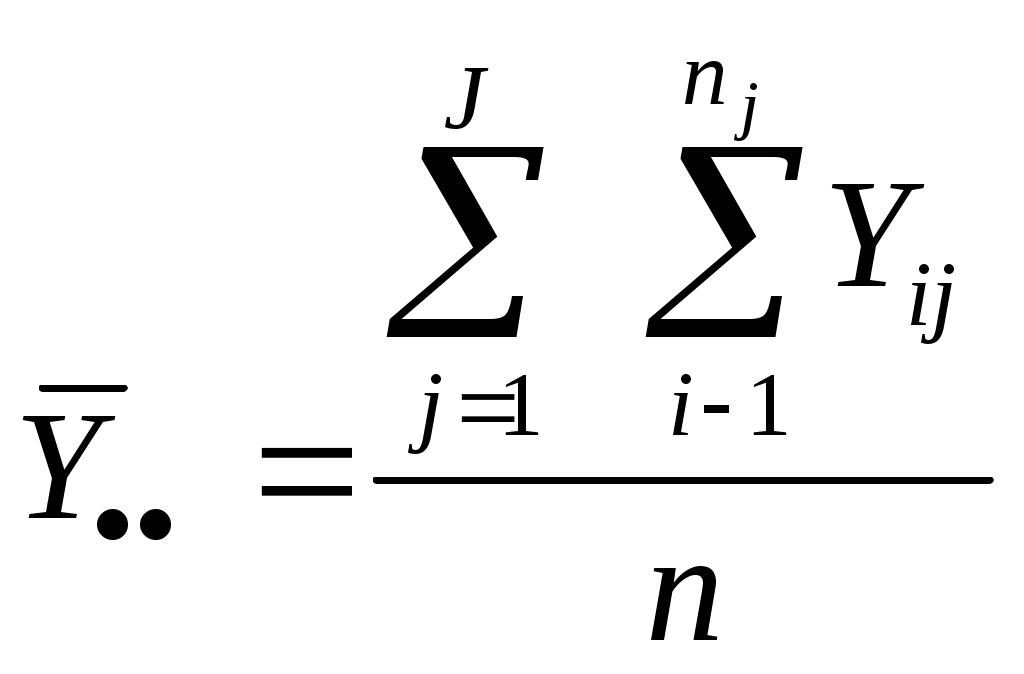 среднее арифметическое всех значений независимого признака. Очевидно, что имеет место соотношение: ,где  - объем выборки.ОПР. Назовем общей суммой квадратов величину 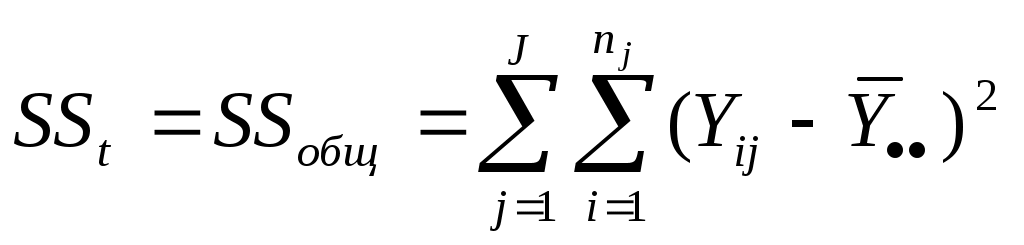 ОПР. Назовем корреляционным отношением разность 2y/x = 1 – (SS внутри / SS общ ) Для рассмотренного примера, как нетрудно проверить, имеют место соотношения SS общ = 54, 68; 2y/x = 1 – (24,87/ 54,68) = 1 – 0,455 = 0,545. Поясним смысл корреляционного отношения. Смысл любого коэффициента бывает легче понять, если рассмотреть, при каких условиях он принимает максимальное (в данном случае – 1) и минимальное (0) значение. Ясно, что 2y/x = 1, когда SS внутри = 0, т.е. когда в каждой выделенной по признаку Х группе (в нашем случае – в каждой возрастной группе) значения признака Y одинаковы. Для рассматриваемого примера это означает, что все точки лежат на выделенной ломаной линии. Ясно, что это действительно говорит о наличии криволинейной связи. Что касается равенства 2y/x = 0, то оно имеет место в том случае, когда SSвнутри = SS общ, т.е. когда фиксация признака Х нисколько не уменьшает разброс признака Y. Ясно, что это говорит об отсутствии связи: получение информации об Х не увеливает информацию об Y. Здесь напрашивается аналогия с принципом построения коэффициентов связи, основанных на прогнозных моделях (Толстова, 2000). Коэффициент 2y/x является мерой степени предсказания Y по X с помощью “наилучшим образом подобранной” линии, либо прямой, либо кривой. Заметим, что 2y/x 2х/ y (заметим, что о подобной перестановке признаков можно говорить только в том случае, если оба признака измерены по интервальной шкале; хотя для измерения одного из означенных коэффициентов, скажем,  , достаточно того, чтобы Y был интервальным, X может быть и номинальным). Поясним это на нашем примере: если человеку 10 лет, то можно довольно уверенно предсказать, что результатом тестирования для него будет балл, равный примерно 8,60. Однако если некий человек получил балл 8,60, то его возраст может быть с одинаковой вероятностью как малым (10 лет), так и большим (38 лет). Значит, можно довольно хорошо предсказать Y по X, но нельзя хорошо прогнозировать Х по Y. Это неизбежно отражается на величинах 2y/x и 2х/ y: 2y/x=0,545, а 2х/ y близка к нулю. Не будем ее вычислять. Такое вычисление потребовало бы перегруппировки данных. Ячейки должны были бы быть организованы по результатам тестирования (скажем, можно было бы сформировать три ячейки - в первую включить респондентов, получивших баллы 7-8, во вторую – баллы 9-10, в третью – баллы 11-12 ). А в качестве значений Y выступали бы возраста респондентов, вошедших в ту или иную ячейку. Приведем еще один пример. Пример. Дана частотная таблица Возраст (X) Зарплата (Y) 500-700 700-900 900-1100 18-22 10 5 5 22-26 10 10 20 26-30 5 20 20 Рассчитать корреляционное отношение 2у/х Решение. Вспомним, что, разбив диапазон изменения признака на интервалы и составив частотную таблицу, мы потеряли исходную информацию и вынуждены считать, что респонденты, попавшие в один интервал, имеют одну и ту же зарплату, отвечающую середине этого интервала. Расположим данные в более привычном (более часто использующемся при нахождении корреляционного отношения) виде. Правда, не будем выписывать конкретные зарплаты (Y) для людей, попавших в ту или иную возрастную группу (возраст – Х), а укажем, сколько человек обладают тем или иным значением. Интервал Y-ка Середина I группа (возр. 18-22) II группа (возраст 22-26) III группа (возраст 26-30) интервала 500-700 600 10 человек 10 человек 5 человек 700-900 800 5 человек 10 человек 20 человек 900-1100 1000 5 человек 20 человек 20 человек Общее среднее по Y: Y .. = (600 (10 + 10 + 5) + 800 (5 + 10 + 20) + 1000 (5 + 20 + 20)) / 100 = 880 SSобщ = (600 - 880)2 (10 +10 + 5) + (800 - 880)2 (5+10+20) + (1000 - 880)2 (5+ 20 + 20) = 2 832 000 Y .1 = (600 10 + 800 5 + 1000 5) / 20 = 750 Y .2 = (600 10 + 800 10 + 1000 20) / 40 = 850 Y .3 = (600 5 + 800 20 + 1000 20) / 45 = 866,7 SSвнутри = (600 - Y .1)2 10 + (800 - Y .1)2 5 + (1000 - Y .1)2 5 + (600 - Y .2)2 10 + (800 - Y .2)2 10 + (1000 - Y.2)2 20 +(600 - Y .3)2 5 + (800 - Y .3)2 20 + (1000 - Y .3)2 20 = 150210 + 5025 + 25025 + 250210+ 502 10 + 150220 + 26725 +67220 + 133220 = 2 449 945 2у/х = 1- SSвнутри / SSобщ = 1 – 0,845; у/х = 0,367. 13.3. Проблемы, не решаемые с помощью корреляционного отношения Корреляционное отношение так же, как и коэффициент корреляции, не решает всех вопросов, возникающих у исследователя при решении задач, связанных с изучением влияния друг на друга каких-либо двух признаков. На некоторые вопросы анализ корреляционного отношения в принципе не дает ответа. Укажем два таких вопроса. Во-первых, корреляционное отношение относится к числу т.н. интегральных коэффициентов связи. Информация по всем значения признака Х здесь как бы усредняется. Не учитывается, что разные градации могут по-разному «влиять» на Y: при одном значении X признак Y может быть жестко детерминирован, при другом – соответствующие значения Y могут быть очень разбросаны. Вопрос о том, какие именно значения Х действительно можно считать детерминирующими уровень Y, здесь не ставится. Во-вторых, использование корреляционного отношения не предполагает постановку вопроса о возможности определения уровней Y не одним, а несколькими независимыми переменными. Ответы на эти вопросы в достаточно полной мере дает дисперсионный анализ. Он будет рассмотрен ниже (Темы 14 и 15). 13.4. Соотношение между разными видами сумм квадратов Для того, чтобы идеи дисперсионного анализа легче воспринимались читателем, уже здесь введем новое понятие и продемонстрируем его сущность на рассмотренном выше примере. ОПР. Назовем межгрупповой суммой квадратов величину 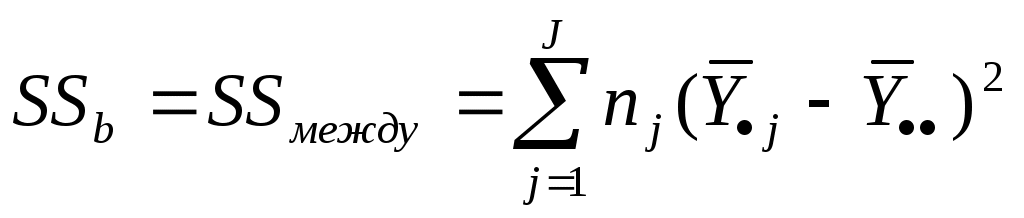 Содержательный смысл этого понятия представляется очевидным: оно характеризует величину разброса групповых средних вокруг общего среднего с поправкой, состоящей в том, что вклад в этот разброс тех групповых средних, которым отвечают более многочисленные группы, считается более сильным, чем вклад средних малочисленных групп. Нетрудно доказать соотношения: SS общ= SS внутри + SS между 2y/x = 1 – (SS внутри / SS общ ) = SS между / SS общ Как следует из приведенных формул, для определенных выше сумм квадратов могут использоваться разные обозначения (могут задействоваться начальные буквы соответствующих и русских, и английских слов): SS общ= SSt (от англ “total”); SS внутри = SSw (от “within”); SS между = SSb (от “between”) . Само сочетание SS – начальные буквы слов “sum square”. Примеры задач1. Доказать соотношение: SSb+ SSw= SSt (SSмежду + SSвнутри = SSобщ )97 2. Диапазон изменения некоторого признака Х разбили на три интервала. Их середины равны, соответственно, 10, 20 и 30. Диапазон изменения признака Y разбили на два интервала с серединами 15 и 25. Считаем, что все значения признака, попавшие в один интервал, приравниваются к его середине. Для респондентов некоторой выборки из 50 человек двумерная частотная таблица имеет следующий вид:  Середина интервала Середина интервала признака Х   признака Y 10 20 30  15 4 28 6 25 6 0 6 Рассчитать корреляционные отношения 2y/x и 2x/y Добавочная литература к теме 13. Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс, 1976. С.138-14198. Haggard E.A.Intra-class Correlation and the Analysis of Variance. N.-Y., Dryden Press,1958 Rozeboom W.W. Foundations of the Theory of Prediction. Homewood, Illinois, Dorsey Press, 1966 | |||||||||||||||||||||||||||||||||||
редние возрастных групп 
)