Математико-статист модели в социологии. Учебное пособие оглавление введение. В основная цель курса, адресат
 Скачать 2.75 Mb. Скачать 2.75 Mb.
|
ТЕМА 7Общее представление о статистической гипотезе. Проверка статистической гипотезы об отсутствии связи (критерий «Хи-квадрат») 7.1. Общее представление о статистической гипотезе. Начнем с примеров. Первый пример. Рассмотрим две дискретные переменные: X, принимающую значения из множества {1, …, r } и Y, принимающую значения из множества {1, …, c }. Мы будем их использовать как номинальные признаки, хотя вполне может быть, что их значения получены по шкалам более высоких типов. Предположим, что нам задана частотная таблица вида || n ij ||, где i = 1, … , r (raw); j = 1,…,c (column), n ij - количество объектов (например, респондентов), обладающих i –м значением признака Х и j-м значением признака Y. Обозначим также через Здравый смысл подсказывает, что независимыми признаки можно считать в том случае, когда строки частотной таблицы пропорциональны53. Можно понятие независимости признаков отождествить и с другими свойствами частотной таблицы. Нетрудно проверить эквивалентность следующих утверждений: 1  . Переменные X и Y являются независимыми. . Переменные X и Y являются независимыми.Все частоты таблицы сопряженности являются теоретическими Для всех i и j события (Х = i) и (Y = j) являются независимыми. Строки таблицы сопряженности пропорциональны. (7.1) Столбцы таблицы сопряженности пропорциональны. Все частоты таблицы сопряженности вычисляются по формуле: Предположим, что мы на основе собранной информации рассчитали частотную таблицу для некоторых двух переменных и хотим оценить, можно ли говорить о том, что связь между рассматриваемыми переменными отсутствует. Вопрос не так прост, как кажется на первый взгляд. Рассмотрим его подробнее. Вспомним, что в действительности нас интересует генеральная совокупность, хотя имеющиеся в нашем распоряжении эмпирические данные, в том числе и таблица сопряженности, обычно отвечают выборке. Мы знаем, что выборочные данные никогда стопроцентно не отвечают генеральным. Любая, даже самая хорошая выборка будет отражать генеральную совокупность лишь с некоторым приближением, любая закономерность будет содержать так называемую выборочную ошибку. Случайную погрешность. Учитывая это, мы, вероятно, будем полагать, что если столбцы выборочной таблицы сопряженности мало отличаются от пропорциональных, то такое отличие, вероятнее всего, объясняется именно выборочной погрешностью и вряд ли говорит о том, что в генеральной совокупности наши признаки связаны. Сильное же отклонение от пропорциональности заставит нас сомневаться в отсутствии связи в генеральной совокупности. Насколько же сильным должно быть такое отклонение для того, чтобы указанные сомнения у нас возникли? Наука не дает точного ответа. Она предлагает лишь такой вариант, который формулируется на вероятностном языке. Но прежде, чем ответить на поставленный вопрос, рассмотрим пример несколько иного плана. Второй пример. Предположим, что в процессе решения социологической задачи мы хотим проверить гипотезу о том, что при оплате труда работников какого-то предприятия (отрасли и т.д.) нет дискриминации этих работников по полу. Это – содержательная гипотеза. Вероятно, наиболее естественными действиями исследователя, направленными на ее проверку, будет организация некоторой выборки из работников рассматриваемого предприятия и осуществление анкетного опроса с использованием, в частности, вопроса о поле респондента и его зарплате. Затем исследователь подсчитает среднюю зарплату мужчин и среднюю зарплату женщин. Обозначим зарплату буквой х и предположим, что получены соотношения (числа условны): Хжен = 102,8; Х муж = 115,0. Далее возможны разные рассуждения. Исследователь, пытающийся доказать отсутствие дискриминации, скажет: конечно, факт есть факт – средняя заплата женщин меньше средней зарплаты мужчин, но это различие очень мало. Наверное, его можно отнести за счет того, что мы взяли не всех работников, о только некоторую выборку из них. Другими словами, можно полагать, что наша статистика не дает оснований говорить о наличии дискриминации. Другой исследователь, сторонник того, что дискриминация имеет место, выскажет совершенно твердую убежденность в своей правоте: статистические данные подтвердили его гипотезу, женщины в среднем получают меньше мужчин. Кто прав? Где та граница, то значение разности зарплат, превышение которого говорит о том, что эти зарплаты действительно можно считать разными, что они отличны друг от друга не только в выборке, но и в генеральной совокупности? Ответ получим, если воспользуемся логикой математической статистики, точнее, логикой проверки статистической гипотезы.. Ответ, конечно, будет носить вероятностный характер. 7.2. Логика проверки статистической гипотезы. Использование принципа невозможности реализации маловероятных событий Приведенные в настоящем параграфе рассуждения, на наш взгляд, читателю было бы целесообразно прочитать дважды: сейчас и после прочтения дальнейших параграфов, посвященных описанию способов проверки конкретных гипотез. Для примера заметим, что качестве проверяемой статистической гипотезы в описанной выше ситуации может фигурировать гипотеза о том, что в генеральной совокупности наши средние (т.е. математические ожидания зарплат для мужчин и для женщин) равны. Проверяемая гипотеза всегда обозначается Н0 и называется нуль-гипотезой. Заметим, что далеко не для каждой интересующей социолога гипотезы математическая статистика предоставляется возможность ее проверки, не для каждой гипотезы разработана соответствующая теория. Но если упомянутая возможность существует, то соответствующая логика рассуждений, коротко говоря, сводится к следующему. Мы предполагаем, что для генеральной совокупности гипотеза верна. Изучаем выборку. Если выборочная ситуация резко отличается от того, что должно быть в генеральной совокупности при условии справедливости гипотезы, то гипотеза отвергается; если это отличие мало – гипотеза принимается (подчеркнем, что она не доказывается, а просто считается, что выборочные данные не дают оснований ее отвергнуть). Конечно, здесь возникают по крайней мере два вопроса: что значит «выборочная ситуация»? что значит «большое» или «малое» отличие выборочной ситуации от генеральной? Прежде всего вспомним термины «параметр» и «статистика» и заметим, что выборочную ситуацию мы будем описывать с помощью некоторых статистик, в то время как проверяемая гипотеза будет касаться определенных предположений о характере параметров генеральных распределений изучаемых (одномерных и многомерных) случайных величин. Предположим, что мы хотим проверить некую гипотезу Н0, для которой существует упомянутая выше теория. Последнее означает, что математическая статистика предлагает нам некоторый критерий, представляющий собой определенную статистику f - числовую функцию от наблюдаемых величин, например, рассчитанную на основе частот выборочной таблицы сопряженности : f = f (n ij). Представим себе теперь, что у нас имеется много выборок (при доказательстве используемых нами положений математической статистики предполагается, что выборок - бесконечное количество), для каждой из которых вычисляется значение функции f. Распределение таких функций в предположении что H0 верна, хорошо изучено, т.е. известно, какова вероятность попадания каждого значения в любой интервал. Грубо говоря, это означает, что для каждого полученного для конкретной выборки значения f , пользуясь соответствующей вероятностной таблицей, можно сказать, какова та вероятность, с которой мы могли на него «наткнуться». Теперь необходимо пояснить, какого типа распределения будут нас интересовать. Мы уже говорили, что речь пойдет о нормальном распределении, о распределениях «2», Стьюдента и F-распределении (распределении Фишера). «Маловероятными» для них всех являются области, лежащие в «хвостах» этих распределений. У первого распределения нас будет интересовать один «хвост» (правый), у трех других – два «хвоста» (и правый, и левый). Все названные распределения непрерывны. Значит, для них бессмысленно говорить о вероятности встречаемости точечного значения. И о вероятности «наткнуться» на конкретное значение fвыб мы можем судить по одной из двух вероятностей: P(f fвыб) (если fвыб0) или P(f fвыб) (если fвыб0). Пока будем говорить о ситуации, когда fвыб0. Все, что будет по этому сказано, потом распространим на более общую ситуацию, специально посвятив этому параграф (см. ниже обсуждение вопроса о направленных и ненаправленных альтернативных гипотезах и об односторонних и двусторонних критериях в процессе рассмотрения темы 9). Итак, вычисляем значение fвыб критерия f для нашей единственной выборки. Находим по таблице вероятность P(f fвыб). Далее вступает в силу своеобразный принцип (уже затронутый нами в п.6.1) : маловероятное событие практически не может произойти. Другими словами, принимая практическое управленческое решение, мы, узнав, что некоторое событие имеет малую вероятность, будем вести себя так, как если бы это событие не могло произойти. Если такое маловероятное событие встречается в наших теоретических рассмотрениях, то мы делаем из этого вывод, что вероятность определялась нами неправильно, что в действительности рассматриваемое событие не маловероятно и что, следовательно, мы должны пересмотреть те положения, которые привели нас к выводу о незначительности величины вероятностиь его встречаемости мала. Наше событие состоит в том, что критерий принял то или иное значение. Если вероятность этого события, (т.е. P(f fвыб)) очень мала, то, в соответствии с приведенными рассуждениями, мы полагаем, что неправильно ее определили. Встает вопрос о выяснении того, что именно привело нас к ошибке. Вспоминаем, что мы определяли упомянутую вероятность в предположении справедливости проверяемой гипотезы. Именно это предположение и заставило нас считать вероятность встреченного значения очень малой. Поскольку опыт дает основание полагать, что в действительности вероятность не столь мала, то остается опровергнуть нашу H0. Другими словами, если выборочная ситуация такова, что ее возникновение при справедливости в генеральной совокупности проверяемой гипотезы Н0 имеет очень малую вероятность, то гипотеза отвергается. Мы проанализировали выборку (вычислили статистику f) и увидели, что произошло событие, которое при условии справедливости Н0 можно считать маловероятным (статистика приняла маловероятное значение). Поскольку, в соответствии с обсуждаемым принципом, мы полагаем, что подобное событие произойти не может, то вынуждены допустить, что неверно то условие, при выполнении которого это событие маловероятно, т.е. неверна наша Н0. Другими словами, мы отвергаем нашу гипотезу. Если же вероятность P(f fвыб) достаточно велика для того, чтобы значение fвыб могло встретиться практически, то мы полагаем, что у нас нет оснований сомневаться в справедливости проверяемой гипотезы. Мы принимаем последнюю, считаем, что она справедлива для генеральной совокупности. Другими словами, если же анализируемая нами выборочная статистика приняла значение, вероятность появления которого при условии справедливости Н0 достаточно велика, то мы полагаем, что выборочная ситуация не противоречит проверяемой гипотезе. Мы эту гипотезу принимаем. Таким образом, право именоваться критерием функция f обретает в силу того, что именно величина ее значения играет определяющую роль в выборе одной из двух альтернатив: принятия гипотезы H0 или отвержения ее. Правда, здесь снова возникает субъективный момент, связанный с неясностью того, какую вероятность мы назовем малой. Где граница между «малой» и «достаточно большой» вероятностью? Эта граница должна быть равна такому значению вероятности, относительно которого мы могли бы считать, что событие с такой (или с меньшей) вероятностью практически не может случиться – «не может быть, потому что не может быть никогда». Это значение называется уровнем значимости принятия (отвержения) проверяемой гипотезы и обозначается всегда греческой буквой . Итак, если вероятность P(f fвыб) > , то мы гипотезу принимаем на уровне значимости , если P(f fвыб) - отвергаем на том же уровне значимости. Иногда используется немного другая логика проверки. Мы задаемся уровнем значимости и заранее ищем то значение критерия, обозначаемое обычно символом f крит (критическое) или f табл (табличное), для которого имеет место соотношение P(f f крит) и, вычислив fвыб, сравниваем его с f крит: если f выб f крит, то проверяемая гипотеза отвергается, если f выб f крит, то принимается. Именно этой логики мы будем придерживаться ниже. Ниже иногда будем использовать обозначение f (fкрит) в знак того, что речь идет о том табличном (критическом) значении, которое отвечает именно уровню значимости . Математическая статистика не дает нам правил определения . Помочь установить уровень значимости может только практика. Обычно полагают, что = 0,05. В основе такого выбора не лежит никакая теория. Единственное его «оправдание» состоит в том, что, как показывает практика, если при проверке гипотез пользоваться таким уровнем значимости, то решения, принимаемые на основе проверки рассматриваемой гипотезы, как правило, оправдываются. Однако, как мы увидим ниже при проверке конкретных гипотез, соответствующий уровень зачастую бывает целесообразно связывать с содержанием задачи. Он должен обусловливаться тем, насколько социально значимым может быть принятие ложной или отвержение истинной гипотезы (процесс проверки любой статистической гипотезы всегда сопряжен с тем, что мы рискуем совершить одну из упомянутых ошибок; ниже этот вопрос будет рассмотрен более подробно). Если большие затраты (материальные или духовные) связаны с отвержением гипотезы, то мы будем стремиться сделать как можно меньше, чтобы максимально уменьшить вероятность отвержения нуль-гипотезы, являющейся в действительности верной. О ситуации, когда затраты сопряжены с принятием гипотезы, и когда, следовательно, мы должны сделать так, чтобы минимизировать вероятность принятия неверной гипотезы, мы будем говорить ниже (мы имеем в виду обсуждение ошибок первого и второго рода; принятие неверной гипотезы – это ошибка второго рода; вероятность ее осуществления связана с понятием мощности критерия, о которой мы пока говорить не будем). Перейдем к рассмотрению проверки конкретной нуль-гипотезы. 7.3. Проверка гипотезы об отсутствии связи между номинальными признаками на основе критерия «Хи-квадрат». Вернемся к рассмотрению частотной эмпирической таблицы. Будем искать ответ на вопрос о существовании связи между признаками с помощью проверки статистической гипотезы об их независимости. Используя терминологию математической статистики, можно сказать, что речь пойдет о проверке нуль-гипотезы: Н0: «связь между рассматриваемыми признаками отсутствует». Функция, выступающая в качестве описанного выше статистического критерия, носит назваание «Хи-квадрат», обозначается как Х2 (Х большое греческое «Хи»; подчеркнем, что дадлее будет фигурировать малая буква с тем же названием; и надо различать понятия, стоящие за этими обозначениями, что не всегда делается в ориентированной на социолога литературе). Определяется этот критерий следующим образом: 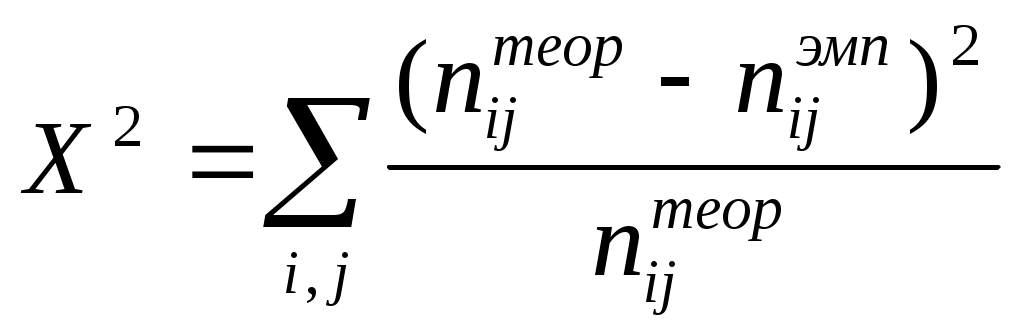 (7.2) (7.2)где В соответствии со сказанным в предыдущем параграфе, представим себе, что мы организуем (теоретически) бесконечное количество выборок, для каждой из которых вычисляем величину Х2. Образуется последовательность таких величин: Очевидно, имеет смысл говорить о соответствующем распределении, т.е. о вероятности попадания вычисленного для какой-либо выборки значения «Хи-квадрата» в тот или иной интервал. В математической статистике доказано следующее положение: если наши признаки в генеральной совокупности независимы, то величины (7.3) имеют хорошо изученное распределение, называемое «2 – распределение». С ним мы уже знакомы (здесь используется малое греческое «хи»). Приблизительность можно игнорировать (т.е. считать, что величины (7.3) в точности распределены по закону 2), если ожидаемые (теоретические) частоты достаточно велики – обычно считают, что в каждой клетке таблицы, заполненной теоретическими частотами, должно быть по крайней мере 5 наблюдений. Будем считать, что это условие соблюдено (если это не так, то какие-то значения хотя бы одного из признаков следует объединить, чтобы соответствующие строки (столбцы) таблицы сопряженности сложились и частоты вследствие этого увеличились бы (отметим, что такое укрупнение должно быть осмысленным; скажем, если мы укрупняем градации возраста, то вполне допустимо объединить интервалы (15-20) и (20-25), но вряд ли при решении какой бы то ни было задачи будет разумно соединить интервалы (15-20) и (65-70)). Вспомним, что «2 – распределение» не одно. Чтобы выделить конкретный интересующий нас вариант из соответствующего семейства распределений, необходимо задать число степеней свободы. Оно равно df = (r-1)(c-1). Чтобы логика проверки нашей нуль гипотезы стала более ясной, отметим, что при отсутствии связи в генеральной совокупности среди выборочных значений (7.3) будут преобладать значения, близкие к нулю: отсутствие связи означает близость эмпирических и теоретических частот и, следовательно, близость к нулю всех слагаемых из определения критерия Х2 (7.2). Большие значения критерия будут встречаться относительно редко и поэтому они будут маловероятны. Мы имеем только одно значение – то, которое вычислено для нашей единственной выборки. Обозначим его через Вычислим число степеней свободы df и зададимся уровнем значимости . Найдем в таблице распределения 2 такое значение ( - обозначение случайной величины, имеющей распределение2 с рассматриваемым числом степеней свободы). Если Итак, рассматриваемый критерий не гарантирует наличие связи. Не измеряет ее величину. Он либо говорит о том, что эмпирия не дает оснований сомневаться в отсутствии связи, либо, напротив, дает повод для сомнений. В заключение нельзя не сказать об очень важном (и с практической, и теоретической точки зрения) моменте: и величина критерия X2, и его расположение по отношению к табличному значению (естественно, говоря об этом, мы предполагаем, что уровень значимости зафиксирован) может измениться. Другими словами, наш вывод о наличии или отсутствии связи между переменными зависит от способа группировки значений рассматриваемых признаков. Представляется, что этот факт является интересной иллюстрацией к ведущейся в литературе дискуссии по вопросу объективности знания, получаемого социологом! 54. Отметим, что при разной группировке значений какого-либо признака мы по существу переходим к разным признакам, отражающим разные стороны реальности. Так, сгруппировав значения возраста (не учитываем детство) так: (15-20), (20-50), (50-80), мы по существу отразим физическое состояние организма человека: растущий организм, стабильный, деградирующий. А сгруппировав по-другому: (15-20), (20-30), (30-80), получим признак, отражающий степень социальной зрелости человека (мы не претендуем на содержательную правильность предлагаемых разбиений). 55 Примеры задач 1.Доказать эквивалентность соотношений (7.1). Рекомендация к дальнейшему. Если имеются клетки, которым отвечают теоретические частоты, меньшие 5, то градации признаков надо укрупнять (разумным способом). При этом надо учесть, что чем меньше укрупнений – тем лучше, поскольку мы теряем меньше информации (естественно, какждое «слияние» градаций того или иного признака приводит к потере информации). 2. Проанализировав данные по абитуриентам, поступавшим в некоторый вуз, получили следующие частоты:
Можно ли считать, что обучение на подготовительных курсах способствует более эффективной подготовке к экзамену? Рекомендация. Данная задача может решаться двумя способами. Применить оба и содержательно проинтерпретировать разницу в выводах 3. Данные опроса жителей некоторого промышленного региона об их электоральном поведении были сведены в следующую частотную таблицу (частоты в клетках выражены в десятках тысяч человек):
Можно ли считать выбор партии респондентом статистически связанным с местом его проживания? Рекомендация. Пояснить, почему один из способов, пригодных для решения предыдущей задачи, здесь неприменим. 4. При анкетном опросе жителей Татарстана (сотрудников госпредприятий) фрагмент одной из частотных таблиц имел вид:
Можно ли сказать, что в республике имеется определенная дискриминация по национальности при назначении человека на должность в государственной предприятии? Придумайте пример задачи, в которой вывод о наличии (или отсутствии) связи между двумя непрерывными признаками (при использовании критерия «Хи-квадрат») зависел бы от группировки значений признаков (уровень значимости предполагается заданным). Попробуйте объяснить этот феномен. ТЕМА 8. Проверка гипотезы о равенстве средних 8.1. Понятие зависимых и независимых выборок. Выбор критерия для проверки гипотезы Н0: 1 = 2 в первую очередь определяется тем, являются ли рассматриваемые выборки зависимыми или независимыми. Введем соответствующие определения. Опр. Выборки называются независимыми, если процедура отбора единиц в первую выборку никак не связана с процедурой отбора единиц во вторую выборку. Примером двух независимых выборок могут служить обсуждавшиеся выше выборки мужчин и женщин, работающих на одном предприятии (в одной отрасли и т.д.). Заметим, что независимость двух выборок отнюдь не означает отсутствие требования определенного рода сходства этих выборок (их однородности). Так, изучая уровень дохода мужчин и женщин, мы вряд ли допустим такую ситуацию, когда мужчины отбираются из среды московских бизнесменов, а женщины – из аборигенов Австралии. Женщины тоже должны быть москвичками и, более того – «бизнесвуменшами». Но здесь мы говорим не о зависимости выборок, а о требовании однородности изучаемой совокупности объектов, которое должно удовлетворяться и при сборе, и при анализе социологических данных56. Опр. Выборки называются зависимыми, или парными, если каждая единица одной выборки «привязывается» к определенной единице второй выборки. Последнее определение, вероятно, станет более ясным, если мы приведем пример зависимых выборок. Предположим, что мы хотим выяснить, является ли социальный статус отца в среднем ниже социального статуса сына (полагаем, что мы можем измерить эту сложную и неоднозначно понимаемую социальную характеристику человека). Представляется очевидным, что в такой ситуации целессобразно отбрать пары респондентов (отец, сын) и считать, что каждый элемент первой выборки (один из отцов) «привязан» к определенному элементу второй выборки (своему сыну). Эти две выборки и будут называться зависимыми. 8.2. Проверка гипотезы для независимых выборок Для независимых выборок выбор критерия зависит от того, знаем ли мы генеральные дисперсии 12 и 22 рассматриваемого признака для изучаемых выборок. Будем считать эту проблему решенной, полагая, что выборочные дисперсии совпадают с генеральными. В таком случае в качестве критерия выступает величина: 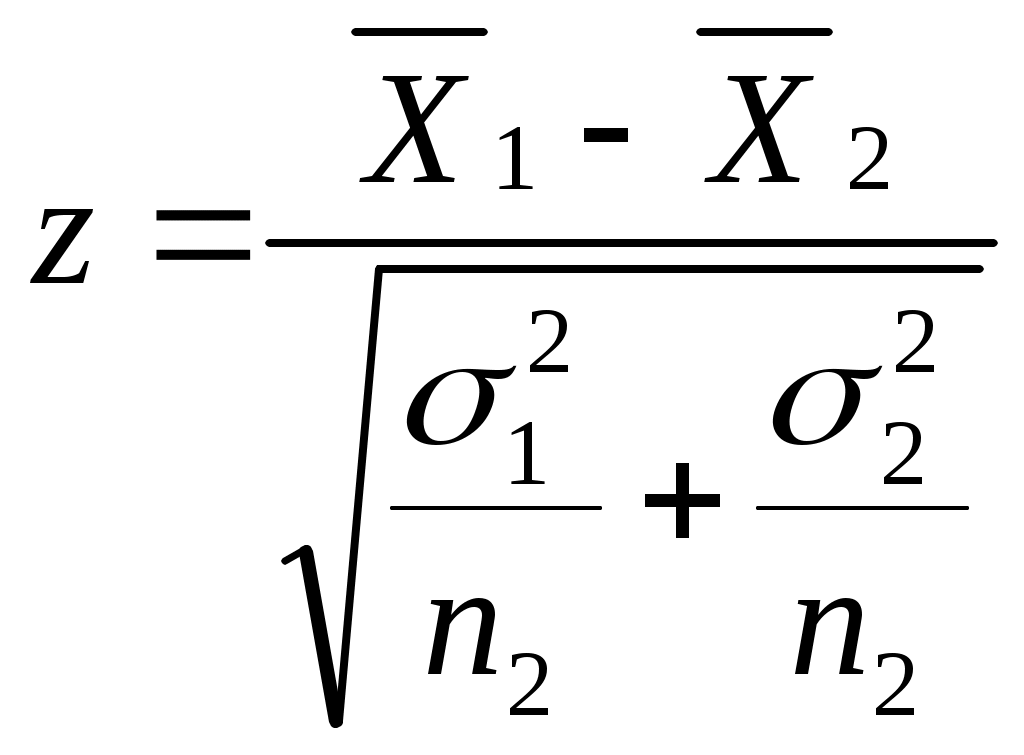 Прежде, чем переходить к обсуждению той ситуации, когда генеральные дисперсии (или хотя бы одна из них) нам неизвестны, заметим следующее. Логика использования критерия (8.1) похожа на ту, которая была описана нами при рассмотрении критерия “Хи-квадрат” (7.2). Имеется лишь одно принципиальное отличие. Говоря о смысле критерия (7.2), мы рассматривали бесконечное количество выборок объема n, «черпающихся» из нашей генеральной совокупности. Здесь же, анализируя смысл критерия (8.1), мы переходим к рассмотрению бесконечного количества пар выборок объемом n1 и n2. Для каждой пары и рассчитывается статистика вида (8.1). Совокупности получаемых значений таких статистик, в соответствии с нашими обозначениями, отвечает нормальное распределение (как мы условились, буква z используется для обозначения такого критерия, которому отвечает именно нормальное распределение). Итак, если генеральные дисперсии нам неизвестны, то мы вынуждены вместо них пользоваться их выборочными оценками s12 и s22. Однако при этом нормальное распределение должно замениться на распределение Стьюдента – z должно замениться на t (как это имело место в аналогичной ситуации при построения доверительного интервала для математического ожидания). Однако при достаточно больших объемах выборок (n1, n2 30) , как мы уже знаем, распределение Стьюдента практически совпадает с нормальным. Другими словами, при больших выборках мы можем продолжать пользоваться критерием: 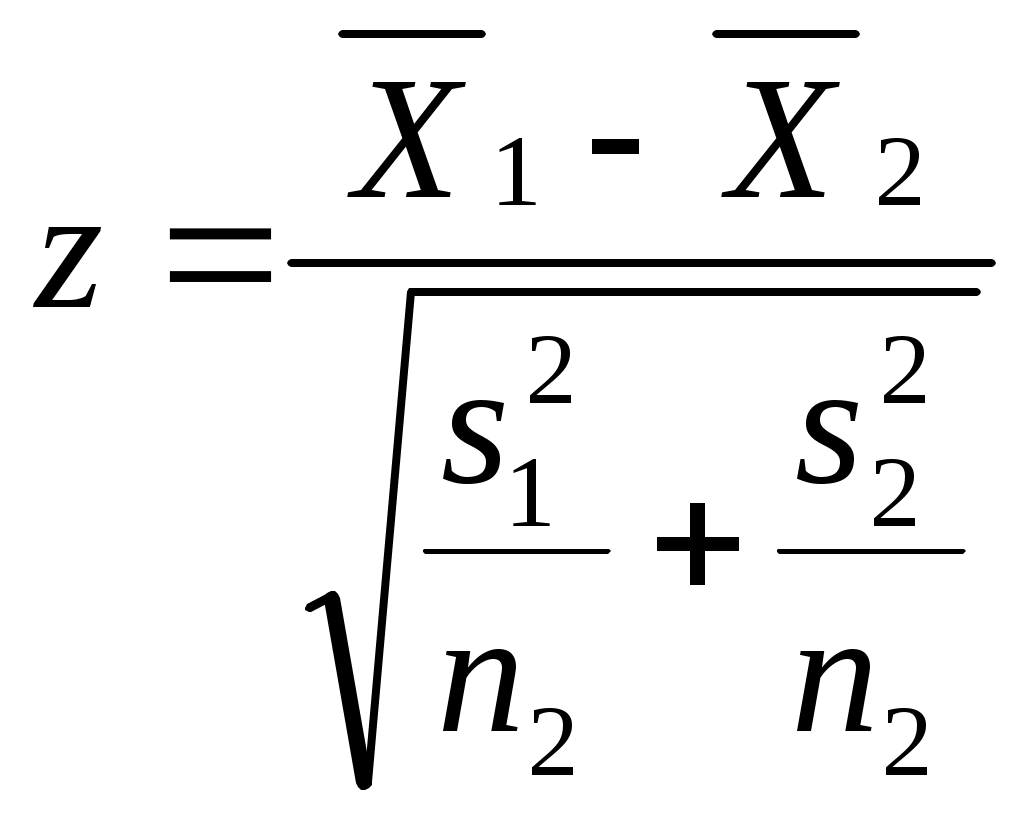 (8.2) (8.2)Сложнее обстоит дело с такой ситуацией, когда и дисперсии неизвестны, и объем хотя бы одной выборки мал. Тогда вступает в силу еще один фактор. Вид критерия зависит от того, можем ли мы считать неизвестные нам дисперсии рассматриваемого признака в двух анализируемых выборках равными. Для выяснения этого надо проверить гипотезу: H0 : 12 = 22. (8.3) Для проверки этой гипотезы используется критерий О специфике использования этого критерия пойдет речь ниже, а сейчас продолжим обсуждать алгоритм выбора критерия, использующего для проверки гипотез о равенстве математических ожиданий. Если гипотеза (8.3) отвергается, то интересующий нас критерий приобретает вид: 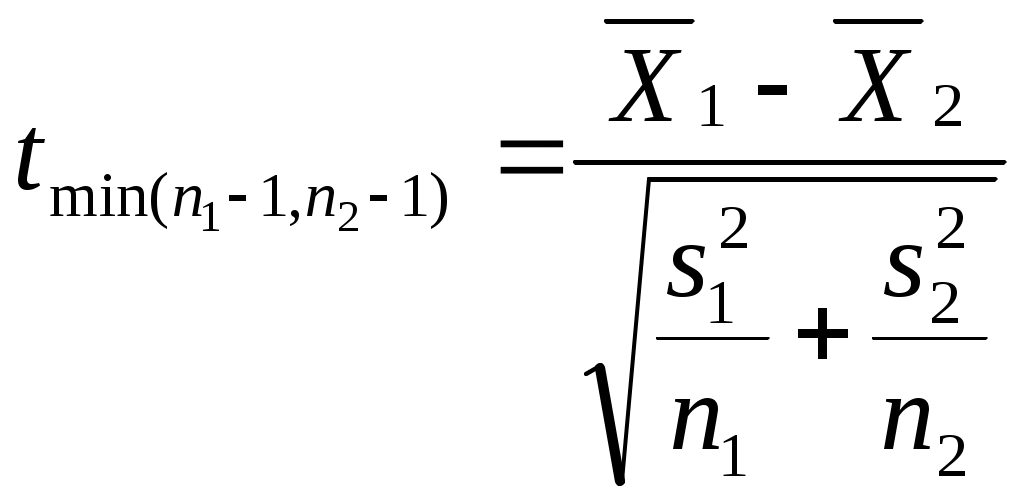 (8.5) (8.5)(т.е. отличается от критерия (8.2), использовавшегося при больших выборках, тем, что соответствующая статистика имеет не нормальное распределение, а распределение Стьюдента). Если гипотез (8.3) принимается, то вид используемого критерия меняется: 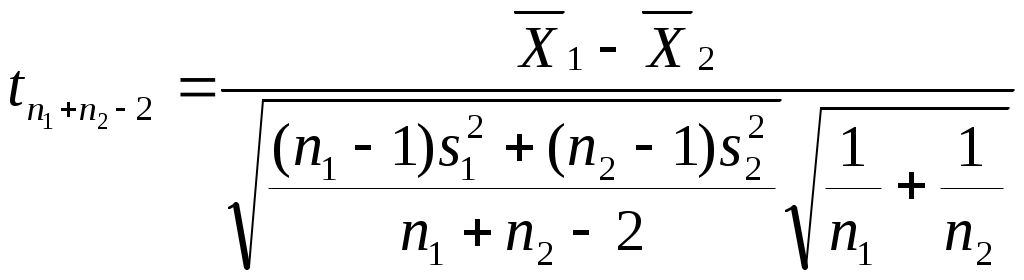 (8.6) (8.6)Подведем итог того, как выбирается критерий для проверки гипотезы о равенстве генеральных математических ожиданий на основе анализа двух независимых выборок. известны 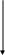 1 и 2 1 и 2  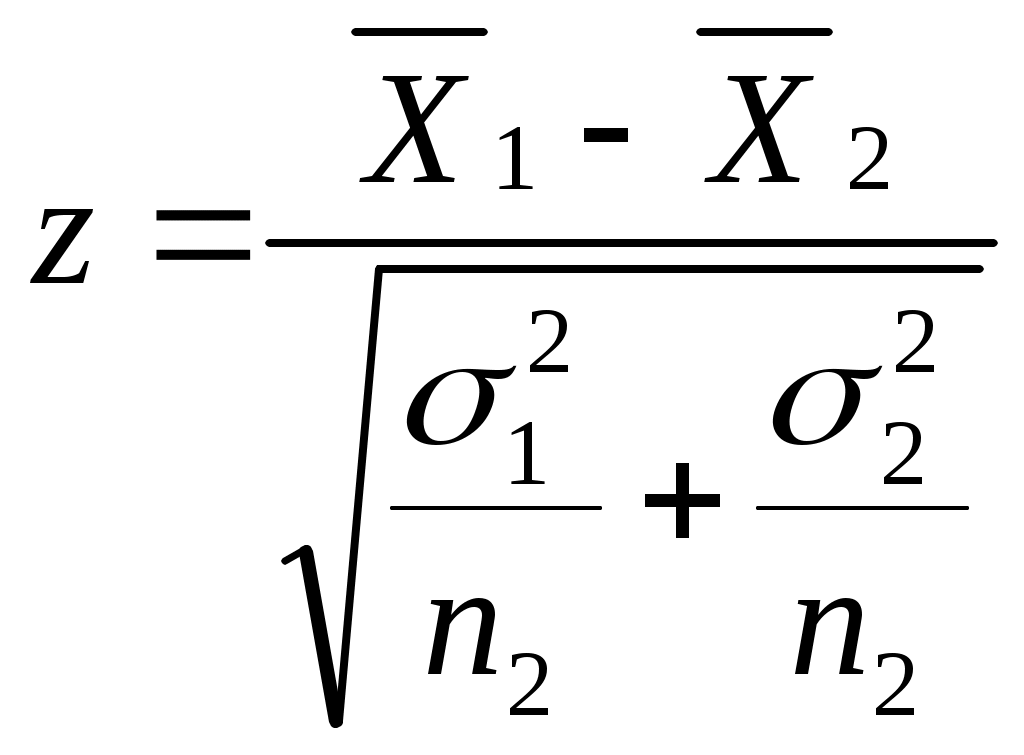 неизвестны размер выборок большой м  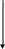 алый алый 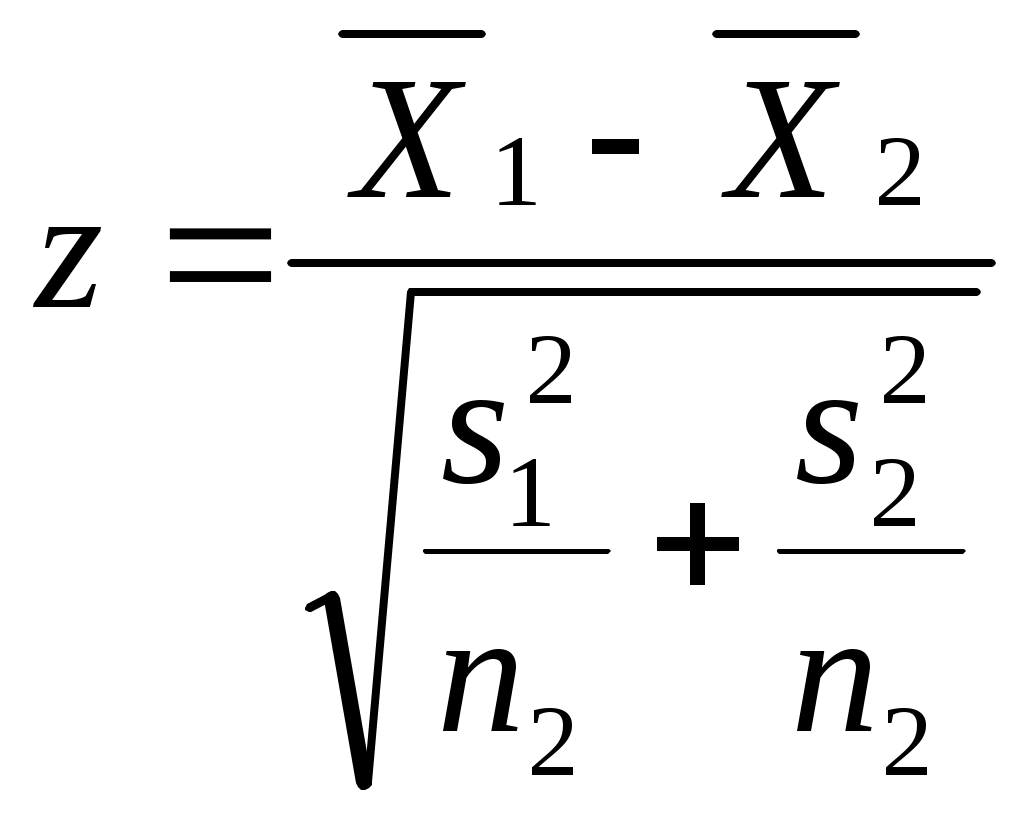 H0: 1 = 2 отвергается  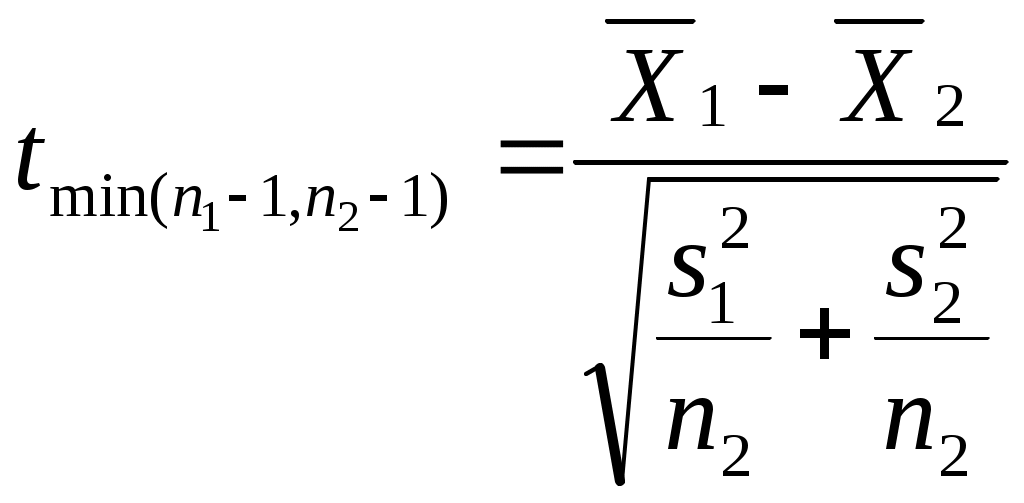 п 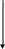 ринимается ринимается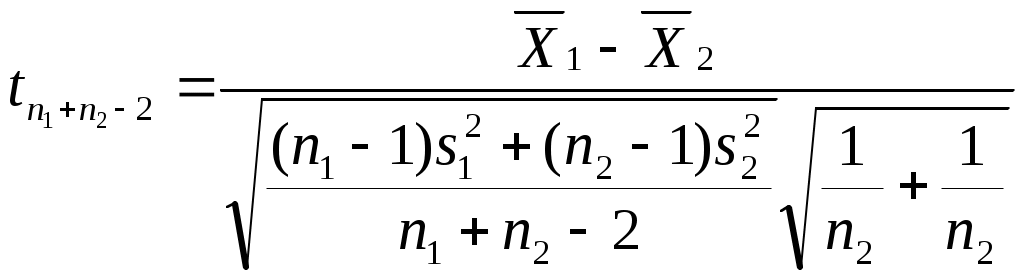 8.3. Проверка гипотезы для зависимых выборок Перейдем к рассмотрению зависимых выборок. Пусть последовательности чисел X1, X2, … , Xn ; Y1, Y2, … , Yn – это значения рассматриваемой случайной для элементов двух зависимых выборок. Введем обозначение: Di = Xi - Yi, i = 1, ... , n. Для зависимых выборок критерий, позволяющий проверять гипотезу H0: 1 = 2 выглядит следующим образом: 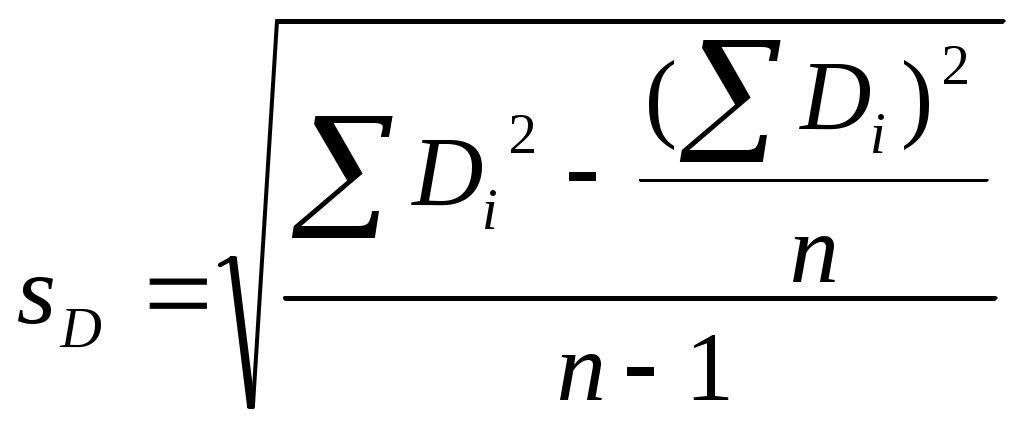 Заметим, что только что приведенное выражение для sD есть не что иное, как новое выражение для известной формулы, выражающей среднее квадратическое отклонение. В данном случае речь идет о среднем квадратическом отклонении величин Di. Подобная формула часто используется на практике как более простой (по сравнению с «лобовым» подсчетом суммы квадратов отклонений значений рассматриваемой величины от соответствующего среднего арифметического) способ расчета дисперсии. Если сравнить приведенные формулы с теми, которые мы использовали при обсуждении принципов построения доверительного интервала, нетрудно заметить, что проверка гипотезы о равенстве средних для случая зависимых выборок по существу является проверкой равенства нулю математического ожидания величин Di. Величина есть среднее квадратическое отклонение для Di. Поэтому значение только что описанного критерия tn-1 по существу равно величине Di, выраженной в долях среднего квадратического отклонения. Как мы говорили выше (при обсуждении способов построения доверительных интервалов), по такому показателю можно судить о вероятности рассматриваемого значения Di. Отличие состоит в том, что выше шла речь о простом среднем арифметическом, распределенном нормально, а здесь – о средних разностей, такие средние имеют распределение Стьюдента. Но рассуждения о взаимосвязи вероятности отклонения выборочного среднего арифметического от нуля (при математическом ожидании, равном нулю) с тем, сколько единиц это отклонение составляет, остаются в силе. Примеры задач1. Н  а основе обработки массива анкет была получена следующая частотная таблица: а основе обработки массива анкет была получена следующая частотная таблица:  Зарплата Возраст Зарплата ВозрастДо 30 лет Старше 30 лет  До 500 30 10 500-1000 20 10 1000-1500 20 15 1500-1200 10 25 Можно ли считать, что средняя зарплата молодых респондентов (моложе 30 лет) ниже средней зарплаты представителей более старшего возраста (старше 30 лет)? Пояснить статистический смысл ответа. 2. Имеем следующую статистику по регионам № региона 1 2 3 4 5 Уровень безработицы для мужчин 1,05 4,01 3,2 7,08 3,01 Уровень безработицы для женщин 1,02 5,005 3,05 2,03 3,1 Можно ли считать, что среди мужчин уровень безработицы в среднем выше? 3. В результате замеров верхнего давления респондентов были получены следующие данные:    № рес- Верхнее давление Верхнее давление пондента в спокойном состо- при прослушивании янии концерта тяжелого рока  1 120 110 2 110 130 3 100 120 4 130 130 5 110 130 Можно ли считать, что прослушивание концерта тяжелого рока в среднем повышает верхнее давление? Пояснить статистический смысл ответа. ТЕМА 9 . Направленные и ненаправленные альтернативные гипотезы. Односторонние и двусторонние критерии Теперь, когда мы познакомились с техникой проверки некоторых математико-статистических гипотез, имеет смысл коснуться очень важного момента, обусловливающего способ поиска табличного значения используемого критерия. Сделаем это прежде, чем переходить к рассмотрению других гипотез, поскольку при таком рассмотрении соответствующие положения имеет смысл активно использовать. 9.1. Направленные и ненаправленные альтернативные гипотезы. Наряду с каждой сформулированной выше нуль-гипотезой исследователь обычно формулирует и т.н. альтернативную гипотезу Н1 – то утверждение, которое он будет считать верным при отказе от H0. При рассмотрении некоторых гипотез формулировка H1 очевидна и говорить об альтернативной гипотезе не стоит. Это касается, например, той гипотезы об отсутствии связи, которую мы проверяли с помощью критерия “Хи-квадрат”. Ей противостоит единственно возможная альтернативная гипотеза, утверждающая, что связь между переменными имеется. Подобная альтернативная гипотеза называется ненаправленной. Однако не такова ситуация, возникающая при проверке статистической гипотезы о равенстве математических ожиданий. Гипотезе Н0: 1 = 2 противостоят два альтернативных утверждения: Н1: 1 2. и Н1: 1 2 (или Н1: 2 1) В первом случае альтернативная гипотеза называется ненаправленной, а во втором – направленной. В первом случае мы полагаем, что при неравенстве математических ожиданий одинаково возможны и такая ситуация, когда первое среднее больше второго, и такая, когда второе среднее больше первого. Во втором случае (когда гипотеза - направленная) считаем, что что только первое среднее может быть больше второго. Подобное предположение может объясняться либо чисто содержательными соображениями, когда вторая ситуация, не отраженная в нашей альтернативной гипотезе (второе среднее больше первого), просто не может возникнуть; либо тем, что вторая ситуация нас просто не интересует (например, нас может интересовать, имеется ли в какой-то отрасли промышленности дискриминация женщин по оплате; тогда мы будем проверять гипотезу о равенстве средних зарплат мужчин и женщин, ориентируясь на оценку вероятности того, что зарплата мужчин выше зарплаты женщин; ситуация же, когда средняя зарплата женщин выше средней зарплаты мужчин нас будет «волновать» ровно в той же мере, что и ситуация, когда указанные зарплаты равны). За каждым видом выбранной альтернативы часто стоит свое понимание ситуации проверки гипотезы. 9.2. Односторонние и двусторонние критерии Предположим, что мы проверяем гипотезу Н0: 1 = 2 и альтернативной гипотезой является гипотеза Н1: 1 2. Выбор альтернативной гипотезы означает следующее. При анализе описанной выше мысленной конструкции с бесконечным количеством пар выборок у нас могут встречаться и такие пары, для которых наш критерий (неважно, какой – (8.1), (8.2), (8.5) или (8.6)) положителен (т.е.первая средняя больше второй), и такие, для которых критерий отрицателен (вторая средняя больше первой). Соответственно, оценивая вероятность попадания конкретного выборочного значения критерия в тот или иной интервал, мы должны учитывать, что маловероятными областями являются не только правый конец оси, но и левый. Значит, маловероятная критериальная область, попадание в которую приведет нас к решению об отвержении гипотезы, распадется на две части. Уровень значимости должен будет отвечать двум концам нормального распределения (этой величине должна быть равна сумма площадей и под правым, и под левым его концом). В таблицах же, как правило, указывается только такое табличное значение, которое отвечает правому концу. Чтобы это учесть, надо будет искать zкрит, отвечающее величине /2. И если наше zвыб окажется отрицательным, то мы будем его сравнивать со значением (- zкрит). Другими словами, мы будем принимать проверяемую гипотезу, если и отвергать ее, если Совершенно аналогичные рассуждения справедливы и для того случая, когда используемый критерий имеет распределение Стьюдента. Соответствующие статистики тоже могут быть положительными и отрицательными, а распределение очень похоже на нормальное – тоже представляет собой симметричный «колокол». При распределении F рассуждение несколько меняется. Соответствующие критерии всегда положительны (как мы увидим ниже, они «строятся» из дисперсий – статистик, не могущих принимать отрицательные значения). Тем не менее, они могут быть двусторонними. По таблице мы ищем Fкрит для правого конца распределения. Отвечать оно должно, как и выше, величине /2. А табличное значение для левого конца будет равно (1/ Fкрит). И проверяемая гипотеза принимается, если и отвергается, если Fвыб Fкрит или Fвыб Для критерия «Хи-квадрат» (и для других статистик, имеющих распределение 2) альтернативная гипотеза не направлена, но критерий всегда односторонен. Как мы увидим ниже, не так обстоит дело с другим показателем связи - коэффициентом корреляции, поскольку он, как известно, может быть и положительным, и отрицательным. Соответствующий критерий (а речь пойдет о распределении Стьюдента) может и односторонним, и двусторонним. ТЕМА 10 Проверка статистических гипотез: о равномерности генерального распределения, о равенстве дисперсий, о равенстве нулю коэффициента корреляции, о равенстве двух долей; ошибки первого и второго рода. . 10.1. Проверка гипотезы о равномерности генерального распределения с помощью критерия Хи-квадрат В социологических исследованиях нередко возникают ситуации, когда социологу надо знать, можно ли имеющееся у него частотное распределение, отвечающее какому-либо признаку, считать выборочным представлением распределения определенного характера: нормального, равномерного и т.д. Так, многие математические методы требуют (если мы хотим, чтобы применение метода было корректным), чтобы распределение каждого из исходных признаков было нормальным. Выборочное частотное распределение может в какой-то степени походить на нормальное: скажем, быть одновершинным, в како-то степени симметричным и т.д.Можем ли мы считать, что в генеральной совокупности оно нормально? Что его отклонение от нормальности можно объяснить только случайными погрешностями выборки? Ясно, что подобная ситуация очень похожа на те описанные выше ситуации, когда мы отвевчали на вопросы, подобные только что сформулированным, с помощью проверки статистической гипотезы. Оказывается, что и здесь таким же образом можно найти ответ: математическая статистики предлагает нам соответствующий механизм. Существует критерий, позволяющий проверять гипотезу о том, что распределение имеет определенный характер57. Это уже знакомый нам критерий «Хи-квадрат». В общем виде он имеет вид: где O – эмпирические, наблюдаемые, фактические частоты, E– теоретические, ожидаемые частоты. Теоретические частоты – это те, которые мы видели бы (ожидали) в случае, если бы распределение имело характер, отвечающий проверяемой гипотезе. Поясним сказанное на примере проверки гипотезы о равномерности генерального распределения. Пусть рассматриваемый признак принимает значения 1,2, … , k, а фактически наблюдаемые (выборочные) частоты встречаемости этих значений равны, соответственно, n1эмп, n2 эмп, … , nkэмп. Отвечающие им теоретические частоты будут выглядеть так: n1теор = n2 теор = … = nkтеор = Интересующий нас критерий имеет вид: 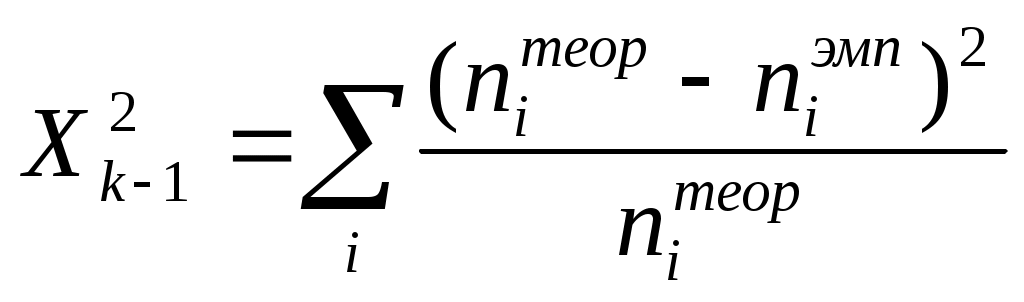 Другими словами, отличие критерия, позволяющего нам проверить гипотезу о том. что генеральное распределение является равномерным, от того критерия Хи-квадрат, который выше мы использовали для проверки гипотезы об отсутствии связи, состоит в следующем: вместо nijэмп фигурирует niэмп – фактическая частота встречаемости i-го значения рассматриваемого признака; вместо nijтеор выступает niтеор – та частота, которая должна была бы соответствовать значению i рассматриваемого признака, если бы он имел проверяемое распределение; число степеней свободы равно не (c-1)(r-1), а (k – 1), где k – количество альтернатив в рассматриваемом признаке. | ||||||||||||||||||||||||||||||||||||||||||
