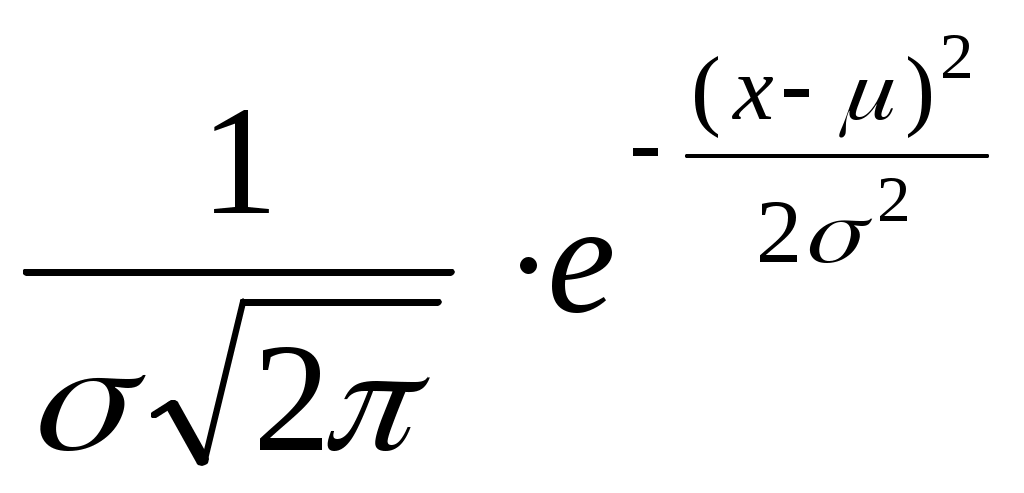Математико-статист модели в социологии. Учебное пособие оглавление введение. В основная цель курса, адресат
 Скачать 2.75 Mb.
|
N (x,
N(0,1); все необходимые сведения для случайной величины с произвольным распределением N(,) из нее могут быть получены.
N (0,1), если осуществить преобразованиеТЕМА 3Стандартизация значений случайных величин. Виды некоторых специфических распределений22, использующихся при переносе результатов с выборки на генеральную совокупность 3.1. Стандартизация (нормировка) значений случайной величины: способы и цели В эмпирических исследованиях зачастую бывают задействованы такие признаки, значения которых не сравнимы друг с другом по величине. И если мы не обратим на это внимания, то при анализе данных можем придти к нелепости. Например, предположим, что мы хотим построить типологию какой-то совокупности людей, описываемых, в частности, значениями их зарплаты и возраста. Включаем компьютер, «просим» его осуществить классификацию наших респондентов. Компьютер умеет работать с числами. В соответствии с большинством известных алгоритмов классификации, оценивая по определенным правилам степень близости между всевозможными парами объектов, программа будет близкие объекты относить к одному классу, далекие – к разным. Представим себе две пары людей: респонденты первой пары отличаются друг от друга только тем, что у одного – зарплата на 50 рублей больше, чем у другого; объекты же второй пары – только тем, что у них такая же разница в возрасте (50 лет). Вероятно, при любом разумном алгоритме, если уж первые два респондента окажутся включенными в один класс, то и вторые – тоже, и обратно. Вряд ли это можно считать разумным: какова бы ни была решающаяся задача, различие зарплаты в 50 рублей вряд ли стоит принимать во внимание, а различие в возрасте в 50 лет – напротив, по-видимому, надо будет учесть. Могут возникнуть недоразумения и из-за того, что наблюдаемые значения рассматриваемых признаков будут «колебаться» вокруг сильно отличающихся друг от друга точек числовой прямой (если, например, среднее арифметическое значение одного признака равно 5000 (рублей), а другого – 50 (лет)). Чтобы подобных недоразумений не происходило, признаки обычно определенным образом нормируют (хотя, вообще говоря, бывают задачи, когда этого делать не надо). Нормировка бывает разной. Чаще всего делают так, чтобы среднее значение признака стало равным нулю, а остальные значения измерялись в «сигмах». Нетрудно видеть, что к такой ситуации приводит следующая нормировка (стандартизация) всех значений признака x: х  3.2. Нормальное распределение (повторение). Если некоторая случайная величина имеет нормальное распределение, то будем использовать для обозначения этого обстоятельства выражение: |
х
(мы получили тем самым стандартизованное распределение).
О роли такого представления нормально распределенной случайной величины вы слышали в курсе теории вероятностей.
Для хорошего восприятия дальнейшего материала важно вспомнить, что для нормального распределения хорошо изучено, какова вероятность попадания значения соответствующей случайной величины в разные отрезки числовой оси (подробнее о том, что из курса теории вероятности следует повторить, см. в конце настоящей лекции)
3.3. Распределение Хи-квадрат
Пусть случайные величины 1, 2, ... , n - независимы и каждая имеет стандартное нормальное распределение N (0,1). Говорят, что случайная величина n 2 , определенная как
n2 = 12 + 22, ... , n2
имеет распределение хи-квадрат с n степенями свободы23. Для этой случайной величины составлены разнообразные таблицы. Чаще всего они содержат значения р-квантилей.
Заметим, что плотность распределения этой функции можно выразить определенной формулой (как мы выражали, например, плотность функции нормального распределения). Но эта формула очень сложна, поэтому мы не выписываем ее в основной части текста24.
.
Подчеркнем, что существует не одно распределение хи-квадрат, а целое семейство таких распределений, каждый член семейства задан отвечающим ему значением n. Другими словами, для каждого n существует свое распределение хи-квадрат. И если нам понадобится таблица, задающая это распределение, то мы должны будем выбрать нужную из целого семейства таблиц, каждая из которых задается своим числом степеней свободы.
Далее мы увидим, что понятие числа степеней свободы имеет смысл и для других распределений. Часто число степеней свободы рассматриваемого распределения обозначают сочетанием букв df (degree of freedom).
Известно, что Мn2 = n, Dn2 = 2n, Mo n2 = n – 2 (для n 2).
Для сравнения напомним, что нормальное распределение тоже задается парой двух параметров – математическим ожиданием и дисперсией; однако чтобы связать какое-либо значение нормально распределенной случайной величины
Приведем графики плотности распределения 22 и 32 (см. рис. 3.2).
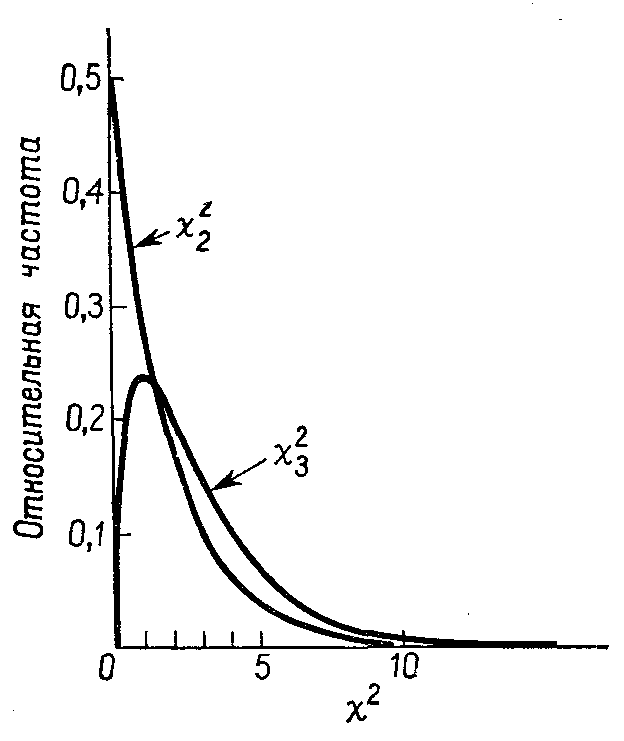
Рис. 3.2. Функции плотности распределения «Хи-квадрат» с числом степеней свободы 2 и 3.25
(вдоль вертикальной оси, строго говоря, следовало бы написать «плотность вероятности», а не «относительная частота»; второе, вообще говоря, годится лишь при работе с выборкой) !!!!!!!!!!!!!!!!!!!!!
Приведем примеры «Хи-квадрат»-распределений с другими числами степеней свободы, указывая при этом, вероятности попадания значений рассматриваемых случайных величин в некоторые полуинтервалы.
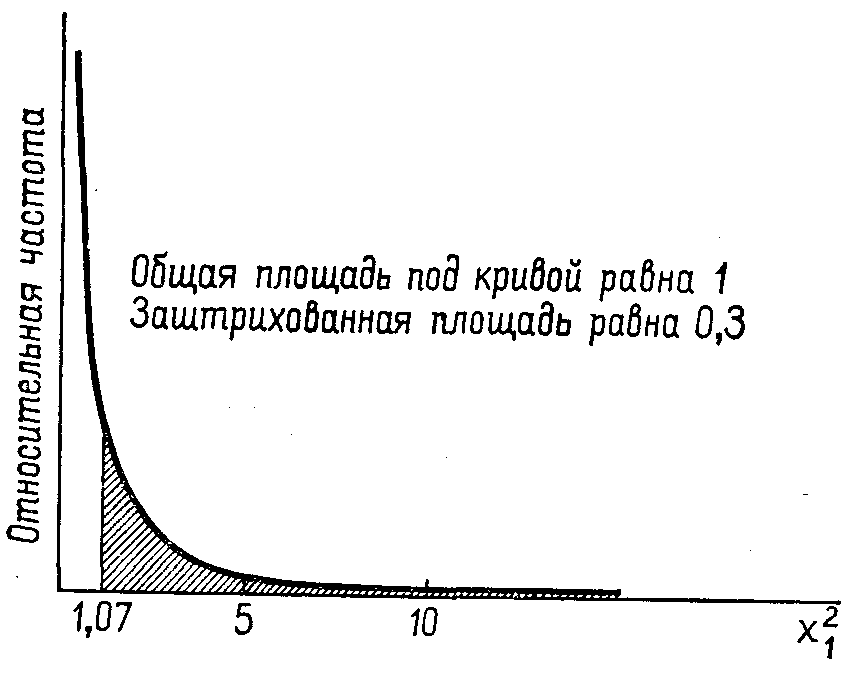
Рис. 3.3. Функция плотности распределения «Хи-квадрат» с числом степеней свободы 1. 26
(вдоль вертикальной оси, строго говоря, следовало бы написать «плотность вероятности», а не «относительная частота»; второе, вообще говоря, годится лишь при работе с выборкой) !!!!!!!!!!!!!!!!!!!!!!!!!
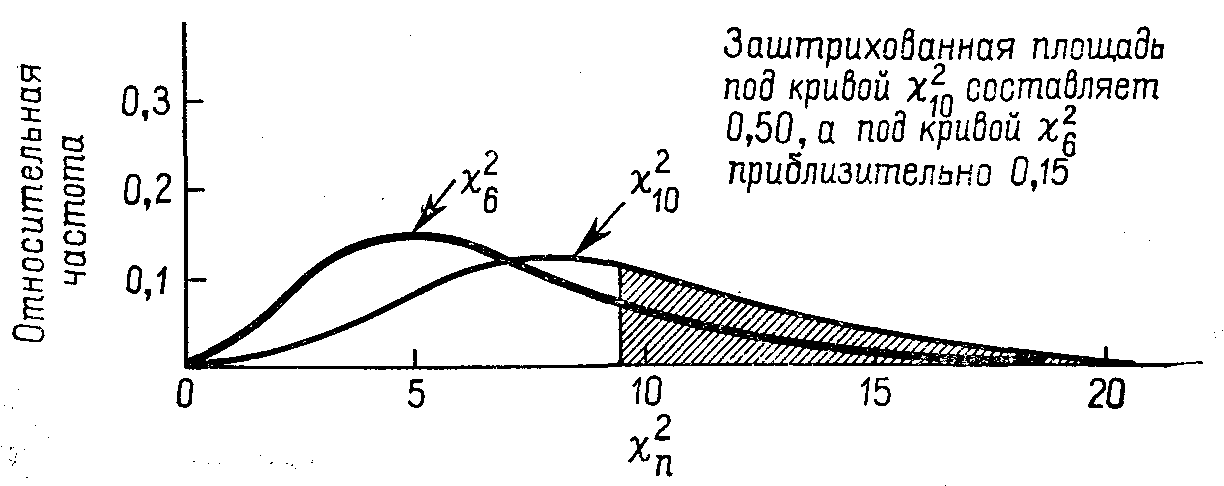
Рис. 3.4. Функции плотности распределения «Хи-квадрат» с числом степеней свободы 6 и 10.27
(вдоль вертикальной оси, строго говоря, следовало бы написать «плотность вероятности», а не «относительная частота»; второе, вообще говоря, годится лишь при работе с выборкой) !!!!!!!!!!!!!!!!!!!!!
3.4.Распределение Стьюдента28 (t-распределение)
Пусть случайные величины 0, 1, ... , n – независимы и каждая имеет стандартное нормальное распределение N(0,1)29. Говорят, что случайная величина tn, определенная как
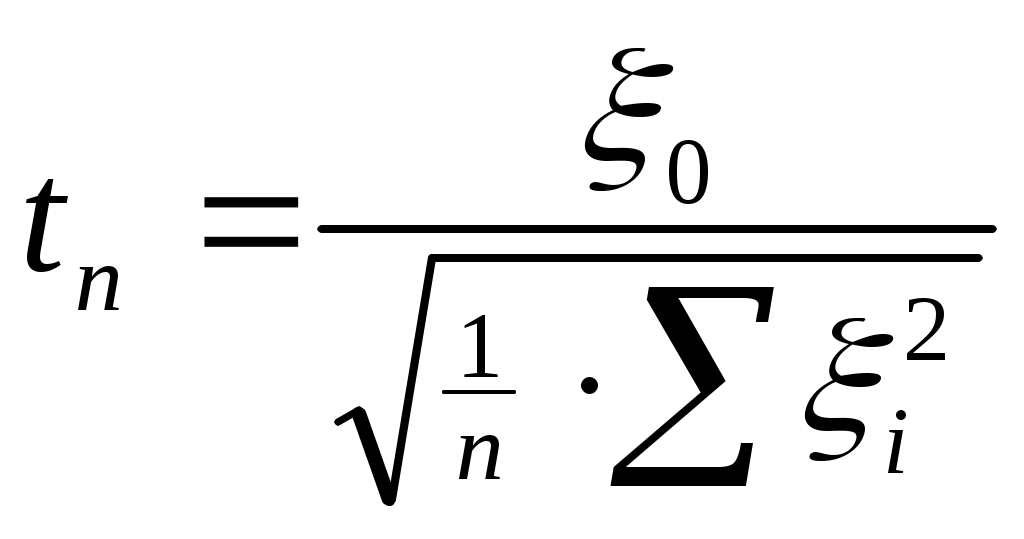
имеет распределение Стьюдента с n степенями свободы.
M t n = 0; D t n = n / (n – 2) (n 2); Mo = 0.
При больших n вместо распределения Стьюдента обычно рекомендуется использовать стандартное нормальное распределение. Встает вопрос о том, какие выборки называть большими. В западной традиции большой называют выборку, если n 30 (см., например, учебник Блумана). Отечественная наука более осторожна: большой называется выборка, если n 100. Строгих правил здесь не может существовать в принципе. Все зависит от того, какая степень надежности получаемых выводов нам требуется. Ответ на вопрос об объеме выборки может дать только практика. При этом российские ученые опираются на практику использования математической статистики в естественных науках и технике, а западные учитывают и опыт гуманитарных наук, где погоня за большой точностью и надежностью зачастую теряет смысл, поскольку достаточно «грубыми» являются результаты измерений рассматриваемых признаков (социолога обычно волнует вопрос о том, то ли он меряет, что хочет, и вопрос о точности уходит на второй план). Так что мы далее будем считать, что выборки объема более 30 – достаточно большие для того, чтобы распределение Стьюдента подменять нормальным.
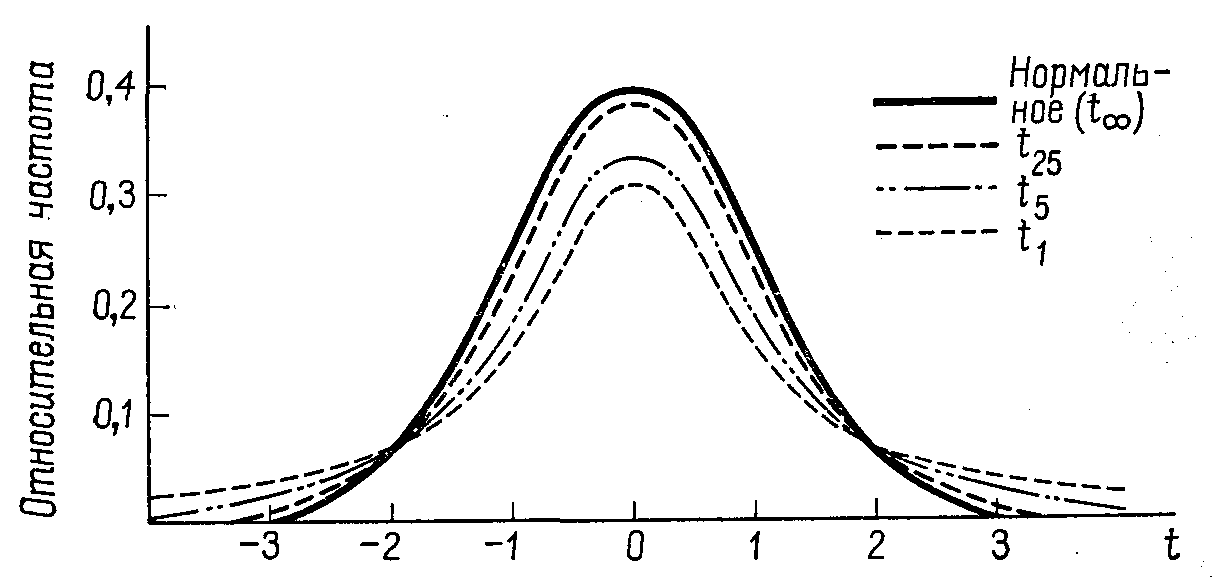
Рис. 3.5. Функции плотности распределения Стьюдента с различным числом степеней свободы. Для сравнение на том же графике приведена функция плотности нормального распределения. 30
КРАСНОЕ – МЕЛКИМ ШРИФТОМ
И еще один вопрос должен был бы возникнуть у читателя (правда, за 10 лет чтения автором лекций по рассматриваемому предмету студентам-социологам нашелся лишь один слушатель, задавший этот вопрос): что делать, если n=1 или n=2? Дисперсия будет отрицательной? Нам представляется полезным дать ответ на этот вопрос, поскольку этот ответ позволит читателю-социологу вспомнить кое-что из интегрального исчисления и лишний раз убедиться в том, что полученные им на первом курсе вуза знания по высшей математике отнюдь не бесполезны.
Ответ на указанный вопрос таков: при n=1 или n=2 дисперсия соответствующего распределения Стьюдента не существует. ДАЛЕЕ, до п. 3.5, - МЕЛКИМ ШРИФТОМ.
Позволим себе привести здесь доказательство этого факта для n=1 (что, на наш взгляд, должно иметь определенное «воспитательное» значение).
Плотность распределения Стьюдента имеет вид:
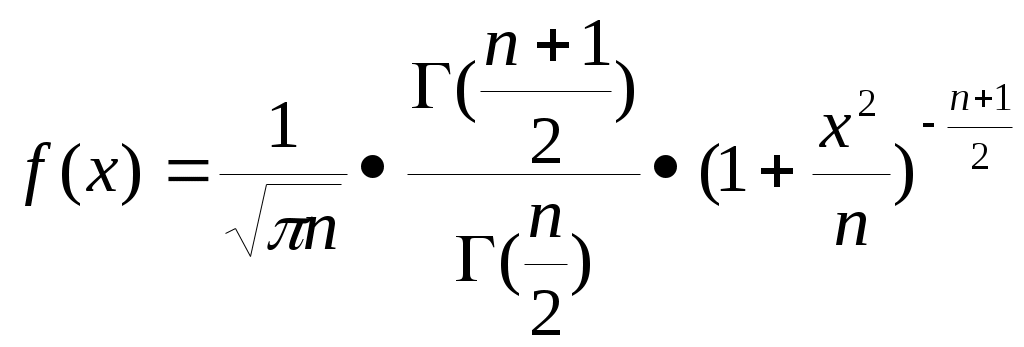
(- х +, напомним, что т.н. гамма-функция имеет вид: Г(z ) =
). При n=1 f (x) принимает вид: 
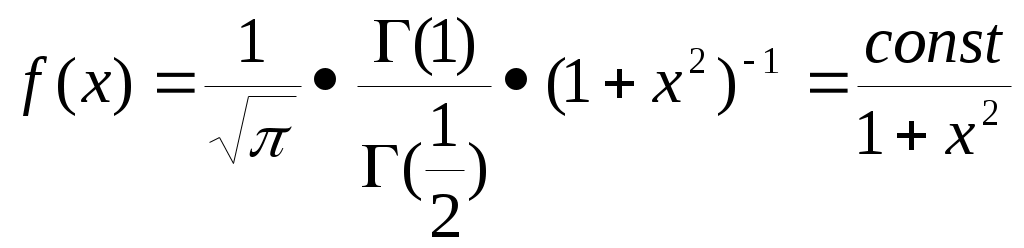
где const – это некоторая величина, не зависящая от нашей переменной x.
Напомним, что: (1) дисперсия случайной величины х равна D(x) = M (x - M(x))2 , (2) математическое ожидание случайной величины x с плотностью распределения f(x) вычисляется по формуле: M (x) =
, (3) математическое ожидание величины, распределенной по закону Стьюдента, равно нулю. Поэтому для рассматриваемого нами случая имеет место цепочка равенств:D(x) = M (x2) =
= const
= (x – arctg x) |+- = - - = -Другими словами, интеграл расходится, т.е. интересующая нас дисперсия не существует
Распределение Фишера31(F – распределение, распределение дисперсионного отношения).
Пусть случайные величины 1, 2 .m; 1, 2, ..., n (m и n – натуральные числа) – независимы и каждая имеет стандартное нормальное распределение N(0,1). Говорят, что случайная величина Fm, n, определенная как
Fm, n =
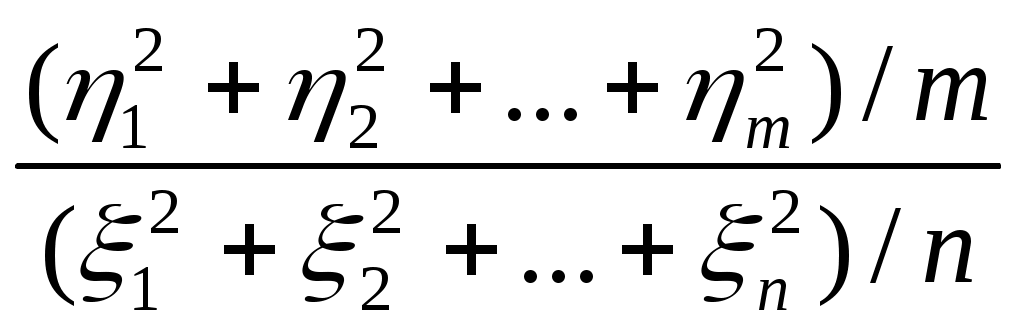,имеет F-распределение с параметрами m и n. Натуральные числа m и n называют числами степеней свободы.
М F m, n = n / (n – 2) для n 2, D F m, n = (2 n2(m + n – 2)) / (m ( n – 2) 2(n –4)) для n 4
; Mo = n (m– 2) / m (n + 2), m 1.
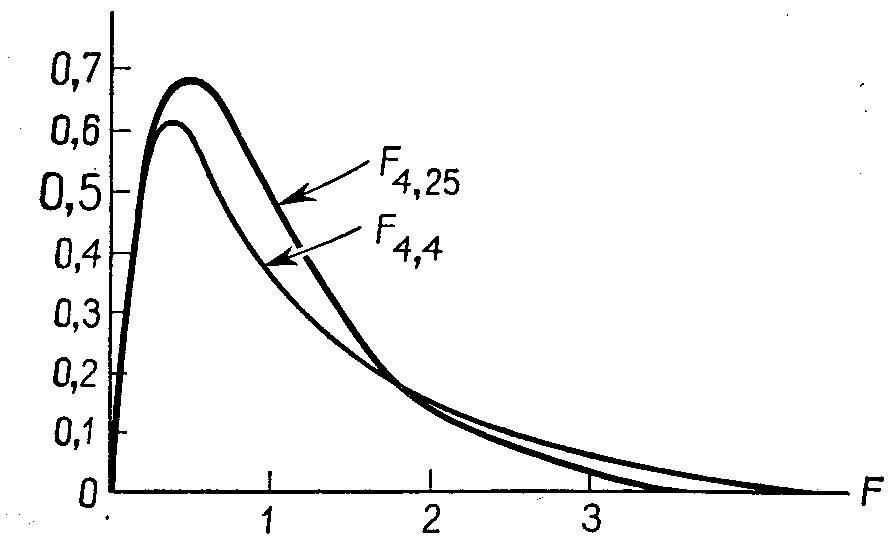
Рис. 3.6. Функции плотности F-распределения с разным числом степеней свободы32
Повторение отдельных фрагментов курса по теории вероятностей
Общее представление о вероятностных таблицах. Принципы их использования.
Определение нормального распределения. Вид нормальной кривой, «физический» смысл отвечающих ей математического ожидания и дисперсии. Целесообразность измерения значения случайной величины в единицах (среднего квадратического отклонения). Соотношение площадей под нормальной кривой и вероятностей попадания в отрезки ( , 2, 3 ). Определение размера отрезка (в единицах сигма) при заданной доле попадания в него. Функция Лапласа.
Следует запомнить, каковы доли площадей под разными частями нормальной кривой; учесть, что целому числу обычно отвечают «корявые» проценты: одна – 68,3 % площади, 2 – 95,4%; а «круглые» процентам отвечает «корявое» число «сигм»: 90% - 1,64 , 95% - 1,96 , 99% - 2, 57 и т.д. Эти и другие значения представлены на рис. 3.7.
Необходимо также понимать связь функции плотности распределения с функцией распределения и принципы нахождения квантилей распредлеления (например, процентилей). Этому также может способствовать рис. 3.7, на котором отражено, как из функции плотности получается функция распределения (отвечающая накопленным процентам) и как по функции распределения можно рассчитывать процентили.
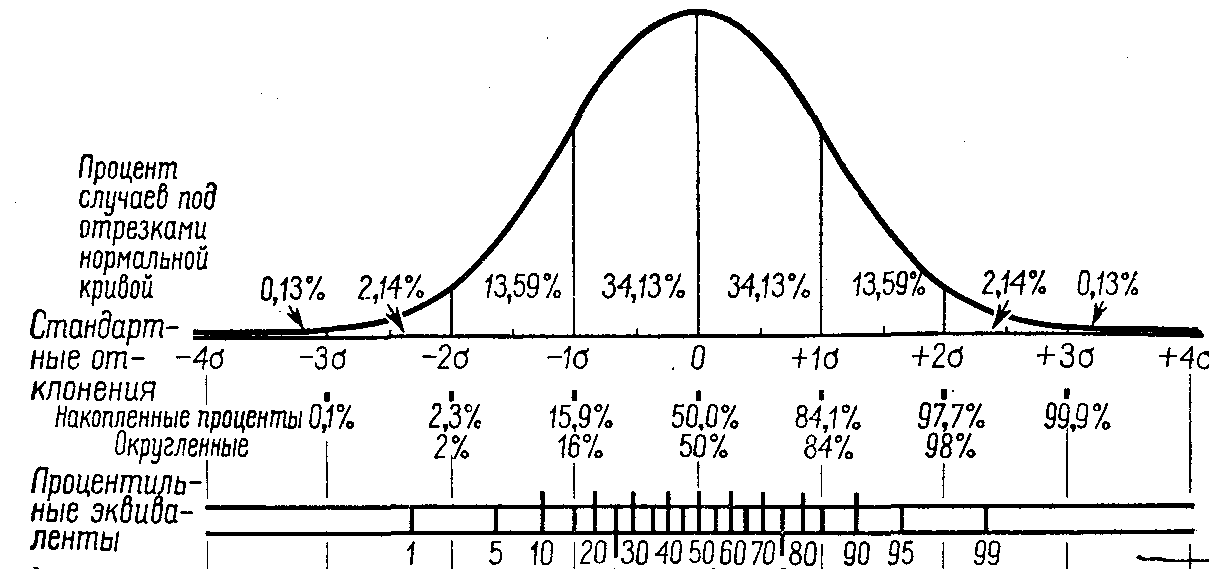
Рис. 3.7. Доли площадей под разными частями кривой плотности нормального распределения. Указание процентилей 33
(подобные иллюстрации можно найти и в других работах34).
Правило трех сигм.
Роль стандартизации нормально распределенных случайных величин при использовании соответствующих вероятностных таблиц. Использование таблицы для стандартизованной величины при получении характеристик распределения произвольной нормально распределенной случайной величины.
Пример того, как по величине отрезка под стандартизованной нормальной кривой можно определять вероятность попадания в этот отрезок соответствующей случайной величины, можно найти на рис. 3.8.
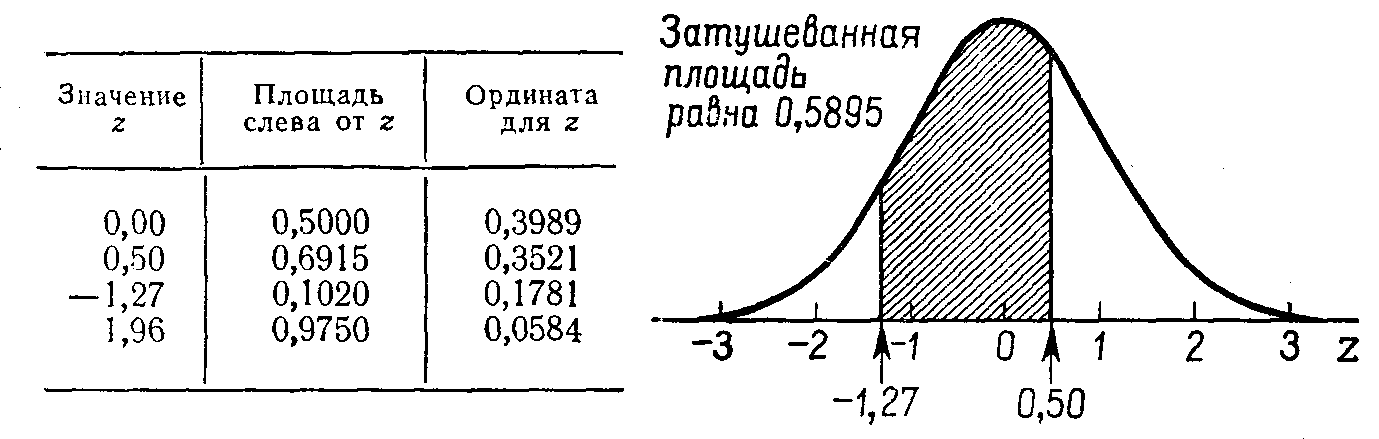
Рис. 3.8. Иллюстрация того, как отрезок диапазона изменения стандартизованной нормальной кривой связан с отвечающей этому отрезку площадью под этой кривой (т.е. с вероятностью попадания значения величины в рассматриваемый отрезок).35
Умение использовать вероятностные таблицы разного вида для нормального распределения. Желательно потренироваться на таблицах разных видов, например:
таблицы значений функции Лапласа Ф(х)36;
таблицы, в которой задана вероятность попадания в правый конец графика функции плотности (по заданному z определяется вероятность того, что f(x) > z)37;
таблицы значений удвоенной функции Лапласа38;
таблицы верхних процентных точек стандартного нормального распределения39.
Таблицы, составленные для всех остальных рассмотренных выше распределений. Их разные виды. Квантили распределений. Понимание того, что таблицы, как правило, содержат значения р-квантилей. Принцип практической невозможности маловероятных событий
Примеры задач
Доказать, что среднее арифметическое значение стандартизованного признака равно нулю, а среднее квадратическое отклонение – единице.
Известно, что распределение оценок, полученных абитуриентами при ответе на некоторый 20-балльный тест, имеет вид N (10, 3). Какова вероятность того, что абитуриент получит балл от 7 до 11? Объяснить, как находится подобная вероятность при использовании четырех видов вероятностных таблиц.
С какой площадью под графиком функции плотности стандартизованного нормального распределения соотносится значение функции Лапласа?
Как следует понимать упомянутое выше выражение «верхние процентные точки» из книги Тюрина и Макарова? В некоторых работах эти точки называются процентилями. Что такое процентиль? Что такое квантиль (частным случаем которого является процентиль)? Какие еще виды квантилей вы знаете?
ТЕМА 4
Предельные теоремы.40
При изучении результатов наблюдений над реальными массовыми случайными явлениями (над выборочными значениями изучаемых случайных величин) часто наблюдаются определенные закономерности, обладающие свойством устойчивости при рассмотрении разных выборок. Суть устойчивости состоит в том, что конкретные свойства каждого явления почти не сказываются на среднем результате. Наблюдаемые на выборке характеристики случайных величин при неограниченном увеличении количества и объема выборок становятся практически не случайными. Предельные теоремы, о которых идет речь ниже, фактически устанавливают зависимость между случайностью и необходимостью. По смыслу эти теоремы можно разбить на две большие группы – центральную предельную теорему и закон больших чисел (хотя по сути они отражают одно и то же).
4.1. Центральная предельная теорема
Центральной предельной теоремой обычно называют группу утверждений (точнее, каждое утверждение из этой группы), которые устанавливают связь между законом распределения суммы случайных величин и его предельной формой - нормальным законом распределения. Различные формулировки отличаются условиями, которые накладываются на исходные случайные величины.
Прежде всего напомним формулировку (в упрощенном виде41) одной из известных теорем А.М.Ляпунова (1857–1918) (впервые, но в более простом виде, эта теорема была доказана П.Л. Чебышевым (1821–1894) в 1887 году).
Теорема Ляпунова (1901).
Распределение суммы независимых случайных величин Х1, Х2, Х 3, ..., Хn приближается к нормальному закону распределения при неограниченном увеличении n, если выполняются следующие условия:
все величины имеют конечные математические ожидания и дисперсии;
ни одна из величин по своему значению резко не отличается от всех остальных, т.е. оказывает ничтожное влияние на их сумму.
Таким образом, предельное распределение суммы случайных величин в условиях рассмотренной теоремы не зависит от вида распределений самих случайных величин.
На опыте установлено, что распределение суммы независимых случайных величин, у которых дисперсии не отличаются резко друг от друга, довольно быстро приближаются к нормальному. Уже при числе слагаемых, большем 10, распределение суммы можно заменить нормальным.
Теорема Ляпунова справедлива и для дискретных случайных величин.
Отметим, что центральная предельная теорема имеем большое значение для социолога, поскольку она объясняет причину большого распространения в природе (в том числе – в обществе) нормального распределения, оправдывает делаемые зачастую априори, без проверки, предположения о нормальности тех распределений, которые анализируются в социологических исследованиях. Приведем пример.
В ряде методов шкалирования предполагается, что мнение человека о любом объекте плюралистично. Это означает, что если бы у нас имелся инструмент измерения такого мнения, и мы имели бы возможность использовать его много раз, то, вообще говоря, каждый раз получали бы разные значения. Этим значениям отвечало бы некоторое распределение вероятностей. Важное для нас утверждение состоит в том, что при этом обычно полагают, что указанное распределение нормально (это делается, например, в методе парных сравнений – одном из известных способов получения экспертных оценок42). И такую посылку вполне можно принять, если опереться на центральную предельную теорему.
Другая формулировка теоремы Ляпунова.
Если случайная величина Х имеет математическое ожидание МХ и дисперсию DX, то распределение среднего арифметического
= ( Хi ) / n, вычисленного по наблюдавшимся значениям случайной величины в n независимых испытаниях, проведенных в одинаковых условиях, при n 
приближается к нормальному с математическим ожиданием МХ и дисперсией DX / n. Другими словами, 
)
). (4.1)
