|
|
Математико-статист модели в социологии. Учебное пособие оглавление введение. В основная цель курса, адресат
Понятие доверительного интервала и принципы его построения (на примере математического ожидания)
Рассмотрим какой-нибудь параметр распределения изучаемой случайной величины, например, математическое ожидание, и попытаемся понять, каким образом можно судить о его значении на основе знания соответствующей выборочной точечной оценки, т.е. найденного для выборки среднего арифметического рассматриваемого признака.
Зададимся некоторой вероятностью (обычно = 0,05; подробнее об этой величине будет сказано ниже). Можно утверждать, что существует такое , для которого имеет место соотношение:
Р (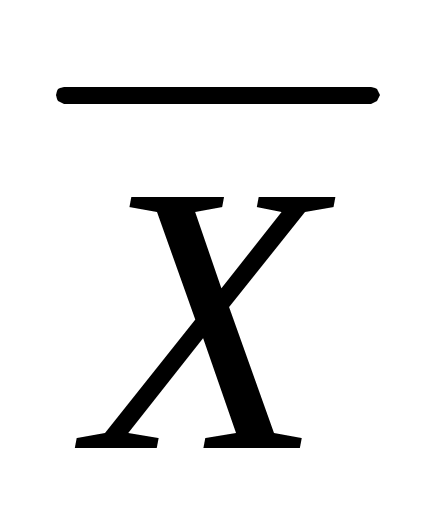 - х - х 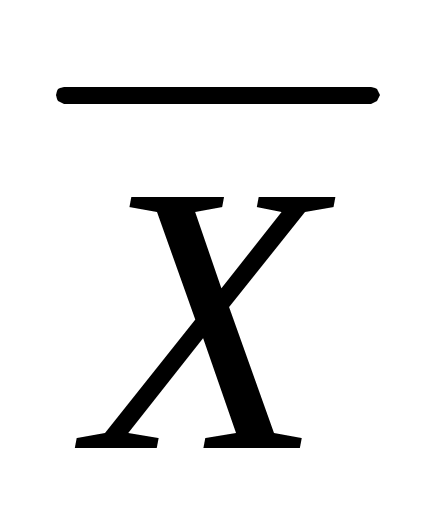 +) = 1 - , (6.1) +) = 1 - , (6.1)
Интервал вида (1) называется доверительным.
Чтобы понять, как находится , напомним, что среднее арифметическое 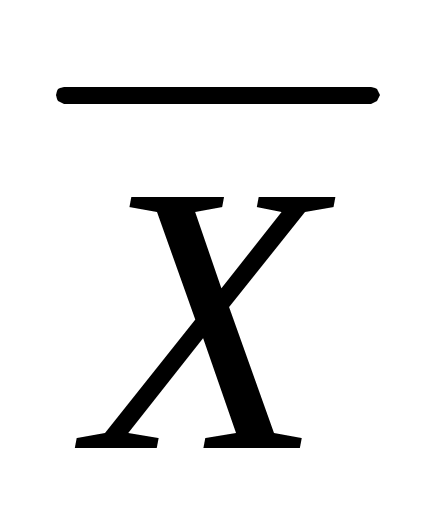 для гипотетического бесконечного количества выборок имеет распределение N ( х, для гипотетического бесконечного количества выборок имеет распределение N ( х, 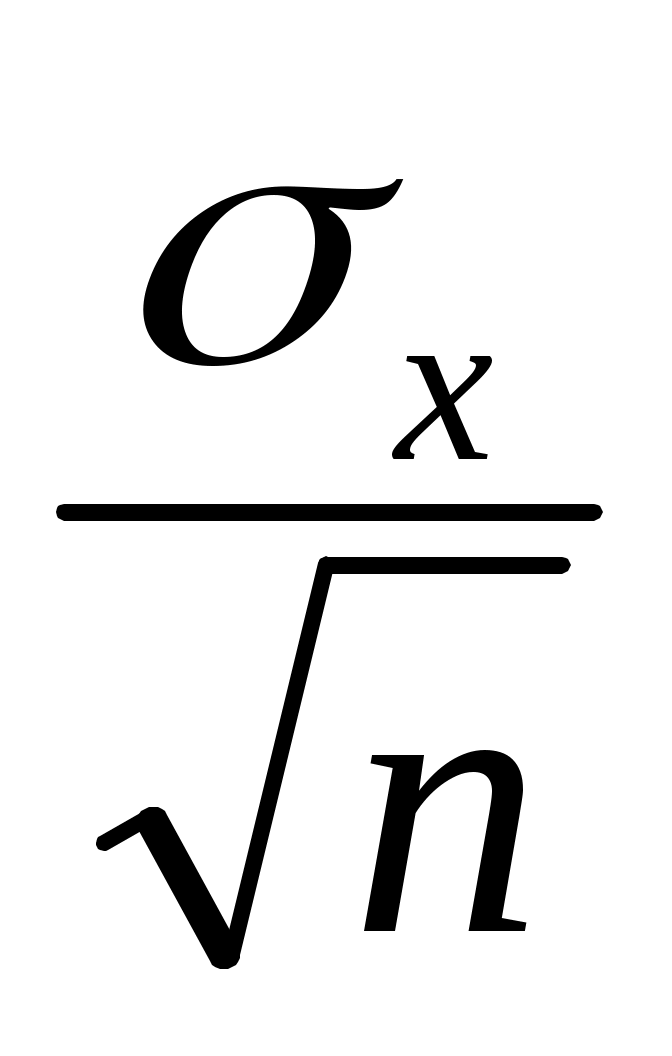 ). ).
Вспомним теперь, что такое стандартизованное нормальное распределение, и попытаемся понять, как оно связано с нестандартизованным распределением случайной величины 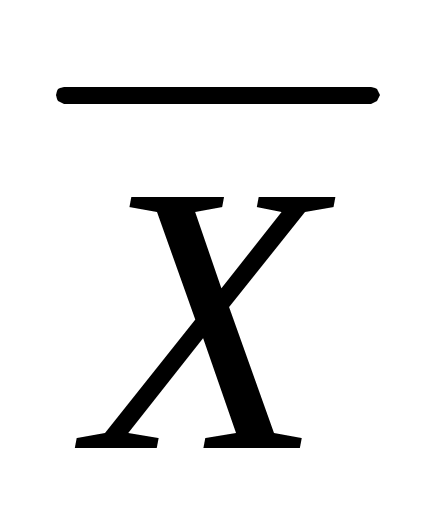 (напомним, что значений средних мы рассматриваем как реализации некоторой случайной величины). (напомним, что значений средних мы рассматриваем как реализации некоторой случайной величины).
Нетрудно видеть , что величина
Z = 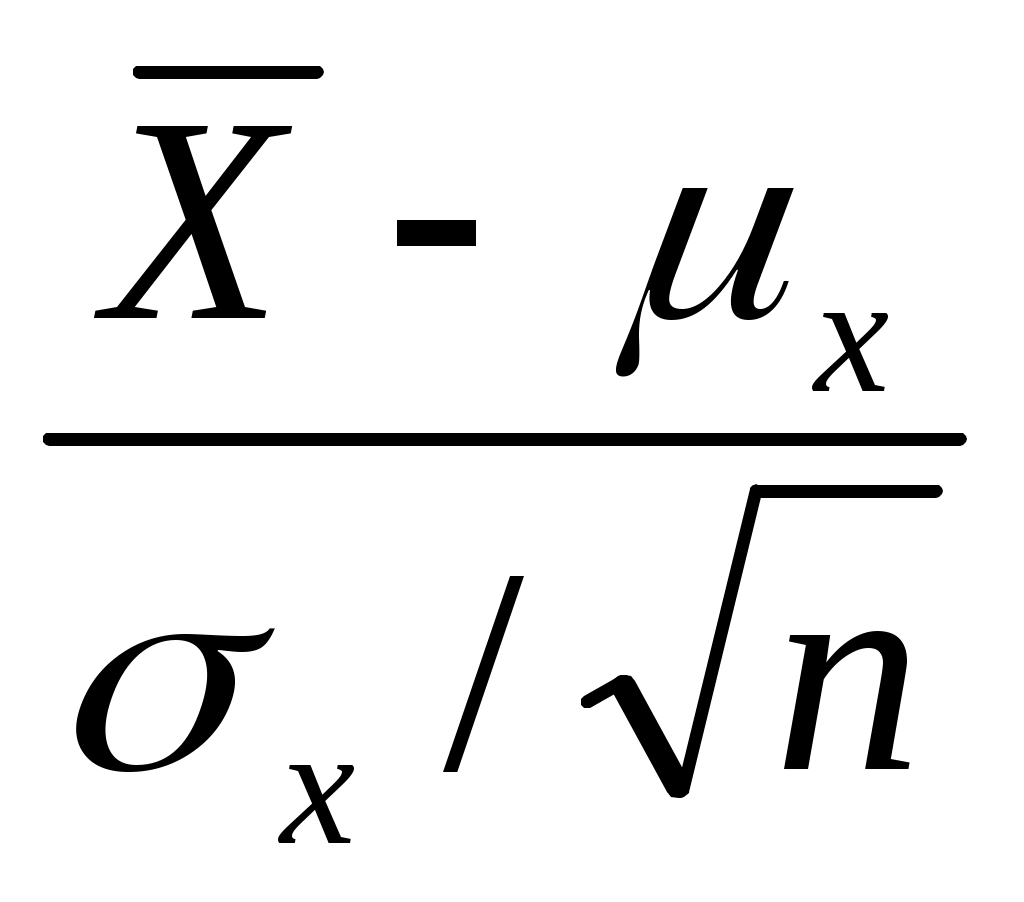 (6.2) (6.2)
имеет стандартизованное нормальное распределение.
Если мы зададимся целью найти тот интервал, в который попадает, скажем, 95% значений стандартизированной нормально распределенной величины, то, пользуясь известной таблицей, быстро установим, что этот интервал имеет вид
( -1,96; +1,96).
Использовав это обстоятельство применительно к величине (2), получим, что 95% значений этой величины удовлетворяет соотношению:
- 1,96 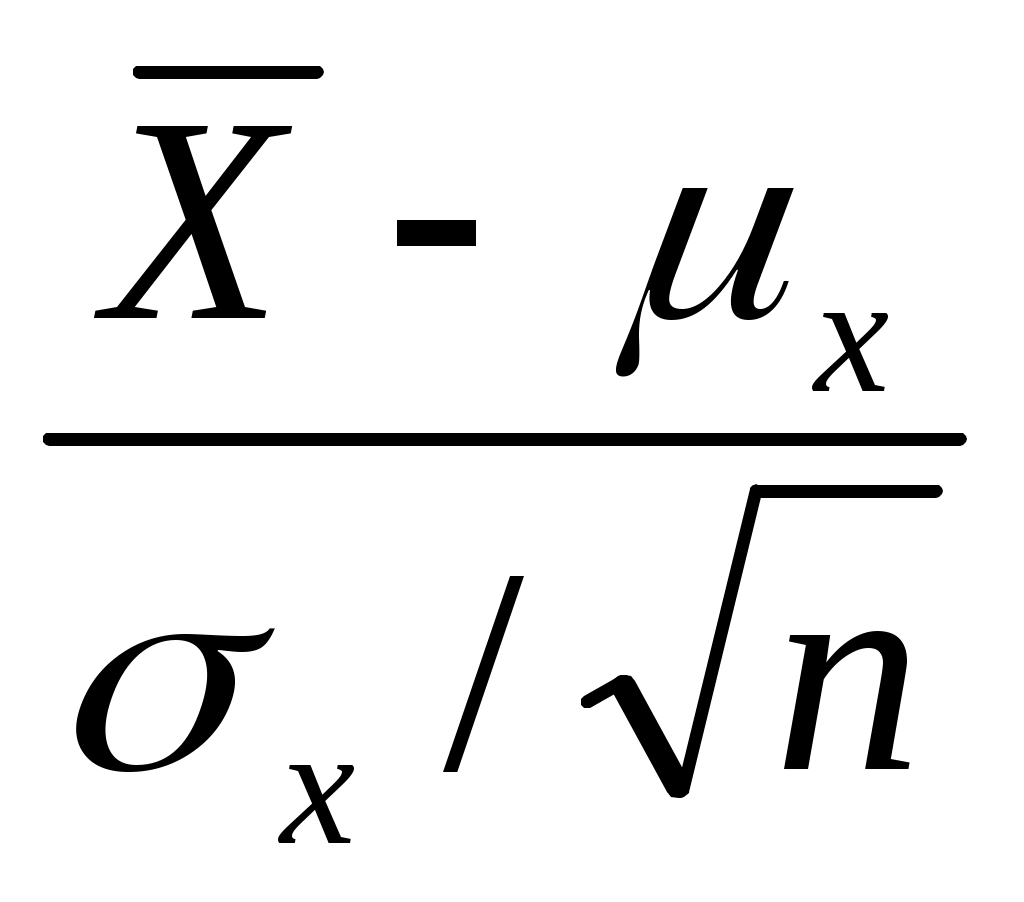 1,96 1,96
Значит, 95% значений случайной величины Х удовлетворяет условию
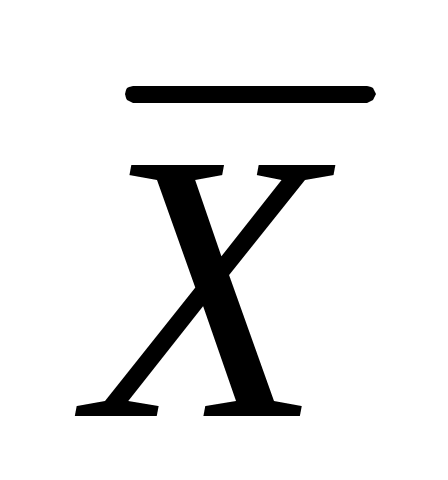 – 1,96 – 1,96 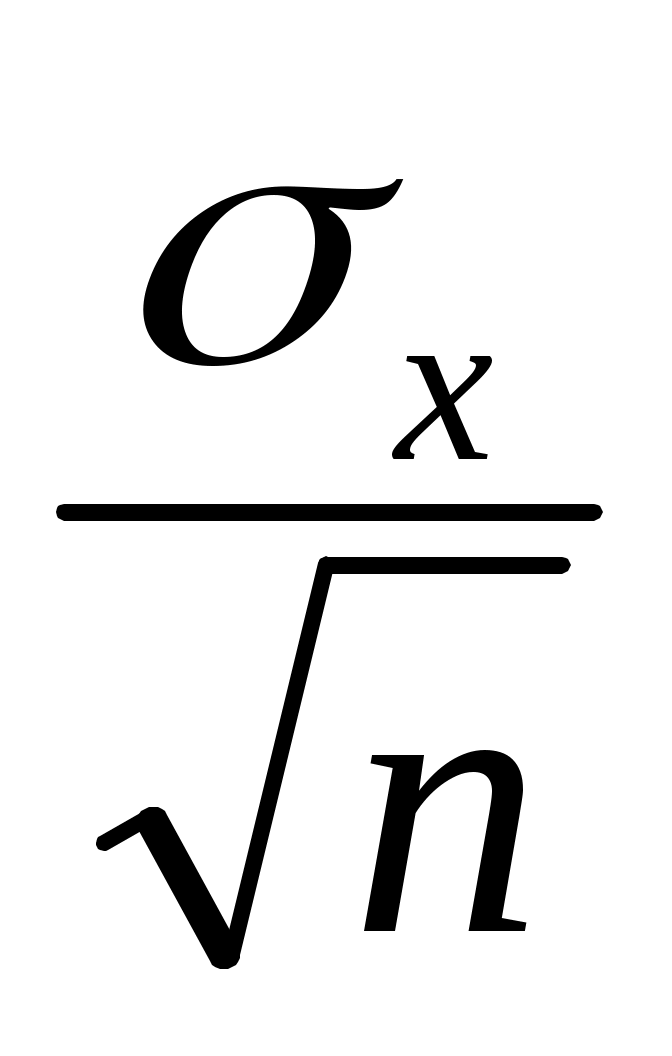 х х 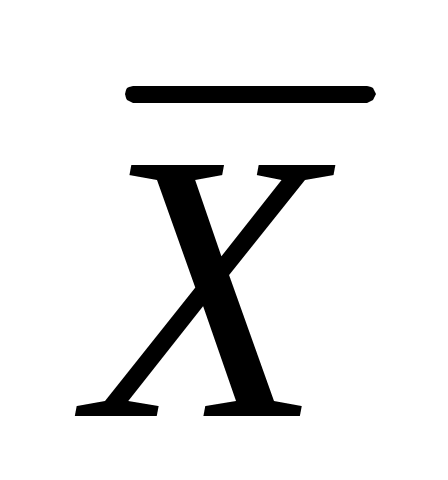 + 1,96 + 1,96 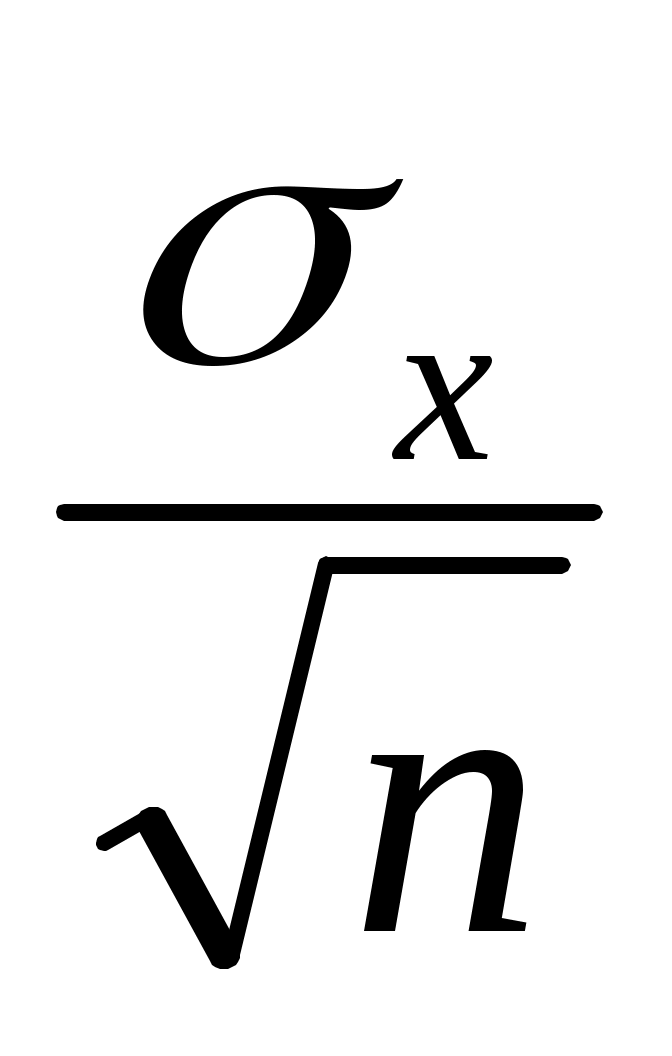 (6.3) (6.3)
или, что то же самое,
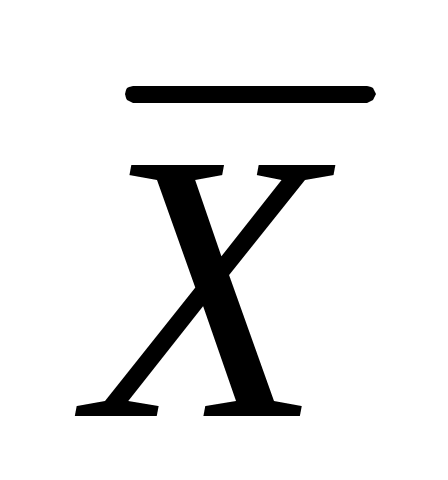 – 1,96 – 1,96 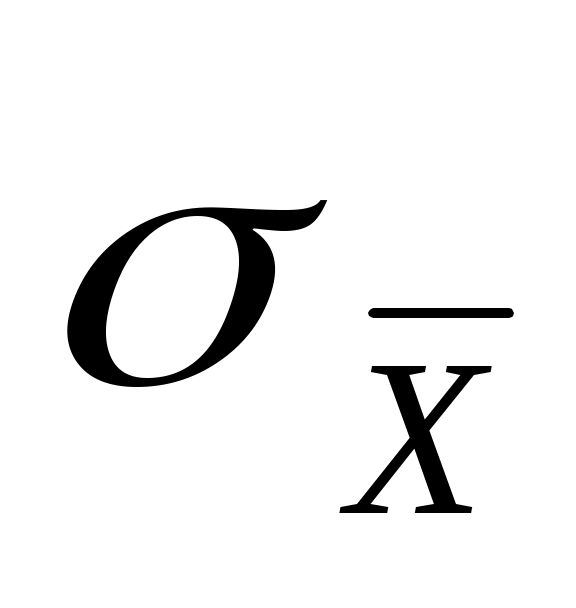 х х 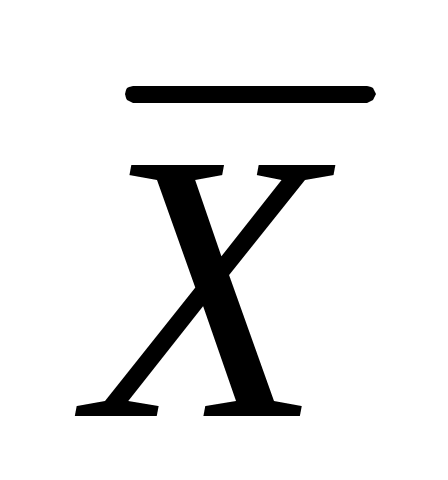 + 1,96 + 1,96 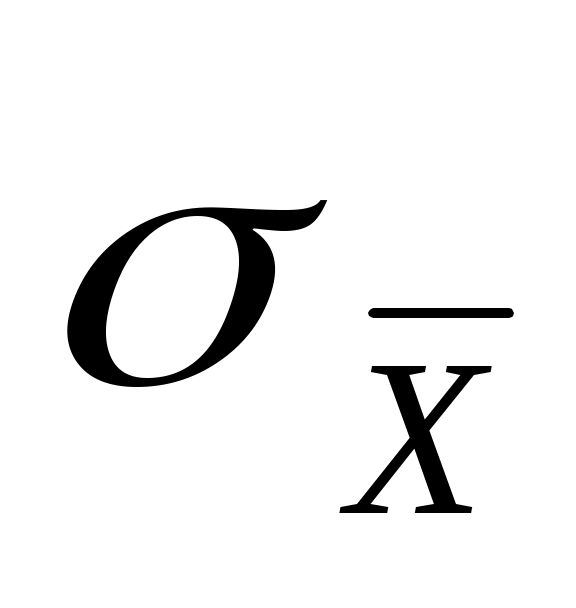
Опр. Интервал (6.3) называется 95-%м доверительным интервалом для математического ожидания.
Если мы захотим, чтобы аналогичному условию удовлетворяло 90% выборочных значений среднего арифметического, то должны число 1,96 заменить на 1,64; для 99% должны использовать множитель 2,57 и т.д.
К соотношению типа (6.3) можно придти и по-другому.
Рассмотрим рис. 1. Теоретически мы знаем, что Р % (выше – 95%) средних арифметических, рассчитанных для разных выборок, лежит вокруг х в интервале, обозначенном овалом.
  

 х - zx х х - zx х 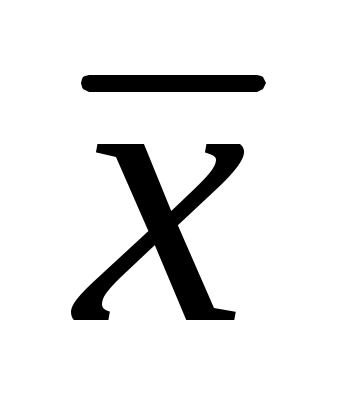 выб х + zx выб х + zx

Рис.6.1. Ситуация, когда доверительный интервал (обозначен прямоугольником) «накрывает» математическое ожидание. Овал отвечает тому интервалу , в который попадают Р % выборочных средних арифметических
Теперь представим себе реальную ситуацию. У нас имеется единственная выборка и единственное значение среднего арифметического, вычисленное для нее. Обозначим его 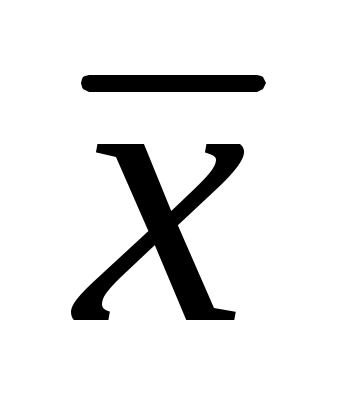 выб. Нам надо выяснить,где находится х. На помощь приходит соображение о том, что выб. Нам надо выяснить,где находится х. На помощь приходит соображение о том, что 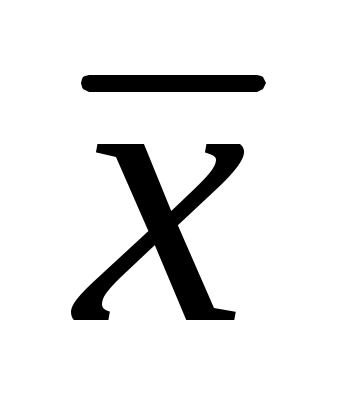 выб., очевидно, с вероятностью Р% попадает в «овальный» интервал. Поэтому, вероятно, логично было бы предположить, что х с такой же вероятностью попадет в интервал такого же размера, но с центром не в х, а в выб., очевидно, с вероятностью Р% попадает в «овальный» интервал. Поэтому, вероятно, логично было бы предположить, что х с такой же вероятностью попадет в интервал такого же размера, но с центром не в х, а в 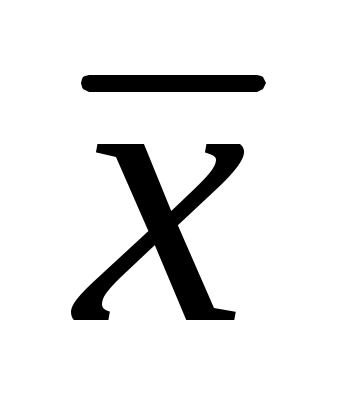 выб. Этот интервал обозначен на рисунке прямоугольником. С помощью этого интервала мы можем с вероятностью Р% «поймать» математическое ожидание. Ясно, что это – интервал типа (3) (для последнего Р = 95%). выб. Этот интервал обозначен на рисунке прямоугольником. С помощью этого интервала мы можем с вероятностью Р% «поймать» математическое ожидание. Ясно, что это – интервал типа (3) (для последнего Р = 95%).
Конечно, не исключено, что 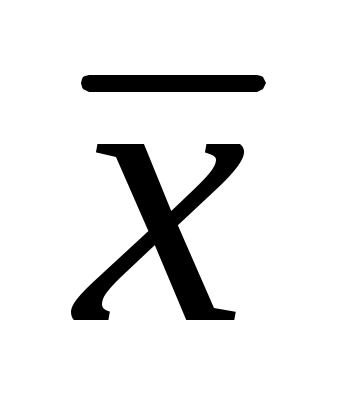 выб не попадет в «овальный» интервал. Тогда мы мы будем иметь ситуацию, отраженную на рис.2. Ясно, что в таком случае реальное математическое ожидание не попадет в построенный для него интервал, не будем нами «поймано». выб не попадет в «овальный» интервал. Тогда мы мы будем иметь ситуацию, отраженную на рис.2. Ясно, что в таком случае реальное математическое ожидание не попадет в построенный для него интервал, не будем нами «поймано».

  
 х - zx х х + zx х - zx х х + zx 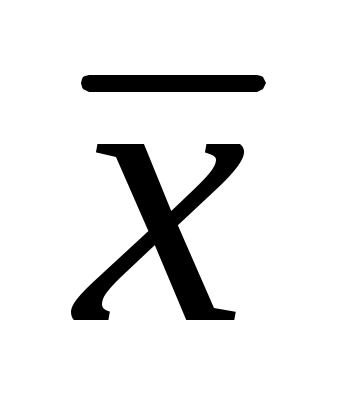 выб выб

Рис. 6.2. Ситуация, когда математическое ожидание лежит вне доверительного интервала (последний обозначен прямоугольником. Овал отвечает тому интервалу , в который попадают Р % выборочных средних арифметических СДЕЛАТЬ «ЗАРУБКИ» НА ОСИ
Изобразим то же по-другому, прибегнув к изображению функции плотности распределения средних арифметических для выборок объема n, из генеральной совокупности с математическим ожиданием . Случаи, когда построенный по некоторому выборочному значению 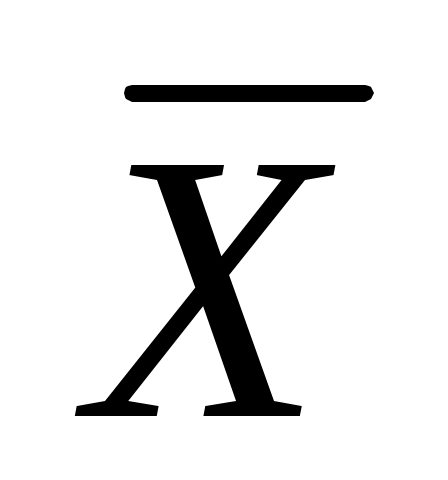 доверительный интервал содержит , либо не содержит генеральное математическое ожидание, отражены, соответственно, на рисунка 6.3 и 6.4. доверительный интервал содержит , либо не содержит генеральное математическое ожидание, отражены, соответственно, на рисунка 6.3 и 6.4.
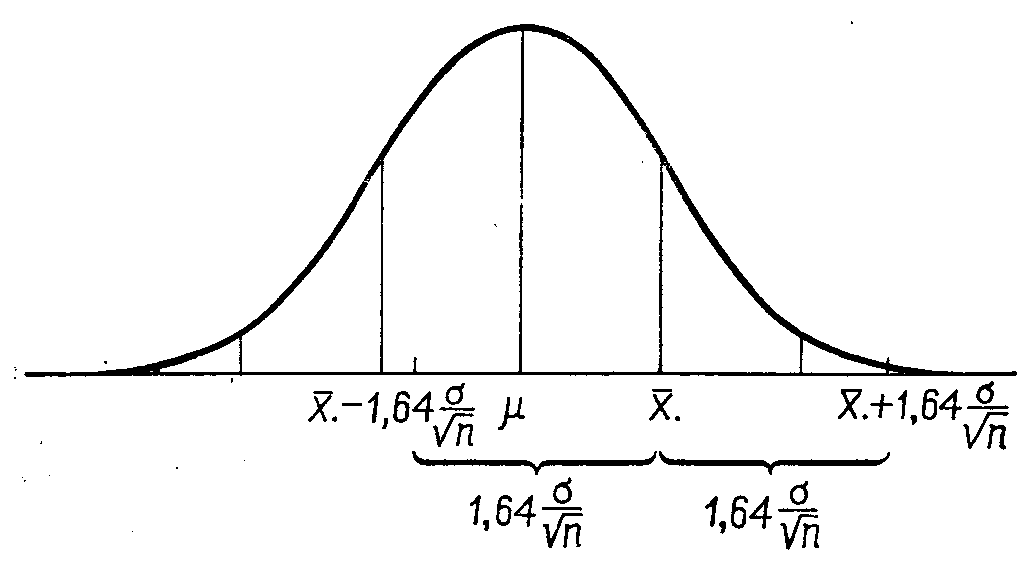
Рис. 6.3. Иллюстрация случая, когда интервал, установленный относительно 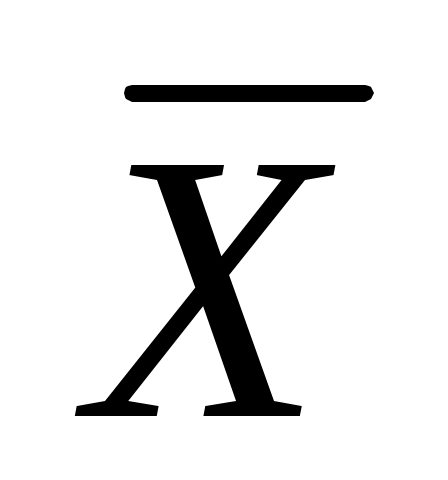 , содержит в своих границах.48 НА РИСУНКЕ УБРАТЬ ТОЧКУ ПРИ Х с чертой. !!!!!!!!!!!!!!!!!!! , содержит в своих границах.48 НА РИСУНКЕ УБРАТЬ ТОЧКУ ПРИ Х с чертой. !!!!!!!!!!!!!!!!!!!
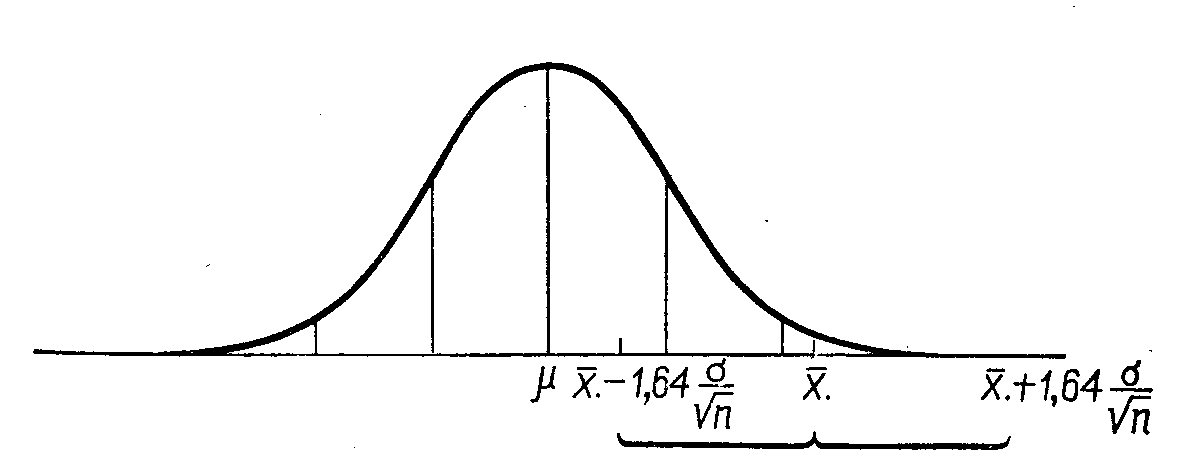
Рис. 6.4. Иллюстрация случая, когда интервал, установленный относительно 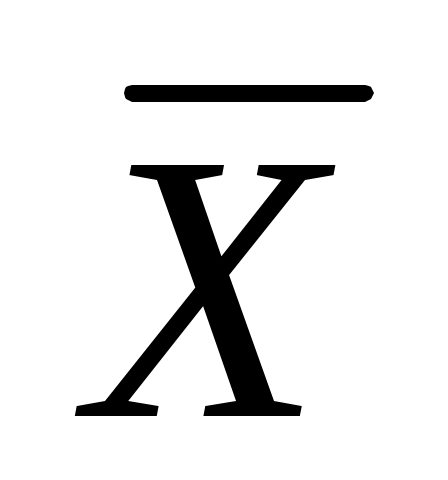 , не содержит в своих границах.49 НА РИСУНКЕ УБРАТЬ ТОЧКУ ПРИ Х с чертой. !!!!!!!!!!!!!!!!!!! , не содержит в своих границах.49 НА РИСУНКЕ УБРАТЬ ТОЧКУ ПРИ Х с чертой. !!!!!!!!!!!!!!!!!!!
Возвращаясь к соотношению (6.1) и сравнивая его с (6.3), можно сказать, что для математического ожидания имеет место соотношение:
= z 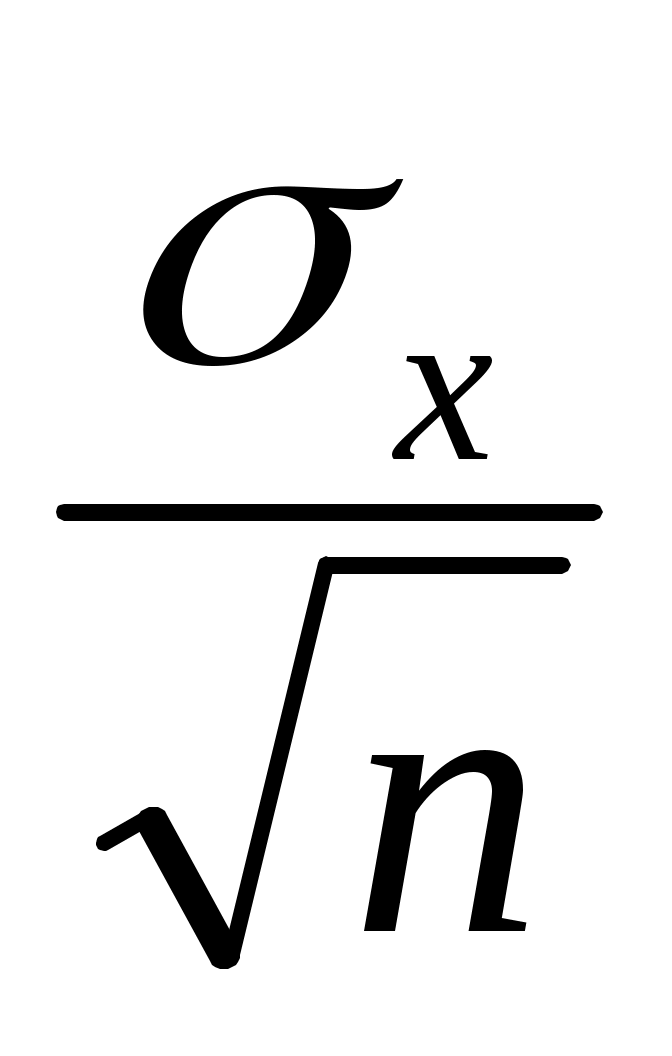 (6.4) (6.4)
Другими словами, соотношение (6.1) превращается в
Р (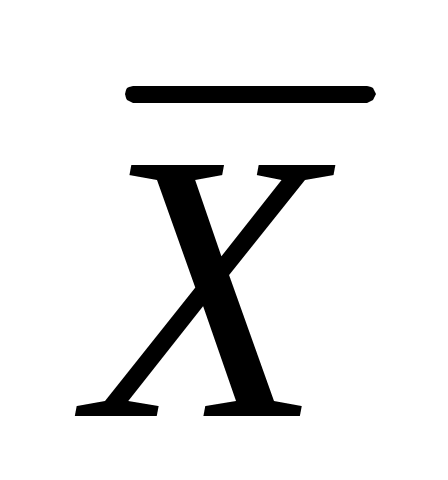 - z - z 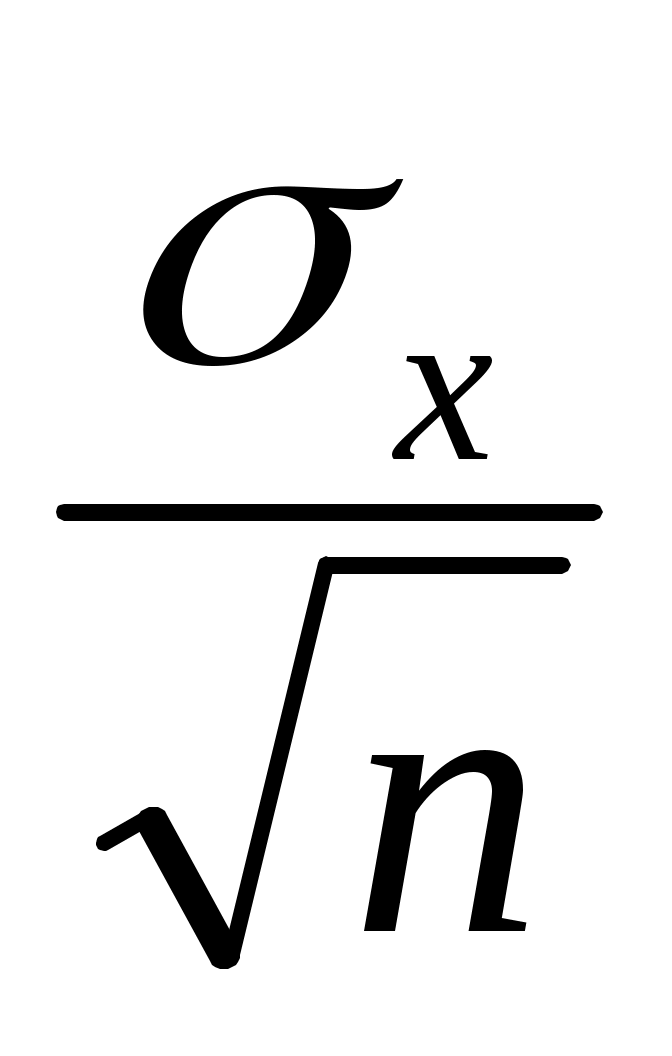 х х 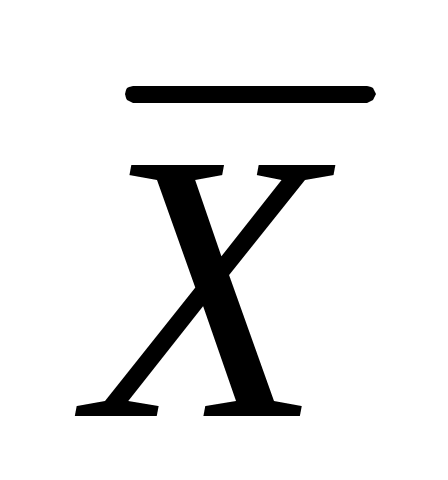 + z + z 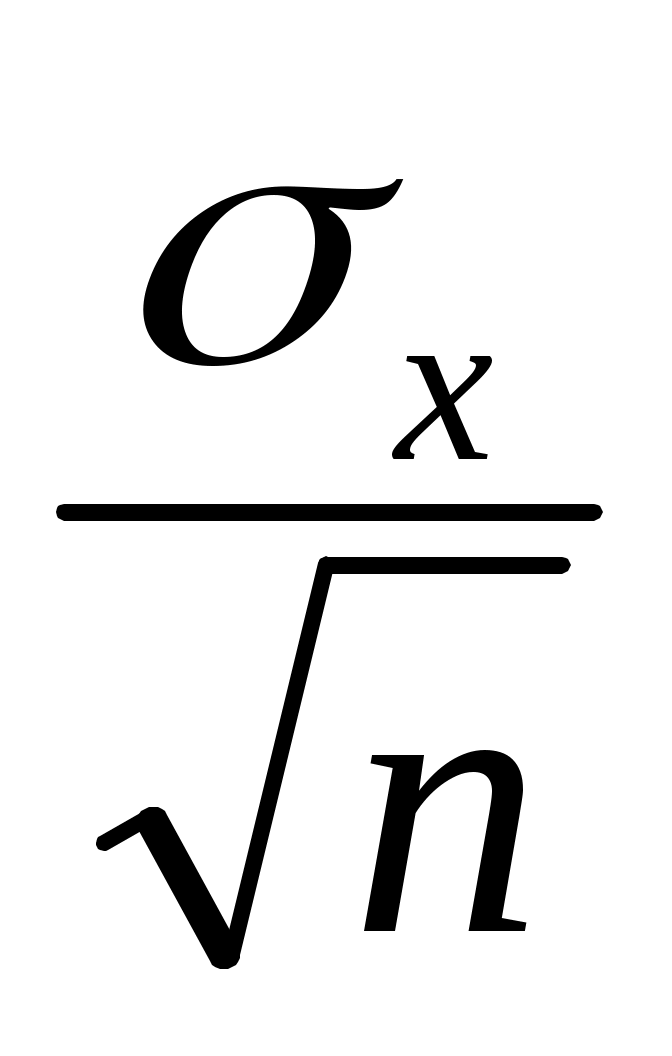 ) = 1 - , (6.5) ) = 1 - , (6.5)
где z определяется по таблице, исходя из выбранного .
Опр. Интервал (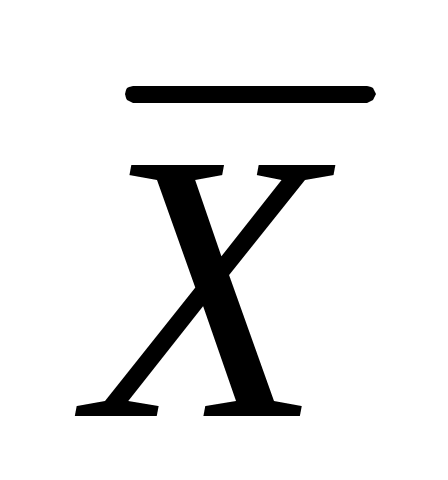 - , - , 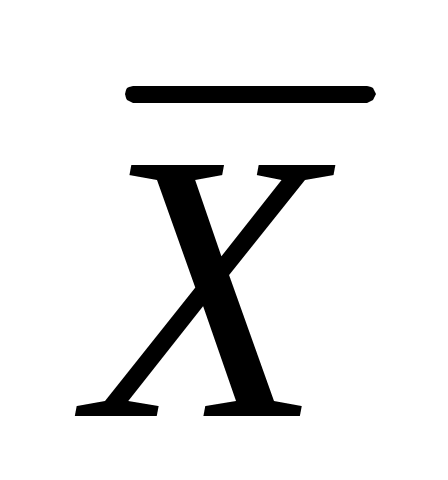 + ), или, что то же самое, интервал + ), или, что то же самое, интервал
(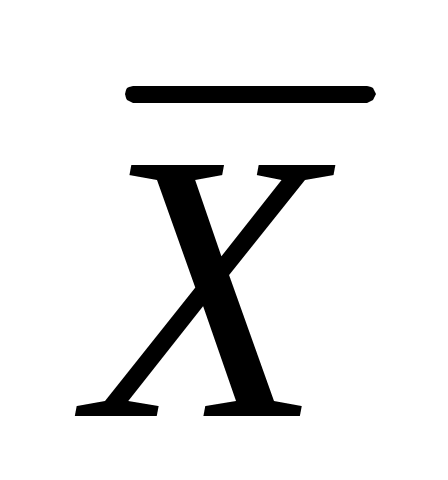 - z - z 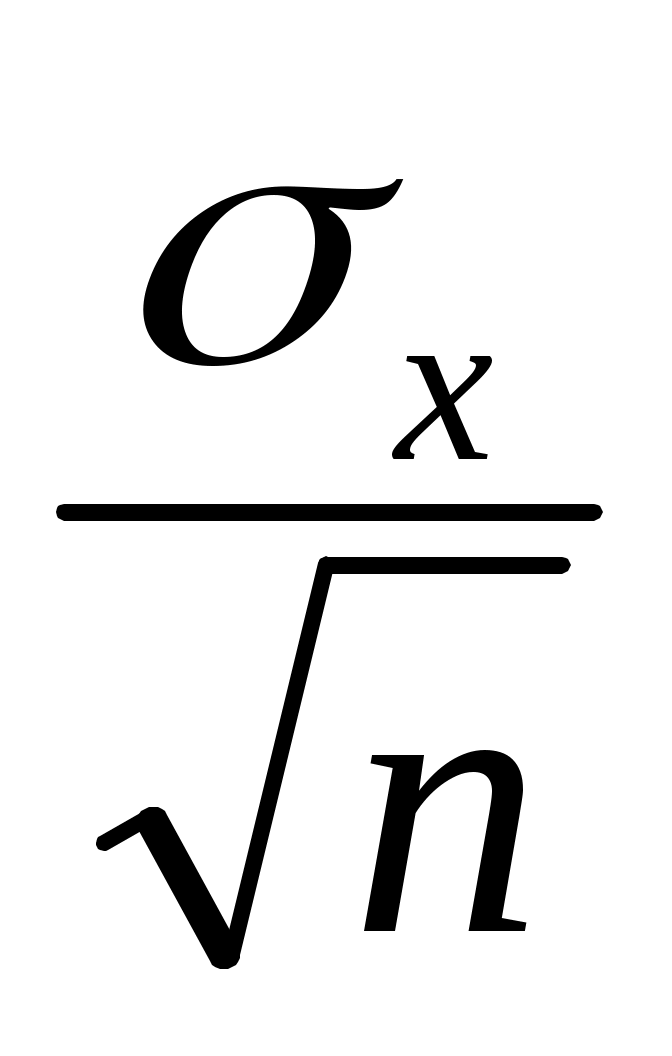 , , 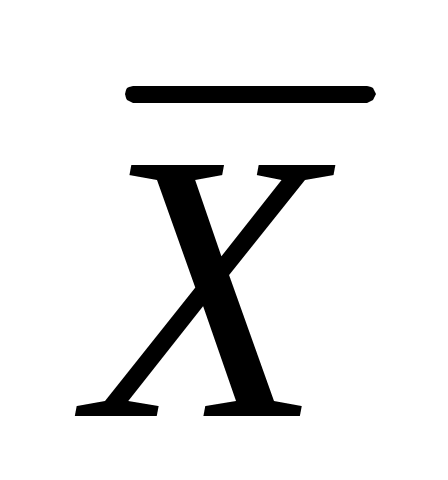 + z + z 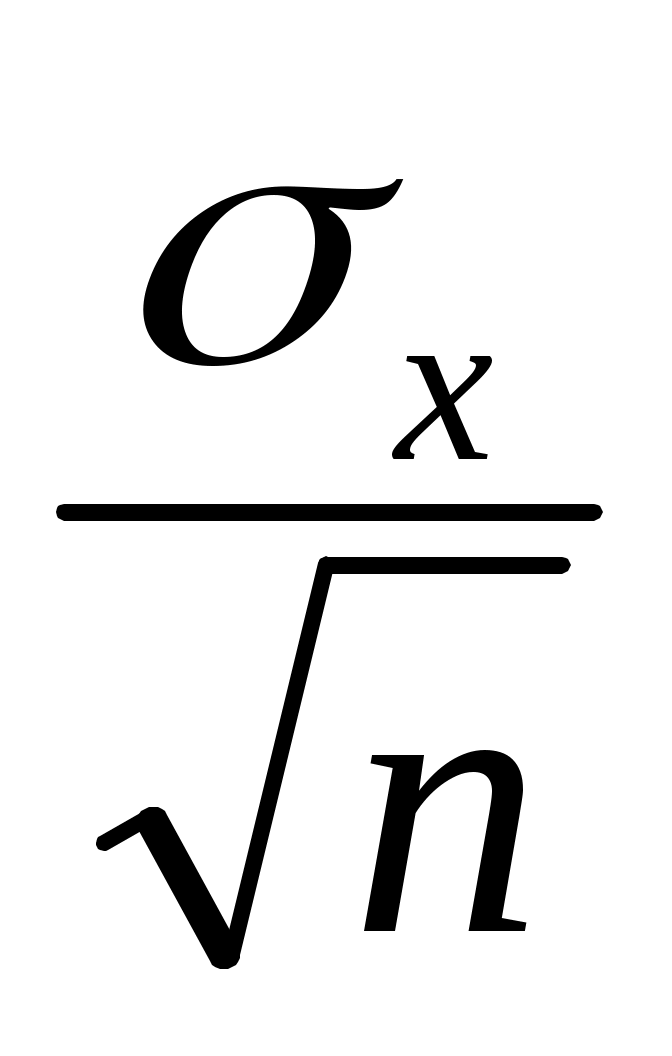 ) )
называется доверительным интервалом для х .
Построение такого интервала - это и есть результат переноса сведений о выборочном среднем (коим является значение х) на генеральную совокупность.
Опр. называется уровнем значимости доверительного интервала.
Как уже было сказано, он задается исследователем. Его выбор обуславливается содержательными соображениями. Чаще всего полагают, что = 0,05. Такой выбор означает, что 95-процентной уверенности в том, что генеральное ожидание принадлежит заданному интервалу, нам достаточно для того, чтобы считать это утверждение практически всегда верным. Другими словами, уровень значимости – это такая вероятность относительно которой мы предполагаем, что события, имеющие такую (или меньшую) вероятность, практически не происходят. Подчеркнем, что с оценкой подобной вероятности человек часто сталкивается в обыденной жизни. Именно на базе подобных оценок мы очень часто принимаем те или иные решения. К примеру, предположим, что по дороге на работу мы должны пройти мимо строящегося дома. Мы можем не давать себе в этом отчета, но где-то в подсознании у нас всегда будет происходить оценка вероятности того, что нам на голову свалится кирпич. Если нам случалось много раз проходить мимо этого дома без всяких неприятных последствий и мы никогда не слышали о том, что на кого-то что-то здесь свалилось, мы будем считать, что вероятность неприятности слишком мала для того, чтобы ее следовало принимать во внимание при принятии решения о нашем маршруте, и мы смело идем мимо стройки, не переходя на другую сторону улицы. В математической статистике обычно считается, что «слишком мала» означает «не более 5%». Напротив, если мы вчера прочитали в газете, что позавчера именно на этой стройке кирпич-таки свалился кому-то на голову50, то мы, наверное, решим, что вероятность неприятности достаточно велика для того, чтобы ее надо было учитывать в своем поведении, и мы делаем крюк, чтобы обойти стройку, даже если опаздываем на работу. Опыт применения математической статистики говорит о том, что «достаточно велика» означает «превышает 5%».
Ясно, что, если суть задачи требует более надежной информации, то мы должны понизить уровень значимости, скажем, полагать, что он равен 0,01. Если, напротив, нас вполне устраивает меньшая уверенность, скажем, в 90%, то будем полагать, что = 0,1.
Мы вернемся к обсуждению смысла уровня значимости ниже, при рассмотрении способов проверки статистических гипотез (см. п. 7.2).
Значение z находится из таблицы нормального распределения. Величины z и (а, стало быть, z и Р) полностью определяют друг друга. Определение по таблице значения z для произвольного уровня доверительности интервала (величину разности (100 – уровень доверительности) надо поделить на 2, чтобы искать ).
Ясно, что исследователю всегда хочется, чтобы были поменьше и уровень значимости (а Р – побольше), и длина доверительного интервала (и, значит, z). Однако, к сожалению, законы природы так устроены, что уменьшение уровня значимости влечет за собой увеличение доверительного интервала. Поясним сказанное с помощью следующего рассуждения. Нетрудно понять, что, если Х, к примеру, – возраст, выборочное среднее арифметическое значение которого оказалось равным 40 годам, то с вероятностью, практически равной 100% (т.е. 0, математическое ожидание будет находиться в интервале (40 лет —100 лет, 40 лет + 100 лет). Однако от этой информации вряд ли может быть какая-либо практическая польза. Напротив, вероятность того, что генеральное математическое ожидание в той же ситуации в точности равно 40 годам (т.е. равен нулю доверительный интервал), практически нулевая (выборка всегда хотя бы в какой-то мере отличается от генеральной совокупности, и поэтому выборочная статистика, как правило, будет отличаться от значения соответствующего генерального параметра).51
Отметим, что x2 социологу, как правило, неизвестно (хотя бывают ситуации, когда генеральную дисперсию признака удается хотя бы как-то оценить по каким-либо косвенным данным – скажем, воспользоваться результатами переписи, данными какого-то исследования, проведенного другим социологом и т.д.). Поэтому его вынуждены заменять выборочной дисперсией sx2 . Тогда, казалось бы, должно иметь место соотношение 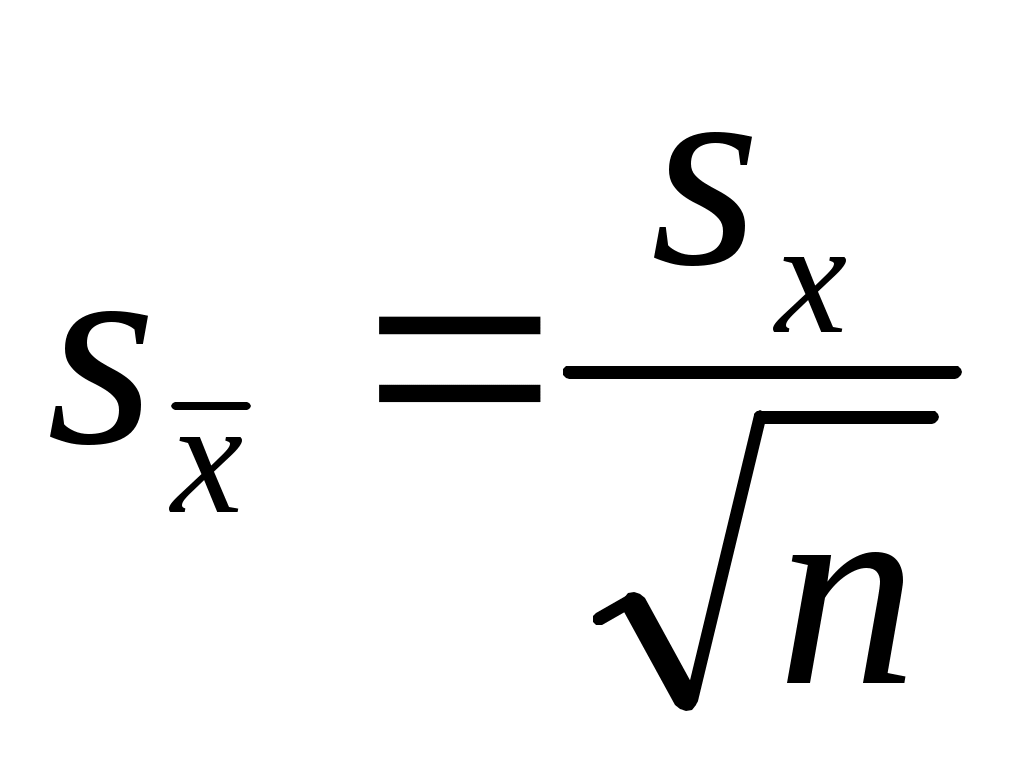 и, следовательно, равенство (6.4) заменяется на равенство = z и, следовательно, равенство (6.4) заменяется на равенство = z 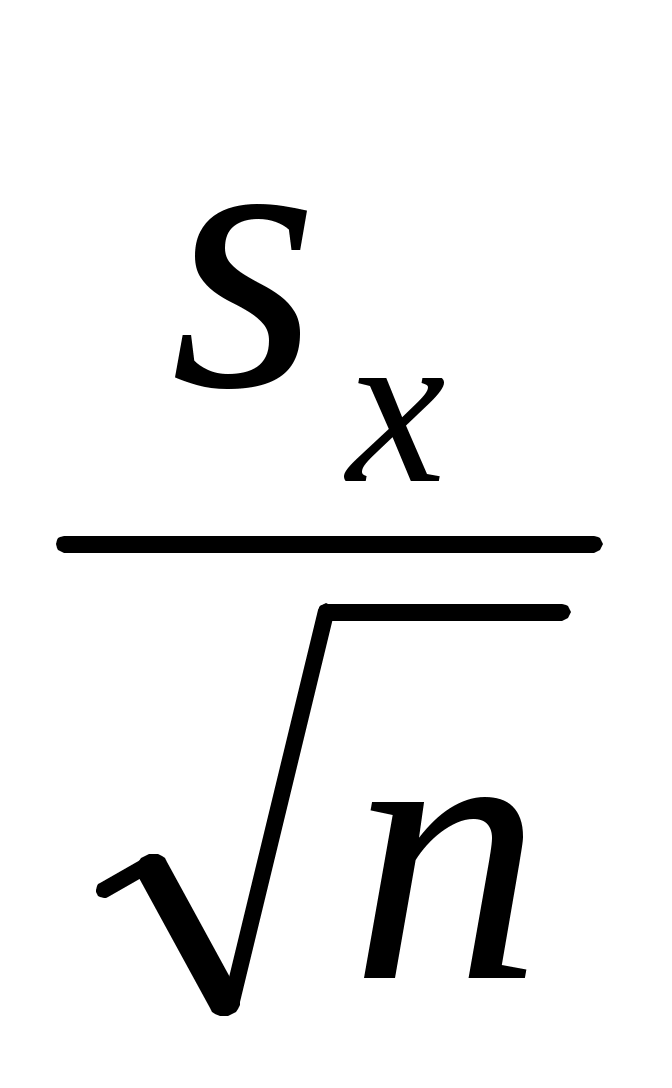 . Однако это не так. Дело в том, что нормальное распределение при построении доверительного интервала для математического ожидания, вообще говоря, используется только при заданной генеральной дисперсии. В тех случаях, когда происходит замена x2 на sx2 нормальное распределение «превращается» в распределение Стьюдента. Коротко опишем, как в таких случаях надо действовать, не приводя строгих рассуждений, объясняющих описываемый алгоритм. . Однако это не так. Дело в том, что нормальное распределение при построении доверительного интервала для математического ожидания, вообще говоря, используется только при заданной генеральной дисперсии. В тех случаях, когда происходит замена x2 на sx2 нормальное распределение «превращается» в распределение Стьюдента. Коротко опишем, как в таких случаях надо действовать, не приводя строгих рассуждений, объясняющих описываемый алгоритм.
Если мы пользуемся выборочной оценкой sх дисперсии признака , то доверительный интервал для х приобретает вид:
(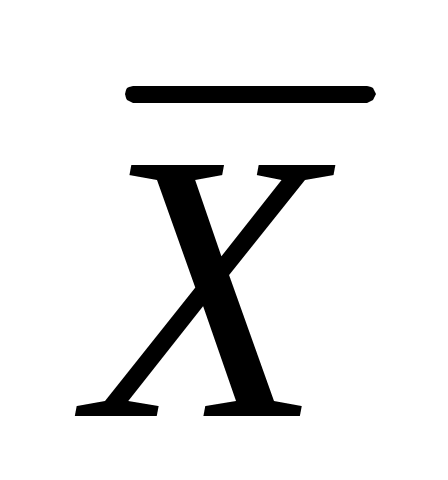 - tn-1 - tn-1 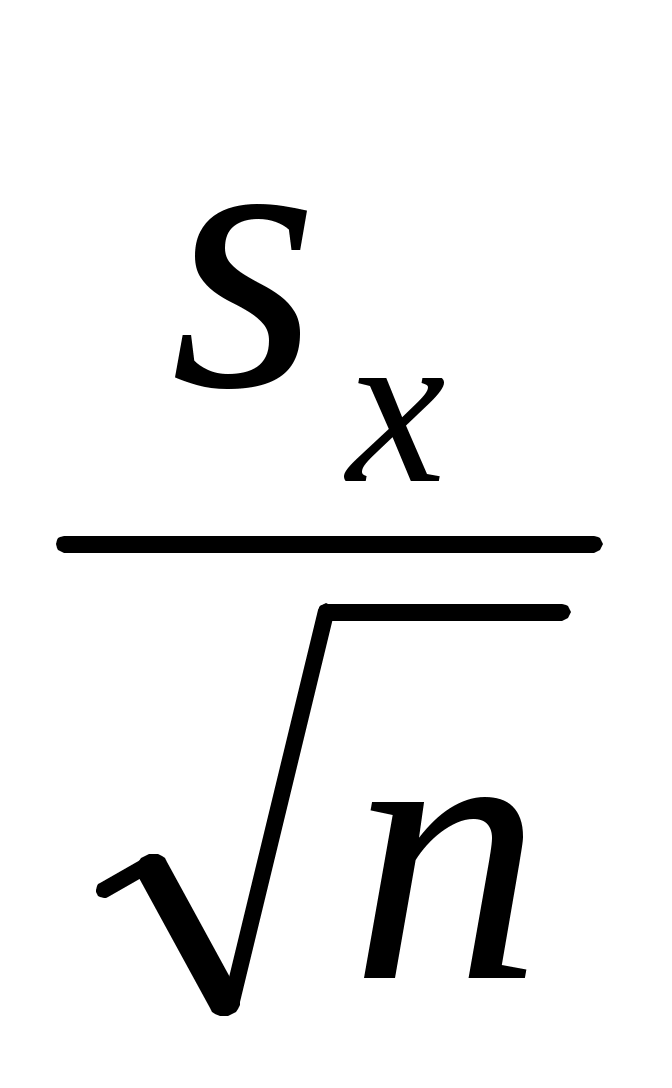 , , 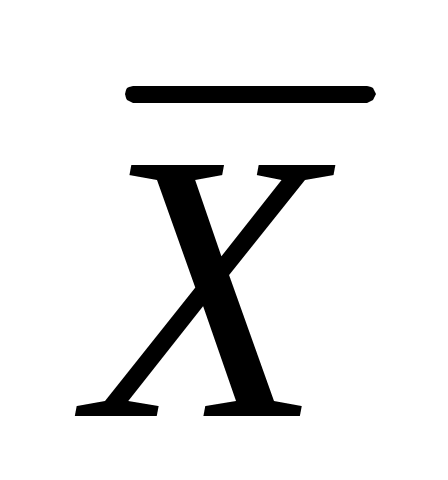 + tn-1 + tn-1 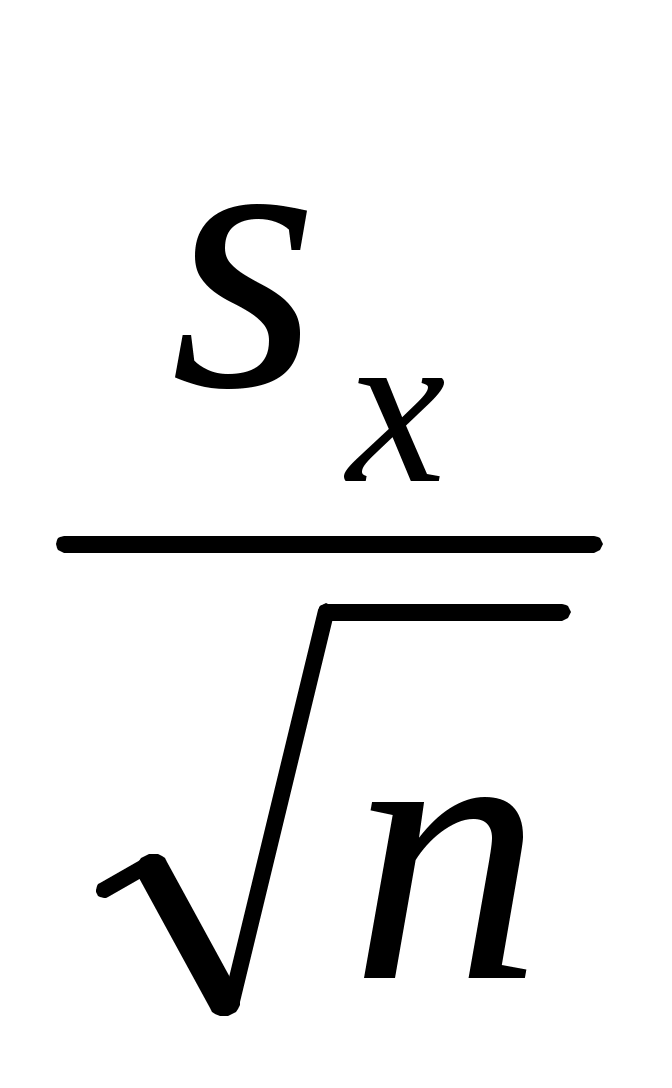 ), ),
где t – величина, найденная способом, аналогичным тому, с помощью которого мы искали z, но с использованием таблицы для распределения Стьюдента с числом степеней свободы, равным (n – 1). Другими словами, величина, полученная из (2) заменой x на sх, будет иметь не нормальное распределение, а распределение Стьюдента:
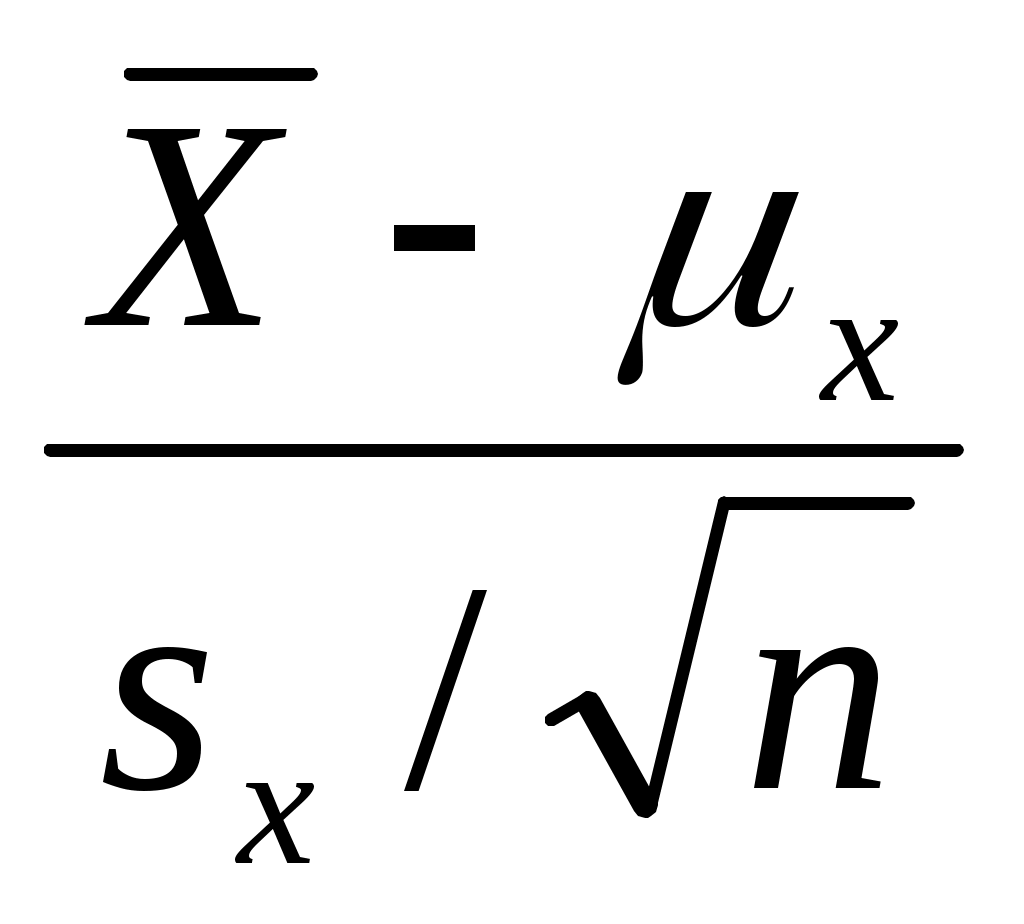 tn-1
(Заметим, что нельзя пользоваться нормальным распределением и при малых объемах выборки, даже если х известна; однако некоторая корректировка величины (2) все же приводит ее распределение к нормальному. А именно, нормально распределенной будет величина:
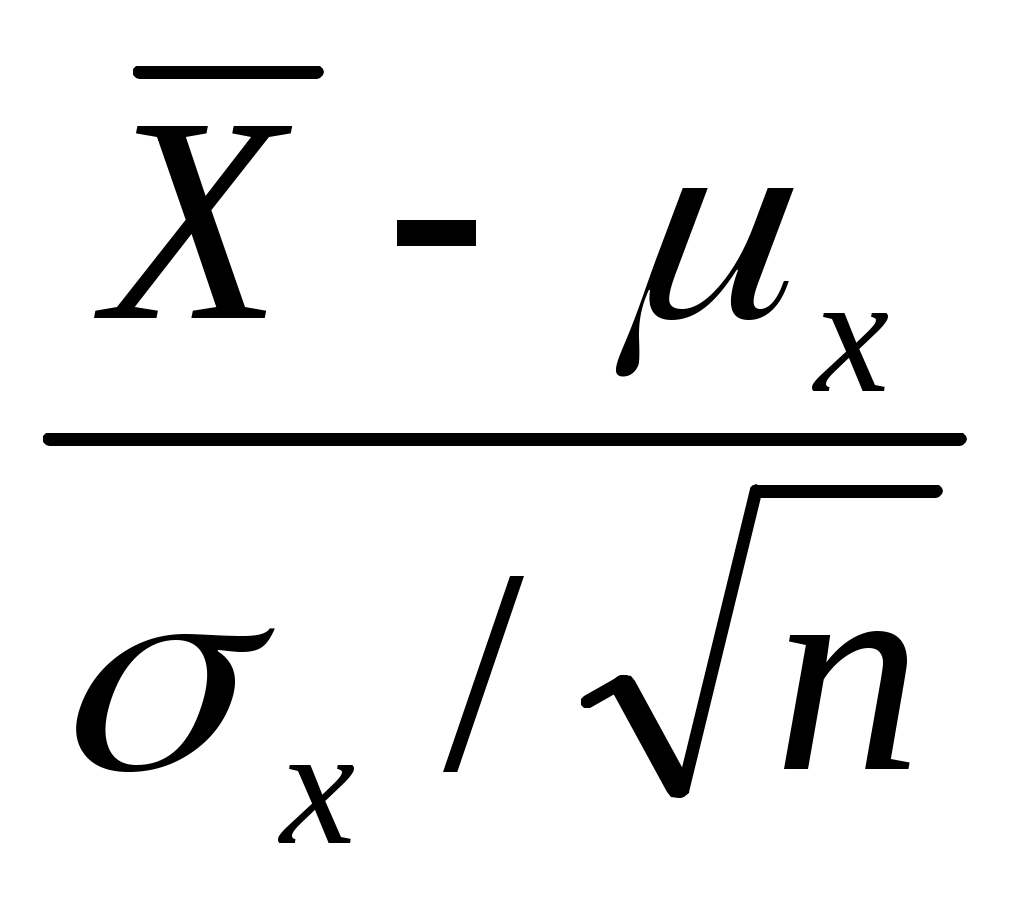 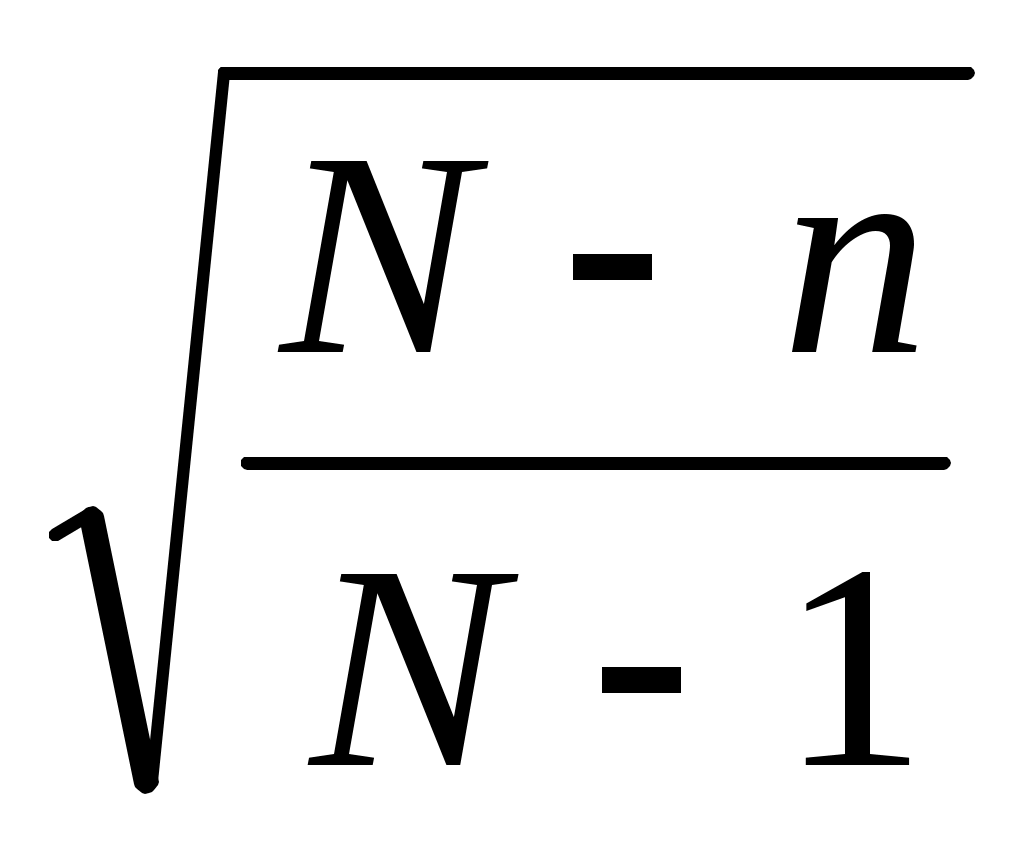 . .
При бесконечной генеральной совокупности эта поправка не имеет смысла.)
Но, как мы отмечали при обсуждении темы 3 (п.3.4), при достаточно большом объеме выборки распределение Стьюдента можно считать приблизительно совпадающим с нормальным, поэтому при большой выборке можно пользоваться нормальным распределением (т.е. вместо t находить z ) даже в том случае, когда генеральное значение х мы вынуждены заменить на выборочную его оценку sх.
Обычно применяют следующее правило52.
Да
  известна используем z известна используем z
нет
да
В ыборка используем z; заменяем на s ыборка используем z; заменяем на s
30
нет
используем t
заменяем на s
Лишний раз повторим сказанное: относительно доверительного интервала для математического ожидания необходимо учитывать, что вид этого интервала зависит от того,
- известно ли ;
- если неизвестно, то вместо него выступает s (которое рассчитывается либо по заданному набору значений признака, либо по частотной таблице), а величина z заменяется на tn-1;
- указанная в предыдущем пункте замена может не осуществляться, если объем выборки >30.
6.2. Определение объема выборки
Иногда ситуация складывается так, что мы из каких-либо содержательных (внешних по отношению к задаче построения доверительного интервала) соображений можем задать максимально возможное значение величины , фигурирующую в определении доверительного интервала. В таком случае имеет смысл следующее определение.
Опр. Максимально возможное значение называется предельной ошибкой выборки для признака x.
Нетрудно видеть, что предельная ошибка выборки - это та ошибка, которую мы допускаем, желая, чтобы генеральный показатель с заданным уровнем значимости находился в некотором заданном интервале.
Если и предельная ошибка выборки , и уровень значимости будут заданы (а уровень значимости, как известно, определяет величину z), то приведенные выше соотношения позволят найти нижнюю границу объема выборки. Это следует из того, что о имеет место соотношение:
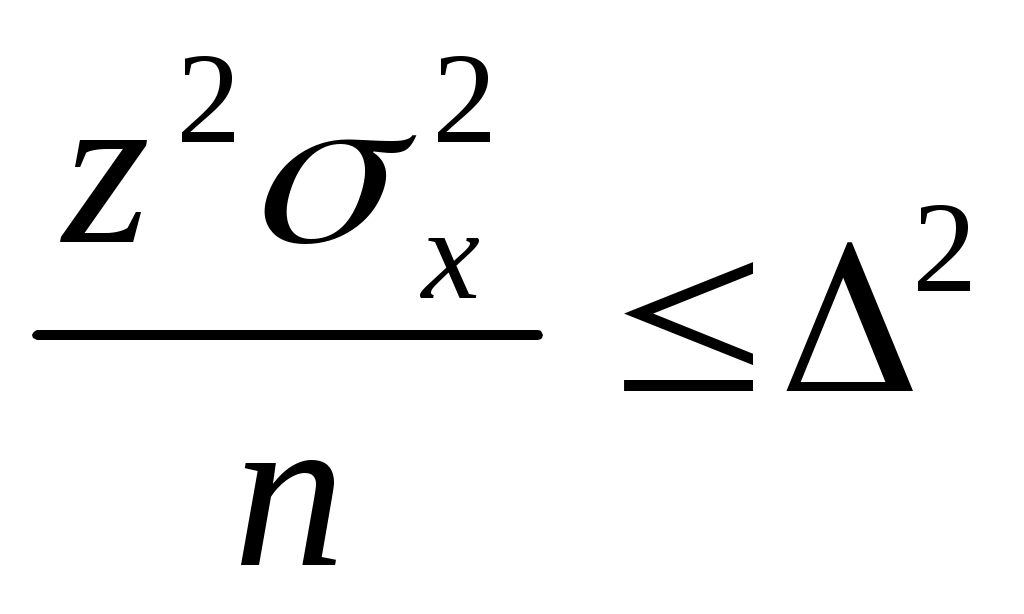 , ,
и, следовательно, верно неравенство
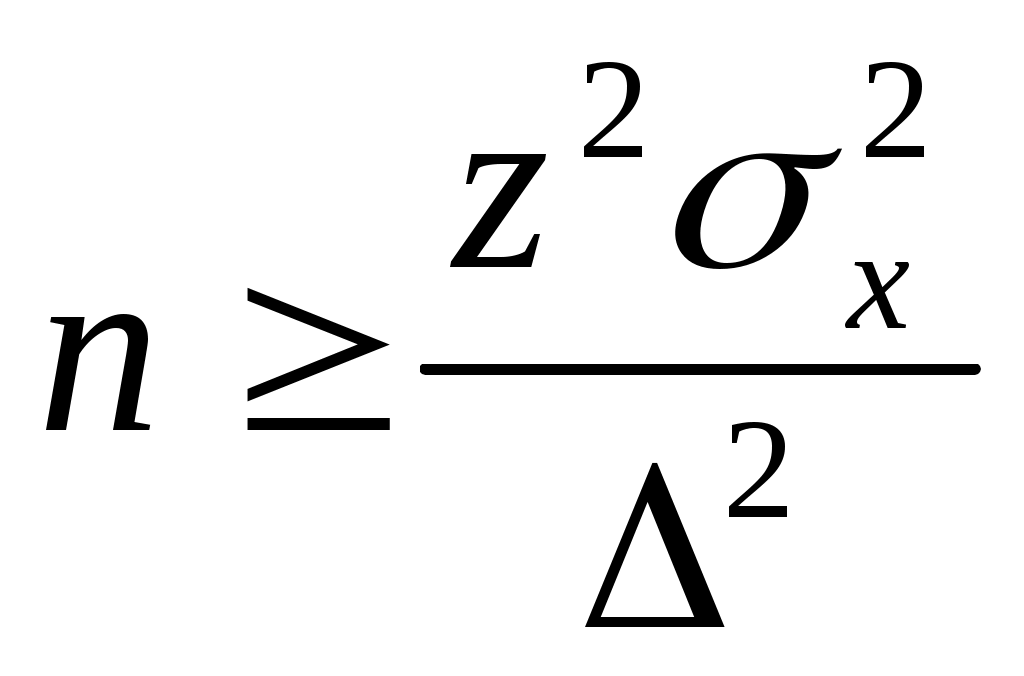 . .
(Отметим, что приведенные формулы лишь приблизительны. Ими можно пользоваться, если доля выборки в генеральной совокупности достаточно мала. Обычно считают, что должно выполняться соотношение
f = 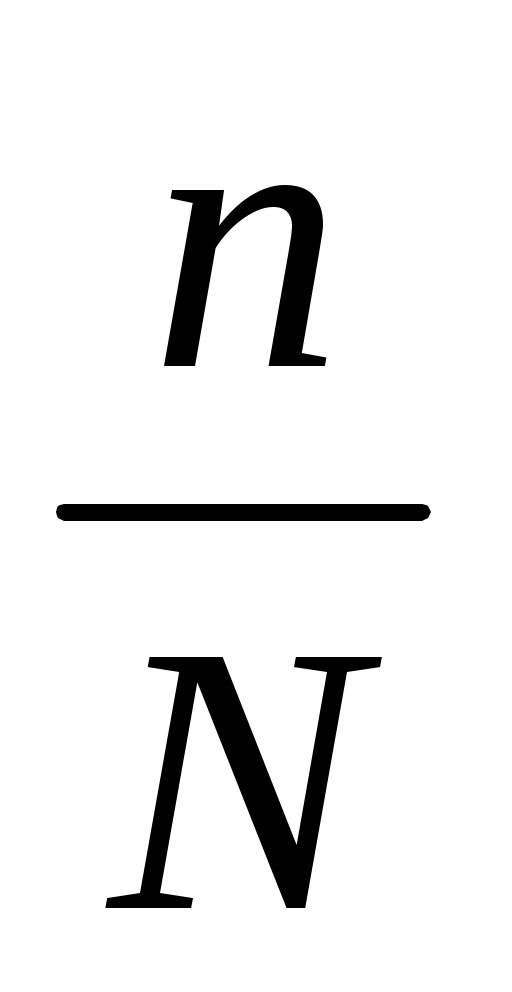 0,05. 0,05.
Более точное соотношение для средней ошибки выборки имеет вид:
Sx = 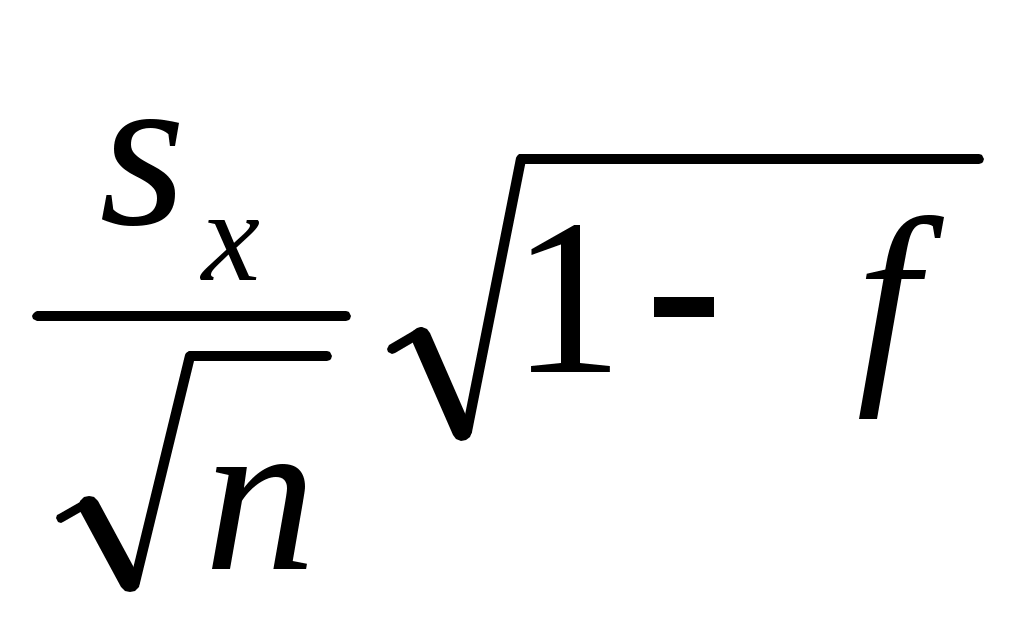 . .
При бесповторной выборке этого нельзя не учитывать.)
Отметим, что объем выборки может находиться только на основе известного генерального среднего квадратического отклонения (которую весьма нежелательно заменять на выборочную статистику Sx ).
Важно подчеркнуть, что для социолога может быть очень мало пользы от описанного способа определения объема выборки. Дело в том, что объём, определенный таким образом, позволяет обеспечить представительность выборки в отношении только одного признака (и только в отношении одной его характеристики – среднего арифметического значения; как было отмечено выше своя ошибка выборки имеется и у других параметров рассматриваемых распределений). Поэтому такой признак выступает в роли "главного" для исследователя. Конечно, можно было бы таким же образом определить объём, принимая во внимание любое количество признаков: найти много значений n и считать, что искомый объём должен быть равен максимальному из них. Но положение гораздо сложнее. Заранее, до сбора и анализа данных социолог обычно не имеет "в руках" того признака, который действительно можно считать "главным". Такого рода признаки обычно являются латентными, их значения находятся только в результате обработки некой первичной информации. И вопрос о том, какой должна быть выборка для сбора этой первичной информации, по существу остаётся открытым до проведения исследования.
6.3. Доверительный интервал для медианы.
Об ошибке выборки для медианы мы уже говорили при сравнении эффективности среднего арифметического и медианы как точечных оценок генерального математического ожидания. Распределение выборочных значений медиан является нормальным:
Ме выб
N (x, 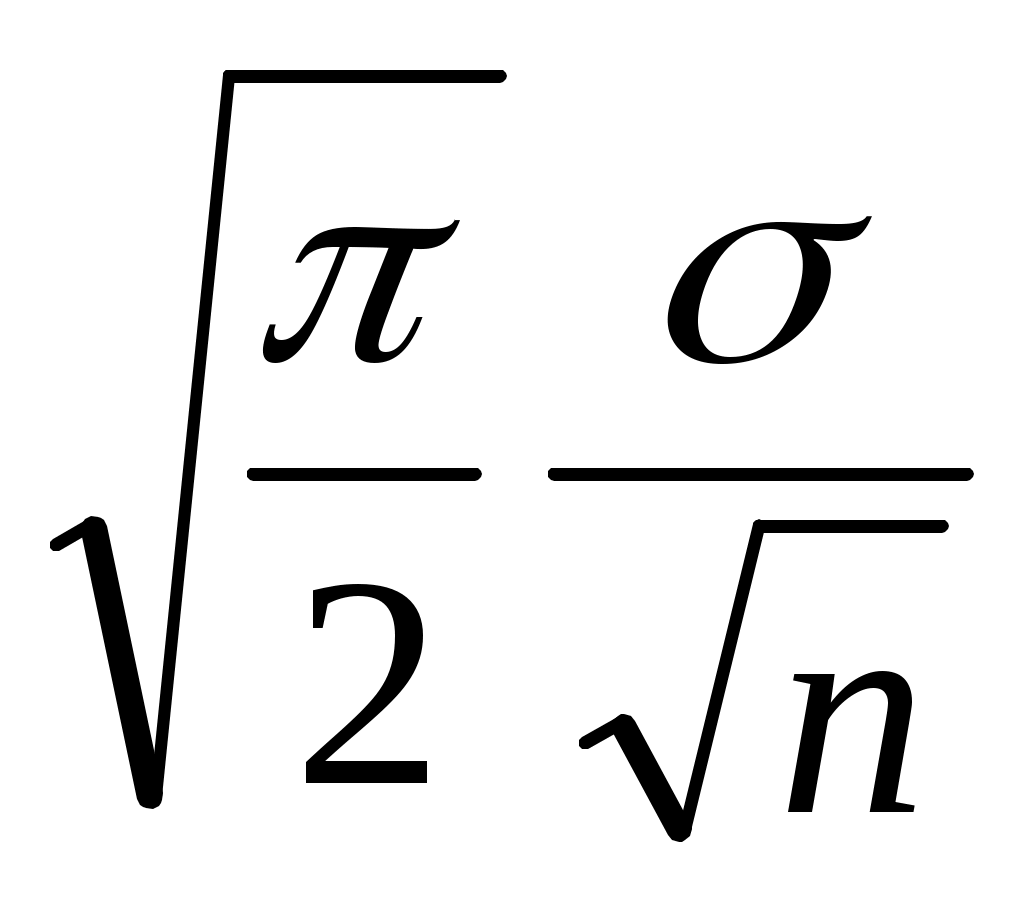 ). ).
Значит, в соответствии с описанными выше принципами, доверительный интервал для медианы выглядит следующим образом:
Ме выб - z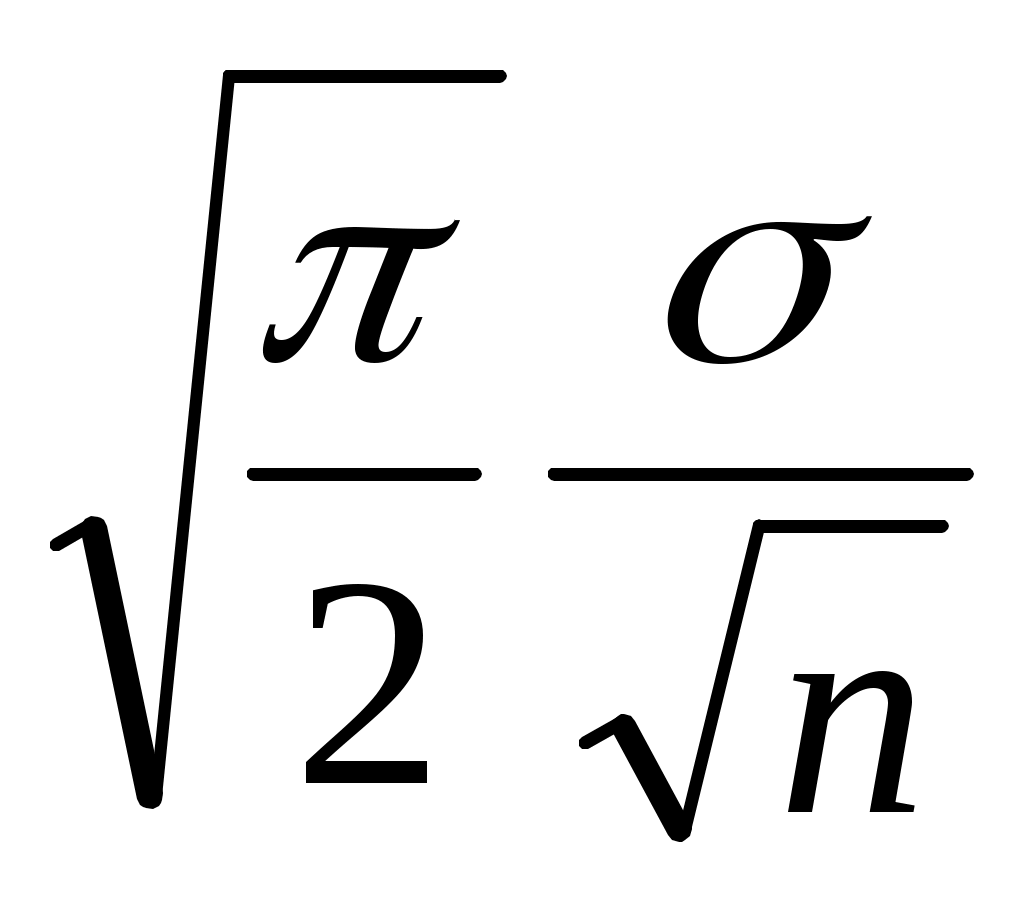 Ме ген Ме выб + z Ме ген Ме выб + z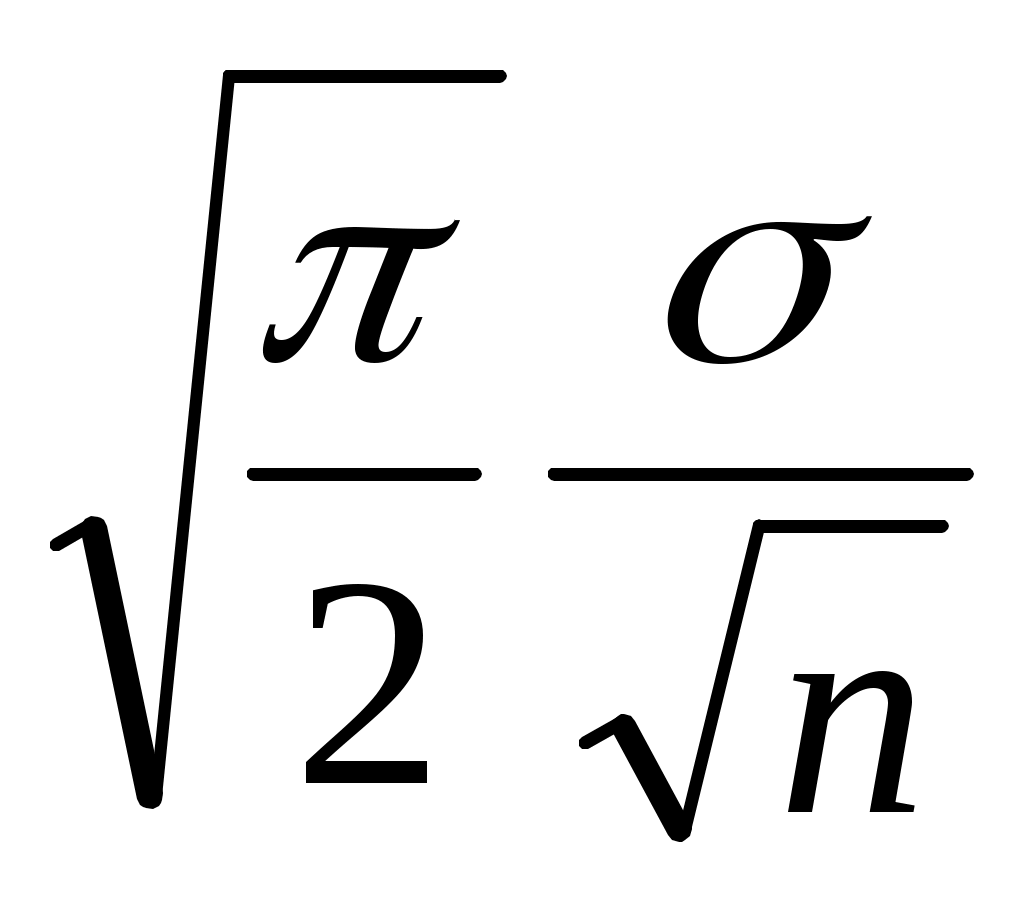 . .
Выражение = z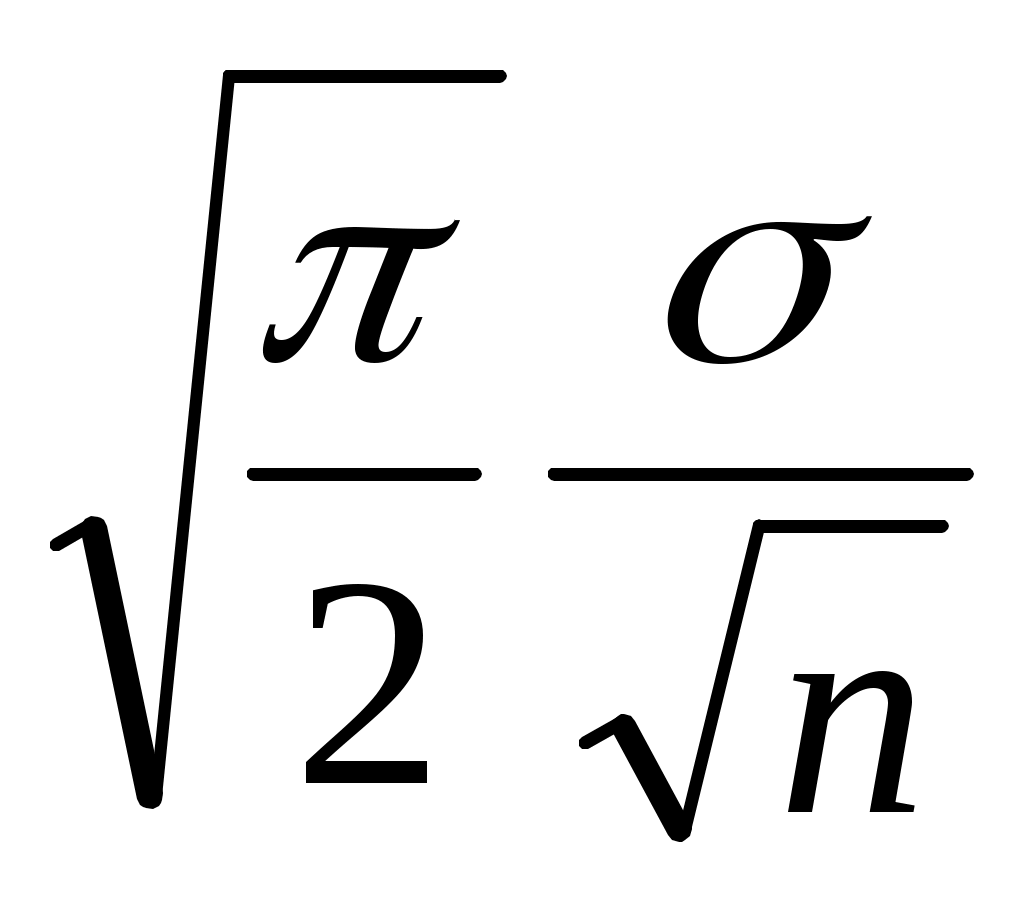 называется предельной ошибкой выборки для медианы, если оно представляет собой определенное из содержательных соображений максимально возможное (естественно, это выражение носит вероятностный характер, задается определенный уровень значимости , которому в формуле отвечает значение z) отклонение выборочных медиан от генеральной. называется предельной ошибкой выборки для медианы, если оно представляет собой определенное из содержательных соображений максимально возможное (естественно, это выражение носит вероятностный характер, задается определенный уровень значимости , которому в формуле отвечает значение z) отклонение выборочных медиан от генеральной.
Отметим, что правило, в соответствии с которым при отсутствии сведений о генеральной дисперсии мы заменяем на s , а если к тому же и объем выборки мал (не больше 30 единиц), то вместо z используем tn-1, действует при построении доверительного интервала для медианы так же, как и при построении аналогичного интервала для математического ожидания.
6.4. Доверительный интервал для доли
Доверительные интервалы могут быть построены отнюдь не только для генеральной средней и медианы, но и для многих других параметров распределений: дисперсии, коэффициента корреляции и т.д. Мы рассмотрим с соответствующей точки зрения ешё только одну статистику: долю встречаемости какого-либо значения одного из рассматриваемых признаков. Смысл соответствующей содержательной задачи представляется ясным. Представим, скажем, что доля мужчин в выборке оказалась равной 54%. Встает вопрос о какой-то оценке этой доля в генеральной совокупности. Как и выше, ответ на этот вопрос будет дан с помощью построения доверительного интервала для генеральной доли (т.е. – вероятности встречаемости свойства «быть мужчиной» среди объектов изучаемой генеральной совокупности).
Обозначения: p - упомянутая доля для выборки, - для генеральной совокупности, q = 1-p, sр - средняя ошибка выборки для доли p. Для любого уровня значимости можно найти такое z, что будет справедливым соотношение:
Р (р - р + ) = 1 - , где
= z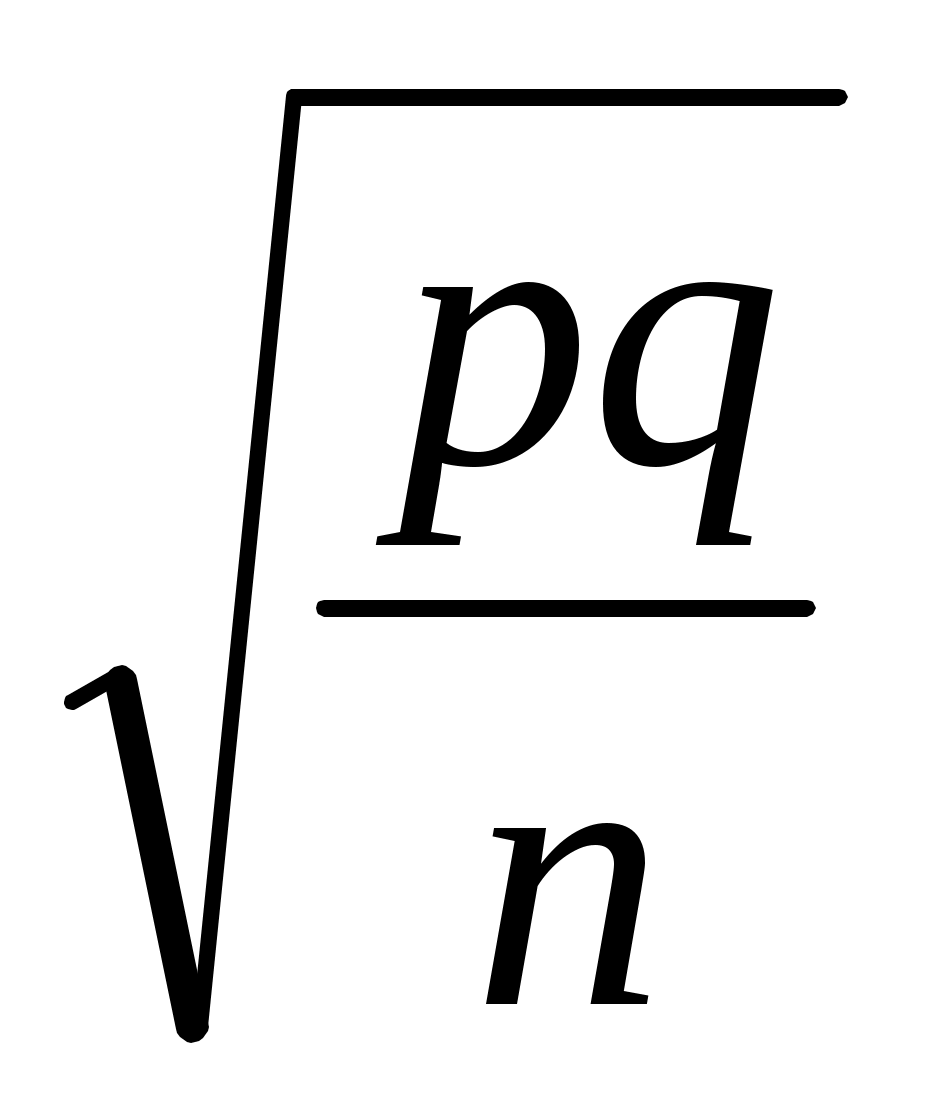 , т.е. , т.е.
Р (р - z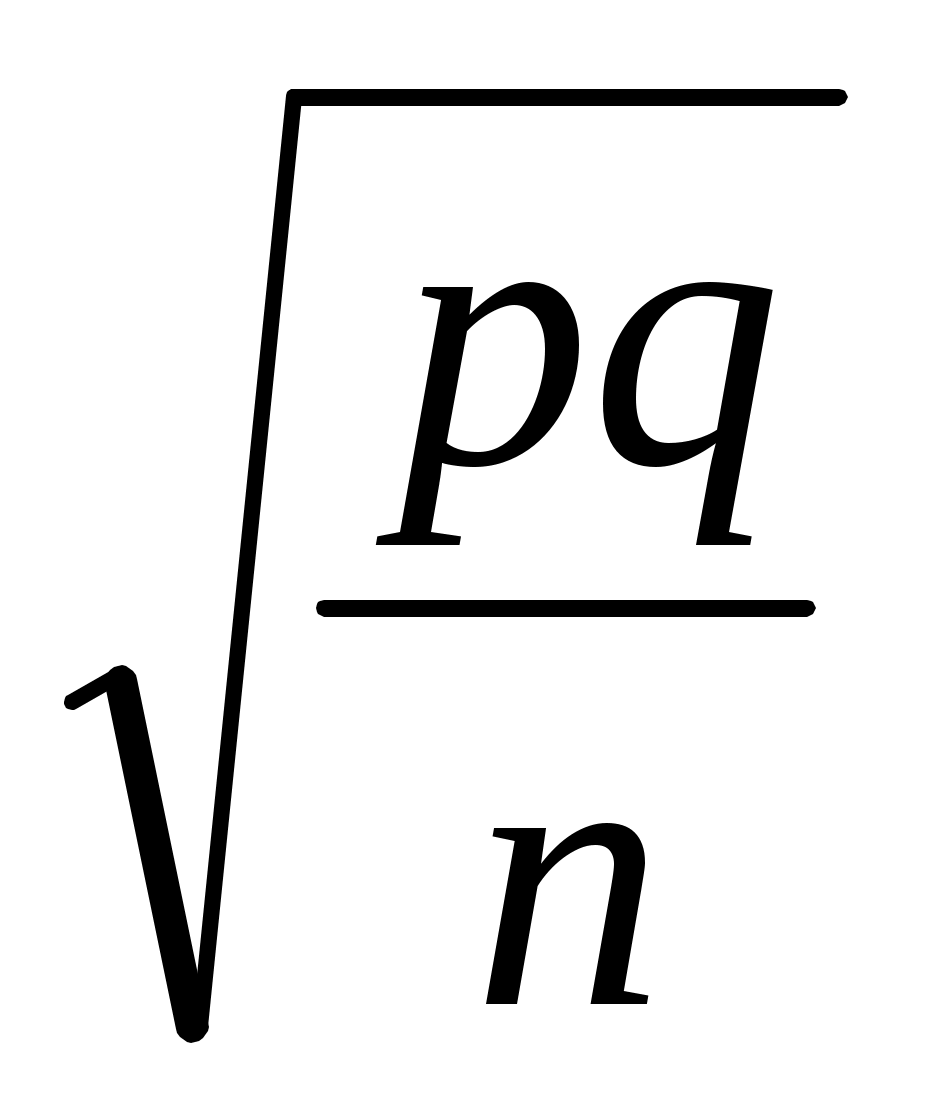 р + z р + z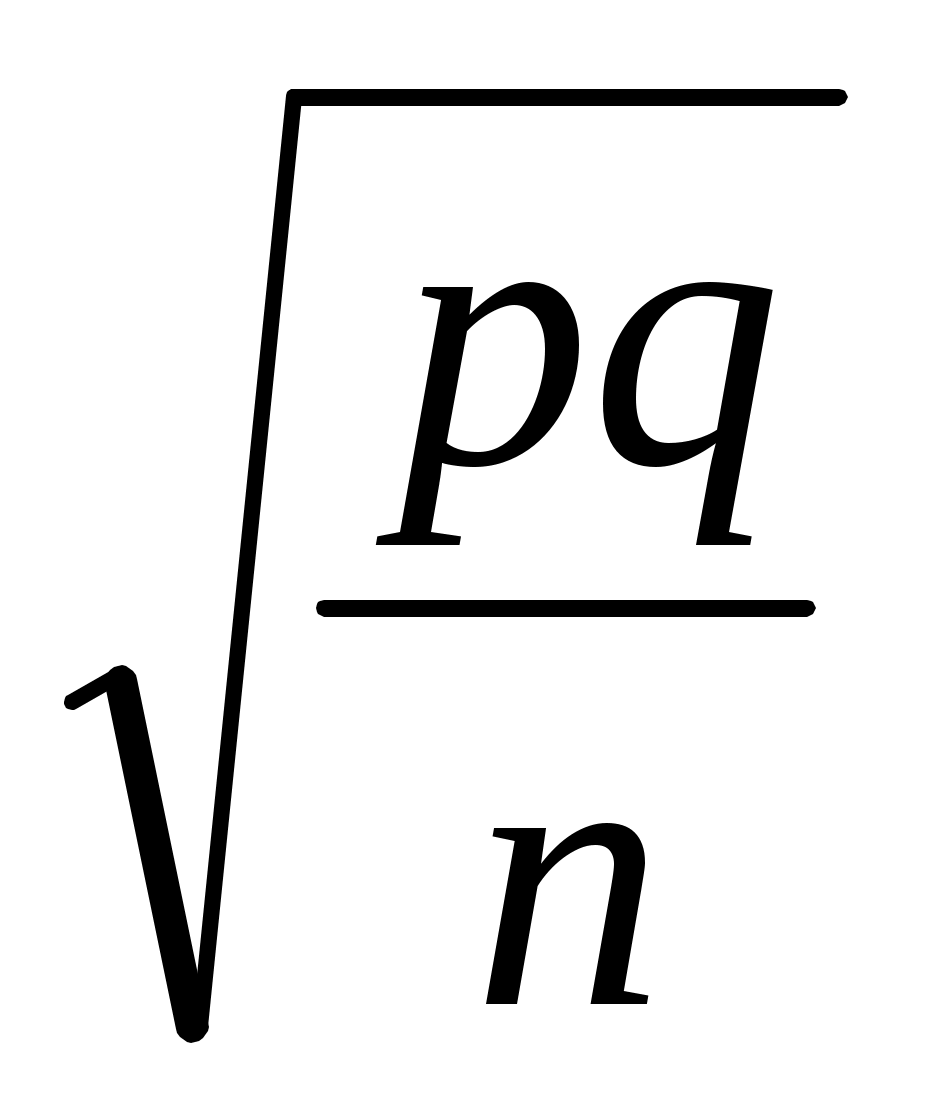 ) = 1 - (6) ) = 1 - (6)
Заметим, что величина Sр = 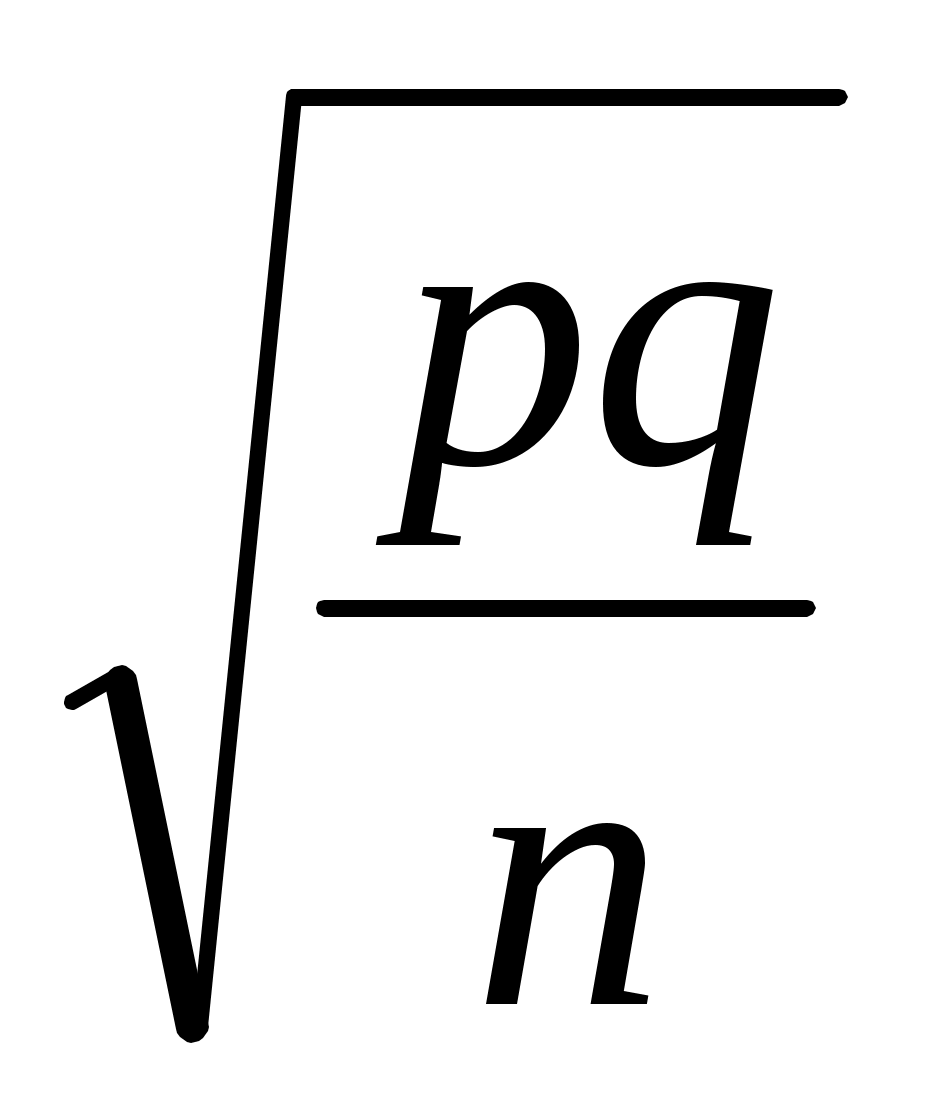 - это средняя ошибка выборки для доли p (т.е. средний разброс таких долей, вычисленных для всех мыслимых выборок). Если как-то удастся определить максимально возможную величину , то, по аналогии с соответствующими рассмотрениями выше, эта величина будет называться предельной ошибкой выборки для доли. - это средняя ошибка выборки для доли p (т.е. средний разброс таких долей, вычисленных для всех мыслимых выборок). Если как-то удастся определить максимально возможную величину , то, по аналогии с соответствующими рассмотрениями выше, эта величина будет называться предельной ошибкой выборки для доли.
Подчеркнем, что значения p и q обычно рассчитываются для выборки, хотя в идеале здесь тоже (как и в случае расчета доверительного интервала для математического ожидания) должны быть генеральные показатели.
Формула для вычисления Sр фактически совпадает с формулой для вычисления Sх при определенном взгляде на принятое во внимание значение рассматриваемого признака. Рассмотрим этот аспект более подробно, поскольку этот факт имеет довольно принципиальное значение для выработки подходов к анализу социологических данных..
6.5. Связь средних ошибок среднего арифметического и доли, обобщение этого факта на многомерный анализ
Предположим теперь, что выделенному значению «a» рассматриваемого признака (тому, доля встречаемости которого равна p; в приведенном выше примере значение «a» означает «мужчина») поставлен в соответствие некоторый специальным образом построенный номинальный дихотомический признак Y:
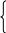
1, для респондентов, обладающих значением «a»,
Y= (6.7)
0, для остальных респондентов.
Можно показать, что формула (6.5) для такого признака превращается в формулу (6.6)
Этот факт, несмотря на свою очевидность, очень важен для социолога. Его можно обобщить и на этой основе открыть путь широкому использованию традиционных количественных математико-статистических методов для изучения номинальной информации. С этой целью осуществляют так называемую дихотомизацию номинальных данных: каждому значению номинального признака только что описанным способом ставят в соответствие дихотомический номинальный признак, принимающий два значения: 0 и 1 (таким образом вместо одного номинального признака, имеющего k значений, появляется k новых дихотомических признаков). Можно показать, что в результате применения традиционных «числовых» методов к такого рода признакам, получается нечто осмысленное, если определенным образом разумно интерпретировать результаты (так, результатом решения задачи 3, приведенной после лекции 2, должны получиться соотношения, говорящие о том, как можно разумно интерпретировать среднее арифметическое значение и дисперсию такого дихотомического признака: 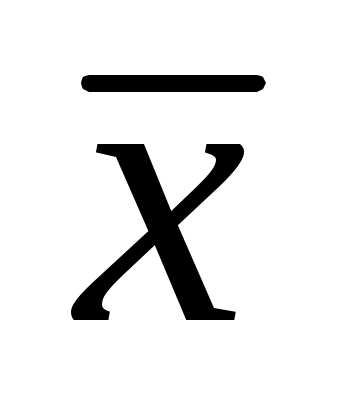 = p, Dx = pq, где p – доля единичных значений признака, а q – нулевых). Подобный подход широко используется в регрессионном анализе с фиктивными переменными (коими называются описанные выше дихотомические признаки), в логистической регрессии и т.д. Интерпретация коэффициентов уравнений регрессии при этом своеобразна, не похожа на то, что имеет место в классическом «числовом» случае. = p, Dx = pq, где p – доля единичных значений признака, а q – нулевых). Подобный подход широко используется в регрессионном анализе с фиктивными переменными (коими называются описанные выше дихотомические признаки), в логистической регрессии и т.д. Интерпретация коэффициентов уравнений регрессии при этом своеобразна, не похожа на то, что имеет место в классическом «числовом» случае.
Примеры задач.
Рекомендация. Если речь идет о выборе меры средней тенденции (для нас выбор ограничивается двумя средними - 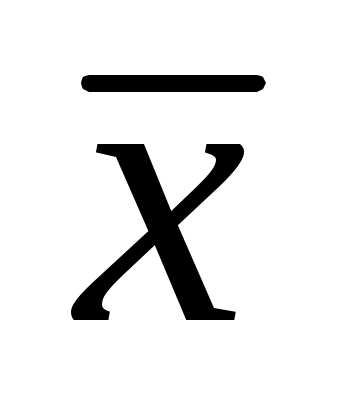 и Ме), то следует учитывать тип используемых шкал. и Ме), то следует учитывать тип используемых шкал.
Доказать, что для признака вида (7) формула (5) превращается в формулу (6)
Министерство образования намеревается с помощью специального теста оценить средний уровень профпригодности молодых социологов - выпускников профильных вузов. Некоторые предварительные исследования позволяют считать, что среднее квадратическое отклонение, характеризующее разброс значений теста, равно 3,5. Какого объема выборку надо использовать, если исследователи хотят, чтобы с вероятностью 97% найденное среднее не отклонялось от генерального более, чем на 1,5?
Респонденты некоторой выборочной совокупности следующим образом распределились по возрасту
Возрастной интервал
|
Количество респондентов, попавших в интервал
|
15-20
20-25
25-30
30-35
35-40
|
20
40
40
60
40
|
Найти 92%-й доверительный интервал для математического ожидания и 97%-й доверительный интервал для доли людей, попавших по возрасту в интервал (25-30) лет.
На основе изучения выборки из 100 абитуриентов, прошедших тестирование, был подсчитан средний балл. Он оказался равным 7,8. Известно, что = 2,0. Найти 93%-й доверительный интервал для генерального среднего.
10 случайно отобранных абитуриентов, поступающих в некоторый вуз, получили следующие баллы (использовалась интервальная шкала) на вступительных экзаменах:
5, 2, 1, 2, 3, 7, 5, 5, 6, 4.
Каков тот интервал, в котором с вероятностью 94% лежит генеральное математическое ожидание баллов, полученных всеми поступающими в вуз абитуриентами?
Предположим, что национальным меньшинством называется народность, составляющая менее 8% в общей совокупности жителей данной страны. В ходе выборочного опроса 2000 жителей страны 135 человек заявили, что являются бушменами. Можно ли с уверенностью 95% считать бушменов национальным меньшинством?
Респонденты некоторой выборочной совокупности были опрошены по шкале Лайкерта. Диапазон изменения установки был разбит на четыре интервала. Получилось следующее распределение.
Интервал изменения Количество респондентов, попавших
установки в интервал
10-15 50
15-20 20
20-25 40
25-30 40
Найти 96%-й доверительный интервал для медианы .
Результаты опроса некоторой совокупности респондентов по определенному тесту отражены в следующей таблице:
Значение теста
|
-2
|
1
|
2
|
3
|
4
|
5
|
Частота
|
2
|
1
|
2
|
2
|
2
|
1
|
Оценить с надежностью 0,95 математическое ожидание в соответствующей генеральной совокупности
Респонденты некоторой выборочной совокупности были опрошены по шкале Лайкерта. Диапазон изменения установки был разбит на четыре интервала. Получилось следующее распределение.
Интервал изменения Количество респондентов, попавших
установки в интервал
10-15 2
15-20 5
20-25 4
25-30 3
Найти 96%-й доверительный интервал для медианы .
Измеренная по шкале Лайкерта удовлетворенность 10-ти респондентов своей работой оказалась равной следующим величинам:
14, 10, 8, 21, 25, 21, 10, 16, 11, 10
Исследователь пока не определил, каков тип получившейся шкалы – порядковый или интервальный. Какие выводы мы можем сделать о средней удовлетворенности в генеральной совокупности в каждом из этих случаев ?
Раздел III. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
|
|
|
 Скачать 2.75 Mb.
Скачать 2.75 Mb.



 х - zx х
х - zx х 




 х - zx х х + zx
х - zx х х + zx 




 известна используем z
известна используем z