Математико-статист модели в социологии. Учебное пособие оглавление введение. В основная цель курса, адресат
 Скачать 2.75 Mb.
|
10.2. Проверка гипотезы о равенстве двух дисперсийВернемся к рассмотрению той статистической гипотезы, которую мы уже упомянули при обсуждением правил выбора критерия для проверки гипотезу о равенстве генеральных математических ожиданий - гипотезу о равенстве генеральных дисперсий: Н 0 : 12 = 22. Итак, предположим, что выборка объемом n1 случайно извлекается из нормальной совокупности со средним 1 и дисперсией 12. Независимая случайная выборка объемом n2 извлекается из второй нормальной совокупности со средним 2 и дисперсией 22. При проверке Н0 значения математических ожиданий несущественны. Критериальная статистика F = (s12 / s22) имеет распределение Фишера (в предположении справедливости нуль-гипотезы) со степенями свободы (n1 – 1) и (n2 – 1). В вероятностных таблицах для этого распределения, как правило, вверху указывается число степеней свободы для большей дисперсии, а слева – для меньшей (или вверху - число степеней свободы для числителя, а внизу – для знаменателя). По существу речь идет о проверке сходства степеней однородности двух выборок. Критерий может быть двусторонним, поскольку интересующее нас отклонение F от 1 может быть и в правую, и в левую сторону. Значит, альтернативная гипотеза может быть ненаправленной и направленной. Ненаправленная альтернативная гипотеза выглядит так: Н1 : 1 2. Критерий в таком случае – двусторонний. Находим /2 F(n1 – 1),(n2 – 1) по таблице (в таблице обычно дают только те значения критерия, которые больше 1) и 1-/2F(n1 – 1),(n2 – 1) = 1 / (/2 F(n1 – 1),(n2 – 1)). Нулевая гипотеза принимается, если F лежит между этими двумя табличными (критическими) значениями и отвергается в пользу ненаправленной Н1, если F выходит за пределы этого интервала, неважно в какую сторону- вправо, или влево. Направленные альтернативные гипотезы имеют вид: Н1 : 1 2 и Н1 : 1 2 . Логика их проверки – та же, что и логика проверки альтернативных гипотез, описанных выше. 10.3. Проверка гипотезы о равенстве нулю коэффициента корреляции В социологических исследованиях довольно часто возникает ситуация, когда исследователь не знает, как следует интерпретировать коэффициент корреляции, рассчитанный для измерения связи между двумя интервальными. Скажем, равен этот коэффициент 0,3. Какой вывод должен сделать исследователь – имеется связь между переменными или нет? И снова, как и выше, на помощью приходит проверка статистической гипотезы. 58 Рассмотрим способ проверки нуль-гипотезы - H0: = 0. Для такой проверки используется критерий  (напомним, что греческие буквы используются для обозначения генеральных параметров, а латинские – для отвечающих им выборочных статистик; в соответствии с этим r означает выборочный коэффициент корреляции). Эта статистика при справедливости нуль-гипотезы имеет распределение Стьюдента с df = (n – 2) степенями свободы. Альтернативная гипотеза Н1 в данном случае может быть ненаправленной и направленной (это естественно, если вспомнить, что коэффициент корреляции может быть и положительным, и отрицательным), а рассмотренный критерий, соответственно, двусторонним и односторонним. Направленный вариант альтернативной гипотезы - H1: 0 (или – H1: 0), ненаправленный - H1: 0. Подчеркнем, что при ненаправленной альтернативной гипотезе (и, соответственно, при использовании двустороннего критерия) гипотеза принимается, если - tтабл tнабл. tтабл., и отвергается, если tнабл выходит за пределы указанного интервала. 10.4. Проверка гипотезы о равенстве долейНередко в социологии возникает ситуация, когда требуется проверить гипотезу о равенстве генеральных долей: Н0:  .Имеются в виду доли тех единиц рассматриваемых совокупностей (выборочной и генеральной), которые обладают каким-то заданным свойством. К примеру, исследователь выяснил, что среди опрошенных им студентов социологических вузов оказалось 13% юношей, а среди студентов экономических вузов- 21%. Встает вопрос, является ли это расхождение случайным (может быть объяснено тем, что выборки не достаточно адекватно отразили свойства генеральных совокупностей – всех студентов социологических и экономических вузов Москвы соответственно) или же оно принципиально – в экономические вузы действительно поступает относительно больше юношей, чем в социологические. И снова для ответа требуется проверка статистической гипотезы.59 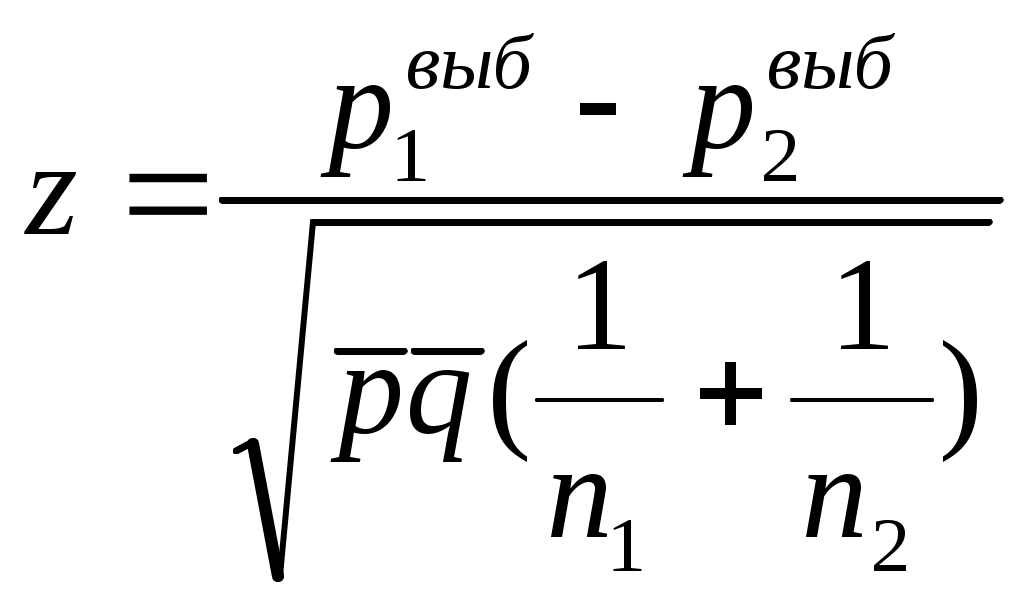 , где ,  , X1 – количество единиц первой выборки, обладающих рассматриваемым качеством, X2 – то же для второй выборки.Примеры задач. 1. Работая в одном из вузов, преподаватель убедился, что все его студенты являются достаточно однородными по уровню подготовки и разбиения отдельных учебных групп на подгруппы не требуется. Когда преподаватель решил начать работать в другом вузе, встал вопрос о том, следует ли группы этого вуза разбивать на однородные подгруппы. Чтобы быстро решить этот вопрос, преподаватель сформировал две выборки из студентов первого и второго вузов соответственно, составил специальный тест, с помощью которого опросил студентов обеих выборок. Было решено разбивать группы второго вуза, если разброс полученных по тесту оценок студентов второй выборки будет больше разброса аналогичных оценок студентов первой выборки и это различие будет статистически значимо.  Какое решение примет преподаватель, если в выборке из первого вуза было 30 студентов, из второго – 25, а выборочные дисперсии равны, соответственно, 2,5 и 3,0 ?2. Имеем следующую статистику по выборке из 5-ти регионов: № региона 1 2 3 4 5 Доля тяжких преступлений (на 1000 жителей) 0,05 0,01 0,2 0,08 0,9 Доля безработных (к численности работоспособ- ного населения) 0,02 0,0005 0,05 0,03 0,1 Можно ли считать, что преступность обусловлена уровнем безработицы? 3. При изучении электорального поведения населения часто возникает проблема определения того, за кандидата какой партии голосовали бы те избиратели, которые не пришли на голосование. Для доказательства того, что не пришли в основном сторонники партии А, было предложено подсчитать коэффициент корреляции между следующими наборами процентов:   № избирательного 1 2 3 4 5 6 7 участка % явившихся на 70 60 50 65 30 40 70 голосование % проголосовавших 25 20 15 21 10 15 20 за кандидата партии А Логика рассуждений была такова: если существует связь между двумя выписанными рядами процентов (т.е. с ростом процента явившихся растет процент проголосовавших за кандидата А), то имеет смысл полагать, что отсутствующие на голосовании действительно являются сторонниками партии А. Можно ли считать, что в рассматриваемом случае связь есть? 4. При составлении анкеты проверялась гипотеза о том, что ответ респондента на некий закрытый вопрос анкеты зависит от порядка расположения вариантов предлагаемых ответов. В частности, предполагалось, что в случае, когда определенный вариант будет назван первым, то респондент отметит его с большей вероятностью, чем в случае, когда он назван последним. Для проверки гипотезы было опрошено две схожих группы респондентов. В анкете, использованной при опросе первой группы, состоявшей из 20 человек, рассматриваемый вариант ответа шел первым и его отметили 12 человек. В анкете, использованной при опросе второй группы, состоявшей из 25 человек, тот же вариант шел последним, и его отметили 10 человек. Можно ли считать, что гипотеза подтвердилась? 5. Предполагалось, что о стабильности экономической обстановки в стране (отсутствии войн, стихийных бедствий и т.д.) за последние 50 лет можно судить по характеру распределения населения по возрасту: при спокойной обстановке оно должно быть равномерным. В результате проведенного исследования, для одной из стран были получены следующие данные.
Имеются ли основания полагать, что в стране была нестабильная обстановка? ТЕМА 11. |