Математико-статист модели в социологии. Учебное пособие оглавление введение. В основная цель курса, адресат
 Скачать 2.75 Mb. Скачать 2.75 Mb.
|
Повторение отдельных фрагментов курса по теории вероятностейФункция плотности одномерного распределения и функция распределения для одномерных непрерывных и дискретных распределений; связь этих функций друг с другом; основные параметры любого20 одномерного распределения - математическое ожидание, мода, медиана и другие квантили, дисперсия. Площадь под кривой функции плотности как оценка вероятности попадания значения случайной величины в соответствующий отрезок. Выборочное представление функции плотности распределения признака (непрерывного и дискретного): частотная таблица, полигон, гистограмма (в том числе с неравными интервалами). Различие стоящих за выбором полигона и гистограммы предположений о распределении признака внутри каждого интервала. Анализ моделей, заложенных в указанных способах выборочного представления случайной величины, их различие: при использовании полигона предполагаем, что все попавшие в интервал значения сосредоточены в одной точке (важно, что при построении графика на оси х может быть выбрана любая точка интервала, т.е. что выбор такой точки – тоже модельное предположение); при использовании гистограммы считаем, что распределение в каждом интервале равномерно; гистограмму имеет смысл рассчитывать только для непрерывного признака. Проблема построения выборочной функции плотности для непрерывного признака: разбиение диапазона изменения признака на интервалы, отнесение «стыка» соседних интервалов к одному из концов, пропущенные данные. Цели заполнения пропусков. Способы такого заполнения: средним арифметическим (может быть, с учетом значений других признаков) или другими средними (с учетом шкал, о шкалах пойдет речь в лекции 2), равномерно по всем градациям, пропорционально получившимся частотам. Модели, стоящие за каждым названным подходам к заполнению пропущенных значений. Выборочное представление функции распределения (кумулята): частотная таблица, полигон и гистограмма. Статистики, отвечающие основным параметрам одномерного распределения: среднее арифметическое, дисперсия, мода, медиана и другие квантили. Медиану необходимо уметь считать двумя способами: как середину вариационного ряда и с помощью кумуляты. То же для других квантилей. Снова обратить внимание на модель, заложенную в методе. Напомним основные формулы для расчета медианы и моды21. 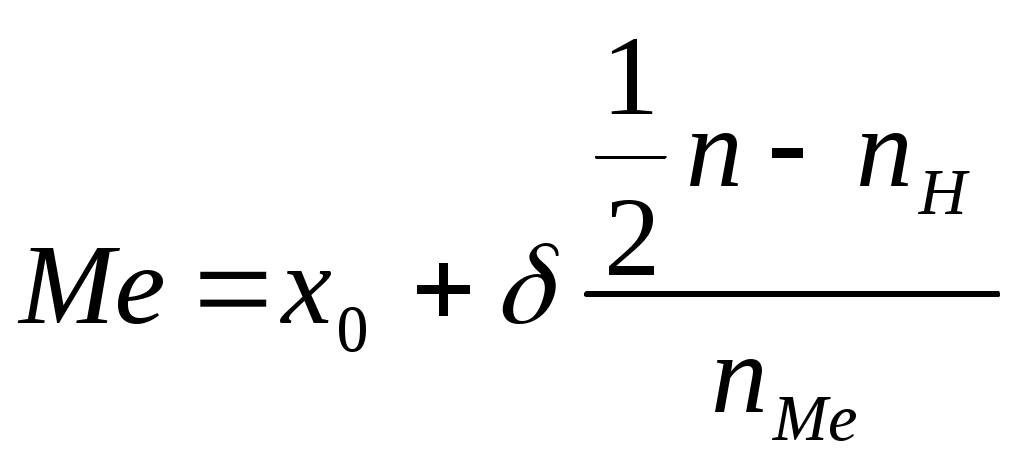 , ,где х0 – начало (нижняя граница) медианного интервала; - величина медианного интервала; n - объем выборки (или 100%, либо 1); nН – частота (или относительная частота в процентах, либо в долях), накопленная до медианного интервала; nМе – частота (или относительная частота в процентах, либо в долях) медианного интервала. 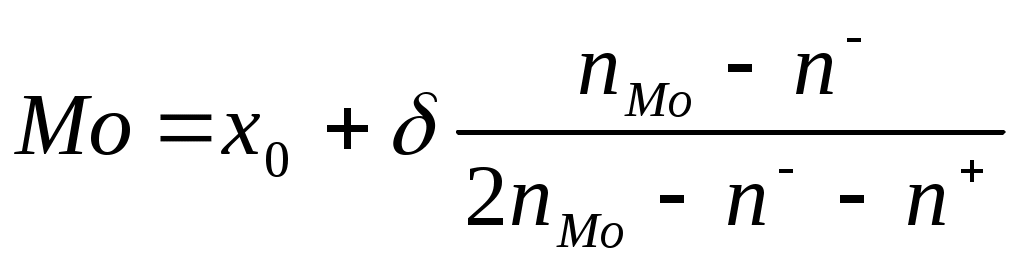 , ,где x0 – начало (нижняя граница) модального интервала; - величина модального интервала; nMo – частота модального интервала; n- - частота интервала, предшествующего модальному; n+ - частота интервала, следующего за модальным. Частоты, как и выше, везде могут быть заменены на относительные частоты, выраженные либо в процентах, либо в долях. Функция плотности и функция распределения двумерных случайных величин. Основной параметр двумерного распределения – коэффициент корреляции. Выборочное представление функции плотности двумерной случайной величины (частотная таблица, или таблица сопряженности). Маргинальные частоты, их связь с одномерными распределениями рассматриваемых признаков. Статистика, отвечающая генеральному коэффициенту корреляции. Напомним формулу для вычисления последней названной статистики. r = Кроме того, напомним важное свойство коэффициента корреляции: он измеряет только линейную связь. Это означает, что если он равен 1 или –1, то отвечающие нашим объектам точки рассматриваемого двумерного признакового пространства лежат на прямой линии, т.е. между признаками имеется точная линейная связь (прямая или обратная). А вот если r=0, то это означает не отсутствие связи вообще, а только отсутствие линейной связи. Нелинейная же связь при этом может быть и весьма сильной. Об этом мы будем говорить подробнее при обсуждении темы 13 (посвященной корреляционному отношению – коэффициенту, позволяющему измерить нелинейную связь). Понятие случайной выборки. Ее построение с помощью таблицы случайных чисел. Примеры задач. Придумать пример, демонстрирующий, что при разных разбиениях диапазона изменения непрерывного признака на интервалы можно получить качественно разные полигоны распределения – выборочные представлений функции плотности (разнокачественность распределений связать с пониманием описания данных как одной из задач науки). Примеры разнокачественных распределений: одновершинное и двухвершинное, одновершинное и равномерное, равномерное и с «ямой» и т.д. Задана следующая частотная таблица:
Простроить соответствующую гистограмму (заметим, что представленное в таблице разбиение диапазона изменения возраста на интервалы не лишено смысла; например, такое разбиение может явиться следствием особого внимания исследователя к тем периодам жизни человека, когда он вступает в трудовую жизнь (15-20 лет) и постепенно выходит из нее, готовясь к пенсии (5—55 лет для женщи5н). Описать, какие модели стоит за стандартными формулами расчета моды и медианы. Вспомнить геометрические правила расчета медианы с помощью выборочной функции распределения – кумуляты (в виде полигона). Показать, что эти правила приводят к тому же результату, что и соответствующая формула из п. 5 выше (раздел «Повторение отдельных фрагментов курса по теории вероятностей»). Разработать такой геометрический способ расчета моды с помощью выборочной функции плотности распределения (в виде гистограммы), который отвечал бы соответствующей формуле из п.5 выше. Составить формулы (аналогичные формуле для расчета медианы), позволяющие рассчитывать квартили, децили, процентили и другие возможные квантили. Показать, как эти формулы могут быть заменены геометрическими построениями на основе кумуляты. Предположим, что исследователя в первую очередь интересуют те возрастные категории, которые отвечают вхождению человека в работоспособный возраст (15-10 лет) и выходу из него (50-55 лет для женщин). Тогда естественным представляется разбиение диапазона изменения возраста на интервалы, представленные в следующей таблице:
Построить гистограмму, отвечающую отраженным в таблице данным. Обосновать теоретически выбранный способ построения. Рассчитать средние и дисперсию для доли явившихся на голосование жителей некоторого региона, если известны аналогичные доли для каждого из находящихся на территории региона участков. Данные представлены следующей таблицей:
Рассчитать коэффициент корреляции между стажем работника и его зарплатой на основе следующей частотной таблицы
У 12 школьников изучались две характеристики: оценки IQ, определенные с помощью шкалы интеллекта Стенфорда-Бине в шестом классе (Х) и успеваемость по химии в средней школе, оцененная на основе теста, состоящего из 35 вопросов (Y). Полученные данные отражены в следующей таблице: N 1 2 3 4 5 6 7 8 9 10 11 12  X 120 112 110 120 103 126 113 114 106 108 128 109  Y 31 25 19 24 17 28 18 20 16 15 27 19 Рассчитать коэффициент корреляции между Х и Y.  Показать, каким образом связаны выборочные формулы для расчета статистик: среднего арифметического, дисперсии, коэффициента корреляции для непрерывного признака – и известные формулы для расчета (с помощью интегралов) отвечающих этим статистикам генеральных параметров: математического ожидания, дисперсии, коэффициента корреляции. Показать, как выглядит функция плотности равномерного распределения и каким образом из нее с помощью интегрирования можно получить соответствующую функцию распределения. Как последняя выглядит? Осуществить с помощью таблицы случайных чисел выбор 5-ти студентов из группы. Добавочная литература к теме 1 . Обязательная (для повторения материала из курса по теории вероятностей: расчет выборочных статистик, отвечающих известным параметрам генеральных распределений) Толстова Ю.Н. Анализ социологических данных: методология, дескриптивная статистика, изучение связей между номинальными признаками. М.: Научный мир, 2000 Ниворожкина Л.И., Морозова З.А. Основы статистики с элементами теории вероятностей. Для экономистов. Ростов-на-Дону: Феникс, 1999 Рабочая книга социолога. М.: Наука, 1983 Дополнительная О методологических принципах использования математики в социологии Толстова Ю.Н. Методология математического анализа данных // Толстова Ю.Н. Социология и математика. М.: Научный мир, 2003. С.80-94. А также: СОЦИС, 1990, №6, с. 77-87. Проблемы пропущенных данных в массовых опросах Алгоритмы и программы восстановления зависимостей. - М.: Наука, 1984. Вапник В.Н. Восстановление зависимостей по эмпирическим данным. - М.: Наука, 1979. Загоруйко Н.Г. Эмпирическое предсказание. - Новосибирск: Наука, 1979. С. 105-118. Клюшина Н.А. Причины, вызывающие отказ от ответа // Социс (Социологические исследования). - 1990. - N1. С. 98-105. Лакутин О.В. Учёт пропущенных данных / Применение математических методов и ЭВМ в социологических исследованиях. - М.: ИСИ АН СССР, 1982. С.86-90. Лбов Г.С. Методы обработки разнотипных экспериментальных данных. - Новосибирск: Наука, 1981. С. 38-41, 52-55. Литтл Р.Дж., Рубин Д.Б. Статистический анализ данных с пропусками. - М.: Финансы и статистика, 1991. Фёдоров И.В. Причины пропуска ответа при анкетном опросе // Социс. - 1982. - N 2. Проблемы разбиения диапазона изменения признака на интервалы Орлов А.И. Асимптотика квантований и выбор числа градаций в социологических анкетах / Математические методы и модели в социологии. - М.: ИСИ АН СССР, 1977. С.42-55. Пасхавер Б. Проблема интервалов в группировках // Вестник статистики. - 1972. - N 6. Сиськов В.И. Об определении величины интервалов при группировках // Вестник статистики. - 1971. - N 12. А.А.Чупров. О приемах группировки статистических наблюдений // Известия Санкт-Петербургского политехнического института. 1904. Т. 1. Вып. 1–2. Doane D.P. Aesthetic frequency classification. American Statistician, 30, 1976. P. 181-183. Freedman D., Diaconis P. On this histogram as a density estimator: L2 theory. Zeit. Wahr. Ver. Geb.,57, 1981. P.453-476. Scott D.W. On optimal and data-based histograms. Biometrika, 66, 1979. P. 605-610. Scott D.W. Multivariate density estimation: theory, practice, and visualization. N.-Y.: John Wiley Sons, 1992. Sturges H. The choice of a class-interval. J.Amer. Statist. Assoc., 21, 1926. P.65-66. Wand M.P. Data-based choice of histogram bin-width. Technical report, Australian Graduate Scool of management, university of NSW. 1995. ТЕМА2. Общее представление о социологических шкалах. 1. Общие принципы понимания измерения в социологии Как мы уже отмечали во Введении, социолог не может отвлечься от проблемы измерения используемых им признаков. Напомним основные принципы теории измерений. Используемые ниже сокращения: ЭС – эмпирическая система, МС – математическая система, ЧС – числовая система. ЭС – это совокупность изучаемых объектов (например, в качестве таковой может служить множество студентов ГУ-ВШЭ), рассматриваемых как носители интересующих исследователя свойств (например, студенты могут интересовать исследователя как носители определенных политических взглядов). МС – это совокупность математических объектов, в которую ЭС отображается при измерении (в частности, ЭС может отображаться в ЧС). Итак, измерение – это отображение ЭС в МС: Э  С МС. С МС.И отображение это должно быть таким, чтобы у нас была гарантия адекватности «перехода» интересующих нас отношений между эмпирическими объектами в соответствующие им математические отношения между объектами МС. Так, если студенты интересуют исследователя лишь с точки зрения того, в какой степени каждый из них склонен к демократии, а рассматриваемая МС – числовая, то от чисел требуется, чтобы студенту с большей склонностью отвечало бы большее число. Чаще всего в качестве МС выступает ЧС. Тогда алгоритм, отображающий ЭС в МС, называется шкалой, соответствующий процесс измерения – шкалированием, а совокупность чисел, в которую мы отобразили элементы ЭС – шкальными значениями. Отметим, что нередко в социологии используются и нечисловые МС (например, граф, использующийся при изучении малой группы). Подчеркнем, что и ЭС, и МС – модели. Элементы ЭС – это не полноценные люди, а определенные «срезы» с них. Скажем, если студенты интересуют социолога как носители политических взглядов, то социологу должно быть безразлично, каков у них цвет волос (но только не в том случае, если вдруг окажется что блондины, скажем, более склонны к демократии, чем брюнеты). Элементы ЧС – не полноценные числа, а тоже лишь некоторые «срезы» с тех чисел, к которым мы привыкли в школе. Например, если в описанной выше ситуации с изучением политических взглядов студентов нас интересует только то, о чем шла речь, т.е. только сравнение студентов друг с другом по степени их склонности к демократии, то для нас будет осмыслен порядок получающихся чисел, но, скажем, соотношение 5-4=3-2 в таком случае не будет иметь смысла. 2.2. Определение номинальной, порядковой, интервальной шкалы Из-за того, что при шкалировании используются не все обычные свойства чисел, рассматриваемых в качестве шкальных значений, совокупность таких значений оказывается определенной не однозначно. Так, если мы отображаем лишь степень склонности студентов к демократии, то соответствующая эмпирическая упорядоченность с одинаковым успехом отобразится и в числах 2, 18, 19, и в числах 128, 154, 2037. То преобразование, с точностью до которого определена совокупность шкальных значений каких-либо элементов рассматриваемой ЭС, называется допустимым преобразованием шкалы. Тип шкалы определяется тем, какая совокупность допустимых преобразований этой шкале отвечает. Содержание таблицы 2 позволяет понять, каким образом определяются наиболее распространенные в социологии типы шкал - номинальная, порядковая, интервальная).
Таблица 2. Определение основных типов шкал Одна шкала называется шкалой более высокого типа, чем другая, если совокупность допустимых преобразований первой шкалы включается в совокупность допустимых преобразований второй. Среди шкал, из таблицы 2 наиболее высокий тип имеет интервальная шкала, наиболее низкий – номинальная. Результаты измерения по шкале более высокого типа больше похожи на числа. Определение типа шкалы нужно нам не для «красоты». То, по какой шкале получены исходные данные, определяет, каким образом эти данные можно анализировать для получения нового знания. Интуитивно ясно, что далеко не все операции осмыслены для шкал любого типа. Скажем, если мы используем номинальную шкалу для измерения национальности и приписываем первому респонденту, русскому, 1, второму – татарину – 2, третьему, украинцу – 3, четвертому, чукче, - 4, то вряд ли будем считать имеющим смысл выражение: Как же определить, чтó именно мы имеем право делать с числами, полученными по той или иной шкале? В некоторых книгах ответ на этот вопрос дается путем перечня ряда методов, отвечающих определенным шкалам: для интервальной шкалы мы имеем право считать среднее арифметическое, моду и медиану; для порядковой – моду и медиану; для номинальной – только моду и т.д. Но такой подход вряд ли может считаться удовлетворительным. Во-первых, для всех методов перечня не составишь. И даже если это удастся сделать сегодня, то что делать с теми методами, которые будут изобретены завтра? Во-вторых, совершенно не ясно, что означает «разрешение» использовать метод. Ну, скажем, то, что среднее арифметическое нельзя использовать так, как мы это сделали в приведенном выше примере, ясно уже на уровне здравого смысла. А почему его нельзя использовать для порядковых шкал? А как определить, можно или нельзя использовать для номинальных шкал, скажем, регрессионный анализ? Ответ уже не столь очевиден. В-третьих, приведенный выше перечень, вообще говоря, неверен. Так, бывают случаи, когда среднее арифметическое можно использовать и для номинальных данных. Пусть, скажем, мы измерили пол: мужчинам приписали 1, а женщинам - 0. Для 10 человек получили последовательность: 0, 0, 1, 0, 1, 0, 0, 1, 1, 0. Нетрудно видеть, что соответствующее среднее арифметическое будет равно 0,4. Если мы будем интерпретировать это обстоятельство так, как это обычно делается (наиболее типичный представитель рассматриваемой совокупности людей имеет пол 0,4), но, конечно, получим ерунду. Но попытаемся дать другую интерпретацию: доля единичных значений нашего признака в изучаемой совокупности составляет 40%. Вряд ли кто-нибудь будет возражать против того, что такая интерпретация вполне допустима. Так почему бы не считать среднее арифметическое для пола? Интерпретировать надо адекватно, и все будет в порядке. Для решения поставленных вопросов в теории измерений был разработан специальный подход. 2.3. Проблема адекватности математического метода. Интуитивно ясно, что, чем выше тип шкалы, тем более широкий круг методов применим для анализа соответствующих шкальных значений. Так, совершенно ясно, что к числам, полученным по номинальной шкале, многие традиционные математико-статистические методы не применимы. Это легко понять, рассмотрев две возможные номинальные шкалы из третьего столбца таблицы 2. Ясно, что, вообще говоря, очень многие методы будут давать разные результаты в зависимости от того, проанализируем ли мы с помощью выбранного метода числа (5, 5, 10, 185, 15) или же числа (25, 25, 3, 30, 1). Сравним, к примеру, средние арифметические значения первых трех объектов и последних двух объектов для каждой из номинальных шкал, приведенных в третьем столбце таблицы 2. Делаем содержательный вывод: первое среднее меньше второго. Проделаем то же для второй шкалы. Делаем противоположный вывод: первое среднее больше второго. А ведь если мы используем номинальную шкалу, то два рассмотренных набора шкальных значений содержат абсолютно одинаковую информацию! Значит, и результаты нашего анализа этих наборов должны быть одинаковыми. Естественно, у нас могут зародиться сомнения в целесообразности использования среднего арифметического для сравнения средних уровней двух рассматриваемых групп объектов. Существуют ли методы, результаты применения которых не зависят от того, какую из двух рассмотренных шкал мы выберем? Конечно. Этому условию будут удовлетворять все методы, опирающиеся на подсчет частот. Скажем, модальным значением в первом случае будет то, которым обладают первый и второй объект (скажем, если цифрой 5 закодирована национальность «татарин», то в рассматриваемом случае татар у нас – больше всего). То же – и во втором случае (снова «татар» у нас больше всего). Выводы не изменились. И вроде бы нет причин считать моду неподходящей статистикой для номинальной шкалы. Напротив, для интервальной шкалы большинство методов применимо. Попробуем, например, решить ту же задачу по сравнению средних для первых трех объектов и последних двух объектов для каждой из интервальных шкал, приведенных в третьем столбце таблицы 2. Для первой шкалы имеет место: Другими словами, наш содержательный вывод состоит в том, что первое среднее меньше второго. Теперь попробуем проделать то же для второй интервальной шкалы из третьего столбца таблицы. Вывод – тот же. Рассмотренный пример не дает оснований для возникновения сомнений в допустимости сравнения средних арифметических для интервальной шкалы. Разумно полагать, что аналогичные соображения будут справедливы и насчет моды. Более того, интуитивно ясно, методы, подходящие для номинальной шкалы, будут подходить и для интервальной. Все сказанное не случайно. Попытаемся выразить те же соображения в более строгом виде Математический метод называется формально адекватным, если результаты его применения не зависят от применения к исходным данным допустимых преобразований тех шкал, по которым эти данные получены. Если использовать это определение, то становится ясным, почему нельзя использовать среднее арифметическое для национальностей. Мы показали, что сравнение двух средних арифметических формально не адекватно относительно номинальных шкал. Покажем теперь, почему с формальной точки зрения нельзя рассчитывать средние для номинальной шкалы. Вернемся к обсужденному выше примеру. Напомним, что полученный содержательный вывод звучал так: «среднее между русским и украинцем равно татарину». Смысл этого утверждения изменится, если мы применим к набору исходных шкальных значений, скажем, следующее допустимое (для номинальной шкалы) преобразование: русским будем ставить в соответствие число 12, татарам – 5, украинцам – 10, чукчам – 11. Тогда среднее между русским и украинцем будет равно Напротив, наш результат, полученный с помощью расчета среднего арифметического для дихотомической шкалы, использованной нами при измерении пола, останется неизменным, если мы будем правильно его формулировать. А формулировку возьмем такую: среднее арифметическое делит интервал между числом, соответствующим женщине, и числом, соответствующим мужчине, в отношении 4:6 (что имело место выше и что по существу и говорило о доле единичных значений, равной 0,4). Покажем неизменность этого отношения на примере. Перекодируем произвольным образом значения пола: мужчинам припишем значение 48, а женщинам – 40. Нетрудно проверить, что тогда совокупность наших десяти шкальных значений превратиться в 40, 40, 48, 40, 48, 40, 40, 48, 48, 40, а среднее арифметическое будет равно 43,2, и будет верно соотношение: Поясним, почему выше мы дали определение не просто адекватности метода, а формальной адекватности. Дело в том, что формальная адекватность того или иного метода еще не делает его подходящим для решения социологической задачи соответствующего плана. Требуется еще другая адекватность, которую можно назвать содержательной – соответствие заложенной в методе модели сути решаемой задачи, априорным гипотезам исследователя (так, при осуществлении классификации объектов задействованная в алгоритме функция расстояния может быть формально адекватна типу используемых шкал, но содержательно совершенно не отвечать представлениям исследователя о похожести классифицируемых объектов). Примеры задач. Показать, что соотношение является инвариантным относительно допустимых преобразований интервальных шкал и не является таковым относительно допустимых преобразования порядковых шкал. На основе соответствующих рассуждений объяснить, почему нельзя усреднять результаты ранжировок респондентами каких-либо объектов с целью получения оценочных шкал (оценочная шкала – это процесс приписывания рассматриваемым объектам чисел, отражающих усредненное отношение к этим объектам всей совокупности респондентов). Рекомендация. Допустимые преобразования используемой шкалы должны быть одними и теми же для рассматриваемых шкальных значений. В данном случае – и тех, для которых рассчитывается Доказать, что значение коэффициента корреляции не изменится, если к исходным данным применить допустимое преобразование интервальных шкал. Предположим, что мы имеем совокупность значений номинального признака Х с двумя значениями 0 и 1. Пусть p – доля “1”, q – доля “0”. Выразить Описать, какова разница интерпретаций чисел 2, 3, 7 в ситуациях, когда эти числа получены по номинальной, порядковой или интервальной шкале. Доказать формальную адекватность моды (в любом контексте ее использования) для номинальной шкалы Доказать формальную адекватность рангового коэффициента корреляции (Спирмена или Кендалла) для порядковой шкалы. Добавочная литература к теме 2Обязательная Толстова Ю.Н. Измерение в социологии. М.: Инфра-М, 1998 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
