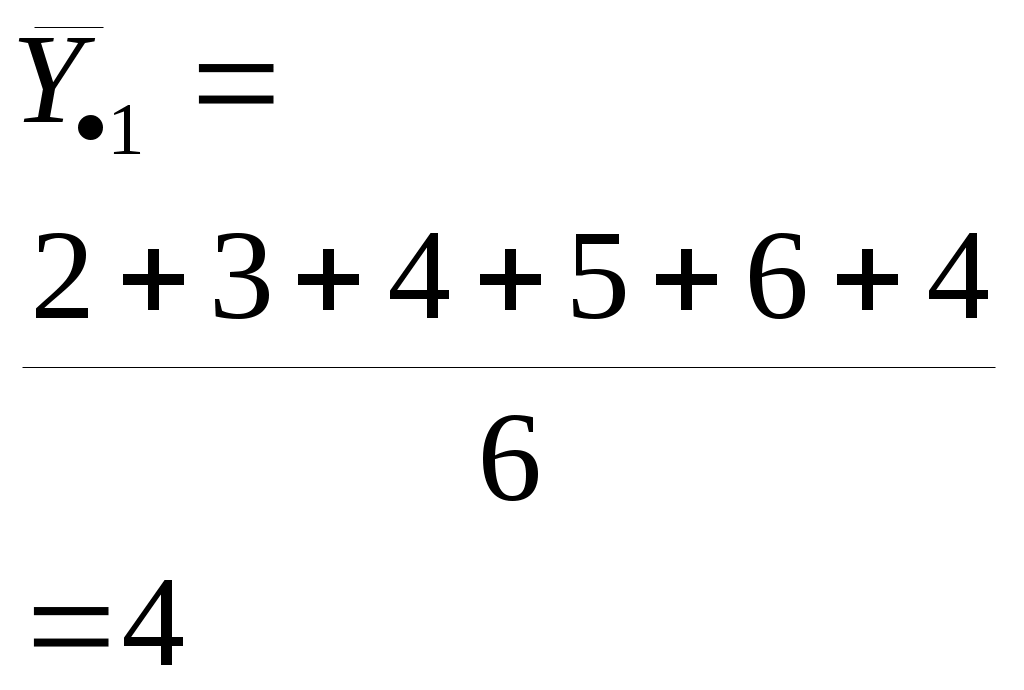Математико-статист модели в социологии. Учебное пособие оглавление введение. В основная цель курса, адресат

• Название: Учебное пособие оглавление введение. В основная цель курса, адресат
• Дата: 28.10.2022
• Размер: 2.75 Mb.
• Имя файла: Математико-статист модели в социологии.doc
• Тип: Учебное пособие; #760146
• страница: 13 из 17

ТЕМА 15

Двухфакторный дисперсионный анализ.

15.1. Двухфакторный дисперсионный анализ как метод анализа результатов эксперимента при изучении причинно-следственных отношений
Предположим, что решая рассмотренную выше задачу - выявление зависимости (независимости) успехов студентов от формы обучения, мы пришли к выводу о неполноте такой постановки задачи: к примеру, поняли, что эффективность формы обучения зависит от пола студента. Исходная матрица ячеек становится двумерной. Покажем, как она строится.

Пусть величина Y_ijk означает значение главного интересующего нас признака Y, вычисленное для i-го по счету (счет ведется внутри ячейки) объекта, помещенного в ячейку с номером ( j, k), где j – отвечающее рассматриваемой ячейке значение первого фактора X¹ , а k – отвечающее той же ячейке значение второго фактора X² .

Будем рассматривать упрощенный случай, когда число объектов во всех ячейках одинаково и равно n (в приведенной ниже таблице n = 3). Фактор X¹ - значения 1, 2, …, J (в примере J=2), а фактор X² принимает значения 1, 2, …, K (в нашем примере K = 3) .

Уровень фактора X1	Уровень фактора X2			Числ-ть Групп, отв-х уровням X1	Cреднее арифметическое значение Y для фиксированного уровня фактора X1
	1	2	3
1	Y111=2, Y211=3, Y311=4	Y112= 1 Y212=9 Y312=4	Y113=2 Y213= 4 Y313 =4	n1=nI=33=9
2	Y121=5, Y221=6, Y321=4	Y122=3 Y222=4 Y322=4	Y123=8, Y223=9, Y323=7	n2=nI=33=9	2 =5,6
Числ-ть Групп, отв-х уровням X2	=nJ=32=6	n ·2=nJ= =32=6	n3=nJ= =32=6	n=n= 18
			3= 5,6		= 4,6

1. 
   Модель двухфакторного дисперсионного анализа
   

Общая модель двухфакторного дисперсионного анализа имеет вид:

,

где

- - значение зависимого признака для конкретного респондента, помещенного в ячейку, отвечающую j – му уровню первого фактора и k – му уровню второго фактора (скажем, обучающемуся по второй форме юноши, тогда j=2, k=1), имеющему номер i в соответствующей ячейке;

- - вклад j-го уровня (нижний индекс) первого фактора (верхний индекс) X¹ в формирование значения Y (в нашем примере первый фактор – форма обучения; упомянутый вклад определяется тем, что студент обучался либо по первой форме обучения (j=1), либо по второй (j=2), либо по третьей (j=3));

- - вклад k-го уровня второго фактора X² в формирование значения Y (в нашем примере второй фактор – пол студента; соответствующий вклад определяется тем, является ли студент юношей или девушкой);

- - вклад, определяющийся взаимодействием i-го уровня первого фактора и j-го уровня второго;

• 
  _{I j k} – поправочный коэффициент (остаточный член), говорящий о различии между реальным значением Y-ка для рассматриваемого респондента и тем его значением, которое должно получиться для любого респондента, вошедшего в рассматриваемую ячейку (с номером (j,k)) в соответствии с нашей моделью.
  

Особое внимание стоит уделить понятию взаимодействия. Именно наличием этого элемента принципиально отличается двухфакторный дисперсионный анализ от однофакторного. Наличие взаимодействия двух признаков (в отношении некоторого зависимого признака Y) говорит о том, что вид связи первого признака с Y зависит от того, какое значение принимает второй признак. К примеру, по отдельности и форма обучения, и пол могут в среднем (статистически) не влиять на качество обучения, но, скажем, вторая форма обучения применительно к девушкам при этом может давать очень высокий положительный эффект. Другими словами, действие формы обучения зависит от того, для девушек или для юношей она используется. Когда в принципе уровень Y-ка зависит от сочетаний конкретных значений X¹ и X² , говорят о наличии взаимодействия между рассматриваемыми факторами. Иногда в том же смысле говорят о синергетическом эффекте, вызванном сочетанием значений факторов. В том же смысле ведут речь о нелинейности воздействия факторов на зависимую переменную. Иногда взаимодействием называют само сочетание значений факторов, обусловливающее некий конкретный уровень Y-ка.¹⁰¹
Выборочные оценки всех формирующих модель составляющих вычисляются аналогично тому, как это делалось для однофакторного дисперсионного анализа.

Название элемента модели	Обозначение	Выборочная оценка
Общий средний уровень		
Вклад j-го уровня фактора Х1		j - 
Вклад k-го уровня фактора X2		k - 
Вклад, определяющийся взаимодействием i-го уровня фактора X1 и j-го уровня фактора X2;		jk - j - k + 
Остаточный член	I j k	Yijk- jk

Определенную сложность представляет лишь оценка взаимодействия. Зададимся вопросом о том, каким образом можно оценить наличие (или отсутствие) взаимодействия в конкретной ячейке с номером (j,k). Наличие некоего среднего уровня, совокупное воздействие j-го уровня фактора X¹ и k-го уровня фактора X² в отдельности вкупе с взаимодействием указанных уровней приводят к тому, что средний уровень успеваемости для объектов рассматриваемой ячейки оказывается равным _jk. Он состоит из общего среднего уровня _, вклада j-го уровня первого фактора ( _j - _), вклада k-го уровня второго фактора ( _k - _) и вклада упомянутого взаимодействия. Как же получить оценку последнего. Естественно, путем «вытаскивания» из среднего уровня, типичного для рассматриваемой ячейки, названных вкладов. Другими словами, выборочная оценка взаимодействия равна
_jk- ( _j - _) - ( _k - _) = _jk - _j - _k + _. (15.1)
Аналогичные рассуждения справедливы и для генеральной совокупности. Этим мы воспользуемся в следующем параграфе при обсуждении вида гипотез, проверяемых в двухфакторном дисперсионном анализе.

15.3. Двухфакторный дисперсионный анализ как проверка статистических гипотез