Усольцев А.А. Векторное управление асинхронными двигателями. Учебное пособие по дисциплинам электромеханического цикла СанктПетербург 2002 Содержание
 Скачать 497 Kb. Скачать 497 Kb.
|
|
2.4.2. Преобразователи числа фаз 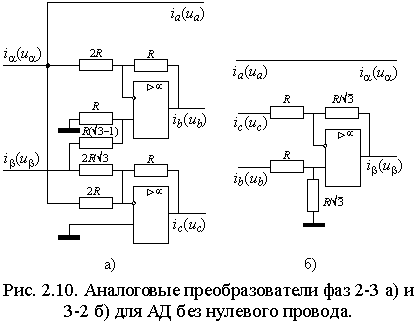 Если АД имеет трехфазную обмотку статора, то его структурная схема содержит внутренний преобразователь числа фаз (ПФ 3-2 на рис. 2.6), реализующий преобразование в соответствии с выражениями (1.1.3) для токов или напряжений статора. В этом случае УМ также должен быть трехфазным, а его вход должен подключаться к выходу УУ через преобразователь (ПФ 2-3 на рис. 2.6) с обратной передаточной функцией, т.е. соответствующей выражениям (1.1.2). Пример реализации такого преобразователя на основе операционных усилителей показан на рис. 2.10 а). В цифровых системах управления преобразование числа фаз осуществляется реализацией функций (1.1.2) и (1.1.3) . 2.4.3. Вектор-анализаторы и ротатор Для ориентации системы координат векторной системы управления необходимо определить текущее положение опорного вектора. Устройства реализующие эти функции обычно называются вектор-анализаторами. Если в системе векторного управления требуется стабилизация потокосцепления, то его текущее значение нужно либо измерить, либо вычислить по другим величинам. Измерение потокосцепления не всегда возможно или желательно, т.к. требует установки в АД соответствующих датчиков и, кроме того, при снижении частоты вращения отношение полезного сигнала к шуму на выходе датчиков снижается настолько, что их использование становится невозможным. В случае потокосцепления ротора его измерение практически невозможно и обычно производится вычисление. Проще всего оно осуществляется, если исходными величинами являются основное потокосцепление и ток статора. Из выражений (1.2.8 б) и (1.2.9) потокосцепление и ток ротора равны Отсюда или после разложения на составляющие в неподвижной системе координат, связанной со статором 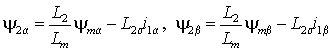 . .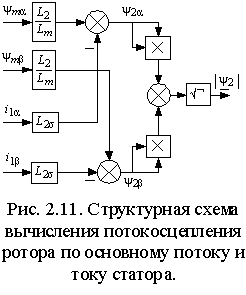 Искомый модуль вектора потокосцепления ротора затем находится по теореме Пифагора . Структурная схема соответствующего блока вычисления приведена на рис. 2.11. Основное потокосцепление 0 можно измерить, установив два датчика Холла так, чтобы один находился на оси обмотки фазы a, а другой на перпендикулярной оси. Тогда выходные сигналы датчиков будут пропорциональны m и m . Составляющие тока статора i1 и i1 получаются из фазных токов преобразованием 3-2 в соответствии с выражениями (1.1.2). 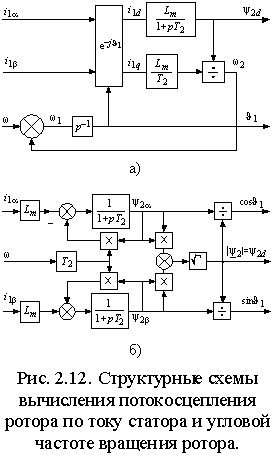 Потокосцепление можно определить и не прибегая к измерению магнитного потока. Достаточно измерить токи статора и угловую частоту вращения ротора. При этом вычисление можно производить во вращающейся или в неподвижной системе координат. Входными величинами в обоих случаях являются токи статора в неподвижной системе координат i1 и i1 и угловая частота вращения ротора . Выходными – модуль вектора потокосцепления ротора | 2|= 2d и, если требуется, текущее значение его аргумента 1. Для вращающейся системы их связь с потокосцеплением ротора определяется выражением (2.2.5), а соответствующая ей структурная схема приведена на рис. 2.12 а). Векторное уравнение ротора в неподвижной системе координат можно получить из выражения (1.4.5), положив (mn) =0. Тогда . Отсюда, подставив , перейдя к изображениям и опуская индексы системы координат, получим . Раскладывая векторы тока статора и потокосцепления ротора на вещественную и мнимую составляющие, получим выражения для проекций потокосцепления в неподвижной системе координат 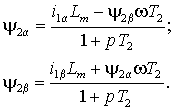 Этим выражениям соответствует структурная схема рис. 2.12 б), в которой затем по проекциям определяются модуль вектора, а также косинус и синус его аргумента – 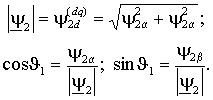 Очевидно, что вычисление потокосцепления без использования датчиков магнитного потока требует построения значительно более сложных устройств, однако в некоторых случаях такое решение оправдано, т.к. установка датчиков и формирование в них выходного сигнала также является достаточно сложной задачей. Кроме того, устройства подобные изображенным на рис. 2.12 могут использоваться в системах асинхронного привода для создания контуров стабилизации магнитного потока ротора, т.е. стабилизации его модуля, что позволяет получить при частотном управлении механические характеристики с одинаковой жесткостью рабочих участков при всех частотах питания, что существенно расширяет диапазон регулирования АД. 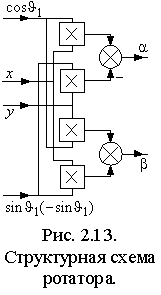 Необходимым элементом системы векторного управления АД является ротатор, осуществляющий преобразование координат векторов в соответствии с выражениями (1.1.5) и (1.1.6). Если сигналы синуса и косинуса угла поворота 1 формируются другим блоком, то ротатор легко реализуется по схеме рис. 2.13. Для вращения в положительном направлении, т.е. для реализации функции , на синусный вход ротатора подается сигнал . Изменение направления вращения осуществляется либо инвертированием сигнала , либо инвертированием сигнала 1. В случае, если входным сигналом ротатора является угол 1, то схема рис. 2.13 должна быть дополнена блоками вычисления функций синуса и косинуса, что очень сложно реализовать практически в аналоговой форме, но легко выполнить в цифровой с помощью соответствующей программы процессора или аппаратно с помощью тригонометрической таблицы, хранящейся в ПЗУ. 2.5. Замкнутые системы векторного управления АД 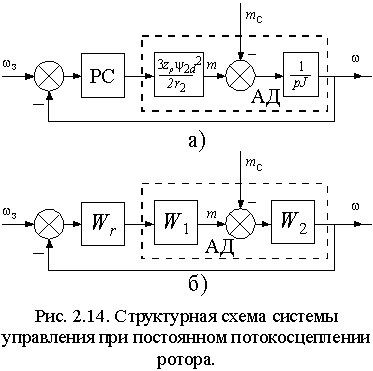 Рассмотренная выше модель АД с векторным управлением, в которой входными сигналами являются потокосцепление и частота ротора, является наиболее простой и распространенной на практике. Она позволяет создавать высокоэффективные системы управляемого асинхронного электропривода аналогичные системам привода постоянного тока. Рассмотрим вопросы построения векторной системы управления скоростью вращения АД. В соответствии с выражением (2.2.7) передаточная функция канала управления частотой ротора или, что тоже самое, электромагнитным моментом при условии стабилизации потокосцепления ротора соответствует интегрирующему звену, что позволяет представить его структурную схему в замкнутой системе управления скоростью вращения с виде рис. 2.14 а) или в общем виде, как показано на рис. 2.14 б), где з– заданная угловая частота вращения ротора, а Wr– передаточная функция регулятора скорости. Передаточные функции по управлению и по возмущению можно представить в общем виде как
Для получения статической системы используют пропорциональный (П) регулятор с передаточной функций
Если требуется получить астатическую систему, используют пропорционально-интегральный (ПИ) регулятор скорости с передаточной функцией
2.5.1. Характеристики системы с П-регулятором скорости 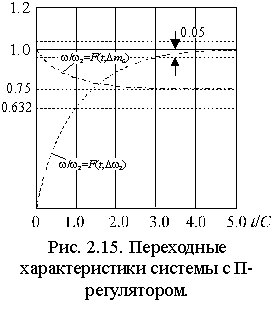 В случае П-регулятора передаточные функции по управлению и возмущению приобретают вид
где ; . Переходные характеристики привода соответствуют экспоненте с постоянной времени C, значение которой обратно пропорционально коэффициенту усиления регулятора K (рис. 2.15). Длительность переходного процесса равна 3 C. Общая передаточная функция системы с П-регулятором имеет вид
и переходит в уравнение регулировочной и механической характеристик при , где . 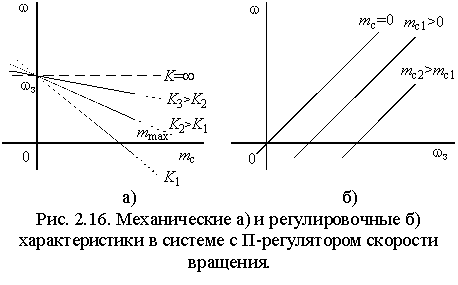 Таким образом, статические характеристики системы векторного управления АД имеют вид, соответствующий характеристикам двигателя постоянного тока (ДПТ) с якорным управлением (рис. 2.16). Их жесткость пропорциональна коэффициенту усиления регулятора K, а статическая ошибка привода – обратно пропорциональна значению этого коэффициента. Формально характеристики могут продолжаться в любую сторону до бесконечности, но, также как в ДПТ, ток машины должен быть ограничен значениями допустимыми по условиям ее эксплуатации, а также по условиям эксплуатации питающего преобразователя. В системе управления ДПТ ток якоря легко ограничить введением после регулятора скорости звена с насыщением. В системе с векторным управлением АД ток статора содержит две составляющие – продольную и поперечную (i1d и i1q), воздействующие соответственно на потокосцепление и электромагнитный момент. Поэтому ограничение управляющих токов на входе усилителя мощности системы недопустимо, т.к. может вызвать уменьшение потокосцепления, и ограничение тока статора можно осуществлять только за счет его поперечной составляющей. Расчет максимально возможного электромагнитного момента можно произвести исходя из заданного значения потокосцепления ротора и максимально допустимого амплитудного значения тока статора , где . Отсюда – 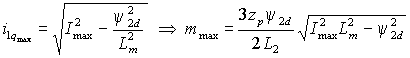 . Для сохранения покосцепления звено с насыщением, рассчитанным на значение нужно вводить в канал поперечной составляющей тока системы управления (рис. 2.3). . Для сохранения покосцепления звено с насыщением, рассчитанным на значение нужно вводить в канал поперечной составляющей тока системы управления (рис. 2.3).В режиме ограничения тока АД с векторным управлением имеет абсолютно мягкую механическую характеристику. 2.5.2. Характеристики системы с ПИ-регулятором скорости Как следует из рисунка 2.14, передаточная характеристика W1 является константой и стандартная настройка ПИ-регулятора невозможна. Попытаемся произвести настройку, исходя из общих принципов коррекции характеристик системы. После подстановки в выражение (2.5.2) передаточной функции регулятора (2.5.4) мы получим передаточную функцию системы по управлению и соответствующую частотную характеристику –
где . Для приближения значения модуля частотной характеристики к единице в возможно более широком диапазоне частот исключим в знаменателе составляющую , т.е. выберем значения коэффициента и постоянной времени регулятора скорости так, чтобы выполнялось условие
Тогда выражения (2.5.8) и (2.5.9) примут вид
где – приведенная угловая частота. С учетом соотношений (2.5.10) можно представить передаточную функцию системы по возмущению в виде
Выражения (2.5.11) и (2.5.13) имеют одинаковые характеристические уравнения, корни которых
соответствуют асимптотически устойчивой системе с колебательным переходным процессом с относительным затуханием и частотой равными друг другу. Причем, т.к. может изменяться от 0 до , то корневые годографы системы всегда лежат в левой полуплоскости. 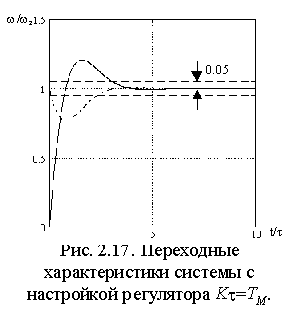 Реакция системы на скачки управляющего и возмущающего воздействий может быть получена из выражений (2.5.11) и (2.5.13) как
где . В этих выражениях время приведено к постоянной времени регулятора скорости . В результате временные параметры переходных функций получаются независимыми от параметров АД (рис. 2.17). Следует заметить, что система не накладывает каких-либо ограничений на значение , т.к. условие настройки всегда можно выполнить соответствующим выбором . Поэтому масштаб времени переходных функций, а, следовательно, и длительность переходного процесса может выбираться произвольно. Анализ выражений (2.5.15) и (2.5.16) показывает:
 Таким образом, предлагаемая настройка ПИ регулятора обладает универсальными параметрами переходного процесса и позволяет получить хорошее качество системы в тех случаях, когда невозможно осуществить стандартную настройку. Пользуясь выражениями (2.5.11) и (2.5.13), можно получить общую передаточную характеристику системы и соответствующие статические характеристики в виде –
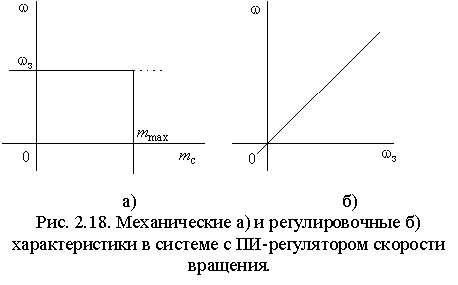
Как и следовало ожидать, полученная система обладает астатизмом первого порядка и абсолютно жесткой механической характеристикой в пределах линейной зоны ограничителя тока (рис. 2.18). Вопросы ограничения тока, рассмотренные для системы с П-регулятором скорости, и связанного с этим ограничения момента в полной мере относятся и к систем с ПИ-регулятором. Список литературы
|

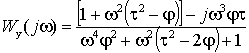 ,
,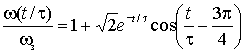
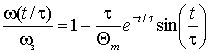 ,
,