24.05.05 Прикладная механика.. Учебное пособие по дисциплине Механика Модуль Прикладная механика
 Скачать 1.89 Mb. Скачать 1.89 Mb.
|
АННОТАЦИЯ ДИСЦИПЛИНЫ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Приставка | Сокращенное обозначение | Множитель |
| Тера | Т | 1012 |
| Гига | Г | 109 |
| Мега | М | 106 |
| Кило | к | 103 |
| Гекто | г | 102 |
| Дека | да | 101 |
| Деци | д | 10-1 |
| Санти | с | 10-2 |
| Милли | м | 10-3 |
| Микро | мк | 10-6 |
| Нано | н | 10-9 |
| Пико | п | 10-12 |
Среди производных единиц с большой буквы пишутся те, которые образованы от фамилий ученых (Гц, Н, Па и т.д.).
Производные единицы связаны с основными, например:
1 Н = 1 кгм/с2; 1 Па=1 Н/м2; 1 Дж=1 Нм; 1 Вт=1 Дж/с.
В некоторых задачах по сопротивлению материалов в исходных данных используются внесистемные единицы, например обороты в минуту или сантиметр в четвертой степени и т.д. Это связано с тем, что на многих работающих сейчас электродвигателях, создающих динамическую нагрузку, обозначено именно количество оборотов в минуту, а в действующих сортаментах на прокат даны геометрические характеристики пока еще в единицах, производных от сантиметра. Переход от этих единиц к системным очевиден. Например:
1см4 = 1(10-2 м)4 = 1∙10-8 м4;
300 об/мин = 5 об/с = 5∙2π Гц.
Основные механические величины в единицах СИ и соотношения между ними и прежними единицами, подлежащими изъятию, приводятся в таблице 2.
Таблица 2
| Наименование величины | Единица | Соотношение единиц | |
| Наименование | Обозначение | ||
| Сила, нагрузка, вес | Ньютон | Н | 1Н ≈ 0,1 кгс 1кН ≈ 0,1 тс |
| Линейная нагрузка | Ньютон на метр | Н/м | 1Н/м ≈ 0,1 кгс/м 1кН/м ≈ 0,1 тс/м |
| Механическое напряжение, модуль упругости | Паскаль | Па | 1Па ≈ 0,1 кгс/м2 1кПа ≈ 0,1 тс/м2 1мПа ≈ 10 кгс/см2 |
| Момент силы, момент пары сил | Ньютон-метр | Нм | 1Нм ≈ 0,1 кгсм 1кНм ≈ 0,1 тсм |
| Работа (энергия) | Джоуль | Дж | 1Дж ≈ 0,1 кгсм |
| Мощность | Ватт (джоуль в секунду) | Вт | 1Вт≈0,1 кгсм/с 1 кВт ≈ 1,36 л.с. |
Основные обозначения
| F, P | - сосредоточенная сила |
| N | - продольная (нормальная) сила |
| q | - интенсивность распределенной нагрузки |
| M | - сосредоточенный момент |
| Qx, Qy | - поперечные силы, направленные вдоль осей x, y |
| Mx, My | - изгибающие моменты в поперечном сечении бруса относительно осей x, y |
| T, Mкр | - крутящий момент в поперечном сечении бруса |
| Mu | - изгибающий момент в поперечном сечении бруса |
| Mэкв | - эквивалентный момент |
| b | - ширина |
| t | - толщина |
| e | - эксцентриситет силы |
| l | – длина, пролет |
| x | - продольная ось стержня |
| y, z | - главные центральные оси инерции поперечного сечения стержня. |
| σ | - нормальное напряжение (общее обозначение) |
| σx, σy | – нормальные напряжения на площадках с нормалями параллельными осям x и y |
| τ, τα, τxy | - касательное напряжение (общее обозначение) |
| σэкв | - эквивалентное напряжение |
| σсм | - нормальное напряжение при смятии |
| σy | - предел текучести |
| σut | – предел прочности при растяжении |
| σuc | – предел прочности при сжатии |
| σmax, σmin, σm, σa | - нормальные напряжения цикла: максимальное, минимальное, среднее, амплитуда |
| τa, τm | - касательные напряжения цикла: амплитуда и среднее |
| σm | - средние напряжения |
| σв | - временное сопротивление (предел прочности) |
| σ-1, τ-1 | - пределы выносливости при симметричном цикле изгиба и кручения |
| σ0, τ0 | - пределы выносливости при отнулевом цикле изгиба и кручения |
| R | - расчетное сопротивление |
| [σ], [τ] | - допускаемые нормальное и касательное напряжения |
| n | - коэффициент запаса прочности |
| [n] | - допускаемый (требуемый) коэффициент запаса прочности |
| ∆l | - абсолютное удлинение (абсолютная линейная деформация) |
| Ε | - относительное удлинение (относительная линейная деформация) |
| εt | - поперечная деформация |
| γ | - угол сдвига (относительная угловая деформация) |
| E | - модуль продольной упругости |
| G | - модуль упругости при сдвиге (модуль сдвига) |
| Μ | - коэффициент Пуассона |
| W | - работа внешних сил |
| U | - потенциальная энергия деформации |
| φ | - угол поворота поперечного сечения бруса при кручении |
| f | - прогиб балки |
| θ | - угол поворота поперечного сечения балки при изгибе |
| A | - площадь поперечного сечения бруса брутто |
| Sx, Sy | - статические моменты сечения относительно осей x, y |
| Ix, Iy | - осевые моменты инерции сечения относительно осей x, y |
| Ip | - полярный момент инерции сечения |
| Ixy | - центробежный момент инерции сечения |
| ix, iy, iz | - радиусы инерции сечения относительно соответствующих осей |
| imin | - наименьший радиус инерции сечения |
| Wx, Wy, Wz | – моменты сопротивления сечения относительно осей x–x, y–y и z–z соответственно |
| Wp | - полярный момент сопротивления сечения |
| Kσ, Kτ | - эффективные коэффициенты концентрации напряжений |
| KF | - коэффициент влияния шероховатости поверхности на предел выносливости |
| KV | - коэффициент влияния упрочнения поверхности на предел выносливости |
| Kd | - коэффициент влияния абсолютных размеров поперечного сечения на предел выносливости |
| Pкр | - критическая сила |
| σcr, σкр | - критическое напряжение |
| λ | - гибкость стержня |
1.ЗАДАЧИ И МЕТОДЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Сопротивление материалов это наука об инженерных методах расчета на прочность, жесткость и устойчивость элементов сооружений и деталей машин.
Элементы сооружений отличаются друг от друга формами, размерами, материалом, функциональным назначением, рядом специальных требований. При этом следует отметить, что все без исключения элементы как искусственного, так и естественного происхождения обладают такими свойствами, как прочность и жесткость, то есть способностью, не разрушаясь воспринимать различные нагрузки и сопротивляться изменению своих первоначальных форм и размеров, без чего не может нормально функционировать сооружение. Цель расчетов в сопротивлении материалов – создание прочных, устойчивых, обладающих достаточной жесткостью, долговечностью и вместе с тем экономичных элементов сооружений
Прочностные и жесткостные качества элементов сооружений зависят от многих факторов: материала, размеров, характера возникающих деформаций и др. Металлические конструкции обладают большей прочностью и жесткостью, чем аналогичные деревянные конструкции. Стержень из одного и того же материала, имеющий большие поперечные размеры, более прочный и жесткий, при этом его легче разрушить, изгибая, чем растягивая. Тонкий стержень при его сжатии разрушается в результате выпучивания в поперечном направлении, в то же время это явление отсутствует при продольном растяжении и для разрушения стержня требуется значительно большая нагрузка.
Подведя итог можно утверждать, что всякое реальное тело под воздействием сил меняет свою форму и размеры, т. е. деформируется. Деформации обуславливают появление внутри элемента сил сопротивления. Если внешние силы больше сил сопротивления, происходит разрушение элемента сооружения.
При возрастании нагрузки выше определенных значений в теле наряду с упругими будут возникать деформации не исчезающие после снятия нагрузки. Такие деформации называются остаточными. Возникновение остаточных деформаций, наравне с разрушением связано с нарушением нормальной работы конструкции и, как правило, недопустимо.
Способность конструкции воспринимать заданную нагрузку, не разрушаясь и без остаточных деформаций, называют прочностью.
Все элементы сооружения, из каких бы материалов они ни были изготовлены, под нагрузкой деформируются. Однако значительные деформации могут мешать нормальной эксплуатации сооружения.
Способность сооружений и ее частей под нагрузкой сохранять свои размеры и форму в установленных нормами пределах называется жесткостью.
Способность конструкции, и ее частей, сохранять под нагрузкой первоначальную форму упругого равновесия называется устойчивостью.
Методами сопротивления материалов выполняются расчеты, на основании которых определяются необходимые размеры деталей машин и конструкций инженерных сооружений. Любая конструкция должна обладать надежностью при эксплуатации и быть экономичной.
Надежность– свойство конструкции выполнять заданные функции, сохраняя свои эксплуатационные показатели в определенных нормативных пределах в течение требуемого промежутка времени.
Ресурс – допустимый срок службы изделия. Указывается в виде общего времени наработки или числа циклов нагружения конструкции.
Отказ– нарушение работоспособности конструкции.
Опираясь на вышесказанное, можно дать определение прочностной надежности.
Прочностной надежностью называется отсутствие отказов, связанных с разрушением или недопустимыми деформациями элементов конструкции.
Надежность конструкции обеспечивается, если она сохраняет прочность, жесткость и устойчивость при гарантированной долговечности. Ее экономичность в значительной мере определяется расходом материала, применением менее дефицитных конструкционных материалов, возможностью изготовления деталей по наиболее прогрессивным технологиям. Надежность и экономичность - противоречивые требования.
В сопротивлении материалов широко применяются методы теоретической механики и математического анализа, используются данные из разделов физики, изучающих свойства различных материалов, материаловедения и других наук. К тому же сопротивление материалов является наукой экспериментально-теоретической, так как она широко использует опытные данные и теоретические исследования.
В отличие от теоретической механики сопротивление материалов рассматривает задачи, в которых наиболее существенными являются свойства твердых деформируемых тел, а законами движения тела как жесткого целого здесь пренебрегают. В теоретической механике рассматривают равновесие абсолютно твердого (недеформированного) тела, при составлении уравнений равновесия допустимы замена системы сил статически эквивалентной системой, перенос сил вдоль линии их действия, замена ряда сил их равнодействующей. При решении задач сопротивления материалов, подобные замены или перенос сил недопустимы.
Методы сопротивления материалов базируются на упрощенных гипотезах, которые, с одной стороны, позволяют решать широкий круг инженерных задач, а с другой, получать приемлемые по точности результаты расчетов.
При этом главной задачей курса является формирование знаний для применения математического аппарата при решении прикладных задач, осмысления полученных численных результатов и поиска выбора наиболее оптимальных конструктивных решений. Конечная цель науки сопротивления материалов – определение размеров элементов сооружений, обеспечивающих его работоспособность при минимальном расходе материалов.
Сопротивление материалов является основой для изучения курса «Детали машин».
Зарождение науки о сопротивлении материалов относится к XVII в. и связано с работами знаменитого ученого того времени Галилео Галилея. Значительный вклад в ее развитие был сделан выдающимися учеными: Гуком, Бернулли, Сен-Венаном, Коши, Ламе, Эйлером и др. В России в конце XIX-начале XX века важные исследования в области сопротивления материалов провели русские ученые Д.И.Журавский,
Ф.С.Ясинский, И.Г.Бубнов, С.П.Тимошенко и др.
1.1.Реальный объект и расчетная схема.
В сопротивлении материалов, как и во всякой отрасли естествознания, исследование вопроса о прочности или жесткости реального объекта начинается с выбора расчетной схемы. Расчетная схема конструкции это его упрощенная схема, освобожденная от несущественных в данной задаче особенностей. К числу существенных факторов расчетной схемы относят: геометрию объекта, его форму и размеры; физические характеристики материала; нагрузки, прикладываемые к объекту. Например, при расчете на прочность троса, поднимающего груз, можно не учитывать форму груза, сопротивление воздуха, изменение давления и температуры воздуха с высотой, силу тяжести троса и многие другие факторы, учет которых усложняет расчет троса, но практически не влияет на конечный результат. Трос, свитый из большого числа тонких проволочек, в данном примере можно рассматривать как однородный стержень круглого поперечного сечения, нагруженный растягивающей силой, сосредоточенной в месте крепления груза.
Такого рода упрощения задачи совершенно необходимы, так как решение с полным учетом всех свойств реального объекта является принципиально невозможным в силу их очевидной неисчерпаемости.
Основным упрощающим приемом в сопротивлении материалов является приведение геометрической формы тела к схемам бруса (стержня), оболочки или пластины. Как известно, любое тело в пространстве характеризуется тремя измерениями.
Под стержнями подразумеваются тела довольно разнообразной и вместе с тем специфической формы. Представим себе некоторую линию, вдоль которой движется плоская фигура так, что её центр тяжести находится на этой линии, а плоскость фигуры нормальна к ней (рис. 1.1). Если размеры фигуры b, h существенно меньше длины линии l, то описанное указанным образом тело называется стержнем (или брусом);
соответственно отмеченная плоская фигура называется поперечным сечением стержня, а отмеченная линия – осью стержня.

Рис. 1.1 Прямой брус (стержень) постоянного сечения
Если поперечное сечение при движении вдоль оси не изменяется, то тогда имеет место стержень постоянного сечения; в противном случае – стержень переменного сечения. Если ось стержня – прямая линия, то это прямой стержень. Если ось стержня – кривая линия, то его называют кривымстержнем. Используются также и другие названия, в частности, брус, работающий на растяжение, называют стержнем (рис.1.2, а), на изгиб, обычно называют балкой, а стержень, передающий вращательное движение, – валом. Стержневые элементы, воспринимающие вертикальные сжимающие силы, называют стойками, а наклонные элементы - раскосами. Конструкцию, состоящую из соединенных изгибаемых стержней, называют рамой. Если же благодаря шарнирному соединению стержней все они работают только на растяжение или сжатие (от нагрузки, приложенной в узлах), то конструкцию называют фермой.
Второй основной геометрической формой, рассматриваемой в сопротивлении материалов, является оболочка, под которой подразумевается тело, у которого одно из измерений (толщина) намного меньше, чем два других (рис.1.2, в). К оболочкам относятся различного рода резервуары, котлы, купола зданий, корпуса подводных лодок, обшивка фюзеляжа самолета и т.п.
Срединная поверхность – это геометрическое место точек, равноудаленных от внешней и внутренней поверхностей оболочки.
Оболочка, срединная поверхность которой представляет собой плоскость, называется пластиной(рис.1.2, б). Примером могут служить крыши и днища резервуаров, перекрытия зданий, различные диски и т.п.
Элемент конструкции, размеры которого во всех направлениях мало отличаются друг от друга, называется массивом. К ним относятся фундаменты сооружений, подпорные стенки и т.п.
Методы расчета пластин, оболочек и массивных тел при больших деформациях рассматриваются в курсе «Прикладная теория упругости». Способы расчета стержневых систем изучаются в курсе «Строительная механика».
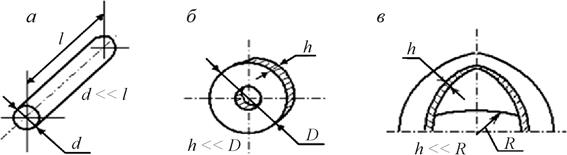
Рис. 1.2. Основные модели формы в моделях прочностной надежности:
а – стержень; б – пластина; в – оболочка
В заключение отметим, что если для одного объекта может быть предложено несколько расчетных схем, то, с другой стороны, одной расчетной схеме может быть поставлено в соответствие много различных реальных объектов.
Последнее обстоятельство является весьма важным, так как исследуя некоторую схему, можно получить решение целого конкретных задач, сводящихся к данной схеме.
1.2.Связи и опорные устройства.
Для соединения отдельных частей конструкции между собой и передачи внешней нагрузки на основание на нее накладываются связи, ограничивающие перемещения тех точек сооружения, к которым они приложены. Связи могут ограничивать либо повороты точек сооружения, либо их линейные смещения, либо и то и другое.
Основным видом связей в расчетной схеме является шарнирная связь.
Простой шарнир (рис. 1.3) накладывает две связи.
Рис. 1.3.
В расчетную схему входит основание, т.е. тело, на котоpое опирается cистема в целом, считающееся неподвижной.
Неподвижность расчетной схемы относительно основания обеспечивается опорными связями (опорами).
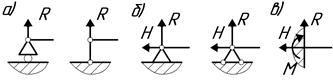
Рис. 1.4 Опорные связи (опоры).
Все опорные связи условно делятся на три основных типа:
- Подвижная шарнирнаяопора (рис.1.4, а). Такая опора не препятствует вращению конца бруса и его перемещению вдоль плоскости качения. В ней может возникать только одна реакция, которая перпендикулярна плоскости качения и проходит через ось катка (R).
- Неподвижная шарнирная опора (рис.1.4, б). Такая опора допускает вращение конца бруса, но устраняет поступательное движение ее в любом направлении. Возникающую в ней реакцию можно разложить на две составляющие, одна из которых направлена вдоль оси бруса (Н), другая - перпендикулярно к оси бруса (R).
- Жесткая заделка или защемление (рис.1.4, в). Такое закрепление не допускает ни линейных, ни угловых перемещений опорного сечения. В этой опоре в общем случае может возникать реакция, которую обычно раскладывают на две составляющие (H и R) и момент защемления (М).
При рассмотрении реального объекта в число внешних сил включаются не только заданные нагрузки, но и реакции связей (опор), дополняющие систему сил до равновесного состояния.
Внешние и внутренние силы. Метод сечений
Силы являются мерилом механического взаимодействия тел. Если конструкция рассматривается изолированно от окружающих тел, то действие последних на нее заменяется силами, которые называютсявнешними. Внешние силы, действующие на тело, можно разделить на активные(независимые) и реактивные. Реактивные усилия возникают в связях, наложенных на тело, и определяются действующими на тело активными усилиями.
По способу приложения внешние силы делятся на
объемные и поверхностные.
Объемные силы распределены по всему объему рассматриваемого тела и приложены к каждой его частице. В частности, к объемным силам относятся собственный
вес сооружения, магнитное притяжение, сила тяжести или силы инерции. Единицей
измерения объемных сил является сила, отнесенная к единице объема кН/м3.
Поверхностные силы приложены к участкам поверхности и являются результатом непосредственного контактного взаимодействия рассматриваемого объекта с окружающими телами (давление ветра, воды на стенку).
В зависимости от соотношения площади приложения нагрузки и общей площади поверхности рассматриваемого тела, поверхностные нагрузки подразделяются на
сосредоточенныеи распределенные.
Если давление q1 (Н/м2) передается на элемент конструкции через площадку, размеры которой очень малы по сравнению с размерами всего элемента (a≪l), то его на основании принципа Сен-Венана можно привести к сосредоточенной силе F (рис. 1/5). Например, воздействие колонн на фундаментную плиту достаточно больших размеров можно рассматривать как действие на нее сосредоточенных усилий.
Сосредоточенная сила F измеряется в ньютонах (Н), килоньютонах (кН). Подобным образом вводятся понятия сосредоточенных изгибающих и крутящих моментов.
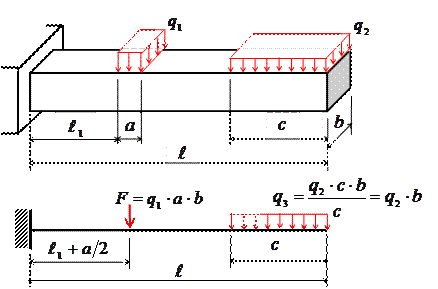
Рис. 1/5
Если давление q2 (Н/м2) передается на элемент конструкции через площадку, размеры которой сравнимы с размерами всего элемента (c<l), то его представляют в виде распределенной или погонной нагрузкиq3 с размерностью кН/м или кН/м2 (рис. 5). Примером может служить собственный вес балки, действие снеговой или ветровой нагрузки на сооружение, давление жидкости в резервуаре. Распределенная нагрузка может действовать и по линии как, например, при соприкасании двух цилиндров при параллельном расположении их осей.
На расчетной схеме вместо бруса изображается его ось. Нагрузки, распределенные по линии и сосредоточенные в точках, реально не существуют. Их можно получить лишь в результате схематизации реальных нагрузок, распределенных по объему (объемных сил) и по поверхности.
По характеру изменения силы во времени различают нагрузки статические и динамические. Статические нагрузки (постоянные) - такие, которые изменяют свою величину или точку приложения (направление) с очень небольшой скоростью, так что возникающими при этом ускорениями (силами инерции) можно пренебречь. Динамическиенагрузки - изменяются во времени с большой скоростью, при этом силы инерции должны быть учтены, так как оказывают существенное влияние на конструкцию. Динамические нагрузки подразделяются на внезапно приложенные, повторно-переменные и ударные. Примером внезапно приложенной нагрузки может служить действие веса железнодорожного состава, проходящего через мост; повторно-переменной – нагрузка на шатун в двигателе внутреннего сгорания; ударной – действие силы удара молота на его фундамент или гидравлический удар в гидросистеме. Ударные нагрузки возникают также в случае плохой пригонки или износа сопряженных деталей, когда зазоры превышают величину, допустимую по конструктивным и технологическим условиям. Например, при износе зубьев шестерен или деталей шариковых подшипников в машине возникают характерные стуки, свидетельствующие о возникновении ударных нагрузок, быстро приводящих к выходу конструкции из строя.
Временная нагрузка может сохранять более или менее постоянную величину в течение всего периода ее действия, а может непрерывно изменяться по некоторому закону; в последнем случае она называется переменнойнагрузкой.
Если переменная нагрузка изменяется по циклическому (повторяющемуся) закону, то она называется циклической.
В машиностроении расчетные нагрузки определяются в зависимости от конкретных условий работы машины: по номинальным значениям мощности, угловой скорости отдельных ее деталей, силы тяжести, сил инерции и т. п.
При систематическом чередовании нагружения и разгрузки накопление дефектов структуры ведет к возникновению микроскопических трещин, слияние которых приводит к усталостному разрушению.
По отношению к выбранному материальному телу (элементу конструкции) все действующие силы подразделяются на внешние и внутренние силы. Под внешними силами (нагрузками) понимаются силы взаимодействия данного материального тела со всеми другими окружающими его телами.
Взаимодействие между частями рассматриваемого тела характеризуется
внутреннимисилами,которые возникают внутри тела под действием внешних нагрузок и определяются силами межмолекулярного воздействия. Эти силы сопротивляются стремлению внешних сил разрушить элемент конструкции, изменить его форму, отделить одну часть от другой. Вообще внутренние силы возникают между всеми смежными частицами тела при нагружении.
Для выявления внутренних сил и последующего их определения применяют метод сечений,суть которого заключается в следующем. Пусть к элементу сооружения, имеющего форму бруса, приложена система внешних сил, удовлетворяющая условиям равновесия. Под действием этой нагрузки в элементе возникают внутренние силы. В произвольном месте мысленно рассечем брус поперечным сечением на две части (рис. 1.6, а).
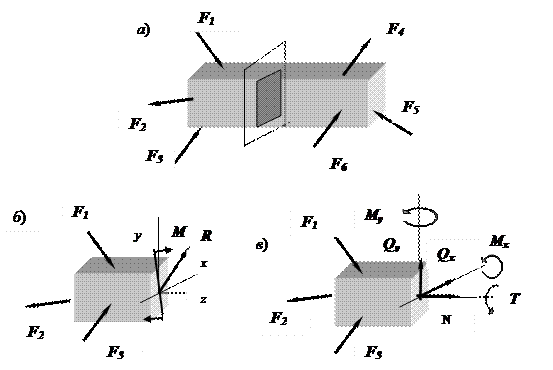
Рис.1.6. Определение внутренних сил методом сечений: а) – элемент до рассечения поперечным сечением;
б) – приведение системы внутренних сил к центру тяжести сечения; в) – разложение главного вектора и главного момента по осям координат
Так как связи между частями устранены, то необходимо действие правой части на левую, и левой на правую заменить системой сил в этом сечении. Эти силы определяют взаимодействие между частицами тела, расположенными по разные стороны от мысленно проведенного сечения, и поэтому являются внутренними для тела в целом. Согласно закону действия и противодействия система сил, возникающих на поверхности сечения в левой отсеченной части,равна, но обратна по знаку системе сил на поверхности сечения в правой отсеченной части. Согласно допущению о сплошности материала следует считать, что внутренние силы распределены по сечению непрерывно по некоторому не известному нам закону.
Внутренние усилия должны быть так распределены по сечению, чтобы деформированные поверхности сечения при совмещении правой и левой частей тела в точности совпадали. Это требование в механике твердого деформируемого тела носит название условия неразрывности деформаций.
Рассмотрим отдельно какую-либо из отсеченных частей бруса, например левую. Внутренние силы, возникающие в сечении целого бруса по отношению к рассматриваемой отсеченной части бруса, являются внешними и дополняют систему заданных внешних сил до равновесной. Приведем систему внутренних сил к центру тяжести сечения (рис. 1.6, б). В результате получим главный вектор R и главный момент M.
Выберем систему координат так, чтобы ось z совпала с нормалью к сечению (располагалась вдоль оси элемента), а оси у и x лежали в плоскости нормального сечения. Разложив главный вектор и главный момент по осям координат, получим составляющие: три силы и три момента. Эти составляющие называют внутренними силовыми факторами в сечении бруса, каждая из которых имеет свое наименование: N - нормальная сила; Qy и Qz - поперечные силы; Т - крутящий момент; Mzи Му - изгибающие моменты относительно осей x и y (рис. 1.6, в).
При известной нагрузке все шесть внутренних силовых факторов могут быть определены из уравнений равновесия составленных для рассматриваемой части бруса. Заметим, что в каждое уравнение войдут проекции на соответствующую ось (или моменты относительно оси) всех внешних сил, приложенных к рассматриваемой части, и только один из внутренних силовых факторов.
ΣZ = ΣFzотс + N = 0; Σmz = ΣMzотс + T = 0;
ΣY = ΣFyотс + Qy = 0; Σmy = ΣMyотс + My = 0;
ΣX = ΣFxотс + Qx = 0; Σmx = ΣMxотс + Mx = 0.
Уравнения равновесия позволяют сформулировать правило определения каждого из внутренних силовых факторов:
Продольная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на ось z, всех внешних сил, действующих на одну из отсеченных (левую или правую) частей бруса.
N = ΣFzотс.
То же для определения поперечных сил Qy и Qx,,только проектировать внешние силы необходимо на оси y и x.
Qy = ΣFyотс,
Qx = ΣFxотс.
Изгибающие моменты Mx и My и крутящий момент T, численно равны алгебраической сумме моментов всех сил по одну сторону от сечения, относительно соответствующих осей x, y и z.
T = ΣMzотс,
Mx = ΣMxотс,
My = ΣMyотс.
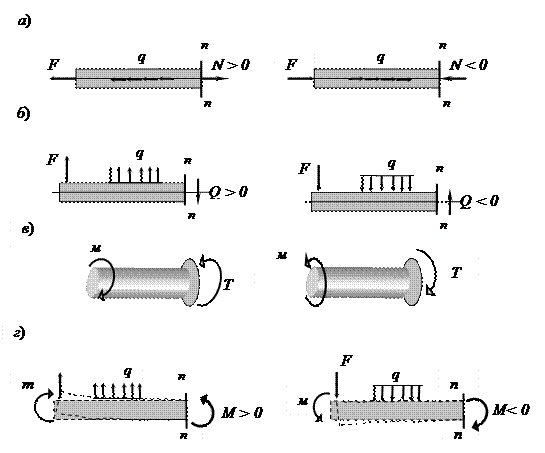
Для установления знака внутреннего силового фактора будем придерживаться следующих правил:
Условимся продольную силу считать положительной, если она вызывает растяжение, т.е. направлена от сечения и отрицательной, если она вызывает сжатие, т. е. направлена к сечению.
При решении задач знак N удобнее устанавливать в зависимости от направления внешних сил. Если внешняя сила, направлена в противоположную от сечения сторону, то она вызывает в нем положительную продольную силу (растяжение), и наоборот, если внешняя сила, направлена к сечению, то она вызывает в нем отрицательную продольную силу (сжатие) (рис. 1.7, а).
Поперечную силу Q будем считать положительной, если она направлена так, что стремиться повернуть отсеченную часть бруса по ходу часовой стрелки (рис. 1.7, б), и отрицательной, если - против хода часовой стрелки.
Согласно этому правилу внешняя сила, стремящаяся повернуть рассматриваемую часть бруса относительно сечения по ходу часовой стрелки, вызывает в сечении положительную поперечную силу
Крутящий момент Т будем считать положительным, если при взгляде со стороны внешней нормали на рассматриваемое сечение он направлен по ходу часовой стрелки или внешний скручивающий момент направлен против хода часовой стрелки (рис.1.7, в).
Изгибающий момент Mx считается положительным, если он вызывает растяжение нижних волокон рассматриваемой части бруса. В противном случае изгибающий момент считается отрицательным (рис. 1.7, г).