24.05.05 Прикладная механика.. Учебное пособие по дисциплине Механика Модуль Прикладная механика

• Название: Учебное пособие по дисциплине Механика Модуль Прикладная механика
• Дата: 17.04.2023
• Размер: 1.89 Mb.
• Имя файла: 24.05.05 Прикладная механика..docx
• Тип: Учебное пособие; #1068488
• страница: 8 из 18

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

- Для чего необходимо знать механические характеристики материала?

- Какие виды испытаний материалов применяются на практике?

- Какая испытательная техника используется для испытания материалов?

- Какие характерные точки имеет диаграмма растяжения стали?

- Что называется пределом пропорциональности, пределом упругости, пределом текучести и пределом прочности?

- Какое явление называют текучестью?

- Что такое «шейка», в какой точке диаграммы растяжения она образуется?

- В чем различия между упругими и пластичными деформациями?

- Перечислите характеристики прочности?

- Перечислите характеристики пластичности?

- Назовите все характеристики прочности материала. Сколько их?

- Какие материалы считаются хрупкими?

- Что называется модулем продольной упругости Е? Как сказывается величина Е на деформации бруса?

- Как формулируется закон Гука?

- Что называют коэффициентом Пуассона и в каких пределах он принимает значения для различных материалов?

- Какое явление называют “наклёпом” (нагартовкой)?

- Что называют упругостью, пластичностью, ползучестью?

- Чем отличаются диаграммы растяжения и сжатия для пластичных материалов?

- Чем отличаются диаграммы растяжения и сжатия для хрупких материалов?

- Какие материалы называют анизотропными?

- Какая из механических характеристик выбирается в качестве предельного напряжения для пластичных и хрупких материалов?

- В чем различие между предельным и допускаемым напряжениями?

- Что называется относительной продольной и относительной поперечной деформацией? Для чего они определяются?

- Можно ли определить модуль упругости Е по диаграмме растяжения?

- Что понимается под наклепом материала?

- Что выражает собой площадь диаграммы растяжения?

- Что представляет собой коэффициент запаса прочности, с какой целью и как его назначают? 

3. Осевое растяжение – сжатие.

3.1. Продольные силы в поперечных сечениях
Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.

Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений.

Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис. 3.1.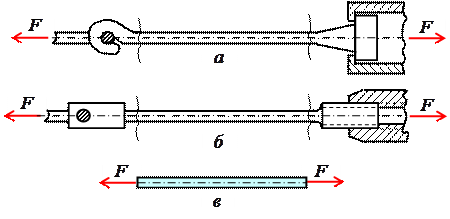

 



Рис. 3.1

 

Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис. 3.1, а, б) оказывается единой (рис. 3.1, в) согласно принципу Сен – Венана.

Если воспользоваться методом сечений (рис. 3.2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы N_z, равные силе F (рис. 3.2, б).

Сжатие отличается от растяжения, формально говоря, только знаком силы N_z. При растяжении нормальная сила N_z  направлена от сечения (рис. 3.2, б), а при сжатии – к сечению.


Рис. 3.2

 

Растягивающие продольные силы принято считать положительными (рис. 3.3, а), а сжимающие – отрицательными(рис. 3.3, б).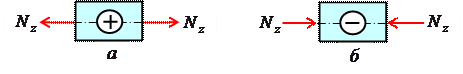
 



Рис. 3.3

 

При расчете стержней, испытывающий деформацию растяжения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от N_z), возникающих в стержне, и нахождение линейных перемещений в зависимости от внешней нагрузки.

Продольные силы (N_z), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений.

График, показывающий изменение продольных сил по длине оси стержня, называется эпюрой продольных сил (эп.N_z). Он дает наглядное представление о законе изменения продольной силы.

 Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.

Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти N_max при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.

Перед построением эпюр необходимо освободить брус, в котором будем строить эпюры от опорных связей (выделить объект равновесия) и приложить к нему все действующие внешние силы (активные и реактивные). Затем необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный. Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня.

Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса.

Рассмотрим стержень постоянного поперечного сечения, жестко защемленный правым концевым сечением и нагруженный заданной внешней сосредоточенной нагрузкой F и распределенной q (рис. 3.4, а).

Прежде всего определим опорную реакцию R₁, задавшись ее направлением вдоль оси z.

ΣF_z=0,   -R₁ - 22 + 24∙0,6 = 0,    R₁= -7,6 кН.

Знак минус говорит о том, что действительное направление опорной реакции R₁ противоположно показанному на рис. 3.4, а. Исправляем его и в дальнейших расчетах знак минус у опорной реакции R₁ не учитываем (рис. 3.4, в, г).

Под участкомбудем понимать часть стержня, на которой N_z  представляется некоторым аналитическим выражением. На другом участке N_z  будет определяться другой функцией.

Границами участка являются начало и конец стержня, сечения, где приложены сосредоточенные нагрузки, начинается и заканчивается распределенная нагрузка.

В нашем случае стержень разбивается на два участка. В пределах первого участка мысленно рассечем стержень на две части нормальным сечением (рис. 3.4, б, в).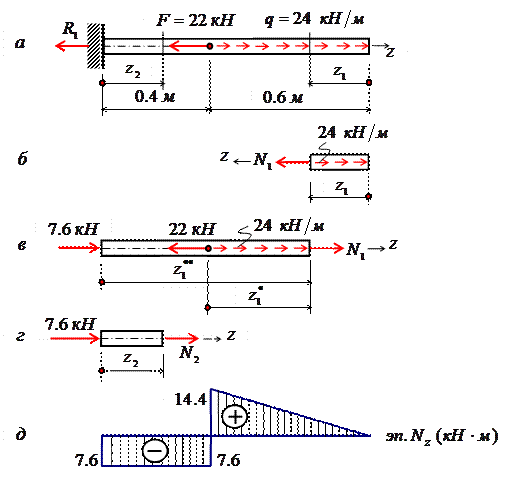



Рис. 3.4

 

Направления продольных сил (рис. 3.4, б – г) приняты в предположении, что они являются растягивающими (т. е. положительными). Если в результате расчета значение N_i получится со знаком «минус», то это будет означать, что в действительности стержень в этом сечении сжат.

Поскольку обе части стержня являются равноправными, то N₁ на первом участке в сечении, определяемом координатой z₁, можно определить рассматривая равновесие его правой (рис. 3.4, б) либо левой (рис. 2.4, в) частей.

В нашем случае для определения N₁ предпочтительнее рассмотреть равновесие правой части – к ней приложено меньше сил (рис. 3.4, б). Начало координат совмещаем с правым концевым сечением первого участка. Ось z направляем налево. Пределы изменения положения сечения вдоль продольной оси  0≤z₁≤0,6 м. Спроектируем все силы, действующие на правую часть, на продольную ось.

ΣF_z=0,   N₁ - 24∙z₁ = 0,    N₁ =24∙z₁,   N₁(0)= 0,    N₁(0,6)= 14,4 кН.

Поскольку функция N₁ =24∙z₁ получилась линейная, то для построении графика ее изменения вдоль продольной оси (эп.N_z) достаточно вычислить значения продольной силы на границах первого участка, отложить их перпендикулярно продольной оси вверх (стержень растянут) и провести через них прямую линию (рис. 3.4, д).

Таким образом, в пределах первого участка стержень растянут и нормальная сила изменяется по линейному закону.

Этот же результат можно получить, рассматривая равновесие левой части стержня.

Здесь при выборе системы координат рассмотрим два варианта. При первом варианте начало координат совмещаем с левым концевым сечением второго участка. Ось z направляем направо. Пределы изменения положения сечения вдоль продольной оси 0,4 м≤ ≤1,0 м. Спроектируем все силы, действующие на левую часть, на продольную ось.

ΣF_z=0,   N₁ +7,6 – 22 + 24∙(  - 0,4)= 0,    N₁ =24- 24∙ ,   N₁(0,4)= 14,4 кН,    N₁(1,0)= 0.

Во втором варианте введем скользящую систему координатных осей. Начало координат совмещаем с левым концевым сечением первого участка. Ось z направляем направо. Пределы изменения положения сечения вдоль продольной оси 0≤ ≤0,6 м. Имеем

ΣF_z=0,   N₁ +7,6 – 22 + 24∙  = 0,    N₁ =14,4- 24∙ ,   N₁(0)= 14,4 кН,    N₁(0,6)= 0.

Заметим, что при выборе скользящей системы координат, функция N₁=f(z, q) меняется от нуля, что делает последующие расчеты менее трудоемкими.

Сравнивая все три варианта определения N₁, приходим к выводу, что когда мы оставляем ту часть стержня, к которой приложено меньше внешних нагрузок, то расчеты оказываются более простыми.

При некотором навыке можно сразу составить выражение для N₁, не изображая отдельные части бруса, на которые он расчленяется поперечными сечениями (рис. 3.4, б, в). Например,

при  0≤z₁≤0,6 м,  N₁ =24∙z₁;  

при  0,4 м≤ ≤1,0 м,  N₁ =7,6 + 22 - 24∙( -0,4);

при 0≤ ≤0,6 м,  N₁ = -7,6 + 22 - 24∙ .

Таким образом, на основании метода сечений продольная сила в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на его продольную ось.

Причем проекция внешней силы берется со знаком плюс, если сила растягивает часть стержня от точки ее приложения до рассматриваемого сечения и, наоборот, со знаком минус – если сжимает.

Осталось определить значение продольной силы N₂ в произвольном сечении, определяемом координатой z₂, на втором участке (рис. 3.4, г). Так как продольная сила N₂ численно равна алгебраической сумме внешних сил, приложенных к стержню слева от сечения (рассматриваем равновесие левой части стержня), то N₂= -7,6 кН (реакция R₁=7,6 кН сжимает часть стержня длиной z₂). Здесь принимаем скользящую систему координат, с началом в левом концевом сечении второго участка. Ось z направляем направо.

Эпюра N_z на втором участке представлена на рис 3.4, д в виде прямоугольника со знаком минус, поскольку N₂= -7,6 кН =const. Таким образом, в пределах второго участка стержень претерпевает сжатие постоянной нормальной силой.

Каждая ордината эп.N_z  (рис. 3.4, д) в принятом масштабе равна величине продольной силы, действующего в том поперечном сечении стержня, которому соответствует эта ордината.

Видно, что на участке между точками приложения сосредоточенных сил R₁ и  F  продольная сила имеет постоянное значение, а на участке, где приложена распределенная внешняя нагрузка, меняется по линейному закону (рис. 3.4, д).

Характерно, что скачки на эп.N_z  обусловлены наличием в соответствующих сечениях сосредоточенных сил R₁ и F.

3.2. Напряжение в поперечных сечениях стержня
Нормальная сила N приложена в центре тяжести сечения, яв­ляется равнодействующей внутренних сил в сечении и, в соответст­вии с этим, определяется следующим образом:



Но из этой формулы нельзя найти закон распределения нор­мальных   напряжений в поперечных сечениях стержня. Для этого обратимся к анализу характера его деформирования.

Если на боковую поверхность этого стержня нанести прямо­угольную сетку (рис. 3.2, б), то после нагружения поперечные ли­нии аа, bb и т.д. переместятся параллельно самим себе, откуда следует, что все поверхностные продольные волокна удлинятся одинаково. Если предположить также, что и внутренние волокна работают таким же образом, то можно сделать вывод о том, что по­перечные сечения в центрально растянутом стержне смещаются параллельно начальным положениям, что соответствуетгипотезе плоских сечений (гипотезе Бернулли).

Значит, все продольные волокна стержня находятся в одина­ковых условиях, а следовательно, нормальные напряжения во всех точках поперечного сечения должны быть также одинаковы и рав­ны



где A  площадь поперечного сечения стержня.

В сечениях, близких к месту приложения внешних сил, гипотеза Бернулли нарушается: сечения искривляются, и напряжения в них распределяются неравномерно. По мере удаления от сечений, в которых приложены силы, напряжения выравниваются, и в сечениях, удаленных от места приложения сил на расстояние, равное наибольшему из размеров поперечного сечения, напряжения можно считать распределенными по сечению равномерно. Это положение, называемое принципом Сен-Венана, позволяет при определении напряжений в сечениях, достаточно удаленных от мест приложения внешних сил, не учитывать способ их приложения, заменять систему внешних сил статически эквивалентной системой. Например, экспериментально установлено, что во всех трех случаях нагружения стержня (рис. 3.7, а) значения напряжений в сечениях, удаленных от крайних сечений на расстояние не менее высоты сечения h, одинаковы:   (рис. 3.7, б), а в сечениях, близких к местам приложения внешних сил, распределения напряжений по сечению существенно различны (рис. 3.7, в).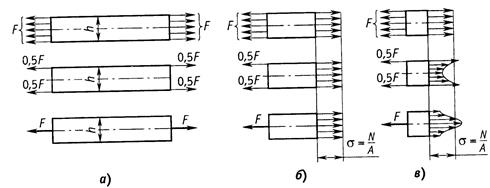          



Рис. 3.7

 

Высказанное предположение о равномерном распределении нормальных напряжений в поперечном сечении справедливо для участков, достаточно удаленных от мест: резкого изменения пло­щади поперечного сечения (рис. 3.7, в); скачкообразного изменения внешних нагрузок; скачкообразного изменения физико-механических характеристик конструкций.

Нормальные напряжения при сжатии определяют так же, как и при растяжении, но считают отрицательными.

 Следует помнить, что длинные (тонкие) стержни, нагруженные сжимающими силами, могут потерять устойчивость. Расчет стержней на устойчивость рассмотрен в разделе «Устойчивость». 

В инженерных сооружениях встречаются растянутые или сжатые элементы, имеющие отверстия. В сечениях с отверстием определяют осредненные нормальные напряжения по формуле



где    площадь поперечного сечения нетто; A - площадь поперечного сечения брутто;   - площадь его ослабления.

 

Деформации и перемещения. Закон Гука
Рассмотрим однородный стержень с одним концом, жестко за­деланным, и другим - свободным, к которому приложена централь­ная продольная сила Р (рис. 3.8). До нагружения стержня его длина равнялась l - после нагружения она стала равной   (рис. 2.8). Величину   называют абсолютной продольной деформацией (абсолютным удлинением) стержня. В большинстве случаев оно мало по сравнению с его первоначальной длиной l (∆l<<l).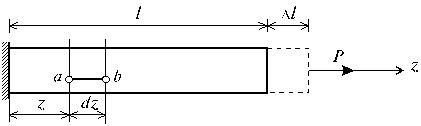



Рис. 3.8

 

Если в нагруженном стержне напряженное состояние является однородным, т.е. все участки стержня находятся в одинаковых ус­ловиях, деформация   остается одной и той же по длине стержня и равной



Величина ε называется относительной продольной деформацией.

Если же по длине стержня возникает неоднородное напряжен­ное состояние, то для определения его абсолютного удлинения не­обходимо рассмотреть бесконечно малый элемент длиной dz (рис. 3.8). При растяжении он увеличит свою длину на величину   и его деформация составит:



В пределах малых деформаций при простом растяжении или сжатии закон Гука записывается в следующем виде (нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформации  ):

Величина Е представляет собой коэффициент пропорциональ­ности, называемый модулем упругости материала первого рода (модуль продольной упругости). Его величина постоянна для каждого материала. Он характеризует жесткость материала, т.е. способность сопротивляться деформированию под действием внешней нагрузки.

Из совместного рассмотрения уравнений (2.5) и (2.6) получим:

откуда с учетом того, что



окончательно получим:



Если стержень изготовлен из однородного изотропного мате­риала с Е = const, имеет постоянное поперечное сечение A= const и нагружен по концам силой Р, то из (2.7) получим



Зависимость (2.8) также выражает закон Гука. Знаменатель  EA  называется жесткостью при растяжении - сжатии или продольной жесткостью.

При решении многих практических задач возникает необходи­мость, наряду с удлинениями, обусловленными действием механи­ческих нагрузок, учитывать также удлинения, вызванные темпера­турным воздействием. В этом случае пользуются принципом неза­висимости действия сил, и полные деформации рассматривают как сумму силовой и температурной деформаций:



где    коэффициент температурного расширения материала; t пе­репад температуры тела. Для однородного стержня, нагруженного по концам продольными силами Р и равномерно нагретого по длине, получим:



Потенциальная энергия деформации

Внешние силы, приложенные к упругому телу и вызывающие изменение геометрии тела, совершают работу W на соответству­ющих перемещениях. Одновременно с этим в упругом теле накап­ливается потенциальная энергия его деформирования U. При дей­ствии динамических внешних нагрузок часть работы внешних сил превращается в кинетическую энергию движения частиц тела К. Приняв энергетическое состояние системы до момента действия данных сил равным нулю, и в условиях отсутствия рассеивания энергии, уравнение баланса энергии можно записать в следующем виде:

W = U + K.                          (2.11)

При действии статических нагрузок К = 0, следовательно,

W = U.                                  (2.12)

Это означает, что при статическом нагружении работа внешних сил полностью преобразуется в потенциальную энергию деформа­ции. При разгрузке тела производится работа за счет потенциаль­ной энергии деформации, накопленной телом. Таким образом, уп­ругое тело является аккумулятором энергии. Это свойство упругого тела широко используется в технике, например, в заводных пружи­нах часовых механизмов, в амортизирующих рессорах и др. В слу­чае простого растяжения (сжатия) для вывода необходимых расчет­ных зависимостей потенциальной энергии деформации рассмотрим решение следующей задачи.

На рис. 3.9, а изображен растягиваемый силой Р стержень, удлинение которого соответствует отрезку  , ниже показан график изменения величины удлинения стержня    в зависимости от силы Р (рис. 3.9, б). В соответствии с законом Гука этот график носит линейный характер.

Пусть некоторому значению силы Р соответствует удлинение стержня  . Дадим некоторое приращение силе    соответству­ющее приращение удлинения составит  . Тогда элементарная работа на этом приращении удлинения составит: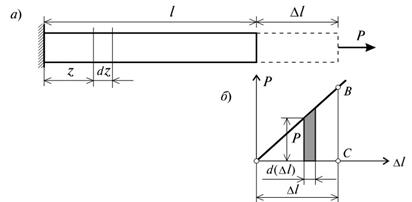





Рис. 3.9

               

вторым слагаемым, в силу его малости, можно пренебречь, и тогда



Полная работа равна сумме элементарных работ, тогда, при линейной зависимости “нагрузка  перемещение”, работа внешней силы Р на перемещении   будет равна площади треугольника ОСВ (рис. 3.9), т.е.



В свою очередь, когда напряжения   и деформации   распреде­лены по объему тела V равномерно (как в рассматриваемом случае) потенциальную энергию деформирования стержня можно записать в виде:



Поскольку, в данном случае имеем, что  , то



т.е. подтверждена справедливость (2.12).

С учетом (2.8) для однородного стержня с постоянным попе­речным сечением и при Р = const из (2.17) получим:



Единицей измерения потенциальной энергии деформации является 1Hм = 1Дж.

 

3.3. Расчеты на прочность и жесткость при растяжении-сжатии.
Основной задачей расчета конструкции является обеспечение ее безопасной эксплуатации. Важнейшим условием, обеспечивающим безопасную эксплуатацию конструкции, является условие прочности. Существуют различные методы обеспечения прочности конструкций. Мы чаще всего будем пользоваться одним из этих методов – расчетом по допускаемым напряжениям. Согласно этому методу для конструкций, работающих на растяжение-сжатие, условие прочности, составленное для опасного сечения,  можно записать в таком виде:



где   – максимальное напряжение в конструкции;   – характеристика материала, называемая допускаемым напряжением.

Допускаемое напряжение находится по формуле



где   – предельное напряжение, при достижении которого в стержне наступает предельное состояние материала: появляются пластические деформации, если материал стержня – пластичный, или происходит разрушение, если стержень выполнен из хрупкого материала; n – нормируемый коэффициент запаса прочности.

Кроме формулы (2.26), возможен второй вариант условия прочности





называется действительным коэффициентом запаса прочности, показывающим во сколько раз надо увеличить максимальное напряжение в стержне, чтобы материал стержня оказался в опасном (предельном) состоянии.

Условие прочности в зависимости от цели поставленной задачи позволяет выполнять расчеты на прочность двух видов: проектный и проверочный. Для спроектированного стержня можно также определять допускаемую нагрузку.

Проектный расчет выполняют с целью определения размеров поперечных сечений элемента конструкции при известных рабочих нагрузках и материале (допускаемых напряжений). Площадь поперечного сечения определяют из выражения



Форма сечения стержня не влияет на его прочность при растяжении (сжатии). Форму сечения стержня необходимо знать только для определения размеров сечения при известном значении площади.

Зная площадь сечения и его форму, находят размеры сечения.

Проверочный расчет выполняют для спроектированной конструкции с целью проверки ее прочности. При проверочном расчете должны быть известны площадь опасного сечения, нагрузка и материал (допускаемое напряжение). Проверочный расчет выполняют по формуле (2.26).

Определение допускаемой нагрузки для спроектированного элемента конструкции, размеры поперечного сечения которого и материал (допускаемые напряжения) известны. Условие прочности в этом случае записывают в виде



Зная значение  , определяют допускаемую нагрузку  .

Так как допускаемые напряжения не имеют точного значения, а выбираются приближенно, то при проверочном расчете максимальные рабочие напряжения могут превышать допускаемые на 5%. По этой же причине можно округлять полученные в расчетах значения площади опасного поперечного сечения или допускаемой нагрузки так, чтобы максимальные напряжения отличались от допускаемых не более чем на 5%. По этой же причине можно округлять полученные в расчетах значения площади опасного поперечного сечения или допускаемой нагрузки та, чтобы максимальные напряжения отличались от допускаемых не более чем на 5%.

При проектировании элементов конструкций стремятся сделать их во всех сечениях равнопрочными.

Рассмотренные три вида расчетов на прочность можно выполнять не только при растяжении или сжатии, а при любом виде деформации (сдвиге, кручении, изгибе).

При проектировании строительных конструкций расчет на прочность стальных элементов, подверженных центральному растяжению или сжатию, следует выполнять по формуле



где  – коэффициент условий работы, принимаемый по СНИП (см. табл. 3.1) или другим нормам.

 

Таблица 3.1

Элементы конструкции
Колонны общественных зданий и опор водонапорных башен Элементы стержневых конструкций покрытий и перекрытий: а) сжатых при расчетах на устойчивость б) растянутых в сварных конструкциях Сплошные составные балки, колонны, несущие статическую нагрузку и выполненные с помощью болтовых соединений, при расчетах на прочность Сечения прокатных и сварных элементов, несущих статическую нагрузку, при расчетах на прочность Сжатые элементы из одиночных уголков, прикрепляемые одной полкой	0,95   0,95 0,95   1,1   1,1 0,75
Примечание: В случаях, не оговоренных в настоящих нормах, в формулах следует принимать   .

                                             

 Для хрупких строительных материалов условия прочности принимают вид:

при растяжении:



при сжатии:



где   и   – допускаемые напряжения при растяжении и сжатии; n_t и n_c – нормативные коэффициенты запаса прочности по отношению к пределу прочности (n_t, n_c>1).

Для центрально сжатых бетонных элементов формула (2.33) записывается в виде:



где   – коэффициент, принимаемый для бетона тяжелого, мелкозернистого и легкого равным 1,00; для ячеистого автоклавного – 0,85; для ячеистого неавтоклавного – 0,75.

В некоторых случаях работоспособность элемента конструкции определяется не только его прочностью, но и жесткостью, т.е. способностью элемента воспринимать нагрузки без недопустимых упругих деформаций. При расчетах на жесткость определяют максимальные перемещения сечений и сопоставляют их с допускаемыми перемещениями.

Условие жесткости, ограничивающее изменение длины элемента, имеет сле­дующий общий вид:

где    - изменение размеров детали;

[ ] - допускаемая величина этого изме­нения.

Учитывая, что при растяжении (сжатии) абсолютное удлинение в общем виде определяется как алгебраическая сумма величин    по участкам



условие жесткости при растяжении (сжатии) запишем следующим образом:



Так как перемещение, согласно закону Гука, зависит от нагрузки и размеров поперечного сечения, условие жесткости позволяет решать те же три вида задач, что и условие прочности.  

 

3.4. Расчеты статически определимых стержней
Статически определимый стержень – это стержень, который можно рассчитать, используя только уравнения равновесия (уравнения статики).

В любой науке, которая называется «точной» и в которой используются аналитические методы описания состояний и явлений, не обойтись без моделей. В нашем случае при решении различных задач мы каждый раз будем выбирать для рассматриваемого объекта расчетную схему.

Расчетная схема – это упрощенная схема конструкции или ее элементов, освобожденная от несущественных в данной задаче особенностей. При этом расчетная схема должна отражать все наиболее существенное для характера работы данной конструкции и не содержать второстепенных факторов, мало влияющих на результаты ее расчета. Построение и обоснование расчетной схемы – ответственный этап проектирования и расчета конструкции.

Перейдем к рассмотрению конкретных примеров.

 

Пример 5.

Чугунная труба-стойка высотой H=l=3м с наружным диаметром D=25 см и внутренним диаметром d=20 см нагружена сжимающей силой F=50 т, модуль упругости чугуна  . Найти напряжение   в поперечном сечении колонны, абсолютное    и относительное укорочения  .

Решение.

Как уже говорилось выше, решение задачи начинается с выбора расчетной схемы. В данном случае стойка изображается как вертикальный стержень длиной H=l=3м, жестко закрепленный в нижней части (условное изображение фундамента или земли). К верхней части стержня приложена сосредоточенная сжимающая сила (направление к стержню). При этом линия действия силы должна совпадать с осью стержня. Кроме того, рядом необходимо изобразить поперечное сечение стойки с указанием основных размеров. В данном примере – это кольцо. Расчетная схема для решения задачи изображена на рис. 3.10, а.

Далее строим эпюру продольной силы и определяем максимальное внутреннее усилие, возникающее в колонне. Поскольку внешняя нагрузка постоянна по высоте, то возникает только одна сжимающая

продольная сила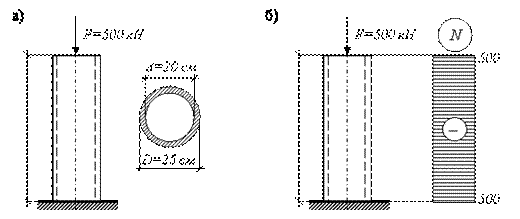   



Рис. 3.10

 

Максимальное нормальное напряжение   определяется по формуле:



где A [м²]– площадь трубы:



тогда:



Абсолютное и относительное укорочения стойки определяем по формулам:





Знак "минус" обозначает уменьшение размера (укорочение).

3.5. Понятие о статически неопределимых системах

Основные положения. Связи необходимые и дополнительные.

Для решения задач сопротивления материалов необходимо знать все внешние силы, действующие на конструкцию, включая реакции наложенных на нее связей. Из теоретической механики известно, что для равновесия твердого тела, нагруженного плоской системой сил, достаточно наложить на тело три связи, а нагруженного пространственной системой сил – шесть связей. Соответственно для таких систем можно составить три и шесть независимых уравнений равновесия. Если при рассмотрении заданной системы, находящейся в рав­новесном состоянии от действия заданных внешних нагрузок, все реакции в связях закрепления можно определить с помощью уравнений равновесия, без использо­вания дополнительных условий, то такая система называется ста­тически определимой.

В реальной практике встречаются такие конструкции, при рас­чете которых одних лишь уравнений равновесия оказывается не­достаточно, в связи с чем требуется формулирование дополнитель­ных уравнений, связанных с условиями деформирования конструк­ции.

Системы, в которых количество наложенных связей больше, нежели число независимых уравнений равновесия, называются статически неопределимыми.

В машиностроении и строительных конструкциях такие системы на­ходят широкое применение. В одних случаях статическая неопределимость является сущностью самой конструкции.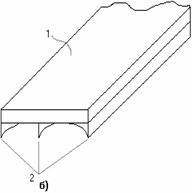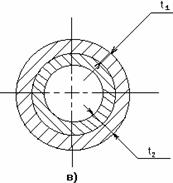

  

Рис. 3.11.

 

Примерами таких конструкций могут быть: армированные уголками стойки (рис.3.11, а); панель крыла самолета, состоящая из обшивки 1 с продольными ребрами 2 (рис. 3.11, б); составной цилиндр, полученный пу­тем напряженной посадки двух труб из различных материалов (рис. 3.11, в). В других случаях, с целью повышения жесткости и надежности сис­темы, вводятся дополнительные связи сверх тех минимально необходи­мых, которые обеспечивают ее кинематическую неизменяемость. Нало­жение на систему дополнительных связей превращает ее в статически неопределимую. Напомним, что кинематическая неизменяемость пло­ской системы обеспечивается тремя, а пространственной – шестью свя­зями.

Конструкции, состоящие из стержней, соединенных шарнирами, называются шарнирно-стержневыми. В этих конструкциях есть стержни, которые обеспечивают геометрическую неизменяемость конструкции и при удалении которых система превращается в механизм. Такие стержни будем называть необходимыми. Если же при удалении некоторых стержней геометрическая неизменяемость конструкции не нарушается, то такие стержни назовем лишними. Лишними такие связи называются только потому, что они не являются необходимыми для обеспечения равновесия конст­рукции и ее геометрической неизменяемости, хотя постановка их дикту­ется условиями эксплуатации. По условиям прочности и жесткости кон­струкции лишние связи могут оказаться необходимыми.

В статически определимой системе есть только необходимые стержни, в статически неопределимой – число лишних стержней равно степени статической неопределимости.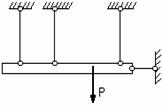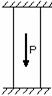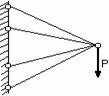

                                           

                             а)                                               б)                                        в)

Рис. 3.12

 

На рис. 3.12 приведены схемы 3-х плоских систем с «лишними» связями: а – стержневой подвески; б – стержня, закрепленного обоими концами; в – стержневого кронштейна. В схеме, показанной на рис. 3.12, в, вся система состоит из упругих звеньев. Подсчет числа наложенных связей произво­дится в этом случае следующим образом. Каждый стержень связан с опорной поверхностью двумя связями. Всего таких связей 8. Шарнир, соединяющий концы стержней, снимает связи, ограничивающие относи­тельный или взаимный их поворот. При соединении двух стержней од­ним шарниром снимается одна связь, трех стержней – две связи, четырех – три и т.д. В данном случае снимаются три связи. Следовательно, всех связей, наложенных на эту систему оказывается пять, две из которых мо­гут считаться «лишними».

Статически неопределимые конструкции характеризуются рядом осо­бенностей, по сравнению со статически определимыми системами. За­ключаются они в том, что в элементах статически неопределимых систем напряжения возникают не только от действия внешних сил, но и в ре­зультате изменения температуры, неточности изготовления деталей, не­точностей их сборки, смещения мест опорных креплений и ряда других причин. Объясняется это тем, что деформация одного из элементов в статически неопределимой системе приводит к деформа­ции и других ее элементов.

Например, если один из стержней системы (рис. 3.12, в) изготовлен по длине неточно, то соединение концов стержней одним шарниром возможно только путем деформации всех стержней.

Сила, возникающая при деформации одного из стержней, вызывает усилия в других стержнях, находящихся с ним в шарнирном соединении. Смонтированная система приходит в равновесие, следовательно, сово­купность сил системы обеспечивает ее равновесие. Эти силы вызывают соответствующие, называемые начальными, напряжения в стержнях.

В статически неопределимых конструкциях при изменении темпера­туры ее элементов по сравнению с температурой, при которой осуществ­лялась сборка, возникают дополнительные усилия и напряжения, кото­рые принято называть температурными.

Распределение усилий между элементами системы зависит от их же­сткости. Если увеличить жесткость какого- либо элемента, то он примет на себя большее усилие. Изменяя соотношение жесткостей элементов конструкций, можно менять распределение усилий между ними.

Эти особенности статически неопределимых конструкций должны учитываться при проектировании или применении таких систем.

Статически неопределимые системы обладают повышенной «живуче­стью». Разрушение одного или нескольких элементов (в зависимости от числа дополнительных связей) не вызывает потерю несущей способности конструкции в целом. Так разрушение даже двух стержней в системе, показанной на рис. 3.12, в не приводит к потере способности восприни­мать силу P оставшимися двумя стержнями, конечно, при условии их достаточной прочности.

 

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

- Что называется стержнем?

- Какой вид нагружения стержня называются осевым растяжением (сжатием)?

- Какие внутренние силовые факторы возникают в сечении бруса при растяжении и сжатии?

- Дайте определение эпюры внутреннего силового фактора.

- Какой вид нагружения стержня называется растяжением (сжатием)?

- Что называют нормальной силой?

- Как определяется значение нормальной силы в поперечном сечении?

- Какие нагрузки называют распределенными? Указать размерности различных внешних сил (в системе СИ).

- Как вычисляется значение продольной силы N в произвольном поперечном сечении бруса?

- Что представляет собой эпюра продольных сил и как она строится?

- Как распределены нормальные напряжения σ_х в поперечных сечениях центрального растянутого бруса и чему они равны?

- В каких сечениях растянутого бруса возникают наибольшие нормальные напряжения?

- Что называется жесткостью поперечного сечения  при растяжении?

- Как формулируется закон Гука? Запишите формулы абсолютной  и относительной продольной деформации бруса?

- Что представляют собой эпюра продольных перемещений?

- В чем смысл и какова формула поверочного расчета?

- Как назначаются допускаемые напряжения для пластичных и хрупких материалов?

- Как выполняется проектировочный расчет?

- Почему необходимо выполнять условие жесткости? Приведите примеры.

- Как вычисляется значение продольной силы в произвольном поперечном сечении стержня?

- Какого характера напряжения возникают в поперечном сече­нии при растяжении и сжатии: нормальные или касательные?

- Как распределены нормальные напряжения в поперечных сечениях центрально-растянутого или центрально-сжатого стержня и по какой формуле они определяются?

- В каких единицах измеряется напряжение?

- Как назначаются знаки продольной силы и нормального на­пряжения?

- Как связаны гипотеза плоских сечений (гипотеза Бернулли) и закон распределения нормальных напряжений в поперечном сечении растянутого (сжатого) стержня?

- Раскройте понятие эпюр продольных сил, нормальных напряжений и перемещений. Для чего они строятся? Каких правил придерживаются при построении эпюр?

- Что показывает эпюра продольной силы?

 Что представляют собой эпюры внутренних силовых факторов? С какой целью их строят?

- Опишите технику построения эпюры продольных сил в брусе, загруженном несколькими сосредоточенными силами по оси бруса?

- Как вычислить значение продольной силы в произвольном поперечном сечении бруса?

- Как вычислить напряжения в поперечном сечение бруса при растяжении и сжатии? Как они распределены по поперечному сечению?

- Как определяют абсолютное удлинение ступенчатого бруса, нагруженного несколькими силами?

- Как определяется удлинение призматического бруса от собственного веса?

- Какое влияние оказывает собственный вес стержня при проектирования сооружения?

- Что понимается под брусом равного сопротивления?

- Запишите формулы для определения удлинения бруса. Что характеризует произведение АЕ и как оно называется?

- Какие деформации бруса называются абсолютными и какие относительными?

- Что называется удлинением стержня (абсолютной продольной деформацией)? Что такое относительная продольная деформация? Каковы размерности абсолютной и относительной продольных деформаций?

- Опишите технику определения продольных и поперечных деформаций бруса при растяжении-сжатии?

- Стальной стержень длиной 1,5 м вытянулся под нагрузкой на 3 мм. Чему равно относительное удлинение? Чему равно относительное сужение? ( = 0,25)

- Что характеризует модуль упругости материала? Какова единица измерения модуля упругости?

- Что называется модулем упругости Е? Как влияет величина Е на деформации стержня?

- Что называется жесткостью поперечного сечения стержня при растяжении (сжатии)?

- Относительные деформации и перемещения.

- Что понимается под жесткостью при растяжении или сжатия стержня?

- Принципы расчета на жесткость.

- Типы задач при расчетах на жесткость.

- Примеры влияния жёсткости на работоспособность конструкции.

- Сформулируйте закон Гука. Напишите формулы для абсолютной и относительной продольных деформаций стержня.

- Что происходит с поперечными размерами стержня при его растяжении (сжатии)?

- Что характеризует коэффициент поперечной деформации?

- Что такое коэффициент Пуассона? В каких пределах он изменяется?

- Как определяется коэффициент Пуассона?