24.05.05 Прикладная механика.. Учебное пособие по дисциплине Механика Модуль Прикладная механика

• Название: Учебное пособие по дисциплине Механика Модуль Прикладная механика
• Дата: 17.04.2023
• Размер: 1.89 Mb.
• Имя файла: 24.05.05 Прикладная механика..docx
• Тип: Учебное пособие; #1068488
• страница: 16 из 18

Рис. 9.17. Дифференциальный механизм

 

К зубчатым передачам относятся и устройства прерывистого движения: храповые механизмы, мальтийские механизмы и другие.

 

Храповые механизмы
Храповые механизмыотносятся к механизмам прерывистого действия, которые обеспечивают движения ведомого звена в одном направлении с периодическими остановками. Конструк­тивно храповые механизмы делятся на не­реверсивные с внутренним зацеплением и с храповым колесом, а также реверсивные в виде зубчатой рейки.

Нереверсивный храповый механизм с внутренним зацеплением (рис. 9.18).Веду­щим звеном может быть как храповое ко­лесо внутреннего зацепления 1, соединен­ное с зубчатым колесом внешнего зацепле­ния, так и втулка 4 с закрепленной на ней собачкой 3, подпружиненной к зубьям храпового колеса 1 пружиной 2.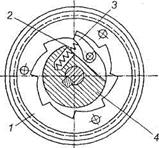


Рис. 9.18. Нереверсивный храповый механизм с внутренним зацеплени­ем:

1 — храповое колесо; 2 — пру­жина; 3 — собачка; 4 — втулка
В нереверсивных механизмах (рис. 9.19) храповое колесо выполняют в виде рейки 1 в направляющих, и тогда собачка 2 сообщает рейке с храпо­вым зубом прерывистое прямолинейное движение. В этом случае преду­сматривает устройство, которое возвращает рейку в начальное положение.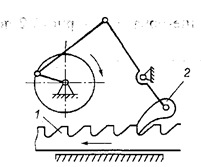



Рис. 9.19. Нереверсивный храповый механизм:           

1 - рейка; 2 - собачка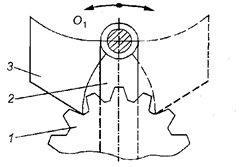                                            

 



Рис. 9.20. Реверсивный храповый механизм:

1- храповик; 2 - ведущий рычаг; 3 - собачка

 

Реверсивные храповые механизмы (рис. 9.20) имеют: храповое колесо 1 с  зубьями эвольвентного профиля, а на ведущем рычаге 2 шарнирно устанав­ливают собачку 3,  которую при необходимости реверса перебрасывают во­круг оси О_х.
Механизмы с гибкими звеньями
Ременные передачи

Механизмы с гибкими звеньями применяются при значительных межосевых расстояниях.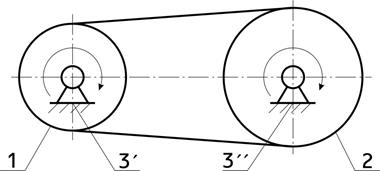 

 



 

Рис. 9.21.  Открытая ременная передача

 

На рис.9.21 показан простейший пример открытой ременной передачи, у которой вращение шкивов 1 и 2происходит в одном и том же направлении.

Передача ремнем осуществляется за счет трения возникающего между шкивом и ремнем. Ременьможет быть плоский, клиновойили зубчатый.

Все механические передачи характеризуются передаточным числом или отношением. Рассмотрим работу двух элементов передачи, один из которых будет ведущим, а второй — ведомым.

Введем следующие обозначения: ω₁ и п₁ — угло­вая скорость и частота вращения ведущего вала, выраженные соответственно рад/с и об/мин; ω₁ и п₂ — угловая скорость и частота вращения ведомого вала; D₁и D₂ - диаметры вращающихся деталей (шкивов, катков и т. п.); v₁ и v₂ — окружные скоро­сти, м/с.

Отношение диаметров ведомого элемента пере­дачи к ведущему называют передаточным числом



Если известны параметры передачи — диаметры D₁и D₂или числа зубьев z₁и z₂, передаточное число и определяем следующим образом.

Для зубчатых передач передаточное число и — отношение числа зубьев ведомого колеса к числу зубьев ведущего колеса, т.е. и = z₂/z₁, где z₂и z₁ — числа зубьев соответственно ведомого и ведущего колеса.

Итак, передаточное число



 (обратите внимание на индексы у букв ω, п, D и z); u=D₂/D₁ относится к фрикционной передаче без учета скольжения.

Отношение угловых скоростей ведущего ω₁  и ведомого ω₂ звеньев называют также передаточным отношением и обозначают  і.

В передаче, понижающей частоту вращения n (угловую скорость ω), u>1; при и<1 частота вращения (угловая скорость) повышается. Понижение частоты вращения называют редуцированием, а закрытые передачи, понижающие частоты вращения,– редукторами. Устройства, повышающие частоты вращения, называют ускорителями или мультипликаторами. Передачи выполняют с постоянным, переменным или регулируемым передаточным отношением. Изменение передаточного отношения может быть ступенчатым(коробка передач) и бесступенчатым(вариаторы).

 В приводах с большим передаточным числом (до и= 1000 и выше), со­ставленных из нескольких последовательно соединенных передач (много­ступенчатые передачи), передаточное число равно произведению переда­точных чисел каждой ступени передачи, т. е.



Передача мощности от ведущего вала к ведомому всегда сопровожда­ется потерей части передаваемой мощности вследствие наличия вредных со­противлений (трения в движущихся частях, сопротивления воздуха и др.).

Если Р₁ — мощность на ведущем валу, Р₂— на ведомом валу, то Р₁> Р₂.

Отношение значений мощности на ведомом валу к мощности на веду­щем валу называют механическим коэффициентом полезного действия (КПД) и обозначают буквой η:



Общий КПД многоступенчатой последовательно соединенной переда­чи определяют по формуле



где    — КПД, учитывающие потери в отдельных кинематических парах передачи.

КПД характеризует качество передачи. Потеря мощности – показатель непроизводительных затрат энергии – косвенно характеризует износ деталей передачи, так как потерянная в передаче мощность превращается в теплоту и частично идет на разрушение рабочих поверхностей.

С уменьшением полезной нагрузки КПД значительно снижается, так как возрастает относительное влияние постоянных потерь (близких к потерям холостого хода), не зависящих от нагрузки;


9.3. Структура механизмов.
Понятие о структурном синтезе и анализе
Задачей структурного анализа является задача определения параметров структуры заданного механизма - числа звеньев и структурных групп, числа и вида КП, числа подвижностей (основных и местных), числа контуров и числа избыточных связей.

Задачей структурного синтеза является задача синтеза структуры нового механизма, обладающего заданными свойствами: числом подвижностей, отсутствием местных подвижностей и избыточных связей, минимумом числа звеньев, с парами определенного вида (например, только вращательными, как наиболее технологичными) и т.п.

Степень свободы и классы кинематических пар

Соединение двух соприкасающихся звеньев, допускающее их относительное движение, называется кинематической парой.

Совокупность поверхностей, линий и отдельных точек звена, по которым оно может соприкасаться с другим звеном, образуя кинематическую пару, называется  элементом кинематической пары.

Если звенья подвижно соединяются в нескольких местах, то кинематическая пара является разветвленной, а отдельные части этого соединения называются ветвями кинематической пары. 

Для абсолютно твердого тела, свободно движущегося в пространстве  пространстве (в декартовой системе координат X, Y, Z), число независимых параметров, определяющих его положение в пространстве или число степеней свободы, равно шести (рис.22): три возможных перемещения вдоль неподвижных координатных осей X, Y и Z и три возможных вращения вокруг этих осей.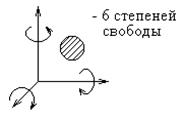

 



Рис. 9.22. Степени свободы тела в пространстве

 

Для звеньев, вошедших в кинематическую пару, число степеней свободы всегда меньше шести, так как кинематическая пара уменьшает число возможных перемещений и накладывает число условий связи S на относительное движение каждого звена, зависящих от способа соединения звеньев в пары. В таком случае число степеней свободы H  кинематической пары равно

H = 6 − S.                            (1)

Все кинематические пары делятся на классы в зависимости от числа условий связи, налагаемых ими на относительное движение звеньев. Так как число условий связи может быть от одного до пяти, то число классов пар равно пяти. В соответствии с этим имеем кинематические пары I −V классов. Например, если телами (звеньями), образовавшими кинематическую пару, утрачено по 5 степеней свободы каждым, эту пару называют кинематической парой 5-го класса. Если утрачено 4 степени свободы – 4-го класса и т.д. (рис. 9.22). При S=0 пары не существует, а есть два тела, движущихся независимо друг от друга. При S=6 кинематическая пара становится жестким соединением двух звеньев, т.е. одним звеном.

Класс кинематической пары может быть определен из зависимости (1):

S = 6 – H.                        (2)

 

Классификация кинематических пар
Кинематические пары (КП) классифицируются по следующим признакам:

1) по виду места контакта (места связи) поверхностей звеньев:

- низшие, в которых контакт звеньев осуществляется по плоскости или поверхности (пары скольжения). К низшим парам относятся: вращательная, поступательная, винтовая, цилиндрическая, сферическая, плоскостная и т.п. (Пример низшей кинематической пары: два цилиндра, находящиеся в постоянном соприкосновении, из которых один вращается внутри другого).

- высшие, в которых контакт звеньев осуществляется по линиям или точкам (пары, допускающие скольжение с перекатыванием). Они имеются, например, в зубчатых и кулачковых механизмах. При этом линейный или точечный контакт понимается как первоначальный - при соприкосновении звеньев без усилия, а под нагрузкой звенья, образующие высшую пару, будут соприкасаться по некоторой фактической поверхности, называемой пятном контакта.

 



Рис. 9.23
Преимуществом низших кинематических пар по сравнению с высшими является возможность передачи больших нагрузок, поскольку контактная поверхность соприкасающихся звеньев низшей пары может быть весьма значительной, имеют большие потери на трение, сложнее синтезируются. Имеют простые формы в виде плоскостей, цилиндрических поверхностей, поэтому более технологичны, т. е. просты в изготовлении.

 

Таблица 9.1. 

Условные обозначения кинематических пар

Класс пары	Число условий связи	Число степеней свободы	Название пары	Рисунок	Условное обозначение
I	1	5	Шар-плоскость
II	2	4	Шар-цилиндр
III	3	3	Сферическая
III	3	3	Плоскостная
IV	4	2	Цилиндрическая
IV	4	2	Сферическая с пальцем
V	5	1	Поступательная
V	5	1	Вращательная
V	5	1	Винтовая

Кинематической цепью называется система звеньев, связанных между собой кинематическими парами.

Механизм − это кинематическая цепь, в которой при заданном движении одного или нескольких звеньев относительно одного из них все остальные звенья совершают однозначно определяемые движения.
Степень свободы и структурная формула механизма
Число степеней свободы механизма – это число степеней свободы всей кинематической цепи относительно неподвижного звена (стойки).

Если на движение звена в пространстве не наложено никаких условий связи, то оно обладает шестью степенями свободы. Тогда если число звеньев кинематической цепи равно к, то общее число степеней свободы, которым обладают к звеньев до их соединения в кинематические пары, равно 6к. Соединение звеньев в кинематические пары накладывает различное число условий связи S на относительное движение звеньев, зависящее от класса пар.

Если число пар I класса, у которого S₁=1, а H₁=5, в которые входят звенья рассматриваемой кинематической цепи, равно р₁, число пар II класса, у которого S₁=2, а H₁=4 – р₂, число пар III класса, у которого S₁=3, а H₁=3 – р₃, число пар IV класса, у которого S₁=4, а H₁=2 – р₄, число пар V класса, у которого S₁=5, а H₁=1 – р₅, то из 6к степеней свободы, которыми обладали звенья до вхождения в кинематические пары, необходимо исключить те степени свободы, которые отнимаются вхождением звеньев в кинематические пары. Тогда число степеней свободы Н кинематической цепи равно

Н = 6к - 5р₅ - 4р₄ - 3р₃ - 2р₂ – р₁.                           (3)

Формула (3) − это формула подвижности или структурная формула кинематической цепи общего вида. Данная формула называется формула Малышева, получена П.И. Сомовым в 1887 году и развита А.П. Малышевым в 1923 году.

Число степеней свободы W механизма относительно неподвижного звена будет равно

W = H – 6  или  W = 6(к-1) - 5p₅ - 4p₄ - 3p₃ - 2p₂ – p₁

или                 

W = 6n -5p₅ - 4p₄ - 3p₃ - 2p₂ – p₁,                          (4)

где n=k-1 − число подвижных звеньев кинематической цепи. Формула (4) носит название формулы подвижности, или структурной формулы механизма общего вида.

Величина W показывает, сколько должно быть у механизма ведущих звеньев (если W = 1 – одно, W = 2 – два ведущих звена и т.д.).

Когда три связи уже наложены условием параллельности осей, структурная формула будет такой:

W = (6-3)n - (5-3)p₅ - (4-3)p₄ - (3-3)p₃,

или

W = 3n - 2p₅ – p₄.                           (5)

Формула (5) есть структурная формула для плоских механизмов общего вида. Формулу (5) называют также формулой П.Л. Чебышева (1869). Она может быть получена из формулы Малышева при условии, что на плоскости тело обладает не шестью, а тремя степенями свободы.

Показательным в этом отношении является пример зубчатого механизма планетарного типа, изображённый на рис. 9.24.

В состав механизма входит центральное колесо 1, являющееся ведущим, три параллельно работающих  сателлита 2 и стержневое звено 3, образующее вращательные пары с сателлитами. Все подвижные звенья размещены внутри неподвижного колеса 0 с внутренними зубьями. Данные для расчёта таковы: количество пар 5-го класса p₅=5 (они на схеме отмечены римскими цифрами), каждый  сателлит 2 образует зацепление (две кинематические пары) с колёсами 0 и 1, поэтому p₄=6, количество подвижных звеньев механизма n=5, количество степеней свободы механизма W=1.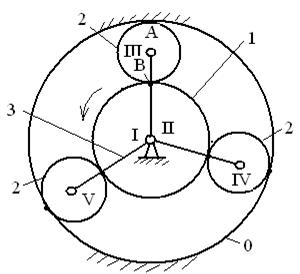