24.05.05 Прикладная механика.. Учебное пособие по дисциплине Механика Модуль Прикладная механика

• Название: Учебное пособие по дисциплине Механика Модуль Прикладная механика
• Дата: 17.04.2023
• Размер: 1.89 Mb.
• Имя файла: 24.05.05 Прикладная механика..docx
• Тип: Учебное пособие; #1068488
• страница: 13 из 18

7.1.Расчет балки, подверженной косому или пространственному изгибу

Косым называют изгиб, при котором плоскость действия изгибающего момента, возникающего в сечении, не совпадает ни с одной из главных плоскостей бруса (при этом плоскость действия изгибающего момента обязательно должна проходить через центр тяжести сечения) (рис.7.4).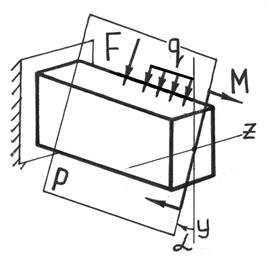



Рис.7.3

 

При косом изгибе изогнутая ось представляет собой плоскую кривую, и плоскость, в которой она расположена, не совпадает с плоскостью действия нагрузки.

При пространственном изгибе нагрузка приложена в разных плоскостях, деформированная ось является пространственной кривой.

Определение внутренних усилий при косом изгибе
При косом изгибе в поперечных сечениях бруса действуют следующие внутренние усилия: M_z, M_y – изгибающие моменты и Q_y, Q_z –поперечные (перерезывающие) силы. Это легко показать мысленно рассекая стержень и определяя внутренние усилия при косом изгибе консольной балки под действием сосредоточенной силы F на свободном конце (см. рис.7.4):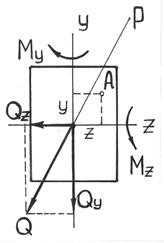








Рис. 7.4

 

Правило знаков для внутренних усилий: изгибающие моменты – положительны, если вызывают растяжение в положительном квадранте координатной системы zOy; поперечные силы – положительны, если под их действием отсеченный элемент поворачивается по часовой стрелке.

Таким образом, косой изгиб может быть представлен как совместное действие двух плоских изгибов в двух взаимно перпендикулярных плоскостях инерции.

Для определения полного изгибающего момента M и полной поперечной силы Q при косом изгибе достаточно определить внутренние усилия для каждого из плоских изгибов в отдельности (то есть Q_y, M_z и Q_z, M_y), а затем найти их векторную сумму:





 

Определение напряжений при косом изгибе
Если разложить внешние силы по главным осям инерции Ох и Оу, то получим две системы сил P_1x, P_2x, …, P_nx и P_1y, P_2y,..., P_ny, каждая из.которых вызывает прямой изгиб с изгибающими моментами соответственно M_y и М_x(рис.7.6). Применяя принцип независимости действия сил, нормальные напряжения   (рис.7.7) определим как алгебраическую сумму напряжений от M_x и М_y:

7.2. Изгиб с растяжением (сжатием)

Если нагрузить брус в главной плоскости силой F (рис. 7.5,а) под углом α к оси, то в поперечном сечении 1-1 (рис. 7.5,б) возникнут два внутренних силовых фактора: нормальная сила N =F∙cosα и изгибающий момент M_z = F∙xsinα. Следовательно, такое нагружение бруса вызывает сочетание изгиба с растяжением (сжатием).

Считая, что брус обладает большой жесткостью при изгибе (малые величины прогиба бруса), согласно принципу независимости действия сил, можно утверждать, что в любом сечении возникают напряжения растяжения (сжатия):

и напряжения изгиба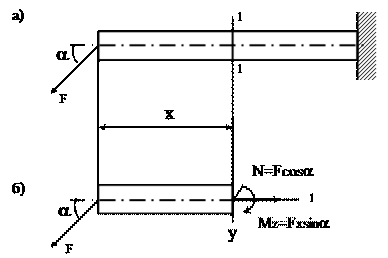




Рис. 7.5

 

Считая, что брус обладает большой жесткостью при изгибе (малые величины прогиба бруса), согласно принципу независимости действия сил, можно утверждать, что в любом сечении возникают напряжения растяжения (сжатия):

и напряжения изгиба



Таким образом, суммарные напряжения в любом сечении бруса находят алгебраическим сложением напряжений σ_N  и σ_MZ:



При расчетах на прочность исходят из наибольших напряжений, возникающих в любом сечении. В частности, если сечение бруса симметрично относительно нейтральной оси, то



Необходимо учитывать, что в последних двух формулах значения напряжений берутся со  своими знаками плюс или минус.

7.3. Внецентренное сжатие или растяжение
Вторым практически важным случаем сложения деформаций от изгиба и от продольных сил является так называемое внецентренное сжатие или растяжение, вызываемое одними продольными силами. Этот вид нагружения довольно распространен в технике, так как в реальной ситуации почти невозможно приложить растягивающую нагрузку точно в центре тяжести.

Внецентренным растяжением-сжатием называется случай, когда равнодействующая сил, приложенных к отброшенной части стержня, направлена параллельно оси стержня, но не совпадает с этой осью (рис.7.6).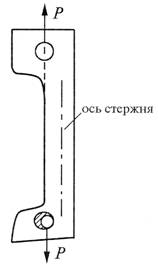



Рис.7.6

 

Представим, что после проведения разреза равнодействующая Р сил действующих на отброшенную часть и приложенная к оставшейся проходит через точку с координатами (x_p; y_p) в главных центральных осях поперечного сечения (рис. 7.7).

центральных осях поперечного сечения (рис. 7.8).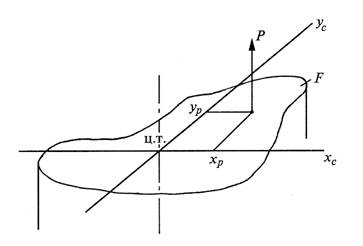



Рис.7.7

 

Приведем силу Р в центр тяжести сечения, т.е. направим вдоль оси стержня (сила N). При этом появятся две пары сил   относительно главных центральных осей (рис.7.8).

Таким образом, в поперечном сечении стержня при внецентренном растяжении и сжатии возникают три внутренних силовых фактора: нормальная сила N и два изгибающих момента   относительно главных центральных осей поперечного сечения.

Для вычисления нормального напряжения в поперечном сечении в окрестности точки с произвольными координатами x,y воспользуемся принципом независимости действия сил. Будем вычислять нормальное напряжение от каждого внутреннего силового фактора в отдельности и результат сложим.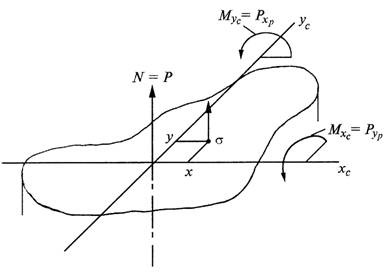




Рис.7.8
7.4. Критерии предельного состояния материала при сложном напряженном состоянии.

Теории прочности. Гипотезы (теории) прочности
Критерии разрушения или гипотезы прочности представляют собой предположения о преимущественном влиянии на прочность материалов того или иного фактора, сопутствующего процессу деформации и разрушения материалов.

Наиболее важными факторами, связанными с возникновением опасного состояния материала, являются: нормальные и касательные напряжения, линейные деформации и потенциальная энергия деформации.

При сложном напряженном состоянии следует говорить не о предельном напряжении, а о предельном напряженном состоянии. В качестве предельного состояния в опасной точке детали принимается переход материала в окрестности данной точки из упругого состояния в пластическое или разрушение детали, выражающееся в образовании трещин.

Теория наибольших нормальных напряжений (I теория прочности, Галилей, 1638 г.)

В основу теории наибольших нормальных напряжений положена гипотеза о преимущественном влиянии наибольших по абсолютной величине нормальных напряжений.

Согласно данной теории прочности опасное состояние материала при сложном напряженном состоянии наступает тогда, когда наибольшее из главных напряжений достигает величины, соответствующей пределу прочности при простом растяжении.

В этом случае условие прочности должно иметь вид:

 - при растяжении,                                                                           (14)

  - при сжатии.                                                                               (15)

Данная гипотеза удовлетворительно согласуется с результатами испытания деталей из хрупких материалов, таких как камень, кирпич, чугун. Для расчета деталей из пластичных материалов данная гипотеза непригодна.

 

Теория наибольших линейных деформаций (II теория прочности, Мариотт, 1682 г.)

В основу теории наибольших линейных деформаций положена гипотеза о преимущественном влиянии наибольших по абсолютной величине линейных деформаций.

Согласно данной теории прочности опасное состояние материала при сложном напряженном состоянии наступает тогда, когда наибольшее из относительных удлинений достигает опасной величины, соответствующей пределу прочности при простом растяжении.

Опыты этого не подтверждают. В связи с этим данная теория для расчета деталей не используется.

Теория наибольших касательных напряжений (III теория прочности; Кулон, 1773 год)

В основу теории наибольших касательных напряжений положена гипотеза о преимущественном влиянии наибольших по абсолютной величине касательных напряжений.

Согласно данной теории прочности опасное состояние материала при сложном напряженном состоянии наступает тогда, когда наибольшее из касательных напряжений достигает величины, соответствующей пределу текучести при простом растяжении.

Предельное значение максимальных касательных напряжений при растяжении



Сравнивая с условием наступления предельного состояния (13), получим эквивалентное напряжение по III теории прочности:

На практике встречаются случаи, когда σ_y =0, тогда



Условие прочности (31) хорошо согласуется с результатами испытания изотропных материалов, поэтому данная теория широко применяется для расчета деталей из металлических материалов.

 

Теория наибольшей удельной потенциальной энергии формоизменения (IV теория прочности; Бельтрами - 1885 г.; Губер - 1904 г.)

В основу энергетической теории прочности положена гипотеза о преимущественном влиянии удельной потенциальной энергии изменения формы.

Согласно данной теории прочности опасное состояние материала при сложном напряженном состоянии наступает тогда, когда удельная потенциальная энергия изменения формы достигает величины, соответствующей пределу текучести при простом растяжении.

В частном случае, когда σ_y =  0, то, приняв σ_x = σ и τ_xy = τ, найдем



Рассмотренная теория хорошо согласуется с экспериментами для пластичных материалов и широко применяется на практике.

Теория прочности Мора (V теория прочности)

Теория прочности Мора позволяет учесть различие в свойствах материалов при растяжении и сжатии. Ее можно получить путем модификации теории наибольших касательных напряжений в соответствии с уравнением:

для пластичных материалов, или



для хрупких материалов.

Условие прочности по теории Мора имеет следующий вид:



 

Замечания о выборе теории прочности

Обзор многочисленных теорий предельных состояний показывает, что совершенных теорий еще нет. Каждая из существующих теорий справедлива только в определенных условиях и для определенных материалов. Рассмотренными выше теориями можно пользоваться только при напряженных состояниях с главными напряжениями разных знаков. Возможность применения этих теорий в случаях трехосного растяжения или сжатия требует дополнительной экспериментальной проверки.

При выборе теории прочности в случае плоского напряженного состояния и объемного напряженного состояния с главными напряжениями разных знаков надо учитывать свойства материала. Если материал пластичен и одинаково работает на растяжение и сжатие, то следует пользоваться теорией наибольшей энергии формоизменения  или теорией максимальных касательных напряжений. Если пластичный материал неодинаково сопротивляется растяжению и сжатию, то следует применить теорию Мора. Расчет хрупких материалов при указанных напряженных состояниях следует производить по теории Мора.

Совместные действия изгиба и кручения стержня
В случае изгиба с кручением от крутящего момента в поперечных сечениях бруса возникают касательные напряжения, которые рассчитываются по разному для круглых и прямоугольных брусьев. Вследствие этого, рассматривать расчет сечений произвольной формы не представляется возможным.

Кручение с изгибом – частный случай сложного сопротивления, который может рассматриваться как сочетание чистого кручения и поперечного изгиба.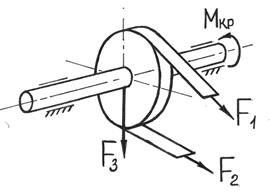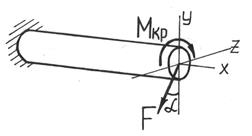




Рис.7.9

 

Определение внутренних усилий и напряжений при кручении с изгибом
Для определения внутренних усилий воспользуемся методом сечений:













 Обычно две составляющие поперечной силы (Q_y, Q_z) и изгибающего момента (M_y, M_z) приводят к их полным результирующим




Расчет валов круглого (кольцевого) поперечного сечения на кручение с изгибом
Исследуем этот вид деформации стержня на примере расчета вала кругового (кольцевого) поперечного сечения на совместное действие изгиба и кручения.

У кругового и кольцевого поперечного сечений все центральные оси главные, поэтому косого изгиба у вала вообще не может быть, следовательно, нет смысла в каждом сечении иметь два изгибающих момента M_x, и M_y, а целесообразно их заменить результирующим (суммарным) изгибающим моментом (рис.7.9)



Опасное сечение при кручении с изгибом устанавливается из совместного анализа эпюр крутящего M_x и полного изгибающего M_и моментов. Если в сечении вала постоянного диаметра с наибольшим изгибающим моментом М действует наибольший крутящий момент М_кр, то это сечение является опасным.

Наибольшие напряжения изгиба возникают в точках  наиболее удаленных от нейтральной оси



где W_изг — момент сопротивления при изгибе.
В этих же точках имеют место и наибольшие касательные напряжения кручения



где W_р — момент сопротивления при кручении.

Условие прочности по III гипотезе записывается в виде



или



где    - эквивалентный момент по третьей гипотезе прочности.

Условие прочности по IV гипотезе прочности записывается в виде



или



где    - эквивалентный момент по четвертой гипотезе прочности.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

- Что такое сложное сопротивление стержней?

- Какие виды деформации бруса называют сложным со­противлением?

- Сформулируйте принципы,  на  которых строится  рас­чет брусьев при сложном сопротивлении?

- В чем заключается принцип независимости действия сил?

- Опишите методику определения компонентов внутренних сил при сложном сопротивлении?            

- Какой изгиб называется косым?

- Какие точки сечения будут опасными при косом изгибе?

- Как записывают условия прочности при косом изгибе для балки из пластичного материала?

- По каким формулам определяются нормальные напряжения в поперечных сечениях балки при косом изгибе?

- Какой вид сложного сопротивления называется внецентренным растяжением (или сжатием)?

- К каким равнодействующим приводятся внутренние силы при внецентренном растяжении (или сжатии)?

- Какие виды напряжений испытывает сжимаемый стержень при внецентренном приложении сжимаемой или растягиваемой нагрузки?

- По каким формулам определяются нормальные напряжения в поперечных сечениях стержня при внецентренном растяжении и сжатии? Какой вид имеет эпюра этих напряжений?

- Как определить положение наиболее напряженной (опасной) точки сечения бруса при внецентренном растяжении (сжатии)?

- Как составить условие прочности бруса при внецентренном растяжении (сжатии)?

- Какие напряжения возникают в поперечном сечении бруса при изгибе с кручением?

- Как находятся опасные сечения бруса круглого сечения при изгибе с кручением?

- Как выполняют проверку безопасной прочности при кручении с изгибом круглого бруса?

- Что представляет собой эквивалентное напряжение?

- Чем отличаются между собой различные теории прочности?

- Какое назначение имеют гипотезы предельных напряжений состояний (гипотезы прочности)?

- В чем заключается сущность гипотезы прочности максимальных касательных напряжений и энергетической гипотезы прочности?

- Как формулируется теория прочности удельной потенциальной энергии,  идущей  на  изменение формы  и  условие прочности по ней?

- В чем состоит теория прочности Мора?

- В чем преимущество гипотезы прочности Мора?