24.05.05 Прикладная механика.. Учебное пособие по дисциплине Механика Модуль Прикладная механика
 Скачать 1.89 Mb. Скачать 1.89 Mb.
|
Условие прочности при кручении вала круглого и кольцевого сеченияУсловие прочности при кручении с учетом принятых обозначений формулируется следующим образом: максимальные касательные напряжения, возникающие в опасном сечении вала, не должны превышать допускаемых напряжений и записывается в виде где - берется либо на основании опытных данных, либо (при отсутствии нужных опытных характеристик) по теориям прочности, соответствующим материалу. Рациональная форма сечения вала Анализируя эпюру касательных напряжений (рис.5.6) можно отметить, что наибольшие напряжения возникают на поверхности вала, в центральной части они значительно меньше и на продольной оси равны нулю. Следовательно, в сплошном валу материал, находящийся в центральной части в значительной степени недогружен, его вклад в прочность вала мал. Поэтому рациональным для валов считается кольцевое сечение. 5.2. Деформации при кручении и условие жесткости вала Из выражения (5.5) следует, что интегрируя которое по длине вала, получим: Если Мк = const и по всей длине вала, то абсолютный угол закручивания где - жесткость вала при кручении. При скачкообразном изменении по длине бруса крутящего момента угол закручивания между его начальным и конечным сечениями определяется как сумма углов закручивания по участкам с постоянным Mk Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания Для обеспечения требуемой жесткости вала необходимо, чтобы наибольший относительный угол закручивания не превосходил допускаемого: Эта формула выражает условие жесткости вала при кручении. Обычно принимается на 1 м длины вала. 5. 3. Расчеты на прочность и жесткость валов круглого и кольцевого сечений При расчетах на прочность при кручении (также как и при растяжении) могут решаться три задачи: а) проверочный расчет – проверить, выдержит ли вал приложенную нагрузку; б) проектировочный расчет - определить размеры вала из условия его прочности; в) расчет по несущей способности - определить максимально допустимый крутящий момент. - При проверочном расчете на прочность рекомендуется следующий порядок расчета валов при кручении: 1) по схеме вала и действующим на него скручивающим моментам строят эпюру внутренних крутящих моментов по отдельным участкам; 2) выбирают материал для рассчитываемого вала и определяют для этого материала допускаемое напряжение, например по формуле (5.9), ; 3) для участка вала с максимальным по модулю значением крутящего момента записывают условие прочности при кручении - Проектировочный расчет проводится, исходя из условия прочности на основе следующего соотношения: Для сплошного круглого сечения Для кольцевого сечения Определив размеры вала из условия прочности, проверяют вал на жесткость. Условие жесткости требует, чтобы максимальный относительный угол закручивания , был меньше или в предельном случае равен допускаемому углу закручивания единицы длины вала, т.е. Расчет заклепок на срез На практике целый ряд деталей и элементов конструкций работает в таких условиях, что внешние силы стремятся их разрушить именно путем сдвига. В соответствии с этим при проверке прочности таких элементов на первый план выступают касательные напряжения. Простейшими примерами подобных деталей являются болтовые и заклепочные соединения. Для образования заклепочного соединения в обоих листах просверливают или продавливают отверстия. В них закладывается нагретый до красного каления стержень заклепки с одной головкой; другой конец заклепки расклепывается ударами специального молотка или давлением гидравлического пресса (клепальной машины) для образования второй головки. Мелкие заклепки (малого диаметра — меньше 8 мм) ставятся в холодном состоянии (авиационные конструкции). Для изучения работы заклепок рассмотрим простейший пример заклепочного соединения (рис.5.7). Шесть заклепок, расположенных в два ряда, соединяют два листа внахлестку. Под действием сил Р эти листы стремятся сдвинуться один по другому, чему препятствуют заклепки, на которые и будет передаваться действие сил P). 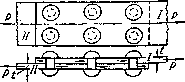 Рис.5.7 Для проверки прочности заклепок применим общий порядок решения задач сопротивления материалов. На каждую заклепку передаются по две равные и прямо противоположные силы: одна—от первого листа, другая — от второго. Опытные исследования показывают, что одни из заклепок ряда нагружаются больше, другие — меньше. Однако к моменту разрушения усилия, передающиеся на различные заклепки, более или менее выравниваются за счет пластических деформаций. Поэтому принято считать, что все заклепки работают одинаково. Таким образом, при n заклепках в соединении, изображенном на рис.5.7, на каждую из них действуют по две равные и противоположные силы (рис.5.8); эти силы передаются на заклепку путем нажима соответствующего листа на боковую полуцилиндрическую поверхность стержня. Силы стремятся перерезать заклепку по плоскости mk раздела обоих листов. 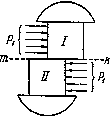 Рис.5.8 Для вычисления напряжений, действующих по этой плоскости, разделим мысленно заклепочный стержень сечением mk и отбросим нижнюю часть (рис.5.8). Внутренние усилия, передающиеся по этому сечению от нижней части на верхнюю, будут уравновешивать силу т. е. будут действовать параллельно ей в плоскости сечения, и в сумме дадут равнодействующую, равную . Следовательно, напряжения, возникающие в этом сечении и действующие касательно к плоскости сечения, это — касательные напряжения . Обычно принимают равномерное распределение этих напряжений по сечению. Тогда при диаметре заклепки d на единицу площади сечения будет приходиться напряжение: Величина допускаемого касательного напряжения , или, как говорят, допускаемого напряжения на срез, принято определять в виде: т. е. действительное касательное напряжение в материале заклепки должно быть равно допускаемому , или меньше его. Из этого условия можно определить необходимый диаметр заклепок, если задаться их числом, и наоборот. Обычно задаются диаметром заклепочных стержней d в соответствии с толщиной t склепываемых частей (обычно ) и определяют необходимое число заклепок n: 5.4. Расчет заклепок на смятие и листов на разрыв Помимо среза заклепкам и соединяемым листам в конструкции угрожают и иные опасности. Так как передача сил на заклепочный стержень происходит путем нажатия стенок заклепочного отверстия на заклепку, то необходимо установить, не произойдет ли наружное обмятие этого стержня или стенок отверстия, — произвести проверку на смятие. Под смятием понимают пластическую деформацию, возникающую в соединениях на поверхностях контакта. Возникающие при этом напряжения являются нормальными, закон распределения которых по поверхности контакта достаточно сложен. На рис.5.9 указана примерная схема передачи давлений на стержень заклепки. Закон распределения этих давлений по цилиндрической поверхности нам неизвестен; он во многом зависит от неправильностей формы заклепочного отверстиями стержня, вызванных условиями изготовления конструкции. Поэтому расчет производится условно. Принято считать, что неравномерное давление, передающееся на поверхность заклепки от листа, распределяется равномерно по диаметральной плоскости сечения заклепки. При этом напряжение по этой диаметральной плоскости оказывается примерно равным наибольшему сминающему напряжению в точке А поверхности заклепки. 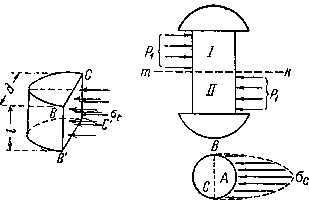 Рис.5.9 Чтобы вычислить это условное напряжение смятия, необходимо разделить силу, приходящуюся на заклепку, на площадь диаметрального сечения ВСС'В'. Эта площадь представляет собой прямоугольник, одной стороной которого служит диаметр заклепки, другая же равна толщине листа, передающего давление на стержень заклепки. Так как давление на одну заклепку равно P/n, то условие прочности на смятие будет иметь вид: где — допускаемое напряжение на смятие. Отсюда необходимое число заклепок ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ - Какой вид нагружения называется кручением? - При каком нагружении возникает кручение бруса (вала)? - Какой силовой фактор вызывает закручивание бруса? - Что такое крутящий момент? - Что называется валом? - Когда в брусе возникают деформации кручения? - Как определяют величину крутящего момента, действующего в сечении? - Какое правило знаков для Т принято при построении эпюр? - Как строятся эпюры крутящих моментов? - Как определяют угол закручивания на участке вала? - Что называют относительным углом закручивания θ (или кривизной кручения kt)? - Какие напряжения возникают в поперечном сечении круглого вала при кручении и как они направлены? - Какое напряженное состояние возникает в каждой точке вала круглого сечения при кручении? - Что называется жесткостью сечения при кручении? - Что выражает условие жесткости при кручении? - Чем объясняется, что вал кольцевого сечения при кручении экономичнее вала сплошного сечения? - Как выполняют расчет вала на прочность? - Как называется напряженное состояние, возникающее при кручении круглого бруса (вала)? - Какие деформации возникают при кручении? - Какие гипотезы выполняются при деформации кручения? - По какой формуле определяется касательное напряжение при кручении? - Как распределяется касательное напряжение при кручении? Чему равно напряжение в центре круглого поперечного сечения? - Как вычислить потенциальную энергию деформации, накапливаемую валом при кручении? - В каких точках бруса круглого сечения возникают наибольшее касательное напряжение? Как их вычисляют? - Как определяется диаметр вала из условия жесткости? - Как выбираются допускаемые напряжения при расчете на кручение? - Укажите единицы измерения напряжений сдвига и смятия и модуля упругости. - Что такое срез? - Что такое смятие? - Какие допущения проложены в основу практических расчетов элементов конструкции на срез и смятие? - Опишите процесс разрушения при срезе? - Как выбирается допускаемое напряжение при сдвиге? - Что понимается под деформацией смятия? - В чем заключается явление смятия и в каких местах оно наблюдается? - Как записывается условие прочности на срез и на смятие? - Как находится площадь смятия при соприкосновении цилиндрических поверхностей? - Как определяется расчетная величина площади на срез и на смятие при болтовых соединениях листовых элементов внахлестку и с помощью накладок? - Какие виды деформации испытывает нагруженное заклепочное соединение? - Как учесть количество деталей, использованных для передачи нагрузки при расчетах на сдвиг и смятие? - Как определить необходимое количество заклёпок, обеспечивающее безопасную прочность соединения? 6. Прямой изгиб |
