24.05.05 Прикладная механика.. Учебное пособие по дисциплине Механика Модуль Прикладная механика

• Название: Учебное пособие по дисциплине Механика Модуль Прикладная механика
• Дата: 17.04.2023
• Размер: 1.89 Mb.
• Имя файла: 24.05.05 Прикладная механика..docx
• Тип: Учебное пособие; #1068488
• страница: 12 из 18

Общие сведения

Изгибом называется вид нагружения бруса, при котором к нему прикладывается поперечная нагрузка, лежащая в плоскости проходящей через продольную ось (рис.6.1, а). В этой же плоскости располагается изогнутая ось стержня (упругая линия) (рис.6.1, б). Брус, работающий при изгибе, называется балкой. Изгиб называется плоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения (рис.6.1).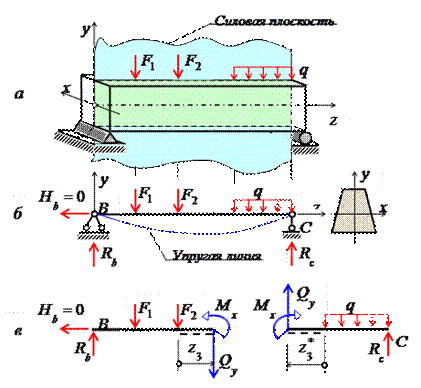



Рис. 6.1

При плоском поперечном изгибе в балке возникают два вида внутренних усилий (рис.6.1,в): поперечная сила Q_y , где y – ось симметрии (главная центральная ось) и изгибающий момент M_x. , гдеx – другая главная центральная ось сечения, нормальная к оси симметрии. В раме при плоском поперечном изгибе возникают три усилия: продольная N,  поперечная Q силы и изгибающий момент M.

Если изгибающий момент M_x является единственным внутренним силовым фактором, то такой изгиб называется чистым (рис.6.2). При наличии поперечной силы Q_y изгиб называется поперечным. Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; попереч­ный изгиб относят к простым видам сопротивления условно, так как в большинстве слу­чаев (для достаточно длинных балок) действием поперечной силы при расчетах на проч­ность можно пренебречь.

Косой изгиб - изгиб, при котором нагрузки действуют в одной плоскости, не совпадающей с главными плоскостями инерции.

6.1. Построение эпюр поперечной силы и изгибающего момента
Для того, чтобы произвести расчет балки на изгиб, необходимо знать величину наибольшего изгибающего момента М и положение сечения, в котором он возникает. Точно также, надо знать и наибольшую поперечную силу Q. Для этой цели строят эпюры изгибающих моментов и поперечных сил. По эпюрам легко судить о том, где будет максимальное значение момента или поперечной силы.

Эпюра внутренней силы – график, показывающий изменение этой силы по длине балки.

Для построения эпюр балка разбивается на участки, в пределах которых функция внутренней силы не меняет своего аналитического выражения. За границы участков принимаются сечения, в которых приложены внешние нагрузки: сосредоточенные силы, сосредоточенные моменты, начинается или заканчивается распределенная нагрузка одного направления и изменяющаяся по одному закону, а также начало и конец балки.

Перед тем, как определять внутренние усилия (поперечные силы и изгибающие моменты) и строить эпюры, как правило, надо найти опорные реакции, возникающие в закреплении стержня. Если опорные реакции и внутренние усилия можно найти из уравнений статики, то конструкция называется статически определимой. Чаще всего мы встречаемся с тремя видами опорных закреплений стержней: жестким защемлением (заделкой), шарнирно-неподвижной опорой и шарнирно-подвижной опорой. На рис. 6.2 показаны эти закрепления. Для неподвижной (рис 6.2,б) и подвижной (рис. 6.5,в) опор приведены два эквивалентных обозначения этих закреплений. Напомним, что при действии нагрузки в одной плоскости в заделке возникают три опорных реакции (вертикальная, горизонтальная реакции и сосредоточенный реактивный момент) (рис. 6.2,а); в шарнирно-неподвижной опоре – две реактивные силы (рис. 6.2,б); в шарнирно-подвижной опоре – одна реакция – сила, перпендикулярная плоскости опирания (рис.6.2,в).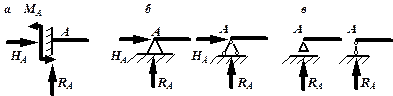

Рис. 6.2. Опорные реакции: а – в заделке; б – в шарнирно-неподвижной опоре;

в – в шарнирно-подвижной опоре
После определения опорных реакций внутренние усилия в статически определимых конструкциях определяем с помощью метода сечений.

Как было сказано выше, при плоском поперечном изгибе в балке возникают два внутренних усилия: поперечная сила Q и изгибающий момент M. В соответствии с методом сечений поперечную силуможно найти как сумму проекций всех внешних сил, взятых с одной стороны от сечения, на ось, перпендикулярную оси стержня (ось z). Изгибающий момент равен сумме моментов всех внешних сил, взятых с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения (оси y).

Для того чтобы можно было вести расчет с любого конца балки, необходимо принять правило знаков для внутренних силовых факторов.

Если внешняя сила вращает отрезанную часть балки по часовой стрелке, то сила является положительной, если внешняя сила вращает отрезанную часть балки против хода часовой стрелки, то сила является отрицательной.

Если под действием внешней силы изогнутая ось балки принимает вид вогнутой чаши, такой, что идущий сверху дождь будет наполнять ее водой, то изгибающий момент является положительным. Если под действием внешней силы изогнутая ось балки принимает вид выпуклой чаши, такой, что идущий сверху дождь не будет наполнять ее водой, то изгибающий момент является отрицательным.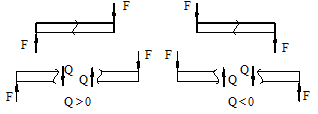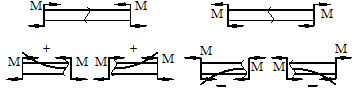


а)                                         б)
Рис.6.3. а - правило знаков для поперечной силы Q; б - правило знаков для изгибающего момента M.

 

Достаточно очевидно и подтверждается опытом, что балка при изгибе деформируется таким образом, что волокна, расположенные в выпуклой части, растягиваются, а в вогнутой – сжимаются. Между ними лежит слой волокон, который лишь искривляется, не изменяя своей первоначальной длины (рис.6.4). Этот слой называется нейтральным или нулевым, а его след на плоскости поперечного сечения – нейтральной (нулевой) линией или осью.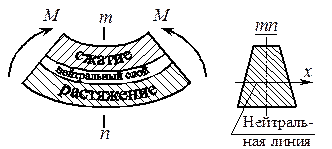



Рис.6.4
При построении эпюр Q и М договоримся на эпюре Q положительные значения откладывать сверху нулевой линии. На эпюре М у строителей принято откладывать положительные ординаты снизу. Такое правило построения эпюры М называется построением эпюры со стороны растянутых волокон, т. е. положительные значения М откладываются в сторону выпуклости изогнутой балки.

Рассмотрим для простоты балку с прямоугольным поперечным сечением (рис.6.9). Следуя методу сечений, мысленно проведем разрез и отбросим какую-либо часть балки, а другую оставим. На оставшейся части покажем действующие на нее силы и в поперечном сечении – внутренние силовые факторы, которые являются результатом приведения к центру сечения сил, действующих на отброшенную часть. Учитывая, что внешние силы и распределенные нагрузки лежат в одной плоскости и действуют перпендикулярно оси балки, в сечении получим поперечную силу Q_y и изгибающий момент M_x. Эти внутренние силовые факторы заранее неизвестны, поэтому их показывают в положительном направлении в соответствии с принятыми правилами знаков.

На рис.6.5 показаны два случая оставшейся части: левая и правая.

Для определения величины Q_y и M_x составляются два уравнения равновесия для оставшейся части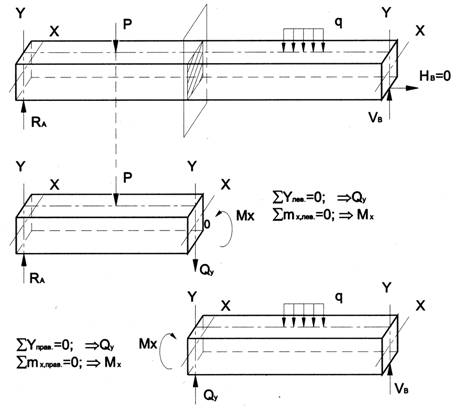







Рис.6.5
Изгибающий момент M_x, действующий в поперечном сечении балки, по величине равен сумме моментов всех внешних сил, приложенных к рассматриваемой отсеченной части бруса, относительно центральной оси x этого сечения:



Если внешняя сила в данном сечении растягивает нижние волокна балки, то момент этой силы в этом сечении считается положительным, если растягиваются верхние волокна балки, то момент этой силы будет отрицательным.

Поперечная сила Q_y в сечении бруса, по величине равна сумме проекций всех внешних сил, действующих на отсеченную часть бруса, на ось перпендикулярную оси бруса (ось y):



Уравнение момента составляется относительно оси Х, проходящей в поперечном сечении через точку на оси балки – тогда поперечная сила в уравнение не входит и величина M_x определяется независимо от Q_y. Можно доказать, что результат вычислений  Q_y и M_x не зависит от того, равновесие какой оставшейся части рассматривается.

Рассмотрим характерный пример (рис. 6.6,а) и установим не­обходимые правила. Решение задачи, как правило, начинается с определения полной системы внешних сил. Для этого отбросим опоры и заменим их соответствующими реакциями (рис. 6.6,б), выполняющими ту же роль, что и опорные закрепления.

Заданная система статически определима, следовательно, из ус­ловий равновесия системы, т.е. равенства нулю суммы моментов всех сил относительно шарнирных опор (в шарнирах нет ограниче­ний поворота сечений балки, поэтому изгибающих моментов не возникает)   и  , определяем вертикальные реакции в опорах:



Для определения   имеем:  откуда  . Для проверки правильности вычислений воспользуемся усло­вием равенства нулю суммы всех вертикальных сил   откуда получим



0 = 0.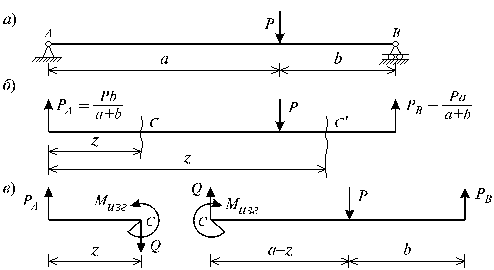



Рис. 6.6

               

Для определения внутренних силовых факторов  изгибающего момента М(z) и поперечной силы Q(z) как функций от продоль­ной координаты z, воспользуемся методом сечений. Для полу­чения этих зависимостей балку разбивают на участки, границами которых являются следующие точки: начало и конец балки; точки приложения сосредоточенных усилий; начало и конец действия распределенных усилий; сечения, в которых скачкообразно изменя­ется жесткость балки; в точках, где происходит изменение ориен­тации элементов, если имеем дело с стержневой системой со сложной структурой.

Заданная система состоит из двух участков  первого (0≤z≤a) и второго (a≤z≤a+b). Следовательно, задавая последовательно сечения, принадлежащие к первому и второму участкам, и рассмат­ривая равновесие отсеченных частей системы при действии на них всех внешних сил и внутренних уси­лий, определим выражения для внутренних сило­вых факторов.

Из условия равновесия   отсеченной части системы, расположенной левее от сечения z₁ (первый участок), (см. рис. 6.6, в), получим:



Для определения Q_y и M_x на втором участке рассмотрим рав­новесие отсеченной части балки, расположенной правее от сечения z₂ (см. рис. 6.10, б), т.е.   откуда и определим:



Эпюры Q_y и M_x изображены на рис. 6.7. Заметим, что эпюры изгибающих моментов M_x, как и поперечных сил Q_y строятся на оси бруса, однако в отличие от эпюры поперечных сил знак момента не указывается, а ординаты изгибающего момента откла­дываются co стороны растянутых волокон.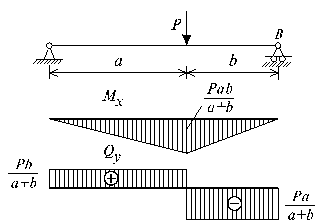


Рис. 6.7

 

6.2. Основные дифференциальные соотношения теории изгиба
Пусть брус нагружен произвольным образом распределенной нагрузкой q=f(z) (рис. 6.8,а).



Рис. 6.8

               

Выделим из бруса элемент длинойdz и приложим по его краям положительные внутренние усилия (рис. 6.8,б). В пределах малого отрезкаdz нагрузку q можно считать распределенной равномерно. Приравняем нулю сумму проекций всех сил на вертикальную ось y и сумму моментов всех сил относительно поперечной оси x, прохо­дящей через точку С (рис. 6.8,б), получим:





Производя упрощения и отбрасывая величины высшего поряд­ка малости, получим теорему Журавского (теорему Шведлера):



откуда



Указанные дифференциальные зависимости при изгибе позволяют установить некоторые особенности эпюр поперечных сил и изгибающих моментов.

1. Эпюра Q является прямолинейной на всех участках. На тех участках, где нет распределенной нагрузки, эпюра Q ограничена прямыми, параллельными оси эпюры, а эпюра М, в общем случае, – наклонными прямыми (рис. 6.9).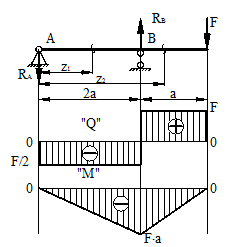



Рис.6.9

 

2. На тех участках, где к балке приложена равномерно распределенная нагрузка, эпюра Q ограничена наклонными прямыми, а эпюра М – квадратичными параболами (рис. 6.14). При построении эпюры М на сжатых волокнах, выпуклость параболы обращена в сторону, противоположную действию распределенной нагрузки (рис. 6.10,а, б).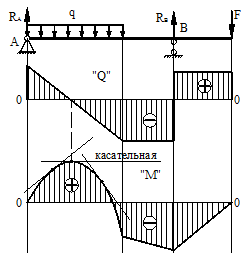



Рис.6.10

3. В тех сечениях, где Q = 0, касательная к эпюре М параллельна оси эпюры (рис. 6.10, 6.11). Изгибающий момент в таких сечениях балки экстремален по величине (М_max, M_min).

4. На участках, где Q>0, M возрастает, то есть слева на право положительные ординаты эпюры M монотонно увеличиваются, отрицательные – монотонно уменьшаются (рис. 6.9, 6.10); на тех участках, где Q < 0, M убывает (рис. 6.13, 6.14).

5. В тех сечениях, где к балке приложены сосредоточенные силы:

а) на эпюреQ будут скачки на величину и в направлении приложенных сил (рис. 6.13, 6.14).

б) на эпюре M будут переломы (рис. 6.9, 6.10), острие перелома направлено против действия силы.

6. В тех, сечениях, где к балке приложены сосредоточенные моменты, на эпюре M будут скачки на величину этих моментов, на эпюреQ никаких изменений не будет (рис. 6.12).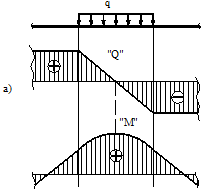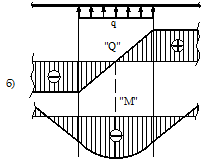



Рис.6.11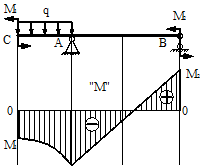

 



Рис.6.12

 

7. Если на конце консоли или в концевой опоре приложен сосредоточенный момент, то в этом сечении изгибающий момент равен внешнему моменту (сеченияC и B на рис. 6.12).

8. ЭпюраQ представляет собой диаграмму производной от эпюры M. Значит, ординаты Q пропорциональны тангенсу угла наклона касательной к эпюре M (рис. 6.14).

9. Порядок линии на эпюре Q  всегда на единицу меньше, чем на эпюре M. Например, если эпюра M  - квадратная парабола, то эпюра Q  на этом участке - наклонная прямая; если эпюра M - наклонная прямая, то эпюра Q  на этом участке - прямая, параллельная оси; если M =const (прямая, параллельная оси), то на этом участке Q=0.

10. Приращение функции изгибающего момента на рассматриваемом участке численно равно площади эпюры поперечных сил на этом участке с соответствующим знаком. При построении эпюры  для изгибающего момента слева направо знаки приращения функции изгибающего момента и площади эпюры поперечных сил совпадают. При построении эпюры изгибающих моментов справа налево знаки приращения функции изгибающих моментов и площади эпюры поперечных сил противоположны. 

6.3. Напряжение при чистом изгибе
Рассмотрим наиболее простой случай изгиба, называемый чистым изгибом и выведем  формулу для определения нормальных напряжений для данного случая. Отметим, что методами теории упругости можно получить точную зависимость для нормальных напряжений при чистом изгибе, если же решать эту задачу методами сопротивления материалов, необходимо ввести некоторые гипотезы.

Таких гипотез при изгибе три:

1) гипотеза плоских сечений (гипотеза Бернулли). Сечения плоские до деформации остаются плоскими и после деформации, а лишь поворачиваются относительно некоторой линии, которая называется нейтральной   осью сечения балки. При этом волокна балки, лежащие с одной стороны от нейтральной оси будут растягиваться, а с другой - сжиматься; волокна, лежащие на нейтральной оси своей длины не изменяют;

2) гипотеза о постоянстве нормальных напряжений - напряжения, действующие на одинаковом расстоянии у от нейтральной оси, постоянны по ширине бруса;

3) гипотеза об отсутствии боковых давлений - соседние продольные волокна не давят друг на друга.

Кроме этих гипотез следует ввести ряд ограничений:

1. Балка имеет хотя бы одну плоскость симметрии, и все внешние силы лежат в этой плоскости.

2. Материал балки подчиняется закону Гука, причем модуль упругости при растяжении и сжатии одинаков.

3. Соотношения между размерами балки таковы, что она работает в условиях плоского изгиба без коробления или скручивания.

Как было отмечено выше, под чистым изгибом понимается такой вид сопротивления, при котором в поперечных сечениях бруса возникают только изгибающие моменты, а попе­речные силы равны нулю. Для тех участков бруса, где соблюдается данное условие, изгибающий момент, вдоль продольной оси z принимает постоянное значение. Так как в любом сечении стержня при чистом изгибе M_x(z)=const, то для однородного бруса постоянного поперечного сечения изменение кривизны постоянно вдоль оси z. Под действием изгибающих мо­ментов ось бруса искривляется. Исходя из этого, ось бруса прини­мает форму дуги окружности с радиусом кривизны   (рис. 6.13). В данном случае с высокой степенью точности справедлива гипотеза плоских сечений. Следовательно, точки, расположенные до изгиба в плоскости поперечного сечения бруса, в результате изгиба пере­местятся в пространстве таким образом, что их совокупность снова образует плоскость.

Процесс формирования деформаций при чистом изгибе может рассматриваться как результат поворота плоских поперечных сече­ний друг относительно друга.

Рассмотрим два смежных сечения, отстоящих один от другого на расстоянии  dz  (рис. 6.13).

В результате изгиба эти сечения наклонятся, образуя между со­бой угол dθ, в связи с чем верхние волокна удлиняются, а ниж­ние  укоротятся. Очевидно, что при этом существует слой, длина которого не изменилась. Назовем его нейтральным слоем и обозначим отрезком СD. При этом  . Произвольный отрезок АВ, расположен­ный от СD на расстоянии y, в результате изгиба удлинится на величину  . С учетом построений, изображенных на рис. 6.26, легко определить величину его относительной линейной деформации:



 

Рис. 6.13

 

Если предположить, что продольные волокна не давят друг на друга, то каждое из них будет находиться в условиях простого растяжения  сжатия. Тогда переход от деформаций к нормальным напряжениям   можно осуществить посредством закона Гука: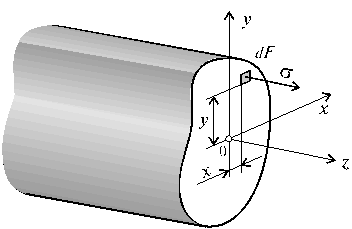



 


Рис. 6.14

               

Устано­вим положение нейт­ральной оси x, от кото­рой происходит отсчет координаты у (рис.6.14). Учитывая, что сумма элементарных сил   по площади попе­речного сечения A дает нормальную силу N_z. Но при чистом изгибе N_z =0, следовательно:



Как известно, последний интеграл представляет собой статиче­ский момент сечения относительно нейтральной линии (оси x). Статический момент равен нулю, значит, нейтральная линия про­ходит через центр тяжести сечения.

Выразим момент внутренних сил относительно нейтральной оси M_x  через σ. Очевидно, что



C учетом выражения (2) получим:



Откуда



где    кривизна нейтрального волокна; EI_x  жесткость бруса.

Из формулы (3), исключая  , окончательно получим:



Эта формула была впервые получена Ш. Кулоном в 1773 году.

Таким образом, нормальные напряжения в любой точке сечения прямо пропорциональны величине изгибающего момента и расстоянию точки от нейтральной линии сечения и обратно пропорционально моменту инерции сечения относительно нейтральной оси.

Из выражения (5) можно сделать ряд важных выводов:

1) центр тяжести сечения балки является началом координат для анализа напряжений и приведения внешних сил;

2) напряжения изгиба зависят от значений изгибающего момента, момента инерции сечения и координаты точки, в которой это напряжение определяется;

3) напряжения в любой точке, лежащей на одинаковом расстоянии от нейтральной линии, равны между собой;

4) нормальные напряжения не зависят, а упругие перемещения зависят от модуля упругости материала балки.

В нейтральном слое при y=0 напряжения σ=0, в сжатой зоне (при y<0, рис.6.26) напряжения становятся отрицательными, в растянутой зоне (при y>0, рис. 6.26) напряжения становятся положительными. По мере удаления от нейтрального слоя нормальные напряжения σ в поперечном сече­нии бруса при его изгибе изменяются по линейному закону в зависимости от координаты y и принимают максимальное значение на уровне крайних волокон (при  ):





Измеряется осевой момент сопротивления единицами длины в третьей степени, например (см³). Физический смысл момента сопротивления состоит в следующем: чем больше W_x, тем больший изгибающий момент может принять на себя балка, не подвергаясь опасности разрушения. Таким образом, величина момента сопротивления характеризует влияние формы и размеров поперечного сечения балки на ее способность сопротивляться внешним нагрузкам, не разрушаясь.

При симметричном относительно нейтральной линии сечении, например, прямоугольном, расстояния до крайних растянутых и сжатых волокон одинаковы и такое сечение имеет одно вполне определенное значение момента сопротивления относительно оси Oz. Так, при высоте прямоугольника (рис. 6.15, а), равной h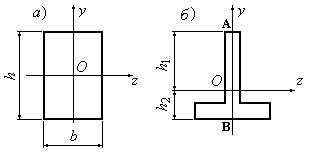





Рис. 6.15

 

Если сечение несимметрично относительно нейтральной линии – тавр, мы получим два момента сопротивления: один для волокон А (рис. 6.15,б):   и другой для волокон В:  . Теперь в формулу (6) следует вводить: W₁   при вычислении напряжений в точке А и W₂   при вычислении напряжений в точке В.

Для круга



Для прокатных профилей (двутавра, швеллера, уголка) M_x  приводится в таблицах сортамента.

Формулой (6) удобно пользоваться для расчета балок пластичного материала в упругой области, одинаково работающего на растяжение и сжатие. Поскольку знак напряжения в этом случае не имеет значения, напряжения вычисляются по модулю, и условие прочности при изгибе балки в форме призматического стержня получает вид



где maxM_x — максимальное значение изгибающего момента (легко определяемое по его эпюре), [σ] - допускаемое напряжение на простое растяжение (сжатие). Напомним, что чистый изгиб балки сводится к растяжению и сжатию ее волокон (неравномерному в отличие от деформации растяжения (сжатия) призматического стержня, при котором σ=const).
При расчете балок из хрупких материалов следует различать наибольшие растягивающие maxσ_pи наибольшие сжимающие maxσ_c напряжения, которые также определяются по модулю непосредственно и сравниваются с допускаемыми напряжениями на растяжение [σ_p] и сжатие [σ_c]. Условие прочности в этом случае будет иметь вид:





В зависимости от того, чему лучше сопротивляется материал, приходится  соответсвующим образом конструировать сечение, выбирая его форму и размеры так, чтобы удовлетворяли условию прочности.

Из условия (7) формулируют три рода задач на прочность при изгибе:

1. Проверка прочности: задана балка, нагрузка, известен материал. Строится эпюра M_x  – определяется M_max, вычисляется W_x и по (7) проверяется условие прочности.

2. Определение максимально допустимой нагрузки по условию прочности.



Заданы размеры балки, характер нагрузки, материал балки.

Строится эпюра M_x  – определяется M_max от параметра нагрузки, вычисляется W_x и по (8) находят наибольший параметр нагрузки.

3. Конструирование балки – определение размеров ее поперечного сечения.



Строится эпюра   – определяется  , вычисляется правая часть (9) и подбираются размеры поперечного сечения, удовлетворяющие (9).

Для прямоугольного сечения 



Обычно задаются отношением



Тогда



отсюда 


Задаваясь шириной b по (10) получимh.

Для двутаврового сечения по таблице сортамента подбирают номер  двутавра  с  W_x  большим, чем правая часть (9).
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
- Что называется балкой?

- Какой вид нагружения называется изгибом?

- Какой изгиб называется чистым, поперечным?

- Какой изгиб называют чистым, поперечным, прямым и косым?

- Чем отличается чистый изгиб от поперечного изгиба, прямой изгиб от косого изгиба?

- Сформулируйте определение «поперечный изгиб»?

- Сформулируйте понятие «чистый изгиб»?

- Что понимается под волокнами бруса? В чем сущность гипотезы   плоских   сечений  и  допущения о ненадавливании волокон друг на друга?

- Что такое нейтральная линия, силовая линия?

- Какие внутренние усилия возникают в поперечных сечениях балки в общем случае действия на неё плоской системы сил?

- Как формулируется гипотеза плоских сечений?

- Что представляет собой нейтральный слой и нейтральная ось?

- Какие силовые факторы возникают в сечении балки при чистом изгибе?

- Какие силовые факторы возникают в сечении при поперечном изгибе?

- Что такое поперечная сила (Q_y)?   Как определяется Q_y  через внешние силы?

- Какие виды опор встречаются при расчете балок? Чем они отличаются?

- Какое правило законов для определения поперечной силы используется?

- Каково правило законов для определения изгибающего момента используется?

- Как вычисляется изгибающий момент в поперечном сечении балки?

- Как вычисляются поперечная и продольная силы в поперечном сечении балки?

- Как определить значение поперечной силы и изгибающего момента в произвольном сечении балки?

- Как определить знаки поперечной силы и изгибающего момента?

- Как проверить правильность определения опорных реакций?

- Как формулируется гипотеза плоских сечений?

- По какой формуле определяются нормальные напряжения в поперечном сечении балки при чистом изгибе и как они изменяются по высоте балки?

- Для чего строят эпюры внутренних силовых факторов?

- Какая нагрузка вызывает скачок на эпюре поперечной силы?

- Какая нагрузка вызывает скачок на эпюре изгибающего момента?

- Как находят опасные сечения?

- Какая дифференциальная зависимость связывает q, Q и M?

- Какие допущения положены в основу вывода формулы для определения нормальных напряжений при изгибе?

7. Сложное сопротивление

Основные сведения

При простых видах деформации (осевое растяжение или сжатие, сдвиг, кручение, плоский изгиб) в поперечных сечениях возникает только одно внутреннее усилие (продольная или поперечная сила, крутящий или изгибающий момент), за исключением плоского поперечного изгиба. На практике же большинство элементов конструкций и машин подвергается действиям сил, вызывающих одновременно не одну из указанных деформаций, а две и более. Различные комбинации простых деформаций называются сложным сопротивлением.

В общем случае нагружения бруса в его поперечных сечениях действуют шесть компонентов внутренних усилий (N, Q_x, Q_y, M_x, M_y, M_кр).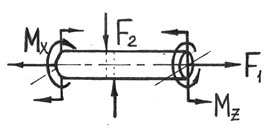



Рис. 7.1

Сложный вид деформации можно рассматривать как сумму простых видов, изученных ранее (растяжение, изгиб, кручение), при которых в сечениях элементов конструкций возникал только один внутренний силовой фактор (рис.7.2): нормальная сила N - при растяжении, изгибающий момент

М_z - при чистом изгибе, крутящий момент М_x - при кручении. Эти виды нагружения, растяжение, изгиб, кручение, являются простыми.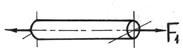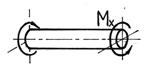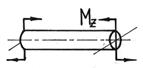



Рис.7.2

 

Основные соотношения, полученные для них, приведены в таблице 7.1

Таблица 7.1

Виды нагружения	Напряжения	Деформации
Растяжение	. Условие прочности:
Изгиб	Условие прочности:
Кручение	Условие прочности:

 

Но при сложном сопротивлении должен быть применим принцип независимости действия сил (частный случай принципа суперпозиции или наложения, применяемый в механике деформируемого твердого тела). 

Задачи на сложное сопротивление решаются следующим образом. Определяются напряжения и деформации при действии простейших видов деформации, составляющих сложное сопротивление, а затем полученные результаты суммируют, используя при необходимости теории прочности.

На практике одновременное действие всех силовых факторов встречается крайне редко. Чаще приходится иметь дело с более простыми комбинациями нагружений – косой или пространственный изгиб, внецентренное растяжение или сжатие и изгиб с кручением.