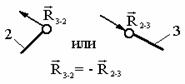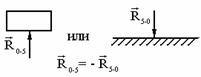24.05.05 Прикладная механика.. Учебное пособие по дисциплине Механика Модуль Прикладная механика

• Название: Учебное пособие по дисциплине Механика Модуль Прикладная механика
• Дата: 17.04.2023
• Размер: 1.89 Mb.
• Имя файла: 24.05.05 Прикладная механика..docx
• Тип: Учебное пособие; #1068488
• страница: 18 из 18

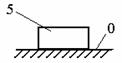
Рис. 9.29. Схема механизма

 

Функция положения – это аналитическая зависимость положения или координаты К-го звена ( , Х_К или Y_К ) от положения ведущего звена  , т.е.   или   и  , где  , X_K и Y_K – координаты, определяющие положение К-го звена (ведомого), а угол   – угол, характеризующий положение ведущего звена.

Аналог скорости. Угловая скорость К-го звена определяется зависимостью

,                                (3)

где   – аналог скорости К-го звена (первая передаточная функция) для вращающегося звена, величина безразмерная;  и  – аналоги скорости К-го звена, движущегося поступательно, величины безразмерные.

Аналог ускорения. Угловая скорость К-го звена определяется зависимостью, получаемой дифференцированием уравнения (3) по dt:

.

Введение в кинематический анализ понятий аналогов отделяет геометрические свойства механизма от кинематических.

Величину   называют ещё передаточным отношением, так как выражение   можно преобразовать, умножив и разделив его на величину dt:


Для решения задачи о положениях звеньев исследуемого механизма необходимо найти функции положения ( или Х_К и Y_К ), предварительно составив векторное уравнение замкнутого векторного контура кинематической цепи и уравнения проекций его на координатные оси Х и Y. Из этих уравнений находят функции положения (зависимости положений исследуемого звена от положения ведущего звена). При известном (заданном) законе движения ведущего звена задаются шагом и вычисляют координаты исследуемых звеньев (угловые координаты для вращающегося звена и прямоугольные для звена, совершающего возвратно-поступательное движение).

Для решения задачи о скоростях необходимо найти аналоги скоростей исследуемых звеньев и, умножив их на угловую скорость ведущего звена, получить формулы расчета искомых скоростей.

Для решения задачи об ускоренияхнаходят также аналоги ускорений звеньев и по формулам, приведенным в таблице, находят величины ускорений. Ниже приводится пример кинематического анализа кривошипно-ползунного механизма аналитическим методом.
9.5. Силовой (кинетостатический) анализ механизмов.
Проектирование нового механизма всегда включает его силовое исследование, так как по найденным силам производится последующий расчет на прочность элементов кинематических пар и звеньев механизма.

Силы, действующие в механизмах

Различают две группы внешних сил.

Движущие силы Р_дв или моменты движущих сил М_дв, которые:

- совершают положительную работу;

- направлены в сторону скорости точки приложения силы или под острым углом к ней;

- задаются посредством механической характеристики двигателя.

Пример: силы давления газа на поршень в двигателе внутреннего сгорания, силы веса при опускании груза и т.д.

Силы сопротивления Р_С и их моменты М_С, которые:

- совершают отрицательную работу;

- направлены противоположно скорости.

В свою очередь силы сопротивления делятся на силы:

- полезного сопротивления Р_п.с и моменты М_п.с (силы тяжести при подъеме груза);

- вредного сопротивления: трение в кинематических парах, сопротивление среды, внутреннее сопротивление (например, силы упругости звеньев).

Кроме этого существуют:

- силы веса (тяжести)  , где   – масса звена в кг;  м/с² – ускорение свободного падения. При кинематическом исследовании считают, что сила тяжести   приложена в центре тяжести звена. Если звено выполнено в виде стержня, то его ц.т. расположен в центре симметрии звена, а если в виде ползуна, то в центре шарнира. Силы тяжести в течении расчётного цикла могут быть как движущими, так и силами полезного сопротивления, поэтому работа этих сил за цикл равна нулю. Эти силы считаются внешними силами.

- силы инерции  ;

- моменты сил инерции  , где m, J_S – масса и массовый момент инерции звена;  и  – линейное и угловое ускорения;

- силы реакций в кинематических парах  , возникающие в опорах звеньев и являющиеся внутренними силами для механизма в целом и внешними для каждого отдельного звена.

Необходимо отметить, что под силами понимаются равнодействующие соответствующих распределенных в месте контакта кинематической пары нагрузок. Все вышесказанное относительно сил распространяется и на моменты сил.

 

Силы инерции звеньев и моменты сил инерции. 
Так как звенья механизма находятся в движении, и имеют свои массы, то, особенно в быстродействующих  механизмах рычажного типа, обязательно имеет место неравномерность движения звеньев. Это означает, что ускорения этих звеньев не равны нулю, что приводит к возникновению дополнительных сил динамического характера в виде сил инерции   и моментов инерции  . Из теоретической механики известно, что все силы инерции звена, совершающего плоскопараллельное движение и имеющего плоскость симметрии, параллельную плоскости движения, могут быть сведены к силе инерции  , приложенной в центре масс S звена, и паре сил инерции, момент которых обозначим   (рис. 9.30).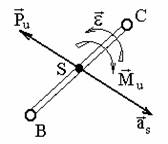



Рис. 9.30. Сила инерции звена и момента сил инерции

 

– главный вектор сил инерции, или сила инерции;

 – главный момент сил инерции, или момент сил инерции;m – масса звена;

 – массовый  момент  инерции  относительно центра  масс;

 – ускорение  центра  масс;

– угловое ускорение звена.

 и   направлены в стороны, противоположные ускорениям  и  .
Статическая определимость кинематической цепи

При силовом анализе механизмов (определении неизвестных сил, действующих на движущиеся звенья) можно использовать уравнения (законы) статики. Докажем это положение, проанализировав реакции в кинематических парах (табл. 9.2).

 Таблица 9.2.

Кинематические пары	Равновесие каждого звена	Известные параметры	Неизвестные параметры
5-й класс Вращательная		Точка приложения	Величина, направление
Поступательная		Направление	Величина, точка приложения
4-й класс		Точка приложения, направление	Величина

Примечание. 2, 3, 5 – номера звеньев.

 

В кинематических парах 5-го класса известно по одному параметру сил реакций, неизвестны два, в кинематических парах 4-го класса известны два параметра, а неизвестен один.

Таким образом, плоская кинематическая цепь, состоящая из кинематических пар 5-го и 4-го классов, имеет 2Р₅ + Р₄ неизвестных величин сил реакций.

В то же время для одного звена можно составить 3 уравнения статики, а для n звеньев – 3n уравнений статики.

Кинематическая цепь будет статически определима, если число неизвестных величин сил реакций не превышает числа возможных уравнений статики, т.е.

3n = 2P₅ + Р₄.

Это и есть условие статической определимости кинематической цепи.

Полученное равенство можно записать в виде

3n – 2Р₅ – Р₄ = 0.

Но запись слева от знака равенства является числом степеней свободы кинематической цепи W, т.е.

W = 3n – 2Р₅ – P₄ = 0.

Таким свойством (W=0) обладают структурные группы, или группы Ассура –статически определимые кинематические цепи.

 Силовой анализ механизма с учетом сил трения

9.6. Трение в механизмах. Виды трения.
Способность контактирующих поверхностей звеньев сопротивляться их относительному движению называется внешним трением. Трение обусловлено неидеальным состоянием контактирующих поверхностей (микронеровности, загрязнения, окисные пленки и т.п.) и силами межмолекулярного сцепления. Трение в кинематических парах характеризуется силами трения и моментами сил трения. Силой трения называется касательная составляющая реакции в кинематической паре (составляющая направленная по касательной к контактирующим поверхностям), которая всегда направлена против вектора скорости относительного движения звеньев.

Различают следующие виды трения:

- трение покоя проявляется в момент, когда два тела находящиеся в состоянии относительного покоя начинают относительное движение (касательную составляющую  возникающую в зоне контакта до возникновения относительного движения, в условиях когда она меньше силы трения покоя, будем называть силой сцепления; максимальная величина силы сцепления равна силе трения покоя);

- трение скольжения появляется в кинематической паре при наличии относительного движения звеньев; для большинства материалов трение скольжения меньше трения покоя;

- трение качения появляется в высших кинематической паре при наличии относительного вращательного движения звеньев вокруг оси или точки контакта;

- трение верчения возникает при взаимодействии торцевых поверхностей звеньев вращательных кинематической паре (подпятники).

Сила трения покоя зависит от состояния контактных поверхностей звеньев, а сила трения скольжения - также и от скорости скольжения.
 Теоретические основы определения коэффициента трения

Трение в поступательной кинематической паре

При перемещении одного тела (звена механизма) относительно находящегося с ним в контакте другого тела (звена) в месте их контакта возникает сила, сопротивляющаяся перемещению, – сила трения F (рис. 9.31).

Величину коэффициента трения в поступательной кинематической паре можно определить с помощью так называемого закона Кулона, в соответствии с которым величина силы трения F прямо пропорциональна нормальной силе N между соприкасающимися звеньями. Векторная сумма сил и   равна полной силе реакций в кинематической паре:   (рис. 30).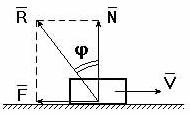



Рис. 9.31. Схема сил в поступательной кинематической паре

 

Отношение   называют коэффициентом трения скольжения в поступательной кинематической паре, а угол   – углом трения скольжения.

Полная реакция  отклоняется на угол трения   в сторону, противоположную скорости   (см. рис. 4.16).

Величину коэффициента трения скольжения f можно определить экспериментально или по справочникам (величина f зависит от шероховатости, материалов, трущихся поверхностей, наличия смазки, ее качества, температуры и т.д.).

 

Трение во вращательной кинематической паре
Внешние нагрузки, действующие на вал при его вращении, показаны на схеме рис. 9.32.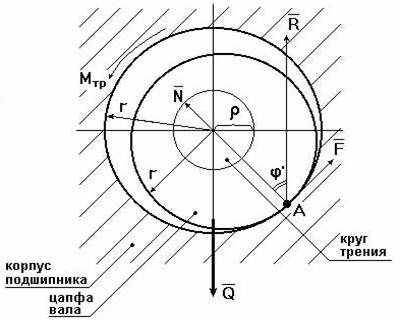



Рис. 9.32. Схема сил во вращательной кинематической паре
Здесь А – точка приложения нормальной реакции  , причем   – равнодействующая всех нормальных сил (эпюра этих сил может иметь различный вид), (рис. 32);  – сила трения (равно-действующая всех сил трения, распределенных по поверхности контакта); – сила давления цапфы вала на опору (корпус подшипника);   – сила реакции во вращательной  кинематической паре,  ;  ;   – угол трения; r – радиус цапфы (опорной части) вала;   – радиус круга трения;   – приведенный коэффициент трения.

Во вращательной кинематической паре реакция   отстоит от оси вращения на величину радиуса круга трения  , причем   всегда касательна к кругу трения.

Момент трения  .

Величину   можно определить:

– экспериментально (например, используя метод выбега);

– по эмпирическим формулам с учетом износа подшипника и соответствующего изменения эпюр давления (рис. 32): для нового подшипника  , для изношенного –  , где f – коэффициент трения скольжения в поступательной кинематической паре (берется из справочников).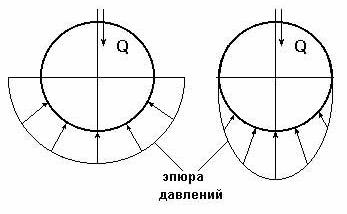

            



                           а)                                                          б)

Рис. 9.33. Примерные схемы эпюр давления в новом

(а) и изношенном (б) подшипниках скольжения

 

Трение качения в высшей кинематической паре
Картину внешних сил и эпюр распределения давлений в месте контакта тел качения можно условно отобразить на нижеприведенных схемах (рис. 9.34). В состоянии покоя эпюра напряжений в зоне контакта симметрична относительно общей нормали, проведенной через условную точку касания, а равнодействующая силаN совпадает с нормалью. При качении симметрия эпюры нарушается, а силаN смещается в направлении качения на расстояние k.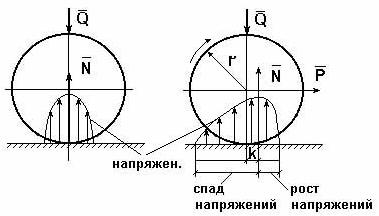

 



                    а)                                                         б)
Рис. 9.34. Примерные схемы сил и эпюр давления в зоне контакта цилиндра

с плоскостью: а) состояние покоя; б) состояние перекатывания

 

Здесь   – равнодействующая сила давлений в месте смятия соприкасающихся звеньев (тел качения);   – нагружающая сила, ;   – момент трения качения;   – плечо силы трения качения или коэффициент трения качения (имеет размерность длины);   – сила перекатывания.

Условие равновесия перекатывающегося тела в форме моментов можно записать как  , откуда  .

 
9.7. Динамика машин и механизмов.

 

Общие положения

Динамика - раздел механики машин и механизмов, изучающий закономерности движения звеньев механизма под действием приложенных к ним сил. Имеется такое определение: “Динамика рассматривает силы в качестве причины движения тел”. В основе динамики лежат три закона, сформулированные Ньютоном, из которых следует:

Из первого закона: Если равнодействующая всех внешних сил, действующих на механическую систему равно нулю, то система находится в состоянии покоя.

Из второго закона: Изменение состояния движения механической системы может быть вызвано либо изменением действующих на нее внешних сил, либо изменением ее массы.

Из этих же законов следует, что динамическими параметрами механической системы являются:

- инерциальные (массы mи моменты инерции I);

- силовые (силы F_ij и моменты сил M_ij);

- кинематические (линейные aи угловые   ускорения).

Динамическая модель - модель системы, предназначенная для исследования ее свойств в функции времени (или модель системы, предназначенная для исследования в ней динамических явлений).

Прямая задача динамики - определение закона движения системы при заданном управляющем силовом воздействии.

Обратная задача динамики- определение требуемого управляющего силового воздействия, обеспечивающего заданный закон движения системы.

Методы составления уравнений (динамической модели системы):

- энергетический (уравнения энергетического равновесия - закон сохранения энергия);

- кинетостатический (уравнения силового равновесия с учетом сил инерции по принципу Д’Аламбера).

Задачами динамического анализа и синтеза механизма, машины являются изучение режимов движения с учетом действия внешних сил и установление способов, обеспечивающих заданные режимы движения. При этом могут определяться мощности, необходимые для обеспечения заданного режима движения машины, проводиться сравнительная оценка механизмов с учетом их механического коэффициента полезного действия, устанавливаться законы движения ведущего звена (например, колебания угловой скорости кривошипа за один оборот) под действием внешних сил, приложенных к звеньям механизма, а также решаться задачи подбора оптимальных соотношений между силами, массами, размерами звеньев механизмов.

В динамике машин объектом изучения (исследования) является машинный агрегат. В общем виде его можно представить как механическую систему, состоящую из трех основных частей: машина-двигатель, передаточный механизм и рабочая машина (или исполнительный механизм).

В машине-двигателе какой-либо вид энергии преобразуется в механическую энергию, необходимую для приведения в движение рабочей машины. Например, в электродвигателе электрическая энергия преобразуется в механическую, а в двигателе внутреннего сгорания в механическую энергию преобразуется тепловая энергия сгорания топлива.

Передаточный механизм служит для преобразования движения, изменения характера движения, скорости, направления движения и т.д.

Рабочая машина предназначена для выполнения работы, связанной с трудовой деятельностью человека или выполнением технологического процесса.

Работа – физическая величина, характеризующая преобразование энергии из одной формы в другую.

Элементарная работа силы выражается формулой

где Р – сила; dS – элементарная величина перемещения точки приложения силы;   – угол между векторами силы и скорости.

Элементарная работа момента силы выражается формулой

,

где М – момент силы;   – элементарный угол поворота.

Размерность работы измеряется в джоулях: Дж = Нм.

Полная работа выражается формулами

, или  .

Мощность – это энергетическая характеристика, равная отношению работы к интервалу времени ее совершения, выражается формулами

,

где V – скорость точки приложения силы Р,

или  ,

где  – угловая скорость звена, к которому приложен момент.

Размерность мощности измеряется в ваттах: Вт = Дж/c; 1000 Вт =1 кВт (киловатт), 1 кВт = 1, 36 л.с.

Кинетическая энергия, приведенная масса, приведенный момент инерции механизма

Анализ движения машинного агрегата, находящегося под действием приложенных к нему внешних сил, удобно проводить с использованием метода приведения масс и сил к какому-либо звену механизма. Он сводится к анализу динамики тела (звена приведения), к которому приведены все внешние силы и моменты. Чаще всего звеном приведения выступает ведущее звено механизма.

Задача динамического анализа – определение истинного закона движения ведущего звена механизма, находящегося под действием заданных внешних сил и моментов, действующих в машинном агрегате.

 

Кинетическая энергия механизма
Для i-го звена, совершающего сложное движение (например, для шатуна кривошипно-ползунного механизма), кинетическую энергию можно выразить формулой

,

где первое слагаемое правой части – это кинетическая энергия поступательного движения центра масс звена; второе слагаемое – кинетическая энергия вращательного движения; m_i – масса звена; V_si – скорость центра масс; J_si – момент инерции звена относительно центра масс;   – угловая скорость звена.

Для всего механизма кинетическая энергия равна сумме кинетических энергий всех звеньев механизма:

(1)

где n – количество подвижных звеньев.
Приведенная масса механизма
Условно заменим механизм его динамической моделью. Например, кривошипно-ползунный механизм (рис. 9.35) заменим динамической моделью, состоящей из стойки и кривошипа.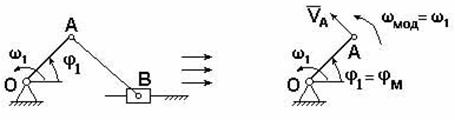



Рис. 9.35. Замена кривошипно-ползунного механизма динамической моделью

 

Здесь ОА – звено приведения механизма, в котором как бы сосредоточена инертность всех звеньев механизма, А – точка приведения.

Уравнение (1) умножим и разделим на квадрат скорости точки приведения V_A: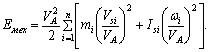



Выражение в квадратных скобках имеет размерность массы (кг) и называется приведенной массой m_пр механизма в точке А.

Тогда

где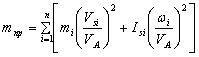

.                                   (2)

Приведенной массой механизма называется такая условная масса, которая как бы сосредоточена в точке приведения механизма, кинетическая энергия которой равна сумме кинетических энергий всех звеньев механизма.

 

Приведенным моментом инерции механизма называется такой условный момент инерции, которым как бы обладает звено приведения относительно оси вращения, кинетическая энергия которого (при таком моменте инерции) равна сумме кинетических энергий всех звеньев механизма.

Величины m_пр и J_пр не являются постоянными для данного механизма, а меняют свое численное значение в зависимости от положений звеньев, так как звенья меняют свои скорости.

 

Пример 1.

Определить приведенную массу и приведенный момент инерции для заданного положения кривошипно-ползунного механизма (рис. 35), если известны положения центров масс звеньев (S₁ и S₂), линейные и угловые скорости звеньев и центров масс звеньев:  ,   и   – скорости центров масс кривошипа, шатуна и ползуна,   и   – угловые скорости кривошипа и шатуна.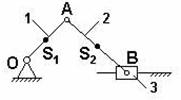



Рис. 9.36. Кривошипно-ползунный механизм

 

Пусть кривошип 1 – звено приведения, А – точка приведения.

Приведенная масса механизма согласно (4.2) вычисляется по формуле

,

а приведенный момент инерции согласно (3) – по формуле

.
Уравнение движения машины в форме кинетической энергии
Рассмотрим состояние механизма при двух различных положениях ведущего звена, разделяемых каким-либо промежутком времени   или углом   поворота ведущего звена – кривошипа (рис. 9.37).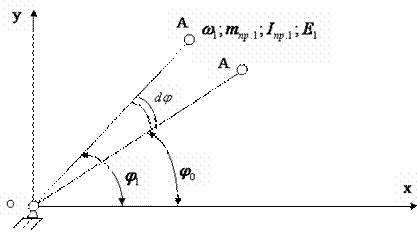



Рис. 9.37. Кинематические и динамические параметры механизма

при различных положениях звена приведения

 

При положении кривошипа   угловая скорость звена приведения –  , I_пр.0 – приведенный момент инерции механизма в рассматриваемом положении.

При положении   угловая скорость звена приведения –  , I_пр.1 – приведенный момент инерции механизма.               

Изменение кинетической энергии механизма   за этот промежуток времени будет равно разности работ сил движущих А_дв и сил сопротивления  А_сопр, выполненных за это время (или избыточной работе  ):

.           (4)

(5)

где Е₀ и Е₁ – величины кинетических энергий механизма при положениях   и   кривошипа.

(6)

(7)

где М_дв и М_сопр – приведенные моменты сил движущих и сил сопротивлений.

Подставив (5-7) в (4), получим

.                                         (8)

Из (8) выразим угловую скорость кривошипа при положении  :

                                               (9)

Уравнение (9) называют уравнением движения машины в форме кинетической энергии.

 

Режимы движения машины
В общем виде движения машины можно разделить на три основных режима (периода): разгон, установившееся движение и останов (рис. 9.38).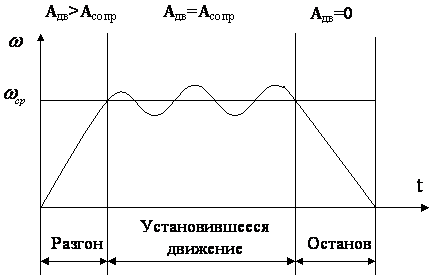


Рис 9.38. Схема режимов движения машины

 

В режиме разгона угловая скорость в начале режима  , в конце –   , что следует из уравнения (9). При этом всегда  , иначе разгон невозможен.

В режиме установившегося движения  , изменение кинетической энергии (в среднем за один оборот ведущего вала)  . В пределах одного оборота происходят периодические колебания угловой скорости вала машины.

В режиме останова (когда двигатель отключен)  . При этом выполняется работа, затрачиваемая на преодоление сил трения:   

 

9.8. Механический кпд механизма
В период установившегося движения машины соблюдается условие равенства работ сил движущих и сил сопротивлений:

.

Работа сил сопротивления складывается из суммы работ сил полезного сопротивления   и сил вредного сопротивления  . Тогда

.

Разделим левую и правую части равенства на величину работы сил движущих:

и получим

где  – механический (цикловой) коэффициент полезного действия (кпд);    – коэффициент механических потерь.

 

Определение кпд машинного агрегата при последовательном соединении входящих в него механизмов
Рассмотрим машинный агрегат, состоящий из последовательно соединенных механизмов, условно обозначенных на схеме (рис. 9.39) цифрами 1, 2 и 3.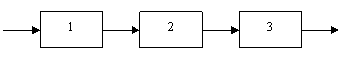



А                         А₁                               А₂                             А₃
Рис. 9.39. Машинный агрегат с последовательно соединенными механизмами

 

Пусть к механизму 1 подводится работа величиной А. На выходе получаем работу величиной А₁, которая подводится к механизму 2 и т.д. Величина работы на выходе всегда меньше, чем подведенная работа на входе (А₁<A, A₂<A₁, A₃<A₂), так как в каждом механизме имеются механические потери подведенной к нему работы.

Тогда общий кпд машинного агрегата

а кпд каждого механизма

,     ,     .

Перемножим кпд всех последовательно соединенных механизмов:



Вывод: общий механический кпд машинного агрегата, состоящего из последовательно соединенных n механизмов, равен произведению их кпд:

Определение кпд машинного агрегата при параллельном соединении входящих в него механизмов

Рассмотрим машинный агрегат, состоящий из трех параллельно соединенных механизмов, условно обозначенных на схеме (рис. 9.40) цифрами 1, 2, 3. Пусть к механизмам подводится работа величиной А, которая распределяется на каждый механизм в разных долях, определяемых коэффициентами  ,  ,  , каждый из которых меньше 1, а их сумма  .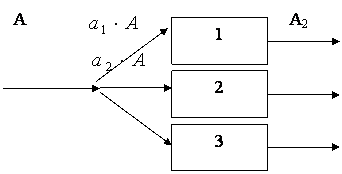



Рис. 9.40. Машинный агрегат с параллельно соединенными механизмами

 

Общий кпд всего машинного агрегата можно выразить отношением суммы работ на выходе механизмов к общей подведенной работе А:

.                                           (12)

Так как

,  ;

,  ;

,  ,

то, подставив эти выражения в (12), получаем

.

Отсюда следует, что общий механический кпд машинного агрегата при параллельном соединении механизмов равен сумме величин кпд каждого механизма, умноженных на коэффициенты долей работ, подводимых к механизмам:

.

Сравним варианты последовательного и параллельного соединения механизмов с точки зрения минимизации механических потерь в машинном агрегате.

Пусть величины кпд каждого механизма равны  . При этом коэффициенты, учитывающие доли распределения общей работы А между всеми механизмами, также равны:

.

Тогда

,  .

Так как  , то  . Отсюда следует, что параллельное соединение механизмов в машинном агрегате предпочтительнее с точки зрения уменьшения механических потерь.

 

Самоторможение
Если  , то действительного движения механизма произойти не может. Это называется явлением самоторможения. Следовательно, если при теоретических расчетах получим  , то механизм в заданном направлении двигаться не может.

Для возможности движения механизма необходимо обеспечить условие

.

Неравномерность хода ведущего звена машины
Уравнение движения главного вала машины в форме кинетической энергии имеет вид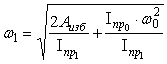

.

Так как величина избыточной работы  , являясь функцией угла поворота вала  , угловой скорости   и времени t, есть величина переменная, т.е.  ,при этом  ,то при установившемся режиме работы машины угловые скорости в начале и конце одного цикла Т (например, одного оборота) равны:  (рис. 40).

За цикл изменение кинетической энергии равно нулю  . Внутри цикла угловая скорость вала может меняться, что вызывает дополнительные динамические (инерционные) нагрузки, а также дополнительное трение в кинематических парах, снижающее надежность механизма и его кпд.

Ухудшаются условия работы механизма, приходится увеличивать материалоемкость машины, повышать прочность звеньев, нести дополнительные энергетические затраты на преодоление трения.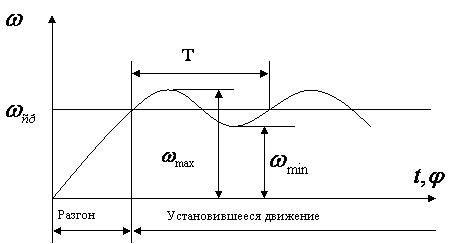


Рис. 9.41. Периодические колебания угловой скорости главного вала машины в период установившегося движения

 

Коэффициент неравномерности хода ведущего вала машины   выразим формулой

,                                                    (13)

где

.                                               (14)  

Из (13) и (14) получим

Величинаможет находиться в следующих пределах: для ударных машин и прессов  , для металлорежущих станков  , для двигателей  .

 

9.9. Регулирование периодических колебаний угловой скорости с помощью маховика
В случае необеспечения требуемой величины   при работе машины могут возникнуть нежелательные явления и процессы (вибрация, повышенные энергетические затраты, невозможность выполнения технологического процесса и т.д.). При условии периодических колебаний угловой скорости вала для получения заданной величины   используют маховик – массивное колесо с большим моментом инерции.

Основная задача при расчете маховика – это определение его момента инерции. Маховик с таким моментом инерции   в интервале скоростей от  до   (см. рис. 5.5) должен произвести работу, равную изменению кинетической энергии механизма за это время:

.

 

Расчет величины момента инерции маховика
Приведенный момент инерции механизма можно представить в виде

при  ,

при  ,

где  – постоянная составляющая приведенного момента инерции механизма;   – момент инерции маховика или маховых масс (колес, валов и т.д.), (величина постоянная для данного механизма);  – составляющая приведенного момента инерции при максимальной скорости в цикле  ;  – составляющая приведенного момента инерции при минимальной скорости в цикле  .

Тогда

.                                     (15)

Из (15) следует (если  ,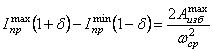 

.

С учетом (13) и (14) получим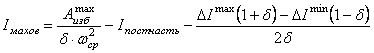

.          (16)

Для определения величины   задаются величинами   и  . Формулу (16) можно упростить, если принять  . Тогда

.

При больших маховых массах (когда  ) можно приближенно принять

.

Для определения величины   можно пользоваться диаграммами моментов сил движущих   и сил сопротивлений   (рис. 9.42).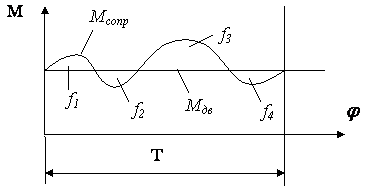


Рис. 9.42. Моменты сил движущих и сил сопротивлений в цикле Т

 

Площади f₁…f₄, ограниченные кривой М_сопр и графиком М_дв, представляют собой разности работ движущих моментов М_дв и моментов сопротивлений М_сопр. Суммы площадей имеют соотношение 

Выбирают наибольшую из заштрихованных площадей. Если  , то величину максимальной избыточной работы можно определить по формуле

,

где   и  – масштабы графиков по осям   и М.
Регулирование непериодических колебаний скорости движения машин
В процессе выполнения работы приходится регулировать скорость рабочего органа машины. Например, в стационарных двигателях необходимо поддерживать скорость рабочего органа постоянной, а в двигателях транспортных машин эта скорость должна изменяться в широких пределах.

Из уравнения движения машины следует, что изменения скорости рабочего органа можно достигнуть за счет изменения разности работ движущих сил и сил сопротивления  ( ). 

Устройства, обеспечивающие изменения работы сил сопротивления применяются в виде тормозов, например, в транспортных машинах, которые снабжаются также и приспособлениями для одновременного разобщения двигателя с машиной – орудием.

Другим способом регулирования является изменение работы движущих сил путем воздействия на орган, подающий энергию к входному звену (поршню у двигателя внутреннего сгорания, лопаткам турбины и т.д.).

Регулирование может осуществляться либо человеком-оператором, либо автоматически – с помощью устройств, называемых регуляторами.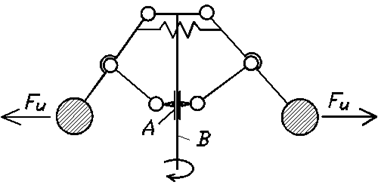



                                                

Рис. 9.43

 

Одним из них является центробежный регулятор (рис.42), приводимый во вращение валом двигателя В. Ползун А соединяется с органом, подводящим рабочее тело (пар, горючая смесь и т.д.). Регулятор автоматически поддерживает скорость вала двигателя постоянной, т.к. ее увеличение приводит к уменьшению подачи рабочего тела и наоборот.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
- Что является целью курса ТММ, какие задачи решаются в курсе ТММ?

- Какие основные разделы содержит курс ТММ?

- Что называется "проектом" и "инженерным проектированием"?

- Перечислите основные этапы процесса проектирования?

- Дайте определения понятий "техническая система" и "структура"?

- Что называется "машиной", какие виды машин Вы знаете?

- Дайте определения понятий "звено" и "кинематическая пара"?

- Какая техническая система называется механизмом?

- Почему вращательное движение наиболее распространено в механизмах и машинах?

- Какие функции могут выполнять механические передачи?

- Какие механизмы называют рычажными?

- Какие звенья всегда входят в состав шарнирных механизмов?

- Чем кривошип отличается от коромысла?

- В чем особенность зубчатой передачи и кулачкового механизма?

- Что такое кулачок?

- Что такое передаточное число?

- Как определяют передаточное число и КПД многоступенчатой передачи?

- Как изменяются от ведущего к ведомому валу такие характеристики передачи как мощность, вращающий момент, частота вращения?

- В какой форме может быть представлена структурная модель механизма?

- Какова цель структурного анализа?

- Что понимают под логическими приемами анализа и синтеза?

- Что называют звеном механизма?

- Что называют кинематической парой?

- Как классифицируются плоские кинематические пары?

- Что называется кинематической цепью?

- Как рассчитать подвижность плоского механизма?

- Какой физический смысл имеет подвижность механизма?

- Что собой представляет избыточная связь?

- Перечислите признаки по которым классифицируются кинематические пары?

- Что называют структурным анализом и структурным синтезом?

- Каким образом при выборе структурной схемы механизма учитываются ее функциональные возможности?

- Какие избыточные связи полезны для работы механизма?

- Чем кинематическая пара отличается от других подвижных соединений двух звеньев?

- Какими преимуществами и недостатками обладают низшие пары по сравнению с высшими?

- Напишите формулы для подсчета подвижности механизма для плоскости и для пространства?

- Как из кинематической цепи получить механизм?

- Чему равно минимальное число звеньев и кинематических пар в кинематической цепи?

- Что называется "функцией положения" для звена или точки механизма?

- В чем различие между кинематическими и геометрическими характеристиками механизма?

- Какие функции называются кинематическими передаточными функциями механизма?

- Какие передаточные функции механизма называются главными, а какие вспомогательными?

- Перечислите методы геометро-кинематического исследования механизмов?

- Что называется "центроидой", как центроиды используются при кинематическом исследовании механизма?

- Как метод кинематических диаграмм применяется при кинематическом исследовании механизмов?

- Как применяется метод преобразования координат при решении прямой задачи о положении точки выходного звена?

- Опишите последовательность кинематического анализа плоского механизма.

- По какому признаку можно установить, является ли равномерным (или неравномерным) относительное движение звеньев, образующих поступательную пару?

- Дайте классификацию сил, действующих в кинематических парах механизмов?

- Перечислите виды силового расчета механизмов?

- Как определить число неизвестных в силовом расчете?

- Назовите цели и методы силового анализа механизма.

- Сформулируйте условие статической определимости плоского механизма.

- Что изучается в разделе курса динамика машин и механизмов?

- Как формулируются прямая и обратная задачи динамики машин?

- Что называется "энергией", "работой" и "мощностью"?

- Как идеальные механизмы преобразуют энергию?

- Что называют коэффициентом полезного действия механической системы ?

- Как определяется КПД механической системы при последовательном и параллельном соединении элементов ?

- Какой режим движения машины называется установившимся ?

- Что называется "коэффициентом неравномерности" и какие величины этого коэффициента установлены для различных машин?

- Какими методами регулируется величина "коэффициента неравномерности" ?

- Как влияет момент инерции маховика на коэффициент неравномерности ?

- Как по коэффициенту неравномерности определяется необходимая маховая масса первой группы звеньев ?

- Изложите алгоритм решения задачи регулирования хода машины по методу Н.И. Мерцалова ?

- По каким зависимостям рассчитываются первые передаточные функции кривошипно-ползунного механизма ?

- Как определяются параметра динамической модели для двигателя внутреннего сгорания ?

- Как строится диаграмма кинетической энергии второй группы звеньев ?

- Как строится диаграмма угловой скорости звена приведения ?

- Как учитывается статическая характеристика асинхронного электродвигателя при анализе динамических процессов ?

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. 
   Александров А.В. и др. Сопротивление материалов: Учебник для ст-тов вузов – 2-е изд., испр. – М.: Высшая школа, 2008. – 559 с.
   
2. 
   Бояршинов, С.В. Основы строительной механики машин – М. : Машиностроение, 2006. – 456 с.
   
3. 
   Гафаров Р.Х. Что нужно знать о сопротивлении материалов: Учебное пособие для вузов обуч. по направлениям подгот. и спец. в области техники и технологии – М.: Машиностроение, 2007. – 275 с.
   
4. 
   Дарков, А.В. Сопротивление материалов. – М. : Высшая школа, 2007. – 623 с
   
5. 
   Миролюбов И.Н. и др. Пособие по решению задач по сопротивлению материалов: учебное пособие для технических вузов. – М.: Высшая школа, 2007. – 399 с
   
6. 
   Степин П.А. Сопротивление материалов. – М. : Высшая школа, 2008. – 303 с.
   
7. 
   Феодосьев В.И. Сопротивление материалов: Учебник для студ-ов высш. техн. учеб.зав. – 10-е изд., перераб. и доп. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2008. – 588 с.