24.05.05 Прикладная механика.. Учебное пособие по дисциплине Механика Модуль Прикладная механика

• Название: Учебное пособие по дисциплине Механика Модуль Прикладная механика
• Дата: 17.04.2023
• Размер: 1.89 Mb.
• Имя файла: 24.05.05 Прикладная механика..docx
• Тип: Учебное пособие; #1068488
• страница: 9 из 18

4. Геометрические характеристики плоских сечений

Сопротивление стержня различным видам деформирования часто зависит не только от его материала и размеров, но и от характера осевой линии, формы поперечных сечений и их ориентации.

Уже в древности строители знали, что доска или брус, поставленные на ребро, во много раз лучше противостоят изгибу, чем положенные плашмя. Речь идет как об их несущей способности, так и о деформативности. Для двутавровой стандартной балки, поставленной на две опоры, эти показатели примерно в 7 и 30 раз выше, чем у балки квадратного поперечного сечения такой же площади, cделанной из того же материала. Таким образом, рациональное расположение материала по сечению позволяет снизить его расход.

Как увидим дальше, этот вывод имеет обобщение на форму конструкции в целом. Но в данный момент, отвлекаясь от физических свойств изучаемого объекта, рассмотрим основные геометрические характеристики поперечных сечений стержня, определяющие сопротивление различным видам его деформирования.

В расчетах конструкций на механическую надежность очень часто приходится оперировать такими характеристиками плоских фигур, как статический момент, осевой и полярный моменты инерции. Хотя вычисление вышеназванных геометрических характеристик относится к числу простейших задач интегрального исчисления, тем не менее, в силу их узкого прикладного значения они практически не рассматриваются во втузовском курсе высшей математики. По установившейся традиции геометрические характеристики плоских фигур изучаются в курсе сопротивления материалов.

Геометрические характеристики – числовые величины (параметры), определяющие размеры, форму, расположение поперечного сечения однородного по упругим свойствам деформируемого элемента конструкции (и, как следствие, характеризующие сопротивление элемента различным видам деформации).
4.1.Статические моменты сечения
Статическим моментом плоского сечения относительно некоторой оси называется, взятая по всей его площади А, сумма произведений площадей элементарных площадок dA на их расстояния от этой оси (рис. 4.1):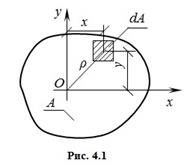

 



 







где y_c– расстояние от центра тяжести всего плоского сечения до оси x; x_c – расстояние от центра тяжести всего сечения до оси y.

Статический момент  сложного сечения относительно некоторой оси равен сумме статических моментов всех частей этого сечения относительно той же оси:

 



В формулах (6) введены обозначения: А₁, А₂, …, А_n – площади простых элементов, составляющих плоское сложное сечение; x₁, y₁, x₂, y₂, x₃,y₃, … , x_n, y_n – координаты центров тяжести простых составляющих сложного плоского сечения относительно выбранных осей х и у.

Из выражений (4) можно определить координаты центра тяжести плоского сечения:



Для сложного поперечного сечения формулы (7) можно представить в следующем виде





Зависимости между статическими моментами одного и того же сечения относительно двух параллельных друг другу осей х и х₁, а также у и у₁ имеют вид:



где параметры a, b показаны на рис. 4.2.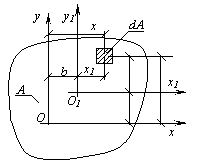



Рис.4.2

 

У к а з а н и я.

1. Изменение положительного направления оси у вызывает изменение знака статического момента S_x. Аналогично, изменение положительного направления оси х вызывает изменение знака статического момента S_y. 

2. Статический момент сечения равен нулю относительно любой оси, проходящей через центр тяжести этого сечения.

3. Если плоское сечение имеет ось симметрии, то эта ось всегда проходит  через  центр  тяжести плоского сечения, а поэтому, согласно п.2, статический момент сечения относительно оси симметрии всегда равен нулю.

4. Если плоское сечение имеет две оси симметрии, то центр тяжести сечения лежит на пересечении этих осей симметрии.

4.2. Моменты инерции плоских сечений простой формы.
В дополнение к статическим мо­ментам в системе координат x0y рассмотрим три интегральных выражения:







Первые два интегральных выраже­ния называются осевыми моментами инерции относительно осей x и y, а третье  центробежным моментом инерции сечения относительно осей x, y.

Для сечений, состоящих из n-числа областей (рис. 4.3), фор­мулы (10) будут иметь вид:









Рис. 4.3.

 

4.3. Моменты инерции плоских сечений простой формы
В дополнение к статическим мо­ментам в системе координат x0y рассмотрим три интегральных выражения:







Первые два интегральных выраже­ния называются осевыми моментами инерции относительно осей x и y, а третье  центробежным моментом инерции сечения относительно осей x, y.

Для сечений, состоящих из n-числа областей (рис. 4.4), фор­мулы (10) будут иметь вид:









Рис. 4.4

 

где    радиусвектор точки тела в заданной полярной системе ко­ординат.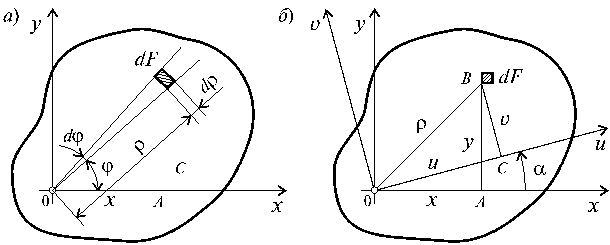

 



Рис. 4.5

 

Вычислим полярный момент инерции круга радиуса R. На рис. 4.5, a показана элементарная площадка, очерченная двумя ра­диусами и двумя концентрическими поверхностями, площадью

Интегрирование по площади заменим двойным интегрировани­ем:



Hайдем зависимость между полярным и осевыми моментами инерции для круга. Из геометрии видно (рис. 4.5, б), что

следовательно,



Данное условие называется условием инвариантности. Формулируется условие инвариантности следующим образом: сумма осевых моментов инерции относительно двух любых взаимно перпендикулярных осей есть величина постоянная и равная полярному моменту инерции относительно точки пересечения этих осей.

Так как оси x и y для круга равнозначны, то 

Полярный момент инерции кольца может быть найден как разность моментов инерции двух кругов: наружного (радиусом R) и внутреннего (радиусом r):



Размерность моментов инерции L⁴. Осевые и полярные моменты инерции всегда положительны, центробежный момент инерции может быть положительным, отрицательным, равным нулю.

Для фигур, имеющих более двух осей симметрии, осевые моменты инерции относительно всех центральных осей равны между собой. К таким фигурам относятся равносторонний треугольник, квадрат, круг и т.д.

 

Моменты инерции простых сечений

Вычислим моменты инерции простейших фигур.

 

Прямоугольник (рис. 4.6)

Определим моменты инерции относительно осей, совпадающих со сторонами, и относительно центральных осей (рис.4.6).

По определению 



Рис. 4.6

 

Элемент площади равен   dA=bdy,

следовательно 

По формуле  , откуда, учитывая что   А = bh, y_c = 0,5h,   находим



Аналогично получим    и  

 

Треугольник (рис. 4.7)

Момент инерции относительно оси х, cовпадающей с основанием,



Но   dA = b(y)dy,   b(y) = (b/h)(h-y).

Cледовательно,





Рис. 4.7

 

По формуле параллельного переноса  ,  откуда



 

Круг (рис. 4.8)

Для  любых  центральных  осей   ,  поэтому  

Как известно, полярный момент инерции круга равен 



Рис. 4.8

 

Следовательно, 

 

Кольцо    (рис. 4.9)

Момент инерции относительно оси   (рис.4.9) можно определить как разность моментов инерции наружного и внутреннего круга:



Для тонкого кольца существует приближенная формула 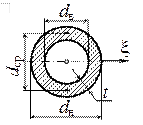 , где   d_ср – средний диаметр, t - толщина кольца.



Рис. 4.9

 

Моменты инерции сечений сложной формы
Момент инерции сечения сложной формы относительно некоторой оси равен сумме моментов инерций его составных частей относительно той же оси:



что непосредственно следует из свойств определенного интеграла. Таким образом, для вычисления момента инерции сложной фигуры надо разбить ее  на ряд простых фигур, вычислить моменты инерции этих фигур, а затем просуммировать их.

 

4.3. Моменты сопротивления
Осевой момент сопротивления относительно рассматриваемой оси – величина равная моменту инерции относительно той же оси отнесенному к расстоянию до наиболее удаленной от этой оси точки





Полярный момент сопротивления



Осевой и полярный моменты инерции имеют размерность м³.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

- Что называют поперечным сечением стержня?

- Для чего необходимы геометрические  характеристики плоских сечений?

- Что такое статический момент плоской фигуры? Какова его размерность?

- Какими свойствами обладает статический момент?

- Относительно каких осей статический момент равен нулю?

- Какую размерность имеет статический момент сечения?

- Как определяется положение центра тяжести сечения?

- Как определяются координаты центра тяжести сложного сечения?

- Что понимается под осевым, полярным и центробежным моментами инерций? Какими свойствами они обладают? Их размерность?

- Что такое полярный момент инерции?

- Размерность моментов инерции сечения?

- Как записываются формулы перехода для моментов инерции при параллельном переносе осей?

- Чему равен осевой момент инерции относительно центральной оси?

- Чему равен осевой момент инерции для круга и кольца?

- Получите соотношение между осевыми и полярными моментами инерции сечения?

- Что такое момент сопротивления сечения? Чему он равен для прямоугольного и круглого сечения?

- Чему равен центробежный момент инерции относительно главных осей  инерции?

- Какие центральные оси  являются главными у сечений, имеющих более двух осей симметрии?

- Почему производят разбивку сложного сечения на составляющие простые части при определении статических моментов и моментов инерции сечения?

- Какие оси называются центральными осями ?