24.05.05 Прикладная механика.. Учебное пособие по дисциплине Механика Модуль Прикладная механика

• Название: Учебное пособие по дисциплине Механика Модуль Прикладная механика
• Дата: 17.04.2023
• Размер: 1.89 Mb.
• Имя файла: 24.05.05 Прикладная механика..docx
• Тип: Учебное пособие; #1068488
• страница: 4 из 18

Рис. 1.7. Виды сопротивлений:

а) растяжение (сжатие); б) сдвиг; в) кручение; г) изгиб

 

Согласно принятому правилу знаков для изгибающего момента, если внешняя сила, приложенная к рассматриваемой части бруса изгибает участок, расположенный между сечением точкой ее приложения выпуклостью вниз, то изгибающий момент положительный. Отрицательному значению изгибающего момента соответствует противоположное направление выпуклости балки

Таким образом, метод сечений позволяет найти значения внутренних силовых факторов и установить вид нагружения в любом сечении бруса при действии любой нагрузки. Для этого необходимо выполнить следующее:

1. Мысленно рассекаем брус на две части в пределах исследуемого i–го участка.

2. Оставляем ту часть бруса, на которую действует меньше сил.

3. Заменяем действие условно отброшенной части бруса положительными внутренними силовыми факторами, приведенными к центру тяжести исследуемого сечения бруса.

4. Выберем для оставленной части бруса скользящую систему координат (начало координат совмещаем с границей участка, положение исследуемого сечения определяется координатой z_i, где 0≤z_i≤c и c – длина i-го участка).

5. Определяем искомые внутренние силовые факторы из уравнений равновесия ΣZ = 0;  ΣY = 0;   ΣX = 0;   Σm_z = 0;   Σm_y = 0;   Σm_x = 0, которые составляем для оставленной части бруса.

Проверка правильности определения усилий ведется в двух направлениях:

а) выполнение условий равновесия, не использованных при определении внутренних усилий;

б) проверка равновесия части тела, которая не рассматривалась при решении задачи.

В зависимости от вида внутренних силовых факторов, возникающих в сечении, различают различные следующие виды нагружениябруса.

- Растяжение или сжатие. Действует только продольная сила N.

- Кручение. Действует только крутящий момент T.

- Сдвиг. Действует  только поперечная сила Q_x или Q_y

- Изгиб. Действует только изгибающий момент M_x или M_y(чистый изгиб), при действии изгибающего момента и поперечной силы (поперечный изгиб).

- Сложное сопротивление. Одновременное действие нескольких силовых факторов. Например, M_x и T, M и N.

Итак, внутренние усилия в сечении есть функции параметров, определяющих положение сечения в теле, и нагрузок по одну сторону от сечения. Эти функции могут быть представлены аналитически или графически. График, показывающий изменение внутреннего усилия в зависимости от положения сечения, называется эпюрой. Ординаты усилий в определенном масштабе откладывают от линии, соответствующей оси бруса.

3. Дифференциальные уравнения равновесия для внутренних усилий в поперечных сечениях стержней

В общем случае нагрузка на стержень может быть задана интенсивностью сил с составляющими n, q_y, q_z, и интенсивностью моментов с составляющими t, m_y, m_z. Возможна также нагрузка, сосредоточенная в отдельных точках. Для бесконечно малой части стержня (рис.8) составим дифференциальные уравнения равновесия.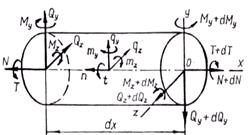



Рис. 1.8

 

Из условий ΣX=0,  ΣY=0,  ΣZ=0,  ΣM_x=0, следуют уравнения:

Из условий ΣX=0,  ΣY=0,  ΣZ=0,  ΣM_x=0, следуют уравнения:



Из условий ΣM_y=0, ΣM_z=0 получаем:





откуда, пренебрегая бесконечно малыми второго порядка, находим



Подставляя выражения Q_y и Q_z в соответствующие дифференциальные уравнения, получаем



Интегрируя полученные шесть уравнений, находим выражения для внутренних усилий:













Постоянные интегрирования С_i (i=1,2,...,6) определяются из граничных условий для рассматриваемых внутренних усилий.

Поскольку дифференциальные уравнения выражают равновесие любого бесконечно малого элемента стержня, то удовлетворение им означает выполнение условий равновесия стержня в целом.

Дифференциальные зависимости используются для проверки результатов, полученных с помощью алгебраических уравнений равновесия. Они позволяют, например, по эпюре M_z(M_y) определить характер эпюры Q_y(Q_z). В частности, на участках, где m_z=0 (m_y=0), т.е. при соблюдении зависимостей



можно установить, что при М_z = const имеем Q_y= 0(при М_y=const имеем Q_z = 0). Переменная величина M_z(M_y) достигает экстремальных значений в точках, где Q_y= 0(Q_z= 0).

При определении внутренних усилий из уравнений равновесия целесообразно нагрузку на поверхности переносить в соответствующие точки на оси стержня с соблюдением условий статической эквивалентности. Полученная таким образом силовая схема является составной частью так называемой расчетной схемы (системы), когда брус представляется его осью. 

3. 
   Допущения, применяемые в сопротивлении материалов
   

Для построения теории сопротивления материалов принимают некоторые понятия и допущения относительно структуры и свойств материалов, а также о характере деформаций. Приведем основные из них.

1. В сопротивлении материалов принято рассматривать все материалы как однородную сплошную среду, независимо от их микроструктуры.

Под однородностью материала понимают независимость его свойств от величины выделенного из тела объема. И хотя в действительности реальный материал, как правило, неоднороден (уже в силу его молекулярного строения), тем не менее, указанная особенность не является существенной, поскольку в сопротивлении материалов рассматриваются конструкции, размеры которых существенно превышают не только межатомные расстояния, но и размеры кристаллических зерен.

С понятием однородности тесно связано понятие сплошности среды, под которым подразумевают тот факт, что материал конструкции полностью заполняет весь отведенный ему объем, а значит в теле конструкции нет пустот и не учитывается реальная структура материала (зернистая, кристаллическая и др.). Это допущение позволяет использовать в сопротивлении материалов методы математического анализа (дифференциальное и интегральное исчисления). Для большинства машиностроительных конструкций расчеты, основанные на допущении о сплошности строения дают 

практически удовлетворительные результаты. Это объясняется тем, что размеры детали во много раз больше межатомных расстояний.

2. Обычно сплошная среда принимается изотропной, т.е. предполагается, что свойства тела, выделенного из нее, не зависят от его ориентации в пределах этой среды. Материалы, имеющие различные свойства в разных направлениях, называют анизотропными (например, дерево, ткани (косой и кривой крой), армированная пластмасса, бетон). К анизотропным относятся и материалы с направленной кристаллизацией и с монокристаллической структурой. Отдельно взятый кристалл материала анизотропен, но т.к. в объеме реального тела содержится бесконечно большое количество хаотично расположенных кристаллов, принимается, что материал изотропен.

Металлы и сплавы, как правило, изотропны, так как большинство металлов имеет мелкозернистую структуру. Благодаря большому количеству кристаллов свойства материалов выравниваются в различных направлениях и можно считать эти материалы практически изотропными. В настоящее время широкое распространение получили анизотропные композиционные материалы, состоящие из двух компонентов – наполнителя и связующего. Наполнитель состоит из уложенных в определенном порядке высокопрочных нитей – матрицы, что и определяет значительную анизотропию композита. Композиционные материалы имеют высокую прочность при значительно меньшем, чем металлы весе. 

3. Принимается, что до определенной величины деформации материалов подчиняются закону Гука и весьма малы относительно размеров тела, поэтому все расчеты выполняются по исходной, т.е. недеформированной, схеме, к которой применим принцип независимости действия сил (принцип суперпозиции).

Результат воздействия на тело системы сил равен сумме результатов воздействия тех же сил, прилагаемых к телу последовательно и в любом порядке (рис. 1.9). Под словами «результат воздействия» следует понимать – деформации, внутренние силы и перемещения отдельных точек.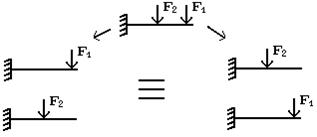



Рис. 19. Использование принципа суперпозиции
Должны соблюдаться два условия:

1. перемещения малы по сравнению с размерами тела,

2. перемещения линейно зависят от силы.

С помощью этого принципа сложный случай приводится к простым.

4. После снятия нагрузки геометрические размеры тела полностью или частично восстанавливаются. Свойство тела восстанавливать свои первоначальные размеры после разгрузки называется упругостью. При решении большинства задач в сопротивлении материалов принимается, что материал конструк­цийабсолютно упругий. Это допущение справедливо, пока нагрузки не превышают определенного значения. При больших нагрузках в элементах конструкций появляются пластические деформации. Пластичностьюназывается свойство тела сохранять после прекращения действия нагрузки, или частично полученную при нагружении, деформацию.

Ползучестьюназывается свойство тела увеличивать деформацию при постоянных внешних нагрузках.

5. Перемещения, возникающие под действием внешних сил в упругом теле, малы по сравнению с его размерами. Это допущение называетсяпринципом начальных размеров. В большинстве случаев механические конструкции работают в упругой зоне (в зоне действия закона Гука), а упругие деформации малы по сравнению с геометрическими размерами (рис. 1.10). Допущение позволяет при составлении уравнений равновесия пренебречь изменениями формы и размеров конструкции.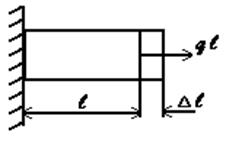 



∆l≪l

Рис. 1.10. Принцип неизменности геометрических размеров

 

6. Предполагается, что в сечениях, достаточно удаленных от мест приложения нагрузки, характер распределения напряжений не зависит от конкретного способа нагружения.  Основанием для такого утверждения служит принцип Сен-Венана, справедливый для любого типа напря­женного состояния и формулируемый следующим образом: особенности приложения внешних нагрузок проявляются, как правило, на расстояниях, не превышающих характерных размеров поперечного сечения стержня или другое определение: в точках тела, достаточно удаленных от мест приложения нагрузок, величина внутренних сил весьма мало зависит от конкретного способа приложения этих нагрузок, а зависит только от ее статического эквивалента (рис. 11). Этот принцип во многих случаях позволяет производить замену одной системы сил другой системой, статически эквивалентной, что позволяет часто значительно упростить расчет.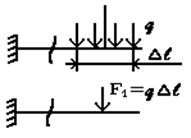



Рис. 1. 11. Использование принципа Сен-Венана
7. Принимается гипотеза плоских сечений(гипотеза Бернулли), 

введенной швейцарским ученым Д. Бернулли, гласящей, что плоские поперечные сечения стержня до деформации остаются плоскими и после деформации (рис.12).



Рис. 1.12. Гипотеза плоских  сечений

 

8. Считается, что ненагруженное тело свободно от каких бы то ни было внутренних сил любой природы. Изменению формы и размеров тела под нагрузкой сопротивляются силы взаимодействия между частицами материала, называемые силами упругости. В дальнейшем, говоря о внутренних силах, будем иметь в виду именно эти силы упругости, не принимая во внимание молекулярные силы, имеющиеся и в ненагруженном теле. Это допущение полностью не выполняется ни для одного материала. Причины возникновения неравномерных внутренних или начальных усилий:

- В стальных деталях из-за неравномерного остывания;

- В дереве из-за неравномерного высыхания;

- В бетоне в процессе твердения.

В тех случаях, когда есть основания предполагать, что эти силы значительны, стараются определить их экспериментально. Однако, часто они достаточно малы, чтобы их учитывать.

 Использование этих понятий и допущений существенно упрощает изучение поведения конструкций под нагрузкой, а соответствие условного материала реальным материалам достигается введением в расчет элементов сооружений экспериментально получаемых механических характеристик реальных материалов. 

3. 
   Напряжения
   

При определении внутренних силовых факторов их считают приложенными в центре тяжести сечения. В действительности внутренние силы, являясь результатом взаимодействия частиц тела, непрерывно распределены по сечению. Интенсивность этих сил в разных точках сечения может быть различной. При увеличении нагрузки на элемент конструкции увеличиваются внутренние силы и соответственно увеличивается их интенсивность во всех точках сечения. Если в некоторой точке интенсивность внутренних сил достигнет определенного для данного материала значения, в этой точке возникает трещина, развитие которой приведет к разрушению элемента, или возникнут недопустимые пластические деформации. Следовательно, о прочности элементов конструкций следует судить не по значению внутренних силовых факторов, а по их интенсивности. Меру интенсивности внутренних сил называют напряжением.

В окрестности произвольной точки, принадлежащей сечению некоторого нагруженного тела, выделим элементарную площадку  , в пределах которой действует внутреннее усилие ∆F (рис. 1.13, а).

Среднее значение интенсивности внутренних усилий на площадке, называемое средним напряжением, определяют по формуле



Уменьшая площадь ∆A, в пределе получаем истинное напряжение в данной точке сечения



Векторная величина p называется полным напряжением в точке. В международной системе единиц (СИ) за единицу напряжения принят паскаль (Па=Н/м²) – это напряжение, при котором на площадке 1 м² действует внутренняя сила 1 Н.

Так как эта единица очень мала, в расчетах используют кратную единицу напряжения – мегапаскаль (1 МПа=10⁶ Па).

Разложим вектор полного напряжения p на две составляющие (рис.1.13, б).

Проекция вектора полного напряжения p на нормаль к данной площадке обозначается через σ и называется нормальным напряжением.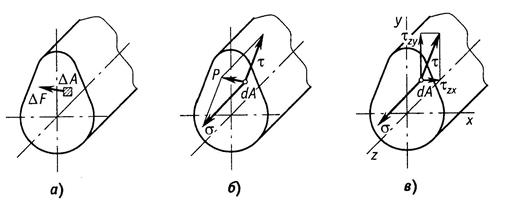



Рис. 1.13

 

Составляющую, лежащую в сечении в данной площадке обозначается через τ и называется касательным напряжением.

Нормальное напряжение, направленное от сечения, считают положительным, направленное к сечению – отрицательным.

Нормальные напряжения возникают, когда под действием внешних сил частицы, расположенные по обе стороны от сечения, стремятся удалиться одна от другой или сблизиться. Касательные напряжения возникают, когда частицы стремятся сдвинуться одна относительно другой в плоскости сечения.

Касательное напряжение можно разложить по координатным осям на две составляющие   и   (рис.1.13, в). Первый индекс при τ показывает, какая ось перпендикулярна сечению, второй – параллельно какой оси действует напряжение. Если в расчетах направление касательного напряжения не имеет значения, его обозначают без индексов. 

Между полным напряжением и его составляющими существует зависимость



Через точку тела можно провести бесконечное число сечений и для каждого из них напряжения имеют свое значение. Следовательно, при определении напряжений необходимо указывать положение не только точки тела, но и сечения, проведенного через эту точку.

Совокупность напряжений для множества элементарных площадок, проходящих через данную точку, образует напряженное состояние в этой точке.

В дифференциальные уравнения равновесия бесконечно малого прямоугольного параллелепипеда входят шесть независимых скалярных величин, соответствующих составляющим напряжений по его граням. Они определяют тензор напряжений:



При этом учитывается свойство парности касательных напряжений (τ_xy = τ_yx,  τ_xz = τ_zx,  τ_yz= τ_zy): на двух взаимно перпендикулярных площадках составляющие касательных напряжений, перпендикулярные к линии пересечения площадок, равны по величине и взаимно направлены либо к линии пересечения, либо от нее.

Если площадка dA совпадает с поверхностью тела, то составляющие напряжения трансформируются в составляющие внешних сил, действующих на поверхности тела. Соответствующие уравнения выражают условия на поверхности, или статические граничные условия.

Площадка, на которой касательные напряжения равны нулю, называется главной. Через точку проходят три главные площадки. По ним действуют главные напряжения, которые обозначаются σ₁, σ₂, σ₃ (σ_1≥σ₂ ≥σ₃).

Напряжения в поперечных сечениях связаны с внутренними силовыми факторами определенными зависимостями.

Возьмем в сечении бесконечно малую площадку площадью dA. По этой площадке в общем случае действуют бесконечно малые (элементарные) внутренние силы (рис. 1.14)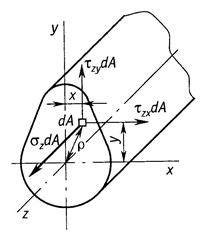





Рис. 1.14

 

Соответствующие элементарные моменты относительно координатных осей x, y, z имеют вид:



Просуммировав бесконечно малые силы и моменты, действующие в сечении, получим выражения, связывающие внутренние силовые факторы с напряжениями: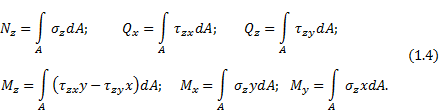



В соответствии с теоремой Вариньона, известной из теоретической механики, и зависимостью между напряжениями τ,   и  , выражение для   можно записать в виде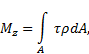



где



Интегральные зависимости (1.4) можно использовать для определения напряжений по найденным методом сечений внутренним силовым факторам при условии, что известны законы распределения напряжений по сечению. Поскольку эти законы зависят от вида деформации, то обратная задача (определение напряжений через внутренние усилия) решается путем совместного использования условий равновесия и условий деформирования тела. Задача становится статически неопределимой.

3. 
   Перемещения и деформации
   

Под действием внешних сил твердые тела изменяют свою геометрическую форму, то есть деформируются. Если в теоретической механике тела считаются абсолютно жесткими, то в сопротивлении материалов тела обладают способностью деформироваться, т.е. под действием внешней нагрузки изменять свои начальные размеры и форму. Точки тела при этом неодинаково перемещаются в пространстве. Вектор  , имеющий свое начало в точке А недеформированного состояния, а конец в т.  деформированного состояния, называется вектором полного перемещения т. А (рис. 15, а). Его проекции на оси xyz называются осевыми перемещениями и обозначаются u, v и w, соответственно.

Для того, чтобы охарактеризовать интенсивность изменения формы и размеров тела, рассмотрим точки А и В его недеформированного состояния, расположенные на расстоянии S друг от друга (рис. 15, б).           



Рис. 1.15

 

Пусть в результате изменения формы тела эти точки переместились в положение   и  , соответственно, а расстояние между ними увеличилось на величину S и составило S + S. Величина



называется линейной деформацией в точке А по направлению АВ. Если рассматривать деформации по направлениям координатных осей xyz, то в обозначения соответствующих проекций линейной деформации вводятся индексы  ,  ,  .

Линейные деформации  ,  ,   характеризуют изменения объема тела в процессе деформирования, а формоизменения тела  угловыми деформациями. Для их определения рассмотрим прямой угол, образованный в недеформированном состоянии двумя отрезками ОD и ОС (рис. 1.15, б). При действии внешних сил указанный угол DOC изменится и примет новое значение  . Величина



называется угловой деформацией, или сдвигом в точке О в плоскости СОD. Относительно координатных осей деформации сдвига обозначаются  ,  ,  .

Линейные и угловые деформации – величины безразмерные. Деформацию  ,  ,   часто называют относительной линейной деформацией, а  ,  ,   – относительным сдвигом.

Положительными принимают линей­ную деформацию, соответствующую растяжению, и деформацию сдвига, отвечающую уменьшению первона­чального угла пересечения отрезков. Полагая деформации малыми, мы можем в дальнейшем пренебрегать ими по сравнению с единицей, а также их высокими сте­пенями по сравнению с первой степенью.

Совокупность линейных и угловых деформаций по различным направлениям и плоскостям в данной точке образует деформированное состояние в точке. В слу­чае малых деформаций оно полностью определяется линейными де­формациями трех взаимно перпендикулярных линейных элементов тела, проходящих через данную точку, и тремя деформациями сдвига этих линейных элементов. Соответствующие шесть незави­симых скалярных величин определяют тензор деформаций:



Главные оси деформации – три взаимно перпендикулярные прямые, проходящие через данную точку тела и совпадающие по направлениям с такими тремя линейными элементами тела, которые остаются взаимно перпендикулярными и после деформации. Линейные деформации по направлениям этих осей называются главными деформациями и обозначаются ε₁, ε₂, ε₃ (ε₁≥ε₂≥ε₃).

Следует подчеркнуть, что в сопротивлении материалов слово деформация имеет данное выше строгое определение и выступает как количественная мера изменения геометрических размеров в окрестностях точки.

 

3. 
   Закон Гука и принцип независимости действия сил
   

Многочисленные экспериментальные наблюдения за поведением деформируемых тел показывают, что в определенных диапазонах перемещения точек тела пропорциональны действующим на него нагрузкам. Впервые указанная закономерность была высказана в 1776 году английским ученым Р.Гуком в формулировке «ut tensio sic vis»- «какого растяжение - такова и сила» и носит название закона Гука.

В соответствии с этим законом перемещение произвольно взятой точки А (рис. 15, а) нагруженного тела по некоторому направ­лению, например, по оси x, а может быть выражено следующим образом:



где Р - сила, под действием которой происходит перемещение u;  - коэффициент пропорциональности между силой и перемещением.

Очевидно, что коэффициент   зависит от физико-механических свойств материала, взаимного расположения точки А и точки  приложения и направления силы Р, а также от геометрических особенностей системы. Таким образом, последнее выражение следует рассматривать как закон Гука для данной системы.

В современной трактовке закон Гука определяет линейную зависимость между напряжениями и деформациями, а не между силой и перемещением.

Касательные напряжения τ вызывают угловые деформации γ, причем при малых деформациях они не влияют на изменение линейных размеров и, следовательно, на линейные деформации. Нормальное напряжение σ не влияет на угловые деформации, так как при этом изменяются только линейные размеры отрезков, а не углы между ними.

Параметры E и G, входящие в эти формулы, называют модулями упругости материала соответственно первого и второго рода. Они характеризуют его сопротивляемость деформированию, или жесткость в упругой стадии деформации. При одном и том же напряжении деформации больше у того материала, у которого меньше модуль упругости. Численные значения E и G для каждого конструктивного материала определяются экспериментально. Они имеют размерности напряжений. На практике удобно использовать единицы, кратные паскалю: мегапаскаль (1 МПа=10⁶ Па) и гигапаскаль (1 ГПа=10⁹ Па). 

При растяжении или сжатии одновременно с продольной деформацией ε =∆l/l (рис. 16, а), в элементе возникает поперечная деформация   = -∆а/а.

Отношение



называют коэффициентом Пуассона.

Величины коэффициента Пуассона и модуля упругости для различных материалов определяют опытным путем и их значения приведены в ГОСТ. Между модулем упругости и модулем сдвига существует зависимость



Установим связь между нормальными напряжениями и линейными деформациями, справедливые для любого напряженного состояния. Рассмотрим бесконечно малый элемент, имеющий форму кубика, на гранях которого возникают напряжения растяжения σ_x, σ_y, σ_z. При действии только напряжения σ_x, элемент получает продольную деформацию в направлении оси х, равную, согласно закону Гука, σ_x/Е (рис. 16,б). Одновременно его размеры вдоль осей y и z уменьшатся, при этом соответствующие поперечные деформации будут равны

Аналогичное действие оказывает растягивающие напряжения σ_y и σ_z.. Каждое из них вызывает продольную деформацию в своем направлении σ_у/Е и σ_z/Е и поперечные деформации по двум другим направлениям (рис. 16,в, г).



Суммируя деформации в направлениях каждой оси, получаем







Эти зависимости представляют собой математические выражения обобщенного закона Гука. Напряжения σ_x, σ_y, σ_z  следует подставлять в формулы со своим знаком.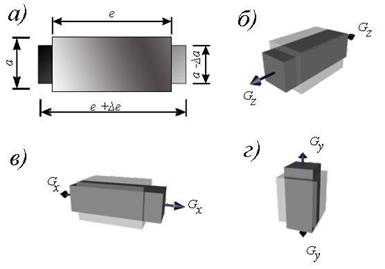



Рис. 1.16. Деформация элемента при растяжении:

а) общий вид элемента;  б) деформации в направлении осиz; 

в) то же оси x; г)  то же оси у

 

Системы, для которых соблюдается условие пропорциональности между напряжениями и деформациями, подчиняютсяпринципу суперпозиции, или принципунезависимости действия сил.

В соответствии с этим принципом перемещения и внутренние силы, возникающие в упругом теле, считаются независящими от порядка приложения внешних сил. То есть, если к системе приложено несколько сил, то можно определить внутренние силы, напряжения, перемещения и деформации от каждой силы в отдельности, а затем результат действия всех сил получить как сумму действий каждой силы в отдельности. Принцип независимости действия сил является одним из основных способов при решении большинства задач механики линейных систем.