Бродский А.К. Краткий курс общей экологии. Учебное пособие. Спб. Деан. 2000. 224 с
 Скачать 2.74 Mb.
|
|
Тема 7 ДИНАМИКА ЧИСЛЕННОСТИ ПОПУЛЯЦИЙ Объектом изучения демоэкологии, или популяционной экологии, служит популяция. Ее определяют как группу организмов одного вида (внутри которой особи могут обмениваться генетической информацией), занимающую конкретное пространство и функционирующую как часть биотического сообщества. Популяция характеризуется рядом признаков; единственным их носителем является группа, но не особи в этой группе. Важнейшее свойство популяции — плотность, т. е. число особей, отнесенное к некоторой единице пространства. 7.1. ЭКСПОНЕНЦИАЛЬНАЯ И ЛОГИСТИЧЕСКАЯ КРИВЫЕ РОСТА Численность популяции определяется в основном двумя противоположными явлениями — рождаемостью и смертностью. Пусть N — численность популяции. Тогда отношение dN/dtозначает мгновенную скорость измененияN, т. е. изменение N в момент времени t, а отношение dN/dtNудельную мгновенную скорость изменения численности популяции. Так, в популяции инфузорий с исходной численностью 100 особей и с численностью, равной 200 особей через час, рост популяции равен 100 особей в час, а рост популяции в расчете на одну особь равен 100/100-1 = 1 особь в час. Таким же способом определяют рождаемость и смертность. Если dN - число рожденных особей в популяции, то коэффициент рождаемости b = dN/dt, если dN— число погибших особей, то коэффициент смертности d = dN/dt. Разность r = b-dпредставляет собой коэффициент прироста изолированной популяции, в которой нет ни эмиграции, ни иммиграции. Коэффициент прироста популяции—не что иное, как врожденная (специфическая) скорость естественного увеличения популяции, называемая иногда мальтузианским параметром. Эта величина является мерой мгновенной удельной (в расчете на одну особь) 116 скорости изменения размера популяции и выражается как число особей, отнесенное к единице времени в расчете на одну особь. Различают максимальнуюмгновеннуюскоростьприроста популяции (rmax) и фактическуюскорость увеличения популяции ra=b-d. При воображаемых идеальных условиях, когда значение bмаксимально, a dминимально, га достигает наибольшей величины — rmax 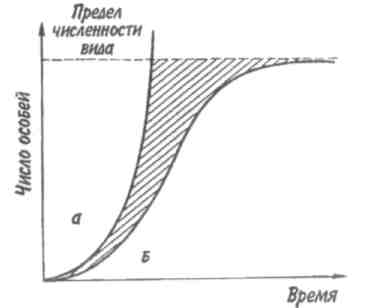 Рис. 7.1. Экспоненциальная (а) и логистическая (б) кривые роста популяции. Заштрихованная площадь — сопротивление среды. Если допустить, что коэффициент прироста имеет постоянную величину, то зависимость численности популяции от времени будет выражаться экспоненциальной кривой (рис. 7.1,а). Если r = const, то dN/dt = rN, следовательно, если N0—численность популяции в исходный момент, Nt—ее численность в момент t, то Nt = N0ert. Экспоненциальная кривая выражает так называемый биотическийпотенциал. В природе в основном наблюдается иная картина. Прежде всего коэффициент прироста не остается постоянным, так как рождаемость и смертность меняются в зависимости от условий среды и возраста организмов, а пища и территория редко предоставлены в достаточном объеме. Чаще всего реальный рост численности популяции выражается S-образной зависимостью, которую называют логистической кривой роста (рис. 7.1,6). Урав- 117 нение логистической кривой отличается от уравнения биотического потенциала корректирующим фактором: (K-N)/ К, где К—максимальное число особей, способных жить в рассматриваемой среде, т. е. асимптота кривой. Отсюда математическое выражение для логистической кривой имеет вид: dN/dt = rN[(K-N)K-1] или Nt = K/1+ea-rt, где a = r/ К. Пространство, заключенное между биотическим потенциалом и логистической кривой роста, представляет собой сопротивлениесреды. 7.2. СВОЙСТВА ПОПУЛЯЦИЙ От чего же зависят значения коэффициентов рождаемости и смертности? От очень многих факторов, действующих на популяцию извне, а также от собственных ее свойств. Объективный показатель способности организмов увеличивать свою численность — максимальная мгновенная скорость прироста популяции. Этот параметр обратно пропорционален продолжительности жизни организмов. В этом легко убедиться, обратившись к гиперболической зависимости между врожденной скоростью увеличения численности популяции и средним временем генерации, выраженным в днях (рис. 7.2). Мелкие орга-низмы имеют более высокие значения rmax, чем крупные, что объясняется меньшим временем генерации. Причина подобной корреляции понятна, поскольку организму для достижения крупных размеров требуется много времени. Отсрочка периода размножения также неизбежно ведет к уменьшению rmax. Тем не менее, преимущества, даваемые большими размерами тела, должны превышать недостатки, связанные с уменьшением rmax, так как в противном случае крупные организмы никогда не появились бы в эволюции. Тенденция к возрастанию размеров тела с течением геологического времени, прослеженная по ископаемым остаткам, послужила основанием для введения понятия увеличениефилетическогоразмера. Крупные размеры тела дают совершенно очевидные преимущества: более крупный организм должен привлекать мень- 118 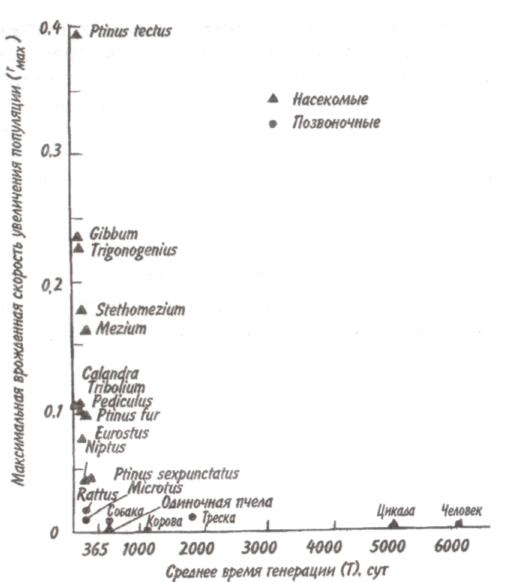 Рис. 7.2. Гиперболическая зависимость максимальной врожденной скорости увеличения популяции от времени генерации (по: Пианка, 1981). ше потенциальных хищников и, следовательно, он имеет больше шансов не стать жертвой и должен отличаться лучшей выживаемостью; мелкие организмы находятся в тесной зависимости от физической среды, даже очень слабые изменения которой могут оказаться для них губительными. Более крупные организмы легче переносят воздействие подобных изменений и соответственно лучше от них защищаются. Однако более крупным организмам требуется больше вещества и энергии в расчете на одну особь в единицу времени, чем мелким. Кроме того, для них существует гораздо меньше укрытий и безопасных мест. В жизни всех организмов в популяции можно выделить три основных периода: предрепродукционный, репродукционный и пострепродукционный. Относительная 119 продолжительность каждого из них у разных видов весьма различна. У многих животных первый период самый длинный. Ярким примером могут служить поденки, у которых предрепродукционный период достигает 3 лет, а репродукционный занимает всего от 2-3 ч до 1 сут. У американской цикады предрепродукционный период составляет 17 лет. Но есть виды, особи которых, едва появившись на свет, начинают интенсивно размножаться (большинство бактерий). Репродукционные возможности популяции зависят от ее возрастного состава. Продолжительность жизни особей популяции можно оценить, используя кривые выживания. Существует три типа кривых выживания (рис. 7.3). 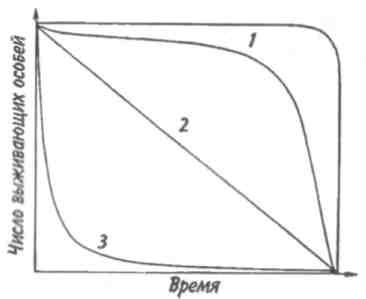 Рис. 7.3. Различные типы кривых выживания. 1 — дрозофила (верхняя кривая) и человек (нижняя), 2—пресноводная гидра, 3 —устрица. Первый тип (кривые 1) соответствует ситуации, когда большее число особей имеет одинаковую продолжительность жизни и умирает в течение очень короткого отрезка времени. Кривые характеризуются сильно выпуклой формой. Такие кривые выживания свойственны человеку (рис. 7.3, 1), причем кривая выживания для мужчин по сравнению с аналогичной кривой для женщин менее выпуклая, поэтому страховой полис для мужчин в большинстве стран Запада в 1,5 раза дороже, чем для 120
Среднийтиппирамидысоответствует равномерному распределению особей по возрастам в популяции со сбалансированными коэффициентами рождаемости и смертности — пирамида выравненная. Пирамида сузкимоснованием(обращенная), отвечающая популяции с численным преобладанием старых особей над молодняком, характерна для сокращающихся популяций. 121 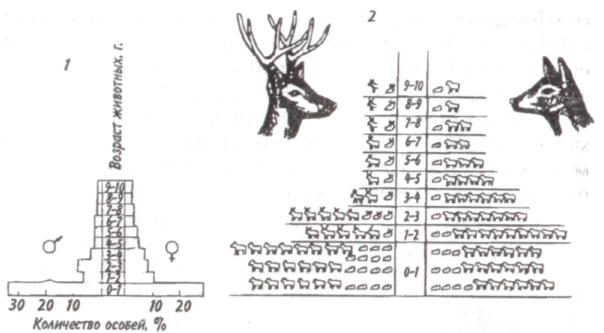 Рис. 7.5. Пирамида возрастов оленей Odocoileushemionus (из Рамада, 1981). 1 — классическое изображение, 2—более сложное изображение с учетом погибших особей в каждом классе, символически представленных силуэтами черепов. В таких популяциях коэффициент смертности превышает коэффициент рождаемости. Важным фактором изменения численности популяций явля- ется соотношение полов. Оно редко бывает равным единице, так как в большинстве случаев один из полов преобладает над другим. У позвоночных часто при рождении самцов бывает несколько больше, чем самок. У утиных самцы тоже нередко численно превалируют над самками. Зато в крупных популяциях белок Sciuruscarolinensisи S. nigerдоминируют самки. Большое значение для увеличения численности популяции имеют затраты на потомство, выражающиеся в определенной тактике размножения. Не все потомки равноценны: те из них, которые произведены на свет в конце вегетационного сезона, обычно имеют меньшую вероятность дожить до взрослого состояния по сравнению с потомками, появившимися на свет раньше. Сколько усилий должны родители затрачивать на каждого потомка? При постоянной величине репродуктивного усилия средняя приспособленность отдельного потомка связана обратным соотношением с их числом. Один 122    крайний вариант тактики размножения — вложить все в единственного очень крупного и хорошо приспособленного потомка, другой —максимально увеличить общее число произведенных на свет потомков, вложив в каждую особь как можно меньше. Однако наилучшая тактика размножения —это компромисс между производством максимально большого числа потомков и образованием потомства максимально высокой приспособленности.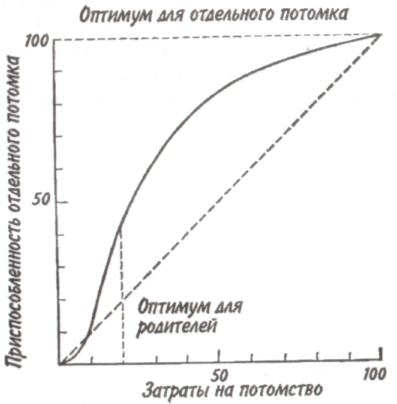 Рис. 7.6. Зависимость количества и качества потомства от репродуктивного усилия родителей (по: Пианка, 1981). Объяснения в тексте. Указанное соотношение количества и качества потомства иллюстрирует простая графическая модель (рис. 7.6). В маловероятном случае, т. е. в случае линейной зависимости приспособленности потомков от затрат на них родителей, приспособленность каждого отдельного потомка уменьшается с увеличением размера помета или кладки. Так как приспособленность родителей или, что то же самое, общая приспособленность всех по- 123 томков — постоянная величина, с точки зрения родителей не существует оптимального размера кладки. Однако поскольку первоначальные расходы на потомство вносят больший вклад в приспособленность потомков, чем последующие (имеет место S-образный характер зависимости приспособленности потомков при увеличении вклада родителей; см. рис. 7.6), то очевидно, что существует некоторый оптимальный размер кладки. В данном гипотетическом случае родители, расходующие только 20% своего репродуктивного усилия на каждого из пяти своих потомков, получат большую отдачу от своего вклада, чем при любом другом размере кладки. Подобная тактика, будучи оптимальной для родителей, не является наилучшей для каждого отдельно взятого потомка, максимальная приспособленность которого достигается в том случае, если он единственный отпрыск, получивший полный вклад усилий от своих родителей. Следовательно, в данном случае налицо «конфликт родителей и детей». Особенно большое влияние на форму S-образной кривой оказывает конкурентная обстановка. В сильно разреженной среде (конкурентный вакуум) наилучшей репродуктивной стратегией следует считать максимальный вклад вещества и энергии в размножение для продуцирования как можно большего количества потомков в самые короткие сроки. Поскольку конкуренция невелика, потомки могут выжить, даже если они имеют очень малые размеры и низкую приспособленность. Однако в насыщенной среде обитания, где заметно проявляются эффекты массы, а конкуренция остра, оптимальной стратегией будет расходование большого количества энергии на преодоление конкуренции, повышение собственной выживаемости и на продуцирование более конкурентоспособных потомков. При подобной стратегии лучше иметь крупных потомков, а поскольку энергетически они дороже, их может быть произведено на свет меньше. Итак, свойства популяции можно оценить по таким показателям, как рождаемость, смертность, возрастная структура, соотношение полов, частота генов, генетическое разнообразие, скорость и форма кривой роста и т. д. 124 Плотность популяции определяется ее внутренними свойствами, а также зависит от факторов, действующих на популяцию извне. 7.3. КОЛЕБАНИЯ ЧИСЛЕННОСТИ ПОПУЛЯЦИЙ Когда популяция прекращает расти, ее плотность обнаруживает тенденцию к флуктуациям относительно верхнего асимптотического уровня роста. Такие флуктуации могут возникать либо в результате изменений физической среды, вследствие чего повышается или снижается верхний предел численности, либо в результате внутри-популяционных взаимодействий, либо, наконец, в результате взаимодействия с соседними популяциями. После того, как верхний предел численности популяции (К) окажется достигнутым, плотность может некоторое время оставаться на этом уровне или сразу резко упасть (рис. 7.7, кривая 1). Это падение окажется еще резче, если сопротивление среды увеличивается не постепенно, по мере роста популяции, а проявляется внезапно (кривая 2). В таком случае популяция будет реализовы- 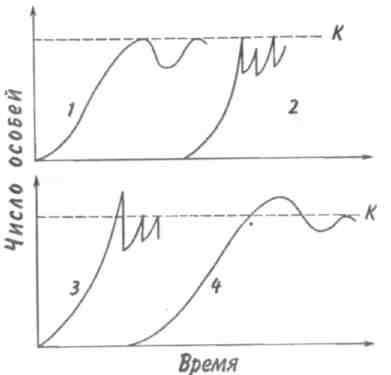 Рис. 7.7. Различные типы флуктуации плотности популяции. Объяснения в тексте. 125 вать биотический потенциал. Однако экспоненциальный рост не может происходить долго. Когда экспонента достигает парадоксальной точки стремления к бесконечности, как правило, происходит качественный скачок — быстрое увеличение численности сменяется массовым отмиранием клеток или гибелью особей. Пример подобных флуктуации — вспышка размножения насекомых, сменяемая массовой их гибелью; размножение и гибель водорослей («цветение» водоемов). Возможна и такая ситуация, при которой численность популяции «перескакивает» через предельный уровень (кривые 3, 4), если питательные вещества и другие необходимые для жизни факторы накоплены еще до начала роста популяции. Этим, в частности, можно объяснить, почему новые пруды и озера часто богаче рыбой, чем старые. Существует два основных типа колебаний численности популяций (рис. 7.8). При первом типе периодические нарушения среды, такие как пожары, наводнения, ураганы и засухи, часто приводят к катастрофической, не зависящей от плотности, смертности. Так, численность популяции однолетних растений и насекомых обычно быстро растет весной и летом, а с наступлением холодной погоды резко сокращается. Популяции, рост которых дает регулярные или случайные всплески, называ- 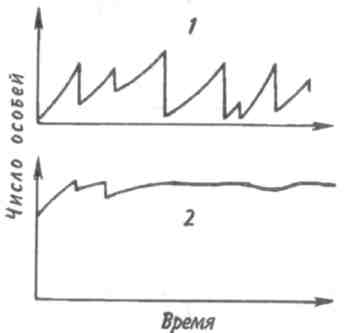 Рис. 7.8. Флуктуация плотности популяции у оппортунистических (1) и равновесных (2) видов. 126   ются оппортунистическими(рис. 7.8,1). Другие популяции, так называемые равновесные(свойственные многим позвоночным), обычно находятся в состоянии, близком к состоянию равновесия с ресурсами, а значения их плотности гораздо более устойчивы (рис. 7.8,2).Два выделенных типа популяций представляют собой только крайние точки континуума, однако при сравнении разных популяций подобное разделение часто оказывается полезным. Значение противопоставления оппортунистических популяций равновесным заключается в том, что действующие на них независящие и зависящие от плотности факторы, так же как совершающиеся при этом события, по-разному влияют на естественный отбор и на сами популяции. Мак-Артур и Уилсон (1967) назвали эти противоположные типы отбора г-отбором и К-отбором в соответствии с двумя параметрами логистического уравнения. Некоторые характерные признаки г- и К-отбора приведены в таблице. Во временном отношении колебания численности популяции бывают непериодическимии периодическими. Последние можно разделить на колебания с периодом в несколько лет и сезонные колебания. Непериодические флуктуации носят непредвиденный характер. В Тихом океане, особенно в районе Большого барьерного рифа к северо-востоку от Австралии, с 1966 г. наблюдается увеличение численности морской звезды Терновый венец, Acanthasterplanci. Терновый венец, будучи ранее малочисленным (менее одной особи на 1 м2), достиг к началу 1970-х годов плотности 1 особь на 1 м2. Морская звезда приносит большой вред коралловым рифам, так как питается полипами, составляющими их живую часть. Она «очистила» 40-километровую полосу рифов у острова Гуам менее чем за три года. Ни одна из гипотез, предложенных для объяснения внезапного увеличения численности морской звезды (исчезновение одного из ее врагов — брюхоногого моллюска Тритоний рог, Charoniatritonis, которого добывают из-за раковин, содержащих перламутр; увеличение содержания в морской воде ДДТ и в связи с этим нарушение естественного равновесия; влияние радиоактивных осадков), не может считаться удовлетворительной. 127 Пример периодических колебаний численности с периодом в несколько лет дают популяции некоторых арктических млекопитающих и птиц. У зайца-беляка и рыси период колебаний численности равен 9,6 года (рис. 7.9). Как видно из рисунка, максимум численности зайца по |
