Инвестиции - Колтынюк Б.А.. Удк 336 ббк 65. 26 К 61
 Скачать 24.66 Mb. Скачать 24.66 Mb.
|
Приложение 1. Примеры и задачи1. Дисконтирование 1.1. Дисконтирование денежных поступлений одного года Дисконтирование — это приведение разновременных показателей к какому-либо одному моменту времени — точке приведения. Существует несколько методов дисконтирования. Все они основаны на допущении, что деньги, которые должны быть получены (или израсходованы) в будущем, будут иметь меньшую ценность, чем в текущий момент. Предположим, что у нас скопилась некоторая сумма денег, которую мы решили поместить в банк. Нам предлагают, к примеру, вместо 240 тыс. руб., вложенных сегодня, через год вернуть 300 тыс. руб. Иначе говоря, 300 тыс. через год и 240 тыс. сейчас для нас эквивалентны: Коэффициент А — это пропорция между инвестируемой в текущий момент суммой и той суммой, которую нам через год предстоит получить в банке. В рассматриваемом случае: Как мы видим, коэффициент А < 1 уменьшает (дисконтирует) ожидаемую в будущем сумму до размеров той суммы, от которой мы отказываемся в настоящем. Коэффициент А принято называть коэффициентом дисконтирования, а процесс вычисления суммы, от которой нужно отказаться сейчас ради получения известной суммы в будущем, именуется дисконтированием. Коэффициент дисконтирования всегда меньше 1, поскольку в ином случае деньги сегодня стоили бы много меньше чем завтра. В общем виде: где PV — стоимость будущих поступлений в настоящее время, или текущая стоимость (англ. presentvalue); С1 — поступления будущего года (англ. cash flow). Из формулы (П.1.1) следует: Это выражение позволяет определить текущую стоимость будущих поступлений. Разница между поступающей в будущем и дисконтированной к настоящему времени стоимостью составляет доход. В нашем примере он равен 60 тыс. руб. Если соотнести между собой доход, получаемый через год, с размером средств, которые необходимо инвестировать в настоящее время, то можно определить доходность (ставку доходности) такой операции: Отсюда можно заключить: где Е — ставка доходности. В результате некоторых преобразований формулы (П. 1.3) получаем: или Тогда откуда Здесь t — номер шага расчета, t = 0, 1, 2, 3,..., Т, где Т — горизонт расчета. Если же норма доходности (дисконта) меняется во времени и на t-мшаге расчета достигает Et, то А0 = 1 и Аt = 1/РV( 1 + E) при t >0. Таким образом, коэффициент дисконтирования зависит от того (обратно пропорционален тому), какой годовой доходности ожидает инвестор от вложения своих сбережений. Для закрепления полученных знаний предлагаем решить следующие задачи. Задача 1. Определите доходность ваших вложений, если вы вложили 150 (200, 400, 600) тыс. руб., а через год получили соответственно 200 (300, 600, 900) тыс. руб. Оцените какую сумму выгоднее вкладывать. Задача 2. Определите, каковы должны быть поступления через год, если при ставке доходности 10 (20, 30, 40, 50, 60, 70, 80, 90, 100) % годовых вы вложили соответственно 200 (300, 400, 500, 600, 700, 800, 900, 1000, 1100) тыс. руб. Задача 3. Определите, какова должна быть текущая стоимость будущих поступлений, чтобы через год при ставке доходности 10 (20,30,40,50, 60, 70, 80, 90, 100) % годовых получить соответственно 100 (300, 400, 500, 600, 700, 800, 900, 1000, 1200) тыс. руб. Задача 4. Определите доходность на основании условий задач 2 и 3 при С1 = 1000 (10000, 12000, 12000, 14000, 15 000) и PV = 800 (7000, 8000,9000, 7000, 8000), 1.2. Дисконтирование денежных поступлений разных лет Известно, что любое отчуждение денежных средств приносит инвестору неудобства, обусловленные отказом от возможности лучшего вложения средств. Поэтому инвестор вряд ли согласится вкладывать средства более чем на год по ставке доходности, принятой при вложениях на год. Он потребует компенсации за все дополнительные неудобства. Эта компенсация может состоять не только в повышении ставки доходности, но и в сокращении объема вложения денежных средств в начальном периоде. По-видимому, такую компенсацию инвестор получит, вкладывая меньшую сумму, чем та, которая была бы помещена сроком на один год. Обозначим поступления второго года (начиная отсчет с текущего момента) через С2, коэффициент дисконтирования этой суммы — через А2, а искомый объем инвестиций — через PV2. Тогда: PV = А2 ∙С2. Предположим, что мы собираемся получить от данной операции доход 25 % годовых за каждый из предстоящих до выплаты двух лет. Задача решается поэтапно. Поступающая через два года сумма в 125 тыс. руб. будет «стоить» за год до этого (т. е. через год от настоящего момента): Это значит, что на следующий год следовало бы инвестировать 100 тыс. руб. для того, чтобы спустя год после этого (т. е. через два года от настоящего момента) получить 125 тыс. руб. Возникает вопрос: какую сумму надо инвестировать сейчас, чтобы на следующий год получить эти 100 тыс. руб., которые будут инвестированы для получения 125 тыс. руб. через два года? Ответ таков: Обобщая сказанное, запишем: В рассматриваемом примере: Коэффициент дисконтирования равен: В более общем виде (для любого числа лет между датой инвестирования и датой выплаты причитающейся суммы) формула выглядит так: где п — число лет между датой инвестирования и датой выплаты причитающейся суммы; Сп - сумма, причитающаяся к выплате через п лет; Еп—доходность инвестирования в течение п лет; PVn - современная дисконтированная стоимость денежной суммы, учитывающая все неудобства в течение п лет; Аn—коэффициент дисконтирования денежных поступлений, приходящийся на n-й год. Коэффициент дисконтирования сумм n-го года равен при этом: Для закрепления материала решите нижеследующие задачи. Задача 1. Сколько денег надо инвестировать сейчас, чтобы через 3 (5, 8, 10) лет получить соответственно при доходности 30 (40, 50, 60) % годовых 3 (6, 7, 8) млн руб.? Задача 2. Сколько денег получит вкладчик по истечении 3 (5, 8, 10) лет, если он сегодня вложил соответственно под 60 (70,80,90) % годовых 1 (2,3, 4) млн руб.? Задача 3. Определите фактическую и ожидаемую доходность от инвестирования одной и той же суммы на разные сроки (см. условие задачи 2), если банк уменьшил ставку доходности на 20 %. (Здесь необходимо отметить, что ожидание той или иной доходности в первую очередь может быть обусловлено темпами инфляции, политикой Центробанка, спросом на деньги.) 1.3. Расчет текущей стоимости с многоразовых поступлений от инвестиций Представим себе следующую ситуацию: имеется некий инвестиционный проект, который требует в первый период времени (год) вложения 125 млн руб., во второй — 150 млн руб., в третий — 160 млн руб. При этом ставки доходности соответственно составляют 25,30 и 40 % годовых. Какую сумму можно инвестировать сейчас в указанный инвестиционный проект? Задача решается по частям, исходя из требований инвестирования и с учетом ставок доходности: 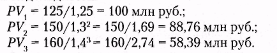 Сложив эти три значения, получим сумму, которую нужно вложить сейчас: В обобщенном виде формула выглядит так: 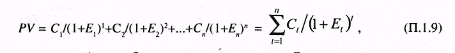 где t—номер года, t = 1,..., n; Ct—- поступления t-гo года; Et — доходность t-гогода. Для закрепления материала предлагаем на основе условий, представленных в табл.П. 1.1. определить сумму вложений в проекты в настоящее время. |
