|
|
Экономическая теория. Г.М.Гукасьян, и др.. Удк330 ббк 65. 01 Г93 Серия Высшее экономическое образование Об
8.3. РАСШИРЕНИЕ ПРОИ3ВОДСТВА
Расширение производства возможно различными путями. При сохранении неизменной технической базы увеличить выпуск можно за счет увеличения применения всех видов ресурсов. В этом
212
Глава 8. Производство предложение благ
случае имеет место увеличение масштабов производства, для его анализа используется понятие отдача от масштаба. В коротком периоде можно увеличить объем применения лишь переменного ресурса. В этом случае имеет место изменение пропорций, в которых применяются производственные ресурсы. Расширение нроизводства в коротком периоде исследуется с помощью понятия убывающей отдачи (или убывающей производителъности) переменного ресурса или, как иногда говорят, закона изменяющихся пропорций. Возможно также расширение производства за счет изменения его технической базы, то есть научно-технического прогресса
8.3.1. Отдача от масштаба.
Длительный период
Если выбран технически эффективный метод производства, то увеличение выпуска возможно за счет пропорционального увеличения использования всех производственных ресурсов. Это и есть изменение масштаба производства.
Пусть первоначальное соотношение между выпуском и применяемыми ресурсами описывается производственной функцией
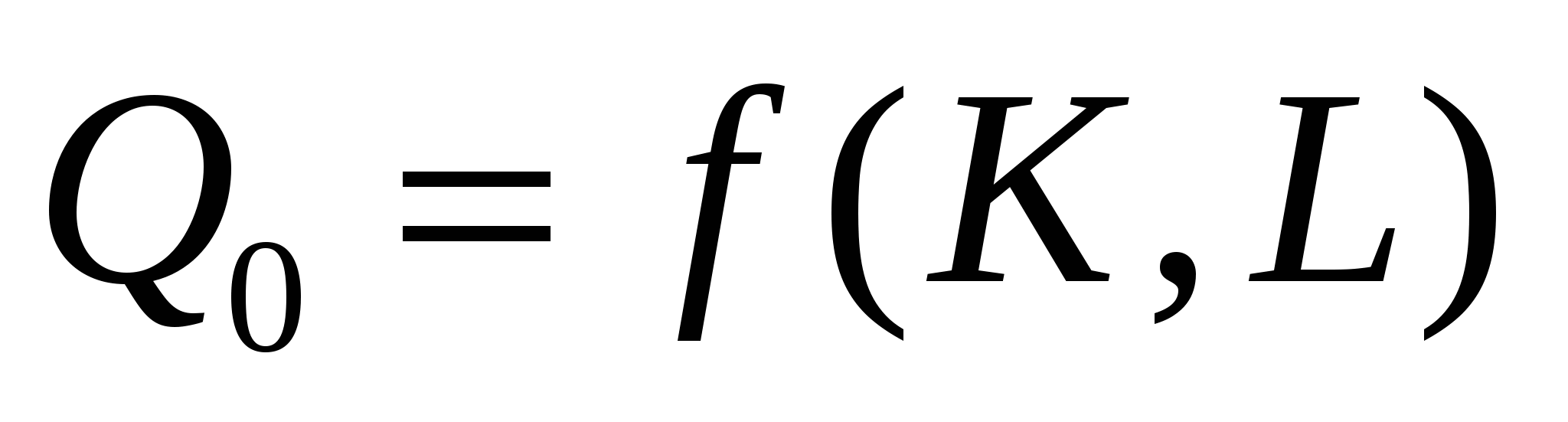
Если мы увеличим объемы применяемых ресурсов (масштаб производства) в kраз, то новый объем выпуска составит:
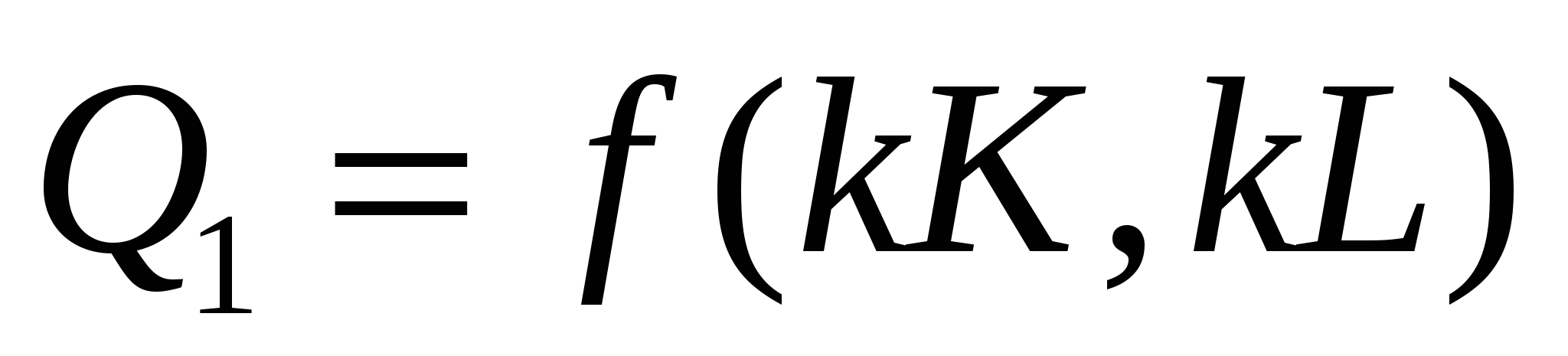
Если в результате выпуск увеличится также в kраз (Q1= kQ0),то имеет место постоянная отдача от масштаба (рис. 8.3, а).
Если выпуск увеличится менее, чем в kраз (Q,l. < k Q0), то имеет место убывающая отдача от масштаба (рис.
.3, б).
Если выпуск увеличится более, чем в kраз (QI> Q0),- имеет место возрастающая отдача от масштаба (рис. 8.3, в).
Введем еще одну характеристику производственной функции - однородность. Производственная функция называется однородной, если при увеличении количества всех производственных ресурсов в kраз, выпуск увеличивается в kt раз, так что
 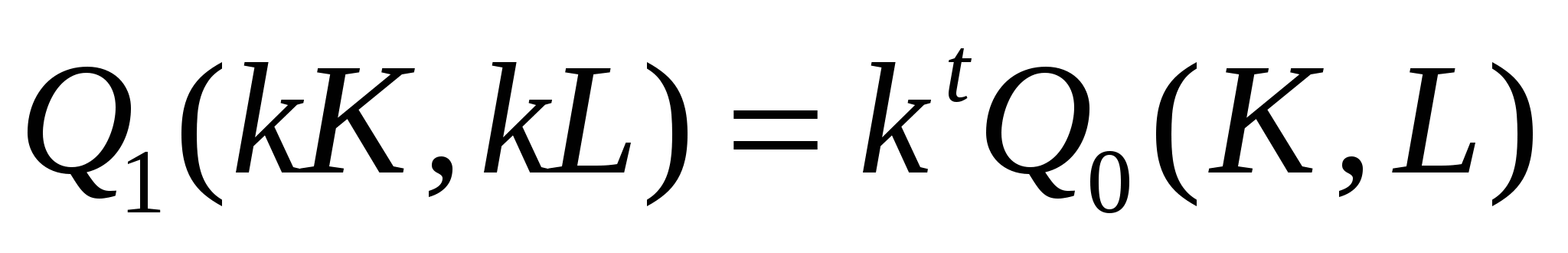 (8.5) (8.5)
Показатель t характеризует степень однородности функции. Если же равенство (8.5) для данной производственной функции не выполняется, то такая производственная функция называется неоднородноЙ.
213
Часть II. Микроэкономика
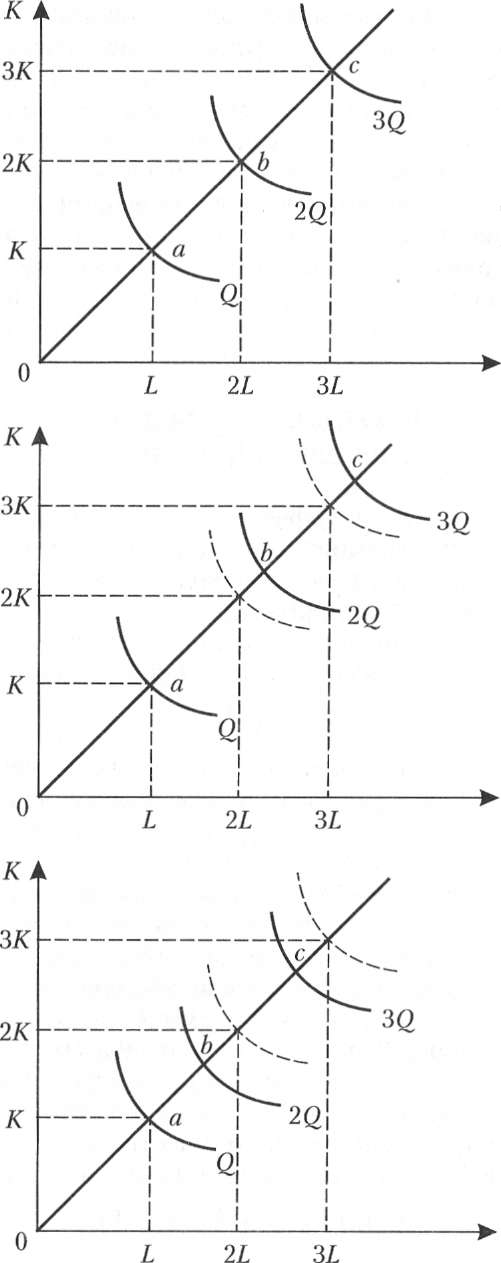
Рис. 83. Соотношение между объемом выпуска и количеством применяемых ресурсов. Отдача от масштаба
214
Глава 8. Производство предложение благ
Степень однородности может использоваться для характеристики типа отдачи от масштаба. Если t = 1 - отдача от масштаба постоянна, если t < 1, имеет место убывающая отдача от масштаба, если же t > 1 - возрастающая отдача от масштаба.
Для однородной производственной функции отдача от масштаба может быть представлена графически. Показателем отдачи может служить расстояние вдоль луча, проведенного из начала координат между изоквантами, представляющими кратные Q объемы выпуска - Q, 2Q,3Q и т. д. (рис. 8.3). В случае неоднородности производственной функции оценка отдачи от масштаба и ее графическое отображение могут представить значительные трудности.
Причины возникновения возрастающей отдачи от масштаба:
специализация и разделение труда;
использование более крупного и более эффективного обо-
рудования;
наличие сложных комплексных систем производства;
многономенклатурное производство;
финансовые выгоды крупномасштабных организаций и т.д.
Постоянная отдача от масштаба наблюдается в тех производствах, где ресурсы однородны (в техническом смысле) и их количества можно изменять пропорционально. В таких производствах увеличение выпуска может быть достигнуто путем кратного увеличения объема применения всех производственных ресурсов. Убывающая отдача, как правило, связана с ограниченными возможностями управления крупным производством. Концентрация управления (на неизменной технической базе) сверх определенного предела ведет к нарушению координации потоков ресурсы - выпуск.
Причинами отрицательной отдачи от масштаба также моеут быть: недостатки менеджера, слабая мотивация труда рабoчиx, сложность агрегатно-поточной организации производства и т. д.
Во многих случаях характер отдачи от масштаба изменяется при достижении определенных пределов выпуска. До определенных пределов рост производства может сопровождаться постоянной и даже возрастающей отдачей от масштаба, которая затем сменяется убывающей.
Лучи, проведенные из начала координат на рис. 8.3, называют линиями роста. Они характеризуют технически возможные пути расширения производства, то есть переход с более низкой на более высокую изокванту.
215
Э
Часть II. Микроэкономика
Среди возможных линий роста представляют интерес изоклинали, вдоль которых предельная норма технического замещения ресурсов при любом объеме выпуска постоянна.
8.3.2. Убывающая отдача переменного ресурса.
Короткий период
В коротком периоде в отличие от длительного часть ресурсов остается неизменной, тогда как другая часть может быть увеличена. Поэтому для короткого периода линия роста может быть представлена не лучом, проведенным из начала координат, а прямой, параллельной оси переменного фактора. Очевидно, что соотношение К/Lвдоль такой линии уменьшается, поскольку фиксированное количество К приходится на все большее количество L. Таким образом, в коротком периоде рост выпуска происходит при изменяющихся пропорциях между постоянным и переменным ресурсом.
При этом увеличение количества переменного ресурса рано или поздно приведет к сокращению предельного и среднего продукта этого ресурса. Если бы этого не произошло, можно было бы, например, увеличивая количество удобрений, достигнуть такой урожайности, что весь мировой урожай мог бы собираться на участке земли, не превышающем по площади размеров цветочной клумбы.
Действие закона изменяющихся пропорций иллюстрирует рис. 8.4.
При постоянной отдаче от масштаба, как мы знаем, удвоение обоих факторов ведет и к удвоению объема выпуска. На рис. 8.4 а точка b на изоклинали ОАлежит на изокванте, соответствующей удвоенному выпуску 2Q. Если же постоянный ресурс будет зафиксирован в объеме, а объем переменного ресурса L будет увеличен вдвое, мы достигнем лишь точки С, лежащей на более низкой изокванте, чем 2Q. Для достижения же выпуска 2Q нам потребуется увеличить использование переменного ресурса L до L·, то есть увеличить его количество более, чем в два раза. Следовательно, увеличение переменного ресурса при фиксированном объеме постоянного характеризуется убывающей производительностью.
Очевидно, что в случае убывающей отдачи от масштаба (рис. 8.4, б) удвоение переменного ресурса дает еще меньший относительный прирост выпуска, чем при постоянной отдаче. При возрастающей отдаче от масштаба (рис. 8.4, в) производительность переменного фактора также падает.
216
Глава 8. Производство предложение благ
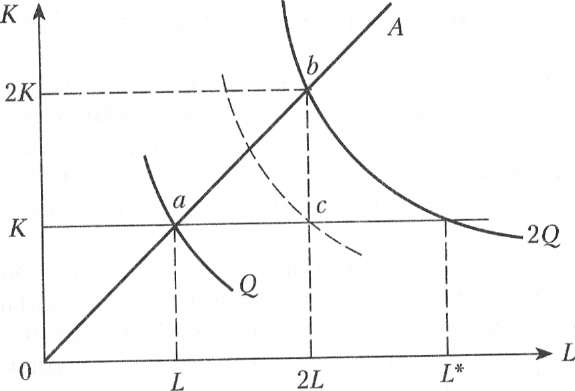
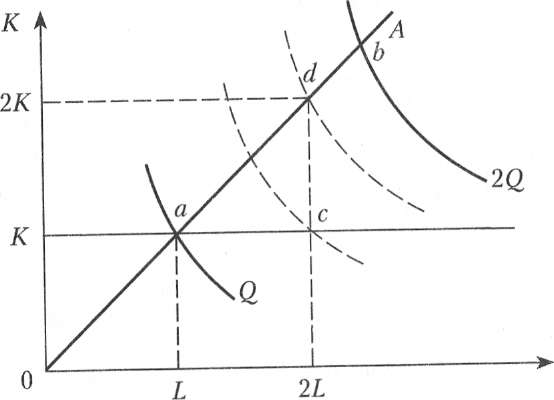
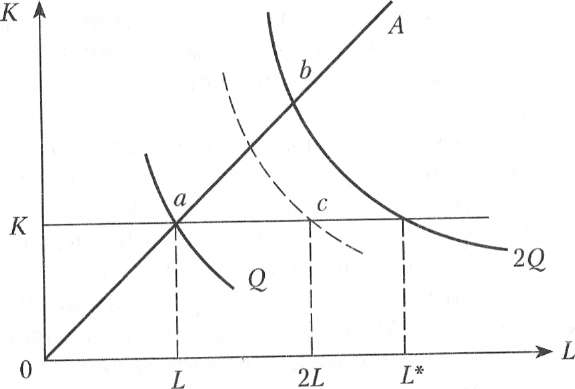
Рис. 8.4. Отдача от масштаба в коротком периоде
217
Часть II. Микроэкономика
8.3.3. Производственная функция и технический прогресс
Рост производства возможен, наконец, за счет техничеекого прогресса, который заключается в появлении новых, тех:iшчески более эффективных способов производства. Эти новые способы должны быть учтены в производственной функции, тогда как ставшие технически неэффективными способы должны быть исключены из нее.
Графически технический прогресс может быть отображен сдвигом вниз изокванты, характеризующей определенный объем выпуска и, возможно, изменением ее конфигурации. На рис. 8.5 изокванта Q1 характеризует тот же объем выпуска, что и изокванта Q0. Но теперь этот объем может быть произведен с использованием меньших количеств ресурсов К и L.
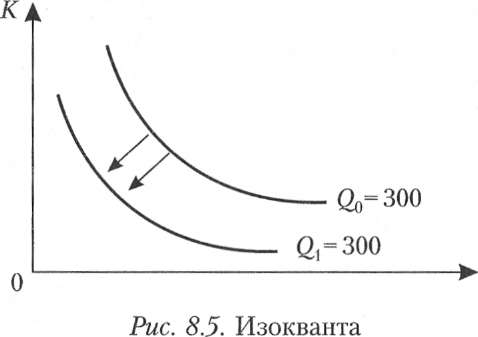
Сдвиг изокванты может сопровождаться изменением ее конфигурации, что означает изменение в соотношениях применяемых ресурсов. Обычно в связи с этим различают три типа технического прогресса: капиталоинтенсивный, трудоинтенсивный и нейтральный.
Технический прогресс называется капиталоинтенсивным (трудосберегающим), если предельная норма технического замещения (MRTSLK)снижается. Это значит, что технический прогресс сопровождается опережающим увеличением предельного продукта капитала по сравнению с предельным продуктом труда.
Технический прогресс называется трудоинтенсивным (капиталосберегающим), если MRTSLKвозрастает. Технический прогресс сопровождается опережающим увеличением предельного продукта труда по сравнению с предельным продуктом капитала.
При нейтральном техническом прогрессе MRTSLКостается неизменной.
218
Глава 8. Производство предложение благ
8.4. ОПТИМАЛЬНАЯ КОМБИНАЦИЯ РЕСУРСОВ И ОПТИМАЛЬНЫЙ ПУТЬ РОСТА
8.4.1. Равновесие производителя
Анализ с помощью изоквант имеет для производителя очевидные недостатки, так как использует только натуральные показатели затрат ресурсов и выпуска продукции. В теории произнодства равновесие производителя определяется симметричным равенством предельной нормы технического замещения ресурсов K и L соотношению их цен. Если обозначить цену услуг капитала (арендную плату за час работы оборудования) через r , а цену услуг труда (часовую ставку заработной платы) через w, то условие равновесия (оптимума) производителя можно записать в виде (Q = const):
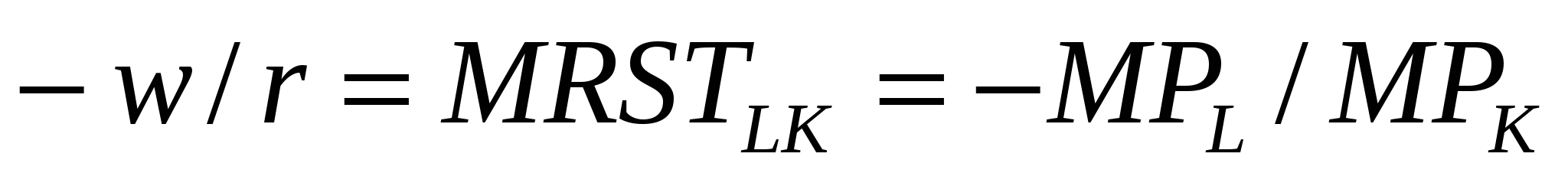 (8.6) (8.6)
Если бы эти соотношения не были равны, например, MPL/w > МРК/ r, было бы возможно использовать больший объем труда по отношению к капиталу, но в этом случае будет действовать яакон убывающей отдачи, и MPLбудет снижаться. Аналогичным образом до тех пор, пока на единицу труда будет использоваться больший объем капитала, МРкбудет повышаться. Данная закономерность будет действовать до тех пор, пока не выполнится условие (8.6). В этом случае фирма откажется от стратегии замещения труда капиталом.
Роль бюджетной прямой в теории производства выполняет линия равных затрат - изокоста, представляющая множество всех комбинаций ресурсов, которые могли бы быть приобретены предприятием при определенной сумме денежных расходов. Обозначим сумму возможных расходов предприятия через С, получим бюджетное ограничение
C=rхK +wxL, (8.7)
откуда легко определить уравнение изо кос ты:
К = C/r- (w/r)xL. (8.8)
Соотношение цен факторов w/r, как очевидно, характеризует наклон изокосты.
Рост бюджета производителя или пропорциональное снижение цен ресурсов сдвигает изокосту вправо, а сокращение бюджета или рост цен - влево (рис. 8.6).
Оптимальная комбинация ресурсов представлена на рис. 8.7.
219
Часть II. Микроэкономика
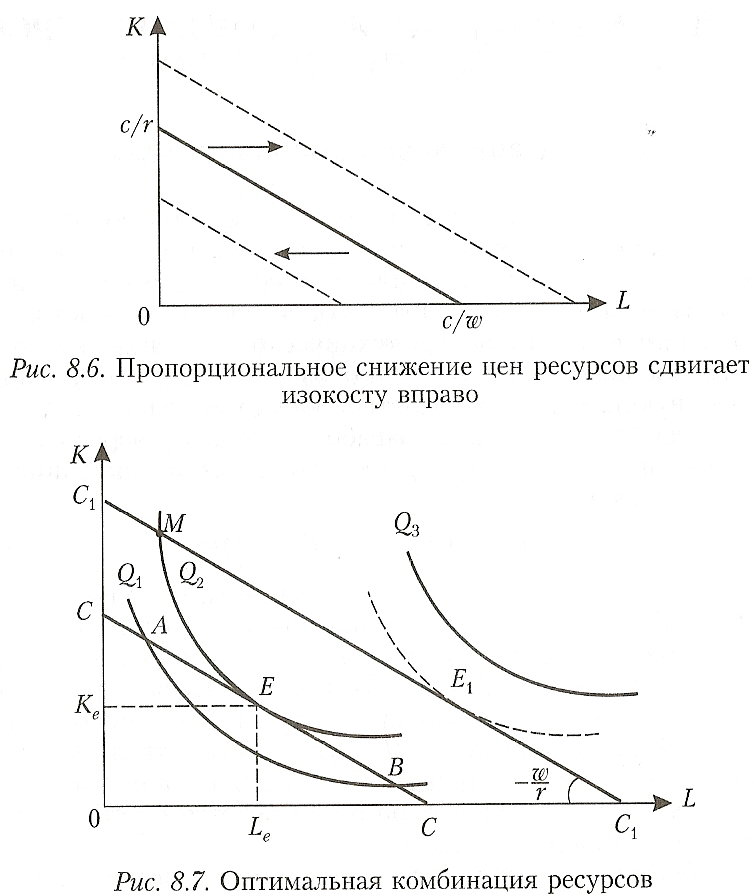
Комбинации ресурсов А, Е, В лежат на одной и той же изокосте СС и, значит, обойдутся при данных ценах ресурсов предприятию в одну и ту же сумму С. Но комбинация Е является наиболее предпочтительной из них, поскольку принадлежит наиболее высокой из всех достижимых при данном уровне затрат
изокванте Q2. .
Комбинация ресурсов Еобеспечит, таким образом, и наибольший выпуск по сравнению с любой другой комбинацией ресурсов, имеющей равную стоимость.
Комбинация ресурсов М технически столь же эффективна, как и комбинация Е. Но при данных ценах ресурсов (мы полагаем пока цены ресурсов неизменными) комбинация М экономически неэффективна. Ведь за ту же сумму средств С1 С1 предприятие может приобрести комбинацию ресурсов Е1 позволяющую получить больший объем продукции.
220
Глава 8. Производство предложение благ
8.4.2. Оптимальный путь роста
Предположим, что цены ресурсов остаются неизменными, тогда как бюджет предприятия постоянно растет. Соединив точки касания изоквант с изокостами, мы получим линию ОС – «путь развития» (путь роста). Эта линия показывает темпы роста соотношения между факторами в процессе расширения производства (рис. 8.8) .
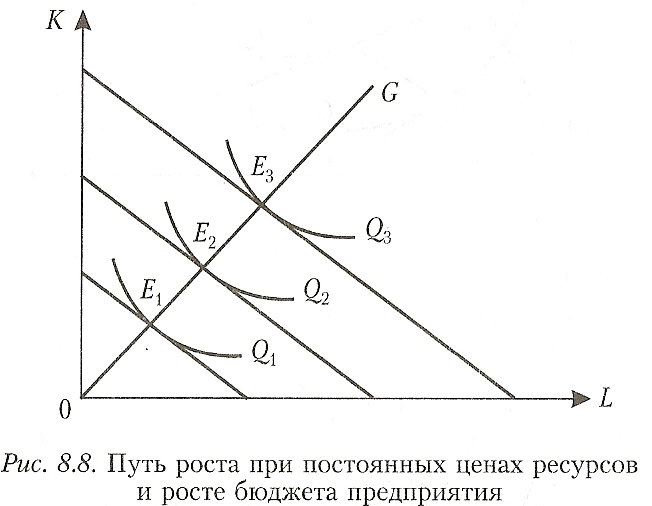
В длительном периоде все производственные ресурсы переменны, и поэтому здесь в принципе не существует предела расширению производства.
Задача предприятия в этом случае сводится к задаче выбора оптимального пути роста. При данной производственной функции и данных ценах ресурсов оптимальный путь роста определяется множеством точек касания соответствующих изоквант и изокост.
Если производственная функция однородна, оптимальный путь роста определяется лучом, выходящим из начала координат, наклон которого определяет оптимальное соотношение K/L и зависит от соотнщпения цен ресурсов (рис. 8.9).
На рис. 8.9, а при соотношении цен w/r оптимальный путь роста определяется лучом ОА, а при соотношении цен w1/r1- лучом ОВ. Понятно, что при изменении соотношения цен произойдет и изменение оптимального пути роста.
В коротком периоде (рис. 8.9, б) количество ресурса Кфиксировано на уровне К и предприятие может расширять произ-
221
Часть II. Микроэкономика
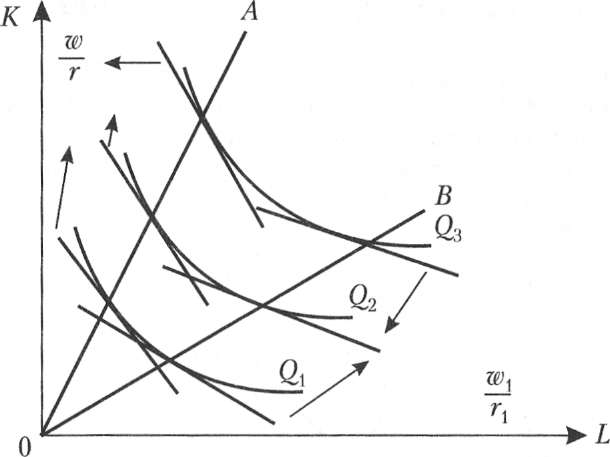
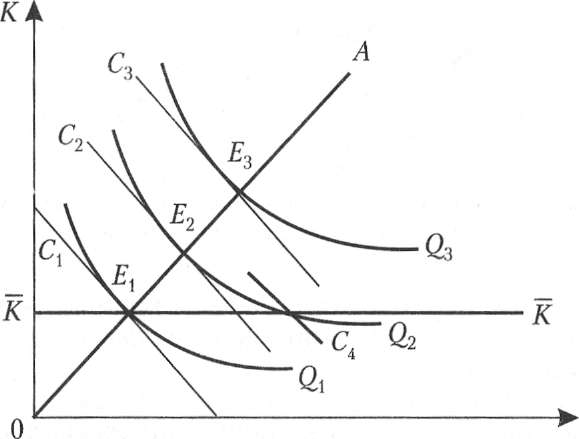
Рис. 8.9. Оптимальный путь роста
водство лишь за счет увеличения количества переменного ресурса, то есть вдоль линии КК, параллельной оси L. При данных ценах ресурсов их оптимальная комбинация недостижима. В самом деле, оптимальным путем роста было бы движение вдоль луча ОА. Однако при фиксированном количестве постоянного фактора Кточки Е2И Езнедостижимы, а рост производства возможен лишь вдоль линии КК. Очевидно, что при данных ценах увеличение выпуска в коротком периоде потребует более высоких затрат (изокоста С4 расположена дальше от начала координат, чем изокоста С2 при том же объеме выпуска Q2).
222
Глава 8. Производство предложение благ
8.5. ФУНКЦИЯ И ЭЛАСТИЧНОСТЬ ПРЕДЛОЖЕНИЯ
Функцией предложения называют зависимость объема предложения от определяющих его факторов:
QSA= f (РA, РB…,Pz, R, К, C, X…),
где QSA- объем предложения товара А в единицу времени; РA, РB…,Pz - цены данного и остальных товаров; R- наличие производственных ресурсов; К - характер применяемой технологии; С - налоги и дотации; Х- природно-климатические условия.
Зависимость между ценой блага и максимальным объемом его предложения при прочих неизменных условиях называется функцией предложения по цене: Qs= f(Р). Графически это представлено на рис. 8.10.
Движение вдоль кривой предложения означает изменение объема предложения: чем выше цена, тем выше (при прочих равных условиях) объем предложения и, наоборот, чем ниже цена, тем ниже объем предложения.
Сдвиг кривой предложения влево или вправо отражает изменение предложения: оно происходит под влиянием изменения всех факторов, определяющих функцию предложения, кроме цены данного товара. |
|
|
 Скачать 9.75 Mb.
Скачать 9.75 Mb.