цос. Умноженной на множитель в форме показательной функции W
 Скачать 6.33 Mb. Скачать 6.33 Mb.
|
|
2. Свойство симметрии. Если периодическая последовательность xp(n) с периодом в N отсчетов является действительной, то ее ДПФ Xp(k) удовлетворяет следующим условиям симметрии Re[Xp(k)]=Re[Xp(N-k)] Im[Xp(k)]=-Im[Xp(N-k)] | Xp(k)|=| Xp(N-k)| arg Xp(k)=-arg Xp(N-k) Аналогичные равенства справедливы и для конечной последовательности x(n), имеющей N-точечное ДПФ X(k). 3.Сдвиг по времени: циклический сдвиг сигнала на отсчетов приводит к повороту фазового спектра, в то время как амплитудный спектр не меняется. 4.Сдвиг по частоте: Пусть Произведем циклический сдвиг спектра 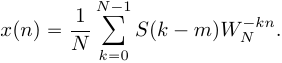 (19) Введем замену переменной 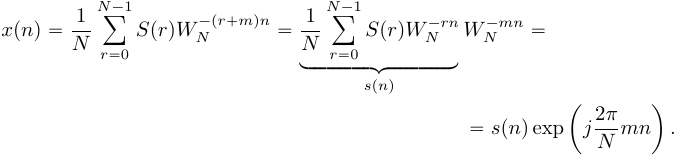 (20) Таким образом, циклический частотный сдвиг ДПФ осуществляется умножением сигнала на комплексную экспоненту. Важно отметить, что после умножения на комплексную экспоненту вещественного сигнала, результирующий сигнал будет комплексным, а его спектр перестанет быть симметричным. 5.Произведение последовательностей Пусть сигнал Тогда ДПФ сигнала 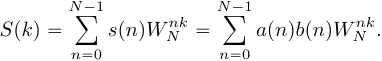 (16) Подставим в (16) 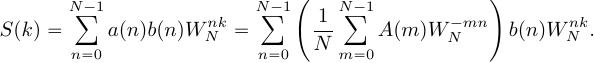 (17) Поменяем местами операции суммирования в выражении (17) и получим: 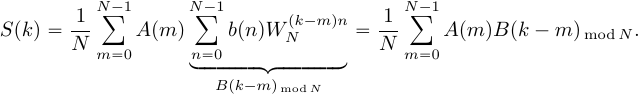 (18) Таким образом, ДПФ произведения сигналов представляет собой циклическую свертку ДПФ этих сигналов. Цикличность свертки также объясняется периодичностью спектров ДПФ. Именно по этому был добавлен индекс взятия сдвинутого спектрального отсчета 6.Циклическая свертка Пусть сигнал 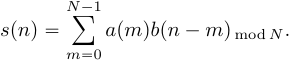 (13) Рассчитаем ДПФ сигнала 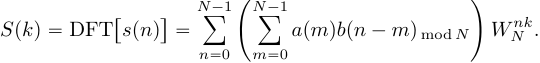 (14) Поменяем местами операции суммирования: 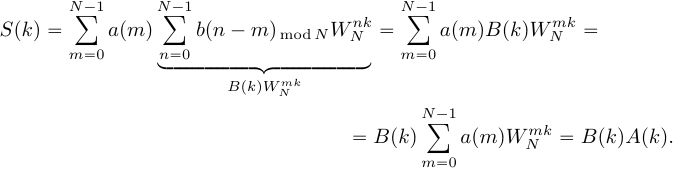 (15) При выводе выражения (15) было использовано свойство циклического временного сдвига. Таким образом, ДПФ циклической свертки двух сигналов равен произведению ДПФ этих сигналов. Это свойство позволяет использовать алгоритмы быстрого преобразования Фурье для вычисления сверток сигналов.
Разделение исходной последовательности прореживанием по времени Прореживание по времени заключается в разделении исходной последовательности Последовательность Прореживание по времени для 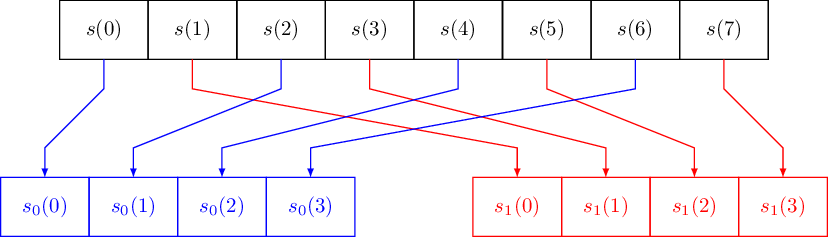 Рисунок 1. Прореживание по времени для Процедура объединения ДПФ, окончательно можно записать процедуру объединения как: 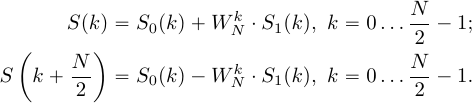 (12) Граф <<бабочка>> Выражение (12) объединяет два 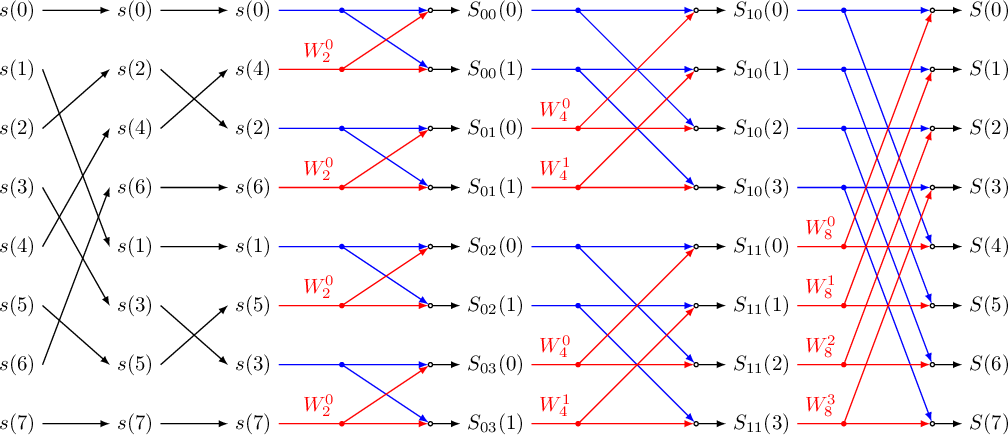 Рисунок 4. Граф алгоритма БПФ с прореживанием по времени для На первом этапе отсчеты входного сигнала переставляются местами и исходная последовательность делится на «четную» и «нечетную» последовательности. Потом «четная» и «нечетная» последовательности в свою очередь делятся на «четную» и «нечетную» последовательности. Данная процедура называется двоично-инверсной перестановкой, так можно выполнить перенумерацию отсчетов, переписав номер отсчета в двоичной системе счисления в обратном направлении. Например, По аналогичному правилу поменяются местами все отсчеты, при этом некоторые останутся на месте, в частности Важно отметить, что данный метод перенумерации должен применяться при записи числа в двоичной системе, состоящей из разрядов. В приведенном примере После двоично-инверсной перестановки получаем четыре 2-точечных ДПФ: 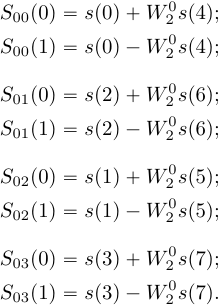 (13) (13)На основе четырех 2-точечных ДПФ формируются два 4-точечных ДПФ: 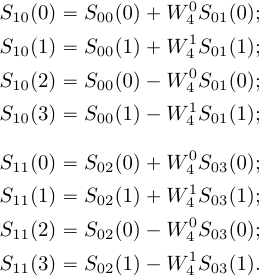 (14) (14)И на последнем уровне формируется полное ДПФ входного сигнала: 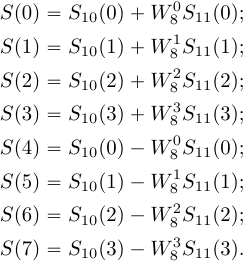
Интеграл свертки. Рассмотрим процесс в цепи при действии на ее входе сигнала произвольной формы f1(t) (рис. 1). Этот сигнал можно представить в виде последовательности прямоугольных импульсов длительностью Δx с амплитудами f1(kΔx). 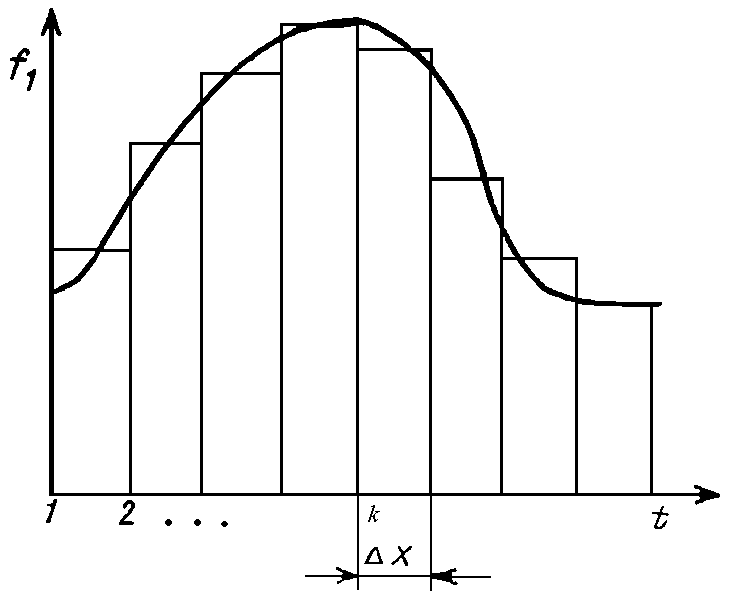 Рис. 1 При малых значениях Δx каждый такой импульс эквивалентен действию на цепь δ-импульса, включаемого в момент t = kΔx и имеющего площадь f1(kΔx) Δx. Поэтому входной сигнал представим в виде суммы 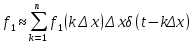 . После перехода к пределу при Δx → 0, kΔx → x получим . После перехода к пределу при Δx → 0, kΔx → x получим 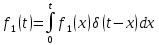 . .Поскольку реакция цепи на каждый δ-импульс описывается импульсной характеристикой hδ, то для выходной величины f2(t) можно записать аналогичный интеграл, в котором реакция на входной импульс δ(t – x) выражена как hδ (t – x): 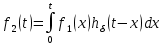 Полученный интеграл называется интегралом свертки и используется при вычислении реакции цепи f2(t) на воздействие f1(t) произвольной формы. Он и является основой временнóго метода расчета переходных процессов. Указанные выше пределы интегрирования требуют уточнения, особенно, при наличии в подынтегральных сомножителях слагаемых в виде δ-функций. При вычислении интеграла свертки необходимо учитывать, что первый сомножитель под интегралом f1(x) = 0 при x < – 0; соответственно hδ (t – x) = 0 при t – x < – 0, то есть при x > t + 0. Именно эти значения пределов интегрирования (– 0 < x<t < + 0) необходимо рассматривать при вычислении. При ограниченном значении f1 δ-слагаемое может содержаться в hδ (t – x). Вклад этого слагаемого можно учесть отдельно. Для этого запишем 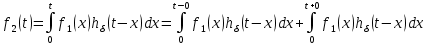 Так как второй интеграл можно преобразовать к виду , 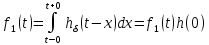 то окончательно получим то окончательно получим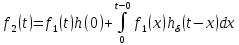 В последнем выражении под интегралом учитывается только ограниченная часть импульсной характеристики hδ. Дискретная свертка. При больших длинах ядра свертки сигналов существует специальный алгоритм, позволяющий вычислить ее значительно быстрее. Этот алгоритм основан на следующей важной теореме. Теорема свертки: свертка во временной области эквивалентна умножению в частотной области; умножение во временной области эквивалентно свертке в частотной области. Утверждение теоремы означает, что для выполнения свертки двух сигналов можно перевести их в частотную область, перемножить их спектры и перевести результат обратно во временную область. Такая операция выглядит громоздко. Однако с появлением алгоритмов БПФ, позволяющих быстро вычислять преобразования Фурье, вычисление свертки через частотную область резко сокращает число операций и поэтому стало широко использоваться в теории связи. При значительных длинах ядра свертки такой подход позволяет в сотни раз сократить время вычисления свертки. По аналогии со сверткой двух непрерывных сигналов u(t) и h(t) в системах цифровой обработки вводят линейную дискретную свертку, представляющую собой вещественный дискретный сигнал, отсчеты которого связаны с отсчетами двух вещественных дискретных сигналов {г/Д и [hj соотношением В т.е. можно переставлять местами исходный сигнал и ядро свертки. Связь с преобразованиями Фурье Дискретный сигнал skможно записать в виде суммы весовых импульсов Кронекера: sk = s(kΔt) = 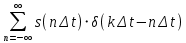 {\displaystyle s_k = s (k \Delta t) = \sum_{n= -\infty}^{\infty} s(n \Delta t) \cdot \delta (k \Delta t - n \Delta t)\,\!} {\displaystyle s_k = s (k \Delta t) = \sum_{n= -\infty}^{\infty} s(n \Delta t) \cdot \delta (k \Delta t - n \Delta t)\,\!}Тогда спектр сигнала по теореме запаздывания: s(ω) = 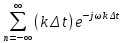 {\displaystyle s_k = s (k \Delta t) = \sum_{n= -\infty}^{\infty} s(n \Delta t) \cdot \delta (k \Delta t - n \Delta t)\,\!} {\displaystyle s_k = s (k \Delta t) = \sum_{n= -\infty}^{\infty} s(n \Delta t) \cdot \delta (k \Delta t - n \Delta t)\,\!}{\displaystyle s(\omega) = \sum_{n= -\infty}^{\infty} s(k \Delta t) e^{-j \omega k \Delta t} \,\!} После замены z=e−jωΔt{\displaystyle z = e^{-j \omega \Delta t} \,\!} получится: S(ω) = 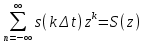 {\displaystyle S(\omega) = \sum_{n= -\infty}^{\infty} s(k \Delta t) z^k = S(z) \,\!} {\displaystyle S(\omega) = \sum_{n= -\infty}^{\infty} s(k \Delta t) z^k = S(z) \,\!}Отсюда следует, что дискретное преобразование Фурье является частным случаем z-преобразования при z=e−jωΔt.{\displaystyle z = e^{-j \omega \Delta t} \,\!.} Аналогичной подстановкой z=e−p{\displaystyle z = e^{-p} \,\!} может осуществляться переход к дискретному преобразованию Лапласа. В общем виде: S(ω) = S(z), z = e−jωΔt, S(p) = S(z), z=e−pΔt (1.2){\displaystyle S(\omega) = S(z), z = e^{-j \omega \Delta t}, S(p) = S(z), z = e^{-p \Delta t} \qquad \color{Maroon}(1.2) \,\!} Обратное преобразование: S(z) = S(ω),ω= 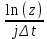 , S(z) = S(p), p = , S(z) = S(p), p = 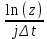 (1.3){\displaystyle S(z) = S(\omega), \omega = \frac{\ln z}{ j \Delta t}, S(z) = S(p), p = \frac{\ln z}{\Delta t} \qquad \color{Maroon}(1.3) \,\!} (1.3){\displaystyle S(z) = S(\omega), \omega = \frac{\ln z}{ j \Delta t}, S(z) = S(p), p = \frac{\ln z}{\Delta t} \qquad \color{Maroon}(1.3) \,\!}При отрицательной символике z связь между представлениями осуществляется соответственно подстановками z−1=ejωΔt{\displaystyle z^{-1} = e^{j \omega \Delta t} \,\!} и z−1=ep.{\displaystyle z^{-1} = e^{p} \,\!.} При zk=ejωkΔt{\displaystyle z^{k} = e^{j \omega k \Delta t} \,\!} z-преобразование представляет собой особую форму представления дискретных сигналов, при которой на полином S(z){\displaystyle S(z) \,\!} можно ссылаться как на временную функцию (по значениям коэффициентов kΔt{\displaystyle k \Delta t \,\!}), так и на функцию частотного спектра сигнала (по значениям аргумента ω{\displaystyle \omega \,\!}). Использование для вычисления реакции линейной цепи с постоянными параметрами Временной метод (метод интеграла положения, метод интеграла Дюамеля) основывается на представлении входного сигнала цепи в виде суммы элементарных сигналов вида единичного скачка или очень короткого импульса ( δ – функции). Тогда, зная отклик линейной цепи на каждый элементарный сигнал и суммируя их можно получить в соответствии с принципом суперпозиции (наложения) полный отклик цепи на входной сигнал сложной формы. Выберем в качестве элементарного сигнала δ – функцию. Тогда входной сигнал в соответствии с (1.19) можно записать следующим образом Очевидно, выходной сигнал Так как оператор Wц не зависит от времени, его можно внести под знак интеграла. Тогда Если момент появления входного сигнала t0=0, то с учётом того, что выходной сигнал не может появиться ранее входного, выражение (5.23) принимает вид Таким образом, сигнал на выходе линейной цепи представляет собой свёртку входного сигнала с импульсной характеристикой цепи. Линейная цепь с постоянными параметрами при преобразовании проводит операцию взвешенного суммирования всех мгновенных значений входного сигнала, начиная с момента t0=0 и заканчивая текущим моментом времени t. Роль весовой функции выполняет импульсная характеристика цепи. |
