цос. Умноженной на множитель в форме показательной функции W
 Скачать 6.33 Mb. Скачать 6.33 Mb.
|
|
Порядок КИХ-фильтра всегда на 1 меньше длины его ИХ. Передаточная функция КИХ-фильтра: 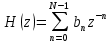 , где , где 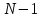 – порядок КИХ-фильтра, b – отсчёты ИХ. – порядок КИХ-фильтра, b – отсчёты ИХ.Иначе порядок КИХ фильтра можно определить как максимальную по модулю степень при 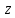 внутри передаточной функции. внутри передаточной функции.В случае БИХ-фильтра порядок определяется как наибольшая степень числителя либо знаменателя его передаточной функции. Передаточная функция БИХ-фильтра: 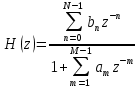 , где , где 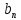 , , 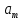 – коэффициенты ИХ. – коэффициенты ИХ.Структура ЦФ отображает алгоритм вычисления реакции по разностному уравнению и определяется видом передаточной функции. На рисунке 19.5 приведены структуры КИХ-фильтров с ЛФЧХ с симметричной (а) и антисимметричной (б) ИХ. В случае (а) можно увидеть, что одинаковые коэффициенты 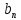 имеют первый и последний, второй и предпоследний и т.д. выходы линий задержки. Если подать на такой фильтр единичный импульс, то на выходе получим симметричную ИХ: имеют первый и последний, второй и предпоследний и т.д. выходы линий задержки. Если подать на такой фильтр единичный импульс, то на выходе получим симметричную ИХ: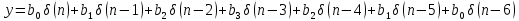 В случае (б) коэффициент 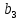 будет равен нулю, т.к. длина ИХ нечётна, а реакция будет равна: будет равен нулю, т.к. длина ИХ нечётна, а реакция будет равна: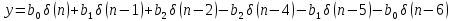 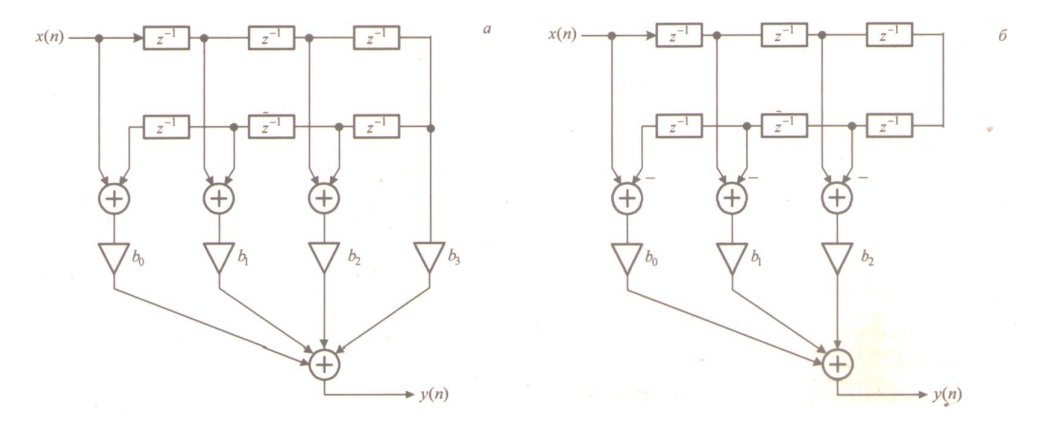 Рис. 19.5 – Структуры КИХ-фильтров с ЛФЧХ с симметричной и антисимметричной ИХ. Процедура синтеза КИХ-фильтра методом окон является итерационной и включает в себя следующие шаги: Задание требований к АЧХ Оценка порядка фильтра R и выбор окна Оценкой порядка R называют начальное значение порядка в итерационной процедуре синтеза фильтра. Окном называют весовую функцию 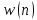 – вещественную неотрицательную последовательность длины – вещественную неотрицательную последовательность длины 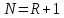 , максимальную в центре и монотонно спадающую к границам. , максимальную в центре и монотонно спадающую к границам.Расчёт ИХ идеального фильтра 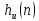 , симметрично усечённой до длины N = R +1 (выделенной окном Дирихле) , симметрично усечённой до длины N = R +1 (выделенной окном Дирихле)ИХ может быть только симметричной и рассчитывается по известным аналитическим формулам для идеальных ФНЧ, ФВЧ, ПФ, РФ. Обязательным параметром усечённой ИХ является частота разрыва (отсечки), на которой нормированная АЧХ равна 0.5. Расчёт симметричной ИХ реального фильтра через сглаживание: 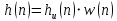 Проверка выполнения требований к АЧХ Проверка заключается в сравнении фактических максимальных по модулю отклонений АЧХ от идеальной АЧХ в ПП и ПЗ с заданными максимально допустимыми отклонениями. Возможны две ситуации: Требования к АЧХ не выполняются. В этом случае следует увеличить порядок R и вернуться к пп. 3–5. Требования к АЧХ выполняются. В этом случае следует уменьшить порядок R и вернуться к пп. 3–5. В обоих случаях увеличение/уменьшение порядка R продолжается до тех пор, пока не будет найден минимальный порядок, при котором выполняются требования к АЧХ. Выбор структуры КИХ-фильтра Синтез КИХ-фильтра методом частотной выборки. Как известно, синтез КИХ-фильтра сводится к нахождению импульсной характеристики исходя из АЧХ и ФЧХ. Идеальную импульсную характеристику можно найти через обратное преобразование Фурье над комплексной передаточной функцией идеального фильтра: 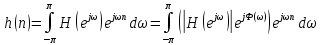 Однако на практике АЧХ может быть не задана аналитически, а если и задана, то аналитическое интегрирование не всегда возможно. На практике ИХ рассчитывается численно с помощью ОДПФ. Для вычисления ИХ необходимо продискретизировать комплексную передаточную функцию. Дискретизация производится на равноотстоящей сетке частот 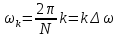 : :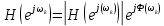 Тогда ИХ примет вид: 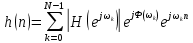 При дискретизации важно правильно продискретизировать ФЧХ: 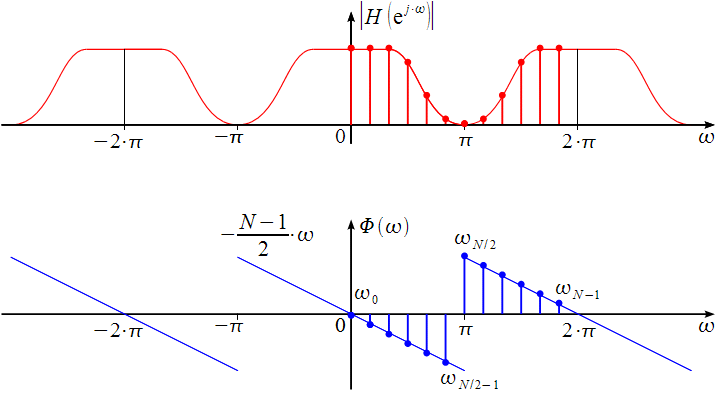 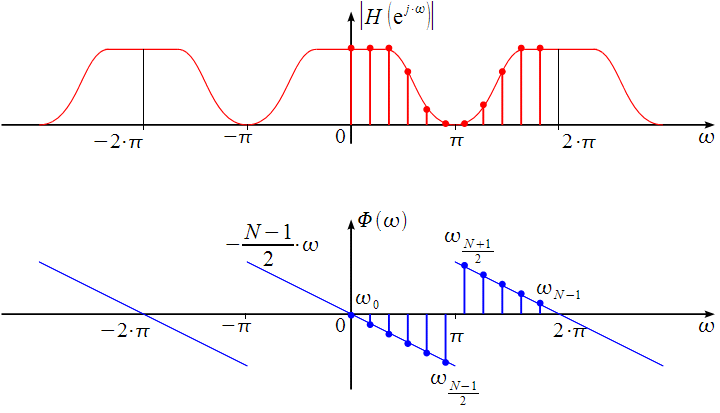 Рис. 19.6 – Дискретные АЧХ и ФЧХ при чётном (слева) и нечётном (справа) N Пример. Пусть 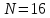 и необходимо синтезировать ФНЧ с частотой среза и необходимо синтезировать ФНЧ с частотой среза 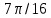 . .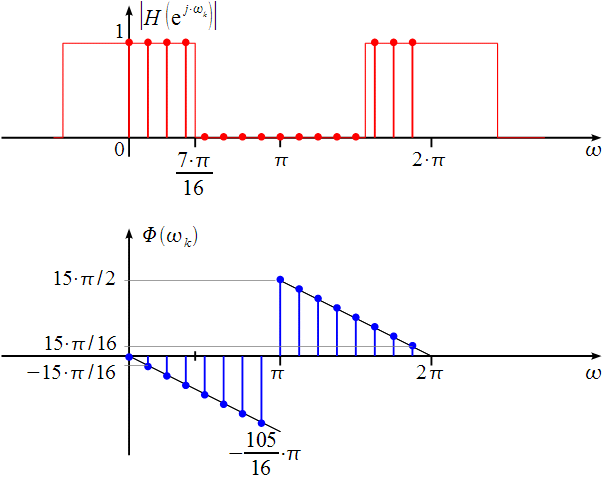 Рис. 19.7 – Дискретные ФЧХ и АЧХ фильтра Применив ОДПФ над комплексной функцией передачи получим ИХ: 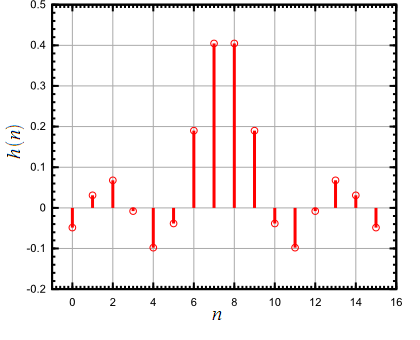 Рис. 19.8 – ИХ КИХ-фильтра с ЛФЧХ Построив АЧХ, непрерывную в области частот, можно заметить, что она проходит через выбранные дискретные отсчёты АЧХ, но отклоняется от АЧХ идеального ФНЧ в других точках – наблюдаются пульсации АЧХ в ПП и боковые лепестки в ПЗ. Данный эффект носит название эффекта Гиббса и возникает из-за ограниченности длины импульсной характеристики. Эффект Гиббса – негативный эффект, который не позволяет получить КИХ фильтр высокой избирательности. Примечательным свойством эффекта Гиббса является тот факт, что уровень приобретаемой неравномерности в полосе пропускания и уровень боковых лепестков в полосе заграждения не уменьшается с ростом количества коэффициентов фильтра. 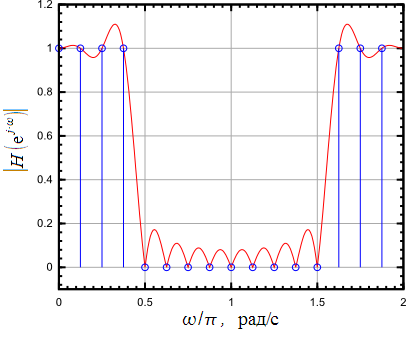 Рис. 19.9 – АЧХ рассчитанного ФНЧ Физический смысл эффекта Гиббса заключается в следующем: при дискретизации АЧХ мы задаём точки, через которые должна пройти АЧХ рассчитанного фильтра, однако мы не накладываем никаких ограничений на поведение АЧХ в других точках. При расчёте мы получаем набор коэффициентов КИХ фильтра как разложение в ряд Фурье комплексного коэффициента передачи. Эти коэффициенты разложения мы рассчитываем через обратное дискретное преобразование Фурье. Поскольку мы ограничиваем количество коэффициентов разложения (количество коэффициентов КИХ фильтра), то получаем усечённый ряд, который лишь аппроксимирует идеальную АЧХ. Аппроксимация будет тем лучше, чем больше коэффициентов импульсной характеристики, т. е. чем чаще мы будем дискретизировать идеальную АЧХ. 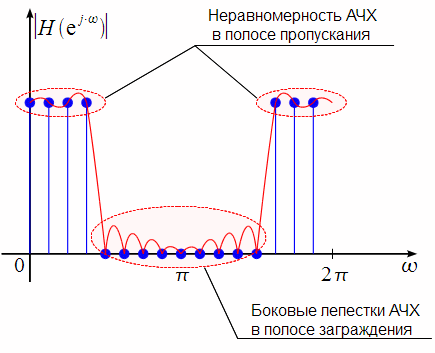 Рис. 19.10 – Эффект Гиббса Синтез КИХ-фильтра методом частотной выборки с оконным сглаживанием (методом окон). Использование весовых окно позволяет улучшить АЧХ КИХ-фильтров. Так как умножение функций во временной области соответствует свёртке этих функций в частотной области, произведение 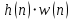 во временной области соответствует свёртке во временной области соответствует свёртке 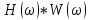 в частотной области. в частотной области.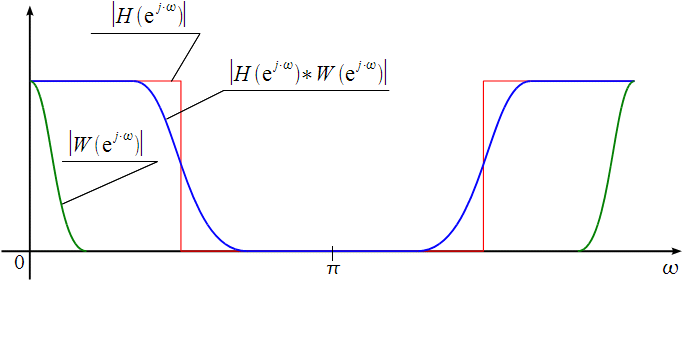 Рис. 19.11 – Свёртка АЧХ идеального ФНЧ и АЧХ оконной функции Таким образом, умножив импульсную характеристику на оконную функцию во временной области, можно получить сглаженную АЧХ фильтра. Окно Кайзера задаётся следующим образом: 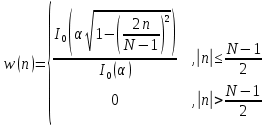 где 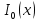 – Функция Бесселя первого рода нулевого порядка – Функция Бесселя первого рода нулевого порядкаПараметр 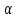 окна Кайзера: окна Кайзера: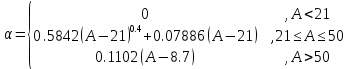 где 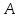 – уровень затухания в ПЗ, дБ – уровень затухания в ПЗ, дБЧастотная характеристика окна Кайзера: 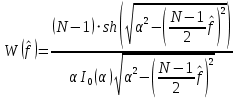 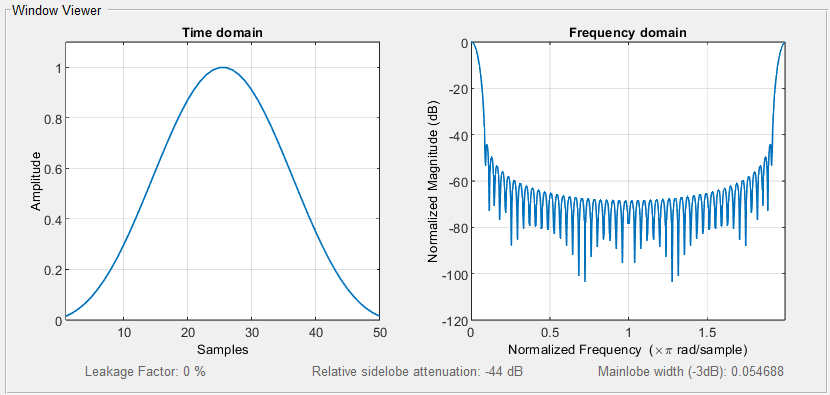 Рис. 19.12 – Пример окна Кайзера с параметром 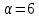
Метод билинейного Z-преобразования, позволяющий синтезировать оптимальный БИХ-фильтр, основан на использовании аналогового фильтра прототипа (АФП). Процедура синтеза БИХ-фильтра на основе АФП включает в себя следующие шаги: Задание требований к характеристике затухания АЧХ (дБ) БИХ-фильтра Формирование требований к АЧХ (дБ) АФП Граничные частоты АФП 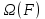 связаны с граничными частотами БИХ-фильтра связаны с граничными частотами БИХ-фильтра 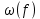 нелинейной зависимостью: нелинейной зависимостью: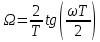 , , 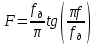 Выбор типа БИХ-фильтра Подобно АФП, четырём видам аппроксимирующих функций соответствуют четыре типа БИХ-фильтров: Баттерворта – с АЧХ, максимально плоской в ПП и монотонной в ПЗ; Чебышева I рода – с АЧХ, равноволновой в ПП и монотонной в ПЗ; Чебышева II рода – с АЧХ, максимально плоской в ПП и равноволновой в ПЗ; Золотарева–Кауэра (эллиптический) – с АЧХ, равноволновой в ПП и ПЗ. Приведённые типы фильтров аппроксимируют амплитудно-частотную характеристику. Расчёт передаточной функции АФП 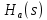 Передаточная характеристика АФП задаётся в дробно-рациональном виде: 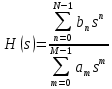 Передаточная функция АФП может быть записана через нули ( 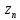 ) и полюсы ( ) и полюсы (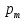 ): ):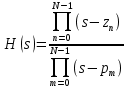 Для физически реализуемого устойчивого фильтра необходимо, чтобы все его полюсы лежали в левой полуплоскости s-плоскости. Для того, чтобы найти физически реализуемый устойчивый фильтр, необходимо рассчитать все нули и полюсы 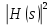 и выбрать только те, что лежат в левой полуплоскости. Они будут определять передаточную характеристику реализуемого фильтра. и выбрать только те, что лежат в левой полуплоскости. Они будут определять передаточную характеристику реализуемого фильтра.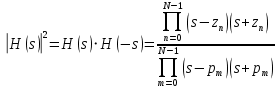 Если имеется передаточная характеристика АФП 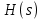 , то проведя замену , то проведя замену 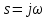 , получим комплексный коэффициент передачи АФП , получим комплексный коэффициент передачи АФП 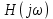 . При этом модуль этого коэффициента будет являться АЧХ фильтра, а аргумент – ФЧХ фильтра. . При этом модуль этого коэффициента будет являться АЧХ фильтра, а аргумент – ФЧХ фильтра.Поскольку нули и полюса обладают квадратной симметрией, то мы всегда будем иметь дело с комплексно-сопряжёнными парами нулей и полюсов и для фильтра второго порядка получим: 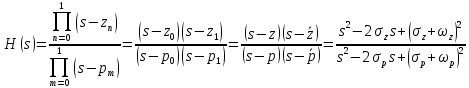 Данное представление называют биквадратной формой (биквадратный фильтр). Фильтр любого чётного порядка может быть представлен при помощи биквадратных форм. Таким образом достаточно рассчитать только половину нулей и полюсов фильтра, а вторая половина будет комплексно-сопряжённой. Преобразование передаточной функции АФП в передаточную функцию БИХ-фильтра 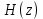 на основе формулы билинейного Z-преобразования на основе формулы билинейного Z-преобразованияБилинейное Z-преобразование основано на замене 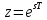 . Данная подстановка позволяет отобразить комплексную s-плоскость АФП в z-плоскость цифрового фильтра. При этом левая полуплоскость s-плоскости (область устойчивости полюсов АФП) отобразится в единичный круг z-плоскости (область устойчивости полюсов ЦФ). . Данная подстановка позволяет отобразить комплексную s-плоскость АФП в z-плоскость цифрового фильтра. При этом левая полуплоскость s-плоскости (область устойчивости полюсов АФП) отобразится в единичный круг z-плоскости (область устойчивости полюсов ЦФ).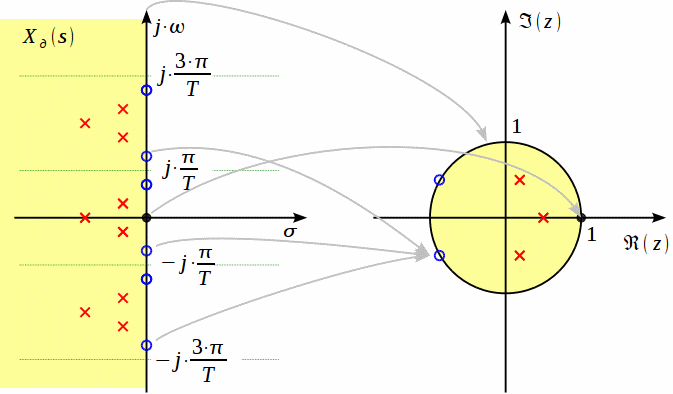 Рис. 20.1 – Графическое отображение s-плоскости в z-плоскость Если имеется передаточная функция АФП 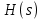 , можно получить передаточную функцию цифрового фильтра: , можно получить передаточную функцию цифрового фильтра: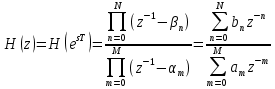 где 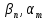 – отображённые на z-плоскость нули и полюса соответственно, – отображённые на z-плоскость нули и полюса соответственно,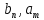 – коэффициенты передаточной функции ЦФ, полученные путём раскрытия произведений нулей и полюсов и приведения подобных слагаемых. – коэффициенты передаточной функции ЦФ, полученные путём раскрытия произведений нулей и полюсов и приведения подобных слагаемых.Однако подстановку 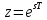 не всегда удобно использовать и вместо неё используют дробно-рациональную подстановку, которая получается из исходной замены при помощи разложения экспоненты в ряд Тейлора с последующим ограничением степени до 1: не всегда удобно использовать и вместо неё используют дробно-рациональную подстановку, которая получается из исходной замены при помощи разложения экспоненты в ряд Тейлора с последующим ограничением степени до 1: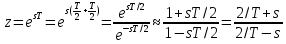 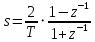 При этом важно понимать, что преобразование через подстановку 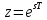 и преобразование через дробно-рациональную подстановку будут давать разные точки z-плоскости из-за усечения ряда Тейлора при разложении экспоненты. Можно заметить, что в первом случае имеет место наложение спектров, а билинейное преобразование исключает этот эффект. и преобразование через дробно-рациональную подстановку будут давать разные точки z-плоскости из-за усечения ряда Тейлора при разложении экспоненты. Можно заметить, что в первом случае имеет место наложение спектров, а билинейное преобразование исключает этот эффект.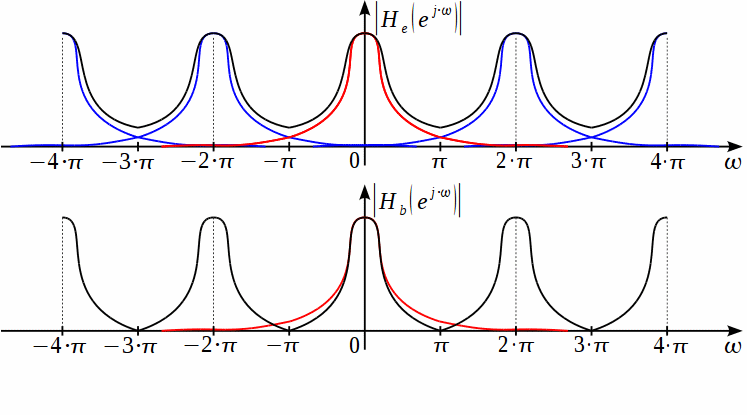 Рис. 20.2 – Разные АЧХ при экспоненциальной (сверху) и билинейной (снизу) подстановках Комплексный коэффициент передачи АФП 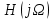 при использовании билинейного преобразования переходит в комплексный коэффициент передачи дискретного фильтра при использовании билинейного преобразования переходит в комплексный коэффициент передачи дискретного фильтра 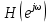 . Процедура обратного билинейного преобразования при . Процедура обратного билинейного преобразования при 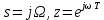 имеет следующий вид: имеет следующий вид: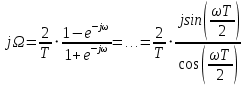 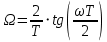 Таким образом, можно заметить, что частоты АФП связаны с частотами ЦФ нелинейным образом (через тангенс). Так как тангенс – периодическая функция, частотная характеристика дискретного фильтра будет периодической функцией с периодом 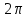 . .Выбор структуры БИХ-фильтра Структура БИХ-фильтра может быть следующей: Каноническая прямая 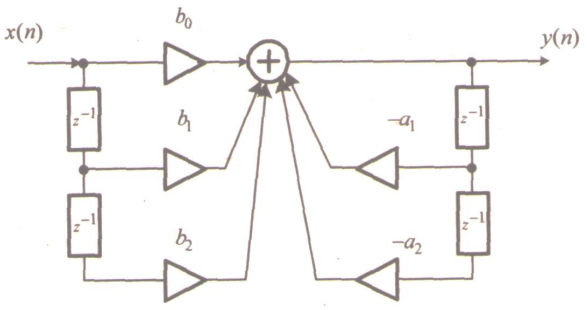 Рис. 20.3 – Пример прямой канонической структуры Каскадная из биквадратных звеньев Каскадной структуре из биквадратных звеньев соответствует представление передаточной функции в виде произведения: 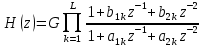 |
