цос. Умноженной на множитель в форме показательной функции W
 Скачать 6.33 Mb. Скачать 6.33 Mb.
|
Разностные уравнения. Решение разностных уравнений с помощью Z-преобразования. Пример решения разностных уравнений с помощью Z-преобразования.Разностные уравнения – это алгоритм функционирования дискретной цепи. Разностное уравнение записывается непосредственно по схеме  Структурная схему по следующему разностному уравнению: Y(nT) = 0,4Х(пТ) - 0,2Y(nT - Т) + 0,3Y(nT - 2Т) 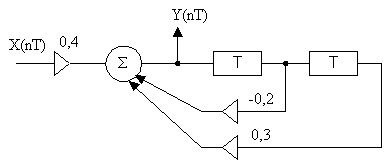 Пример: Составить разностное уравнение по заданной структурной схеме (рис.5) и решить его для заданной последовательности Х(пТ)={1,0; 0,5;0} 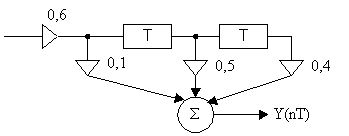 Рисунок 5. Решение: Данной структурной схеме соответствует разностное уравнение Y(nT) = 0,6[0,1Х(nТ) + 0.5Х(nТ - Т) + 0,4Х(nТ - 2Т)] n = 0 → Y(OT) = 0,6*0,1Х(0Т) = 0,06 n = 1 → Y(1T) = 0,6[0,1Х(1Т) + 0,5Х(1Т - Т)]= 0,6*0,1*0,5 + 0,6*0,5*1=0,45 n = 2 → Y(2T) = 0,6[0,1Х(2Т) + 0,5Х(2Т - Т) + 0,4Х(2Т - 2Т)] = = 0,6[0,1*0 + 0,5*0,5 + 0,4*1] = 0,39 Y(nT)= {0,06; 0,45; 0,39} Наряду с разностным уравнением очень часто структуру цифрового фильтра характеризуют передаточной характеристикой. Если разностное уравнение характеризует заданную цепь во временной области, то переда- точная характеристика характеризует эту же цепь в частотной области. Численное выражение для передаточной характеристики равно: 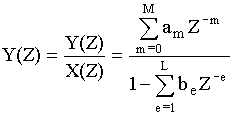 (3) (3)В выражении (3) Y(Z) – Z - преобразование выходного сигнала. X(Z) – Z - преобразование входного сигнала. Z = е -j2π/N: Т - период дискретизации, w - круговая частота, am - коэффициенты передачи нерекурсивной цепи, be - коэффициенты передачи рекурсивной цепи, Z-1 - характеризует задержку сигнала не один тактовый интервал, М, L - соответственно характеризует количество прямых и обратных связей системы. Если 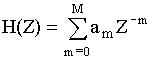 , то цепь называется нерекурсивной. , то цепь называется нерекурсивной.Если 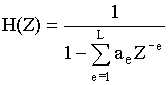 - то цепь рекурсивная. - то цепь рекурсивная. 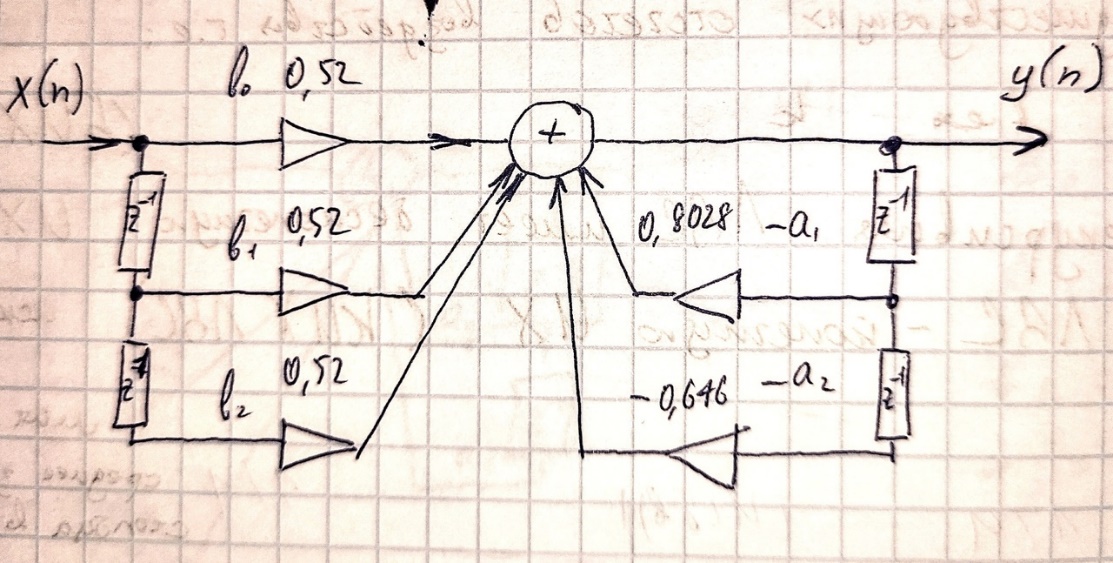 Ну и так-же тут разностное уравнение
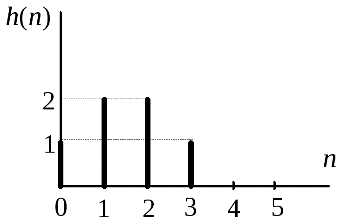
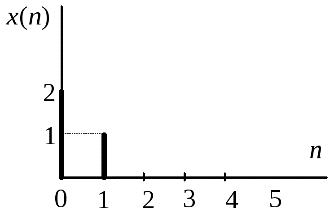
Дискретная система по существу является алгоритмом преобразования одной последовательности (называемой входной) в другую (называемую выходной). Простое представление дискретной системы дано на фиг. 2.3. Входная последовательность обозначена через , а выходная — через . Функционально они связаны соотношением , (2.9) где вид оператора зависит от свойств конкретной системы. Линейная система определяется следующим образом. Если и — некоторые входные последовательности, а и — соответствующие им отклики линейной системы, то при подаче на вход последовательности на выходе образуется последовательность ( и — произвольные постоянные). Система с постоянными параметрами характеризуется тем, что если входной последовательности соответствует выходная последовательность , то входной последовательности при любых соответствует на выходе последовательность . Покажем теперь, что в линейной системе с постоянными параметрами входная и выходная последовательности связаны соотношением типа свертки. Допустим, что — входная, а — выходная последовательности ЛПП-системы, и пусть — отклик системы на единичный импульс, [Последовательность называют импульсной характеристикой системы или откликом на единичный отсчет.] Используя формулу (2.8), можно записать в виде  Фиг. 2.3. Представление дискретной системы.  Фиг. 2.4. Представление линейной системы с постоянными параметрами. Поскольку является откликом системы на последовательность , а параметры системы постоянны, будет откликом на последовательность . Из свойства линейности следует, что откликом на последовательность должна быть последовательность . Поэтому отклик на будет равен Он имеет вид свертки, что и требовалось доказать. Простой заменой переменных равенство (2.11а) может быть преобразовано к виду Таким образом, последовательность полностью описывает ЛПП-систему, что и отражено на фиг. 2.4. На фиг. 2.5 показано, как процесс вычисления свертки осуществляется на практике. На фиг. 2.5, а изображена входная последовательность , отличная от нуля при . На Фиг. 2.5, б приведен пример импульсной характеристики , отличной от нуля при . На фиг. 2.5, в-е представлены и для = 0, 2, 10 и 11. Очевидно, что при и последовательности и не перекрываются равно нулю. На фиг. 2.5, ж приведена последовательность , являющаяся искомой сверткой. 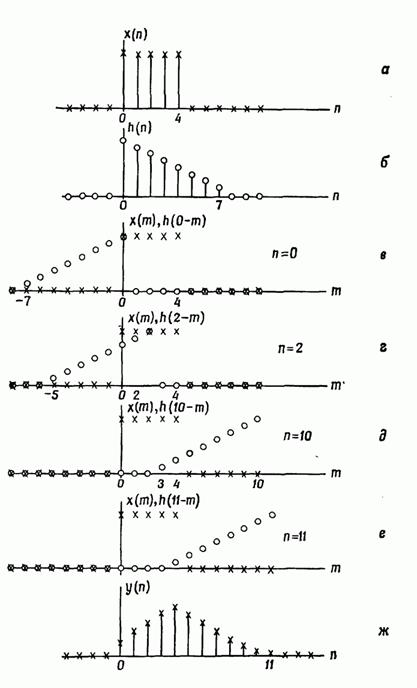 Фиг. 2.5. К образованию дискретной свертки. Импульсной характеристикой линейной дискретной стационарной системы (ЛДСС) называется её реакция на входной сигнал в виде единичного импульса δ[n] при нулевых начальных условиях. Понятие дискретной системы - Под дискретной системой будем понимать техническое устройство или программу, которая осуществляет преобразование дискретной последовательности x n( ) в другую дискретную последовательность y n( ) в соответствии с заданным алгоритмом Представление дискретной системы Алгоритм преобразования входной последовательности x n( ) в выходную последовательность y n( ) По виду оператора R дискретные системы делят: на линейные или нелинейные; стационарные или нестационарные; физически реализуемые (каузальные) или нереализуемые (некаузальные). Описание дискретных систем во временной области Во временной области основной характеристикой ЛДС является импульсная характеристика. Импульснойхарактеристикой(ИХ) Рис. 1.6. К определению импульсной характеристики Соотношение вход/выход ЛДС отображает взаимосвязь между ее входным Во временной области соотношение вход/выход может описываться одним из двух разновидностей линейных уравнений: формулой свертки(название уравнения), если для определения реакции используется импульсная характеристика; разностным уравнением, если для определения реакции используются параметры ЛДС (см. п. 1.3.2). Формула свертки Получим уравнение взаимосвязи между входным - по определению: воздействию в виде цифрового единичного импульса соответствует реакция, называемая импульсной характеристикой - на основании свойства инвариантности во времени для стационарных линейных систем: воздействию, задержанному на время - на основании свойства однородности линейных систем: умножению воздействия на весовой коэффициент – константу - на основании свойства аддитивности линейных систем: реакция на сумму воздействий равна сумме реакций на каждое из воздействий - слева имеем воздействие в виде суммы (1.5) а справа – реакцию где Линейное уравнение (1.10) называют формулой свертки, согласно которой реакция Выполнив замену переменных в (1.10), можно получить другой вариант записи формулы свертки Для нормированного времени формула свертки в двух вариантах записи (1.10) и (1.11) принимает вид соответственно Выбор варианта формулы свертки определяется удобством применения в конкретном случае. Линейная дискретная система, соотношение вход/выход которой описывается в виде формулы свертки, отвечает условиям физической реализуемости: при нулевых начальных условиях (1.9) реакция не может возникнуть раньше воздействия; значения реакции в каждый момент времени зависят только от текущего и предшествующих значений воздействия, но не зависят от его последующих значений. Линейные уравнения (1.12)–(1.13) решаются методом прямой подстановки при нулевых начальных условиях, поэтому формула свертки непосредственно описывает алгоритм вычисления реакции по известному воздействию и импульсной характеристике ЛДС. Пример 1.1.Вычислить реакцию ЛДС по формуле свертки. Импульсная характеристика и воздействие заданы графически (рис. 1.7–1.8). Требуется определить восемь отсчетов реакции.
Решение приведено в табл. 1.1, а график вычисленной реакции – на рис. 1.9.
Рекурсивные и нерекурсивные линейные дискретными системы Линейная дискретная система называется рекурсивной, если хотя бы один из коэффициентовk разностного уравнения (1.15) не равен нулю: Порядкомрекурсивной ЛДС называют порядок РУ (1.15), т. е. Согласно (1.15) реакция y(n)рекурсивнойЛДС в каждый момент времениnопределяется: текущим отсчетом воздействия x(n); предысторией воздействия предысторией реакции Примеры разностных уравнений рекурсивной ЛДС: первогопорядка второгопорядка Линейная дискретная система называется нерекурсивной, если все коэффициенты Для нерекурсивной ЛДС разностные уравнения (1.14)–(1.15) принимают вид соответственно Порядокнерекурсивной ЛДС равен Согласно РУ (1.19) реакция текущим отсчетом воздействия предысторией воздействия Пример РУ нерекурсивной ЛДС второго порядка: |