цос. Умноженной на множитель в форме показательной функции W
 Скачать 6.33 Mb. Скачать 6.33 Mb.
|
Понятие о циклической (круговой) свертке. Связь круговой свертки и ДПФ. Использование циклической свертки для вычисления линейной свертки. Быстрая свертка через БПФ. Примеры.Понятие о циклической свертке: Пусть имеется две последовательности 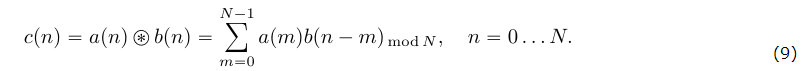 Как можно видеть из (9) циклическую свертку можно выполнять только над последовательностями равной длины отсчетов, причем результатом также будет последовательность длины . Графически пример вычисления циклической свертки (9) для  Рисунок 5. Пример вычисления циклической свертки Заметим, что вычисление циклической свертки можно представить в матричной форме: 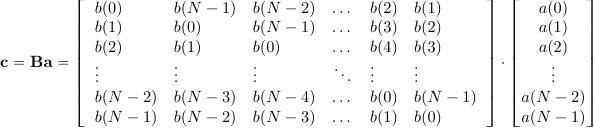 (10) Можно видеть, что каждый столбец матрицы циклически задержан на один отсчет относительно предыдущего столбца. Особая структура матрицы допускает разработку высокоэффективных алгоритмов расчета циклической свертки [2]. Про связь Циклической свертки и ДПФ (немного) и Алгоритм быстрого вычисления циклической свертки на основе БПФ: Важнейшим свойством циклической свертки является то, что она сводится к произведению спектров ДПФ исходных последовательностей, а также к произведению их -образов. Использование аппарата быстрого преобразования Фурье обеспечивает высочайшую вычислительную эффективность циклических сверток. Как мы знаем из свойств дискретного преобразования Фурье, ДПФ циклической свертки равно произведению спектров сворачиваемых сигналов: 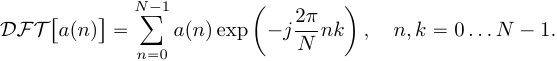 (12) (12)Таким образом перемножив поэлементно спектры ДПФ исходных сигналов, и в взяв обратное дискретное преобразование Фурье, мы получим результат циклической свертки где Схематично процесс расчета циклической свертки сигналов и использованием алгоритмов быстрого преобразования Фурье показан на рисунке 6. 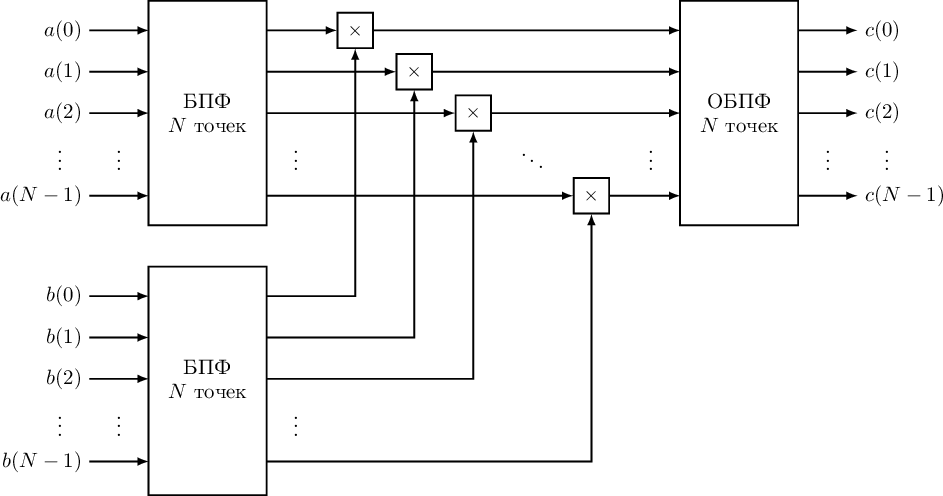 Рисунок 6. Вычисление циклической свертки на основе БПФ Заметим, что эффективность алгоритмов БПФ зависит от длины выборки . Наиболее эффективные алгоритмы разработаны для длины равной целой степени двойки (так называемые алгоритмы по основанию два). При этом помимо высокой вычислительной эффективности, алгоритмы БПФ по основанию два отличаются регулярными структурами при аппаратной и программной реализации, а также прекрасно распараллеливаются при мультипроцессорной обработке. Например для Каждое из трех БПФ требует количество умножений равное: (14) тогда получаем, что расчет свертки через БПФ требует Использование циклической свертки для вычисления линейной свертки. Вычислительные преимущества, которые мы получаем при использовании аппарата БПФ для расчета циклической свертки, хотелось бы также получать и для расчета линейной свертки. С этой целью рассмотрим способ приведения линейной свертки последовательностей ограниченной длительности к циклической. Пусть 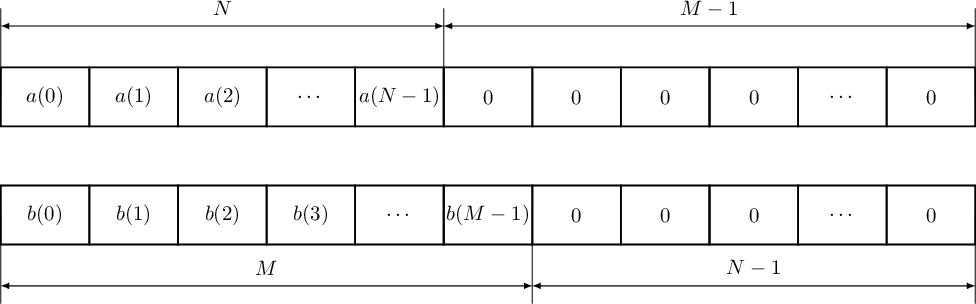 Рисунок 7. Добавление нулей для приведения линейной свертки к циклической К последовательности 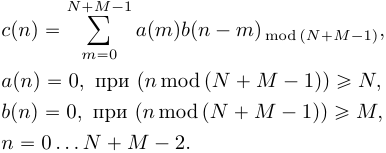 (15) Можно показать, что циклическая свертка (15) дополненных нулями последовательностей, соответствует расчету линейной свертки исходных сигналов. Чтобы убедиться в этом, достаточно использовать матричную запись циклической свертки, и расписать соответствующие элементы Необходимо заметить, что добивать Например при
Проектирование ЦФ выполняется в три этапа: Синтез ЦФ. Включает следующие основные шаги: Выбор типа ЦФ Двум типам ЛДС – КИХ и БИХ – соответствуют два типа ЦФ: КИХ-фильтр (FIR Filter – Finite Impulse Response Filter); БИХ-фильтр (HR Filter – Infinite Impulse Response Filter). Задание требований к характеристикам ЦФ Для ЧИФ (ФНЧ, ФВЧ, ПФ, РФ) в виде требований предъявляют: Частота дискретизации; Граничные частоты полос пропускания\затухания; Минимальный уровень ослабления в ПЗ; Допустимые уровни пульсации АЧХ в ПП и ПЗ; Линейность ФЧХ. Выбор метода синтеза Метод синтеза зависит от типа ЦФ (КИХ или БИХ), а в рамках одного типа – от специфики дополнительных требований (простоты метода, оптимальности проектируемого фильтра и др.). Расчёт передаточной функции ЦФ Выбор структуры ЦФ Моделирование структуры ЦФ с учётом эффектов квантования Реализация структуры ЦФ Структура ЦФ может быть реализована на базе цифрового устройства – цифрового процессора обработки сигналов (ЦПОС), программируемой логической интегральной схеме (ПЛИС) и т. п. Физический смысл свойства линейности ФЧХ – постоянная групповая задержка фильтра. Групповая задержка – время задержки реакции фильтра относительно воздействия. В общем случае (при нелинейной ФЧХ) при разных частотах сигнала воздействия, время задержки разное и зависит от частоты входного воздействия. Пример. Пусть на фильтр оказали гармоническое воздействие 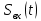 с частотой с частотой 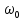 и получили реакцию и получили реакцию 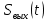 . При этом между входным и выходным сигналами наблюдается разница фаз, равная . При этом между входным и выходным сигналами наблюдается разница фаз, равная 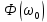 , которой соответствует величина задержки по времени , которой соответствует величина задержки по времени 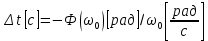 . .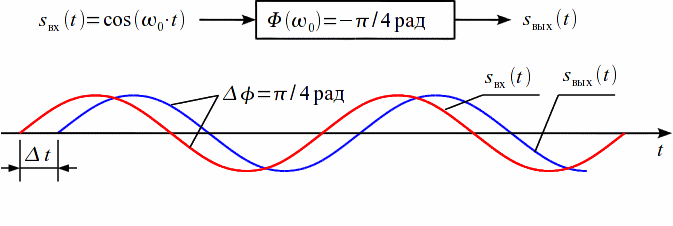 Рис. 19.1 – Пример гармонического воздействия и реакции фильтра (с задержкой) В общем случае время задержки определяется следующим образом: 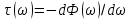 В случае линейной ФЧХ время задержки для всех частот одинаковое, т.к. производная линейной функции есть константа: 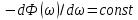 . Так как все гармоники воздействия будут приходить на выход с одинаковой задержкой, форма сигнала не исказится, а время задержки можно будет скомпенсировать. . Так как все гармоники воздействия будут приходить на выход с одинаковой задержкой, форма сигнала не исказится, а время задержки можно будет скомпенсировать.Если же сигнал проходит через фильтр с нелинейной ФЧХ, какие-то гармоники воздействия будут приходить на выход быстрее, чем другие, что приведёт к искажениям формы сигнала. 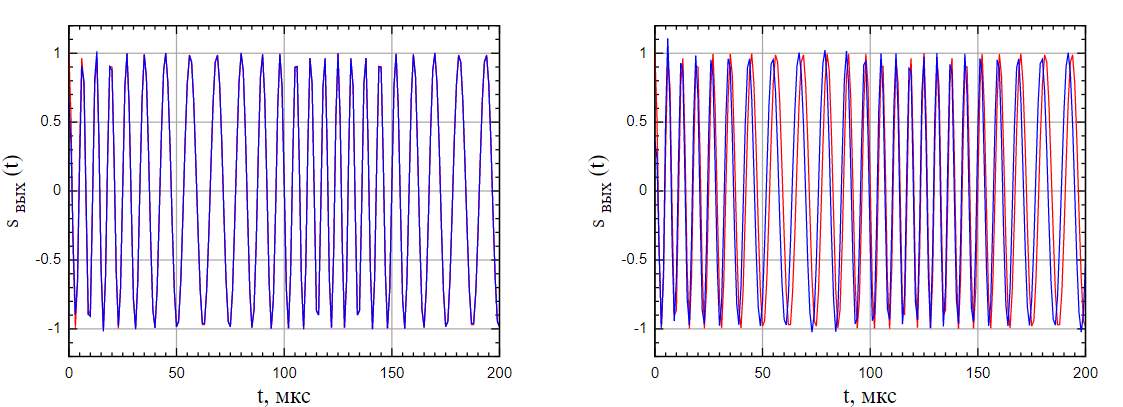 Рис. 19.2 – Демонстрация разницы ГВЗ при линейной (слева) и нелинейной (справа) ФЧХ Условием линейной ФЧХ КИХ-фильтра является симметрия\антисимметрия его ИХ. Доказательство. Пусть линейная ФЧХ будет иметь следующий вид: 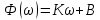 . .Для дальнейшего доказательства напомним, что комплексная передаточная функция и импульсная характеристика фильтра связаны между собой преобразованием Фурье: 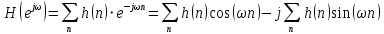 Запишем ФЧХ через комплексную передаточную функцию фильтра и составим уравнение: 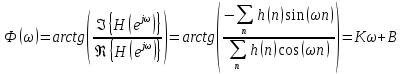 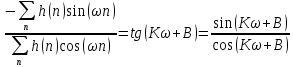 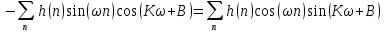 По формуле 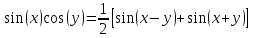 : :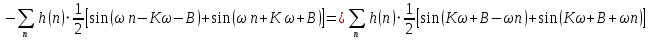 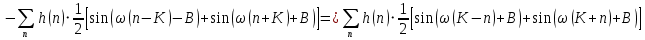 Внесём знак «-» внутрь суммы синусов левой части уравнения и преобразуем: 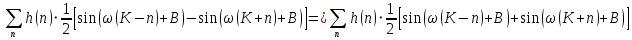 Перенесём правую часть в левую и сократим подобные: 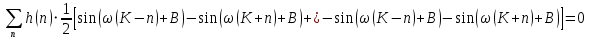 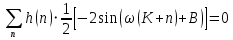 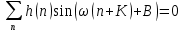 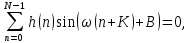 где 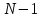 – порядок КИХ-фильтра. – порядок КИХ-фильтра.Получили условие линейной ФЧХ. Рассмотрим 2 частных, самых очевидных случая, когда оно будет выполняться. Эти случаи базируются на понятиях симметричной\антисимметричной ИХ, хотя ЛФЧХ можно достичь и при нарушении симметрии ИХ, однако здесь это не описывается. Уравнение будет выполняться если множители под суммой (отсчёты ИХ и гармонический сигнал) будут обладать свойством чётности\нечётности относительно центра ИХ, причём поочерёдно: ИХ чётна, гармонический сигнал нечётен (синус) Для получения синуса коэффициент 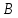 должен быть кратен должен быть кратен 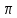 , а коэффициент , а коэффициент 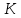 должен центрировать синус к центру ИХ КИХ-фильтра, то есть должен центрировать синус к центру ИХ КИХ-фильтра, то есть 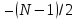 . .При таких коэффициентах уравнение примет вид: 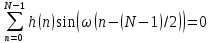 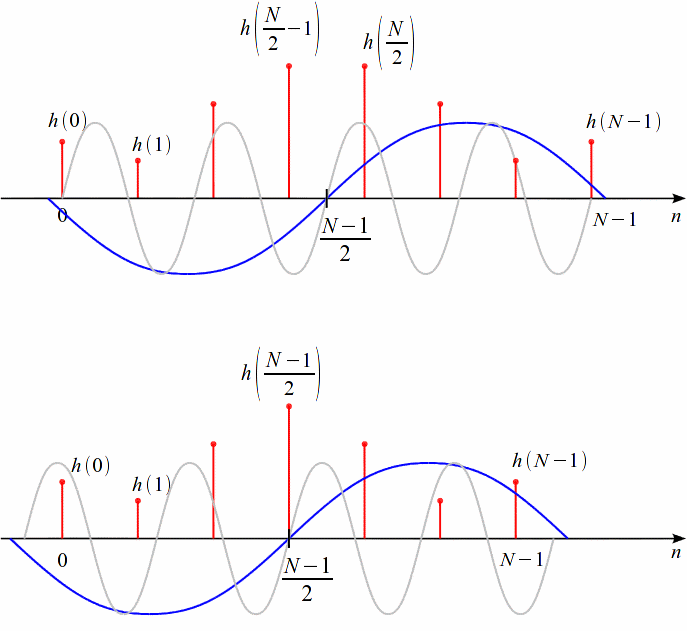 Рис. 19.3 – Примеры симметричной ИХ при чётном и нечётном порядках фильтра ИХ нечётна, гармонический сигнал чётен (косинус) Для обеспечения чётности гармонического сигнала коэффициент 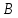 должен быть равен должен быть равен 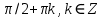 . При таких коэффициентах уравнение примет вид: . При таких коэффициентах уравнение примет вид: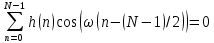 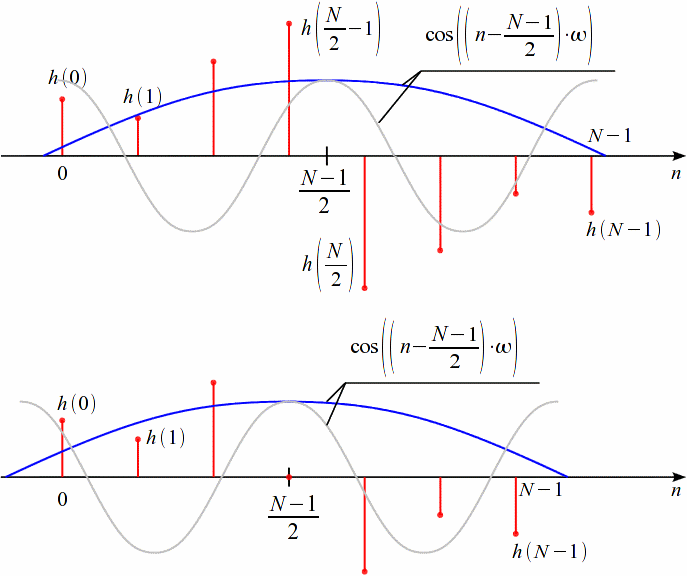 Рис. 19.4 – Примеры антисимметричной ИХ при нечётном и чётном порядках фильтра |
