цос. Умноженной на множитель в форме показательной функции W
 Скачать 6.33 Mb. Скачать 6.33 Mb.
|
|
4. (материал из методички) По карте нулей и полюсов можно определить местоположение максимумов, минимумов и нулей АЧХ в основной полосе частот [0; π], а именно: частота комплексно сопряженного полюса 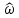 *k, где *k, где 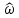 *k = *k = 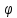 *k в (34), соответствует частоте максимума АЧХ (приблизительно); *k в (34), соответствует частоте максимума АЧХ (приблизительно);частота комплексно сопряженного нуля 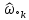 , где , где 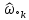 = = 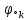 (34), соответствует частоте минимума АЧХ (приблизительно), если (34), соответствует частоте минимума АЧХ (приблизительно), если 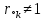 , или нуля АЧХ, если , или нуля АЧХ, если 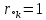 (комплексно сопряженные нули на единичной окружности); в точке нуля АЧХ наблюдается скачок ФЧХ на π; (комплексно сопряженные нули на единичной окружности); в точке нуля АЧХ наблюдается скачок ФЧХ на π;вещественным нулям 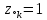 и/или и/или 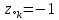 (на единичной окружности) соответствует нуль АЧХ на границе основной полосы частот 0 и/или π. (на единичной окружности) соответствует нуль АЧХ на границе основной полосы частот 0 и/или π.Формула 34 Комплексно сопряженные нули 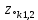 и полюсы и полюсы 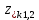 представляют в показательной форме, где аргументы – углы (в радианах) на комплексной z – плоскости: представляют в показательной форме, где аргументы – углы (в радианах) на комплексной z – плоскости: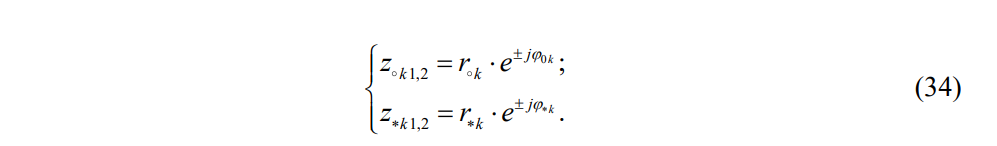
Во временной области: Сигналы (аналоговые и дискретные) описываются функциями времени; Линейные системы (аналоговые и дискретные) описываются: * Характеристиками. Характеристика линейной системы определяется как ее реакция на некоторый тестовый сигнал, т. е. характеристика — это сигнал, описываемый функцией времени; * Соотношением вход/выход. Соотношение вход/выход линейной системы описывается линейным уравнением, устанавливающим связь между входным и выходным сигналами - функциями времени. По умолчанию будем считать, что системы имеют одни вход и один выход. Тип функции времени определяется типом сигнала, а именно: Непрерывная функция х(t) описывает аналоговый сигнал; Последовательность (решетчатая функция) х(nT) описывает дискретный сигнал. Помимо временной, сигналы и линейные системы могут описываться и в других областях (в областях иных независимых переменных), при этом соответствующие функции времени преобразуются в функции другой переменной. Математическое описание аналоговых сигналов и линейных систем в р-области (на комплексной р-плоскости) и в частотной области основано соответственно на преобразованиях Лапласа и Фурье функции времени, для которой выполняется условие 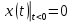 Представление аналоговых сигналов в частотной области: спектр периодических сигналов и спектральная плотность апериодических сигналов. О СПЕКТРЕ Формула ряда Фурье, переписанная в вид: 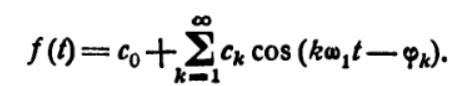 , где , где Сложная периодическая функция определяется совокупностью ck и φk. Совокупность величин ck носит название спектра амплитуд. Совокупность величин φk называется спектром фаз. Спектр периодической функции можно изобразить графически. Выберем для этого координаты ck и ω = kω1. Спектр будет изображён в этой системе совокупностью дискретных точек, т.к. каждому значению kω1 соответствует определённое ck. График, состоящий из отдельных точек неудобен, поэтому принято изображать амплитуды отдельных гармоник вертикальными отрезками соответствующей длины. В результате спектр периодической функции принимает вид: 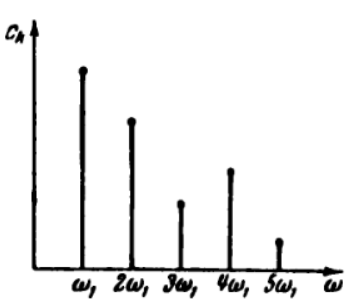 (рис. 1) (рис. 1)Это дискретный спектр, его так же называют линейчатым. Второе свойство спектра (рис. 1) состоит в том, что спектр гармонический. Т.е. состоит из равноотстоящих спектральных линий; частоты гармоник находятся в простых кратных соотношениях. Отдельные гармоники могут отсутствовать (амплитуда равна нулю), но это не нарушает гармоничности спектра. 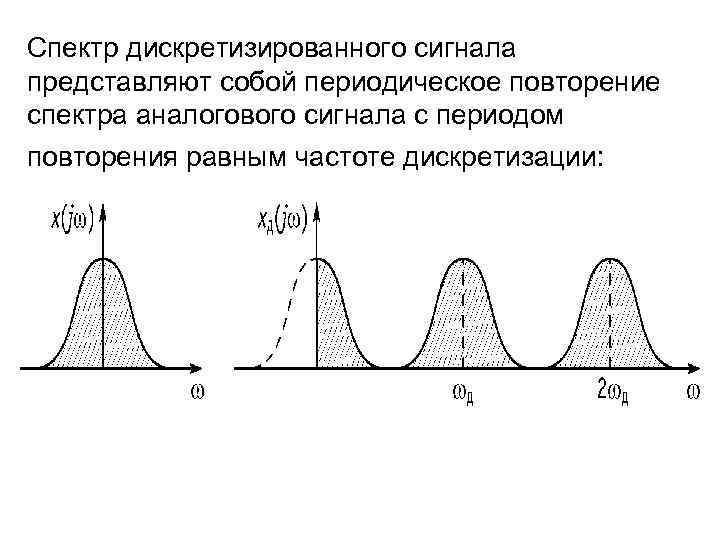 (КАРТИНКА С ИНЕТА) О СПЕКТРАЛЬНОЙ ПЛОТНОСТИ Обращаясь к спектрам непереодических функций. Как известно, в результате предельного перехода от ряда к интегралу Фурье интервалы между отдельными спектральными линиями неограниченно сокращаются, линии сливаются, и вместо дискретных точек спектр должен изображаться непрерывной последовательностью точек, т.е. непрерывной кривой. Такого рода спектр называется сплошным. Следует ввести уточнение. Ранее была записана формула интеграла Фурье в виде: 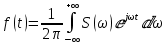 Подинтегральная функция выражает отдельное, бесконечно малое слагаемое, т.е. колебание с бесконечно малой амплитудой dC: 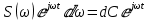 Отсюда находим: 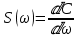 Таким образом величина S(ω) выражает не непосредственно амплитуду, а спектральную плотность. Однако обычно эту деталь опускают и называют S(ω) комплексным спектром непериодической функции, а абсолютное значение (модуль) этой величины просто спектром. 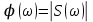 Их связь, физический смысл и размерность. (Инфа не найдена) Свойства интегрального преобразования Фурье (линейность, сдвиг во временной области, сдвиг в частотной области, преобразование произведения сигналов, преобразование свертки сигналов). (Тут всё с инета, т.к. в книгах инфы не найдено) Свойство линейности Пусть даны непериодические сигналы a(t) и b(t), а также их спектральные плотностиA(ω) и B(ω) соответственно. Везде далее мы будем предполагать, что a(t) и b(t) — абсолютно интегрируемые сигналы, тогда преобразование Фурье сигнала s(t) = a(t) + b(t) равно Следствием является свойство умножения на константу : Свойство временного сдвига Рассмотрим сигнал s(t) = a(t – τ) как результат временного сдвига исходного сигнала a(t) на произвольную величину τ. Тогда преобразование Фурье сигнала s(t) имеет вид: 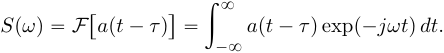 (3) (3)Введем замену переменной ξ = t - τ, тогда t = ξ + τ и dt = dτ. При любом конечном τ пределы интегрирования не меняются и спектральная плотность s(ω) равна: 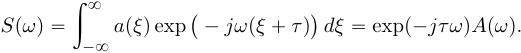 (4) (4)Таким образом, задержка сигнала во времени приводит к изменению фазы его спектральной плотности без изменения амплитуды. Сдвиг в частотной области Сдвиг аргумента спектральной плотности X(f) по частоте на f0 эквивалентен умножению во временной области на множитель 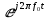 . .Доказательство: 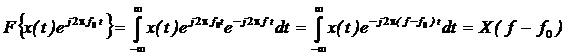 . .Умножение комплексной экспоненты 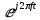 с частотой f0 на функцию x(t) математически означает амплитудную модуляцию (АМ) комплексной экспоненты с частотой f0 на функцию x(t) математически означает амплитудную модуляцию (АМ) комплексной экспоненты 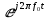 (комплексной несущей) низкочастотным сигналом x(t). (комплексной несущей) низкочастотным сигналом x(t).Разновидности АМ с гармонической несущей . В АМ радиовещании (длинные и средние волны) амплитудно – модулированный сигнал имеет вид В соответствии со свойством модуляции Представив по формуле Эйлера Т.о., при АМ происходит перенос низкочастотного спектра сигнала на частоту модуляции f0. Преобразование Фурье произведения сигналов Пусть сигнал s(t) = a(t)b(t) представляет собой произведение сигналов a(t) и b(t). Преобразование Фурье сигнала s(t) равно: 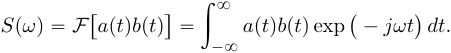 (8) (8)Подставим в (8) вместо сигнала a(t) обратное преобразование Фурье его спектральной плотности A(ω): 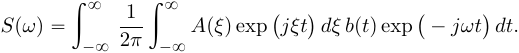 (9) (9)Поменяем в (9) операции интегрирования и получим: 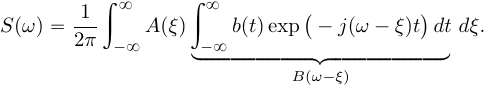 (10) (10)Тогда окончательно преобразование Фурье произведения сигналов пропорционально свертке спектральных плотностей этих сигналов. Преобразование Фурье свертки сигналов Пусть сигнал s(t) представляет собой свертку сигналов a(t) и b(t): 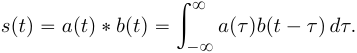 (5) (5)Тогда спектральная плотность сигнала s(t) равна: 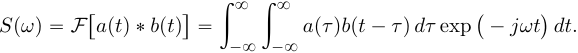 (6) (6)Поменяем порядок интегрирования, и используем свойство (4) временного сдвига: 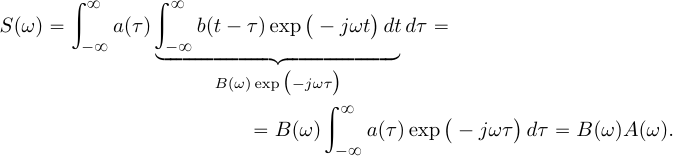 (7) (7)Таким образом, спектральная плотность S(ω) свертки двух сигналов равна произведению их спектральных плотностей. Это одно из важнейших свойств спектрального анализа, которое позволяет анализировать системы обработки в частотной области, заменяя трудоемкое вычисление свертки сигналов произведением их спектральных плотностей.
 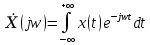 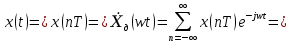 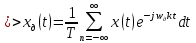 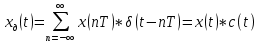 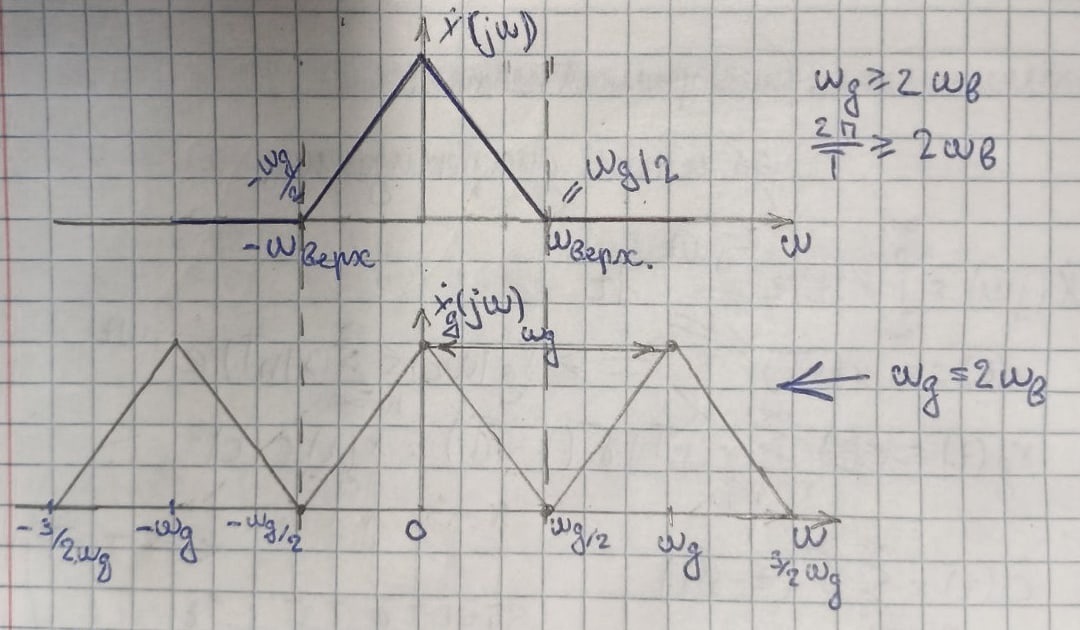  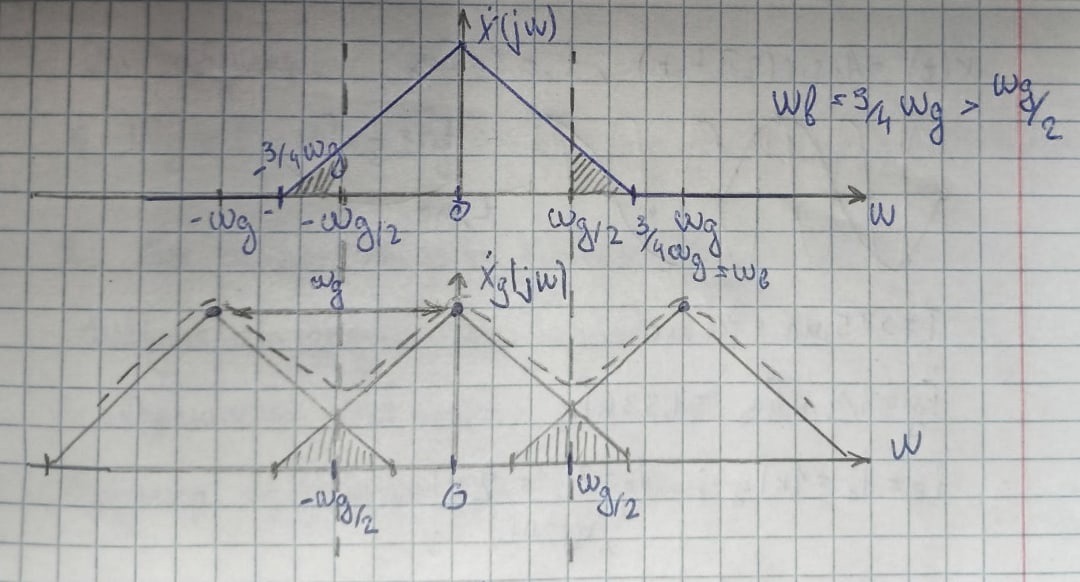 При удовлетворении условий теоремы Котельникова спектральная плотность сигнала после дискретизации является периодической последовательностью спектральных плоскостей непрерывной функции с периодом Wд без взаимных наложений и пересечений (наложение спектров отсутствует) При удовлетворении условий теоремы Котельникова спектральная плотность сигнала после дискретизации является периодической последовательностью спектральных плоскостей непрерывной функции с периодом Wд без взаимных наложений и пересечений (наложение спектров отсутствует)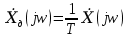 Явление, при котором высококачественные спектральные компоненты исходного непрерывного сигнала отожествляется с низкочастотными компонентами после дискретизации, называется наложением спектров. Все компоненты непрерывного сигнала, лежащие за пределами основного диапазона частот наложаться внутрь основного диапазона частот после дискретизации. Спектральная плотность дискретного сигнала  является периодической функцией частоты с периодом Wд независимо от выполнения теоремы Котельникова. является периодической функцией частоты с периодом Wд независимо от выполнения теоремы Котельникова.
Основная формулировка теоремы: Любой непрерывный сигнал с конечным спектром (имеющим максимальное значение Теорема показывает, что сигнал можно заменить его дискретными значениями, и дает правило на вычисление шага дискретизации Так же важной характеристикой фильтра является его импульсная характеристика, так как она позволяет рассчитать сигнал на выходе фильтра. это есть отклик фильтра на дельта функцию, то есть на импульс бесконечно малый по времени и бесконечно большой по амплитуде. Процесс восстановления сигнала Для восстановления аналогового непрерывного сигнала необходимо, прежде всего, подать последовательность цифровых отсчетов на ЦАП (рис.), а затем полученный на его выходе электрический дискретный и квантованный сигнал пропустить через ФНЧ. Если спектр исходного сигнала был ограничен частотой FВ, то частота среза ФНЧ выбирается равной FВ. Частота дискретизации FД при этом должна была быть взята в соответствии с теоремой Котельникова равной 2FВ. Однако, все рассмотренное выше основывалось на некоторых идеализированных условиях. Рассмотрим некоторые проблемы, возникающие в практических применениях. То как будет выглядеть спектр сигнала после дискретизации на рис. показано при условии что частота дискретизации FД по крайней мере в два раза выше наивысшей частоты спектра. Если уменьшать частоту дискретизации FД, то частичные спектры будут «сходиться» по частотной оси, а при выборе частоты дискретизации FД непозволительно низкой, они будут перекрываться (. При этом восстановить спектр исходного сигнала уже не получится. Исходя из этого определяется минимально допустимая частота дискретизации FД. В соответствии с рассмотренным перефразируем теорему Котельникова следующим образом. Для того чтобы иметь возможность восстановить исходный сигнал после его дискретизации без искажений необходимо, чтобы частота дискретизации FД была бы по крайней мере в два раза выше частоты FВ наивысшей спектральной составляющей, присутствующей в исходном сигнале. Обратим внимание, что в соответствии с нашими прежними рассуждениями, разговор идет не только о возможности восстановления сигнала. Невозможность восстановления сигнала после дискретизации означает потерю информации, которую он нес. Т. е. рассмотренные выше условия определяют минимально допустимую частоту взятия отсчетов исходного непрерывного сигнала при вводе их в цифровую вычислительную систему. 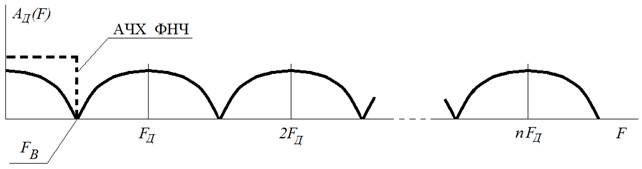 Рис. Определение предельной частоты дискретизации для восстановления спектра исходного сигнала (Вместо Найквиста в нашем унике лучше говорите Котельников Прим. автора) Как видно из рис. предельная частота дискретизации FД, при которой перекрытия частичных спектров еще не происходит, равна удвоенной верхней частоте спектра сигнала, т. е. равна 2FB. Эта частота называется частотой Найквиста. Дискретизация с частотой Найквиста называется предельной дискретизацией. Очевидно, что при выборе частоты дискретизации равной частоте Найквиста АЧХ такого фильтра должна быть идеальной (как это и показано на рис.). Сигнал, дискретизированный с FД > 2FB, называется передискретизированным сигналом. Несмотря на то, что в этом случае получается избыточное число отсчетов, на практике частоту дискретизации FД выбирают именно так. Дискретизация с такой частотой разносит частичные спектры относительно друг друга по частотной оси на большее расстояние. При этом между наивысшей частотой спектра исходного сигала FВ и половиной частоты дискретизации FД/2 будет некоторый интервал, в который можно «поместить» срез АЧХ ФНЧ. Чем больше этот интервал, тем меньше требований к фильтру. Требования к АЧХ аналогового фильтра на входе дискретизатора будут зависеть от того, как близко частотные составляющие частичных спектров (внеполосного сигнала) отстоят от FД/2, а также требуемой величиной их подавления. Построение аналоговых фильтров высокого порядка связано с известными трудностями – требуется применение прецизионных пассивных элементов и высококачественных операционных усилителей с хорошей температурной и временной стабильностью. Кроме того, надо иметь в виду, что всякий фильтр высокого порядка обладает существенно нелинейной фазовой характеристикой. Передискретизация позволяет значительно снизить требования к характеристике аналогового ФНЧ. Даже удвоение Fд дает возможность сделать срез его АЧХ довольно пологим (рис. а). А при увеличении частоты дискретизации в четыре (рис. .б) и более раз, требования к аналоговому ФНЧ снижаются до вполне заурядных. 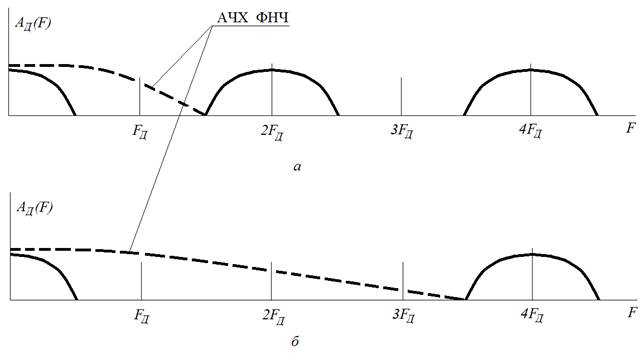 Рис. Требуемые АЧХ аналоговых фильтров после двукратного (а) и четырехкратного (б) повышения частоты дискретизации Чтобы облегчить требования к фильтрации преобразованного сигнала, перед ЦАП можно разместить цифровой фильтр. Выполнить такой фильтр с нужными характеристиками значительно проще, чем аналоговый. Он может иметь достаточно высокий порядок и при этом обладать линейной фазовой характеристикой. Характеристика цифрового фильтра, как и спектр цифрового сигнала, тоже имеет периодическую структуру и тоже повторяется на частотах, кратных частоте дискретизации. Поэтому, если цифровой фильтр будет работать на частоте дискретизации FД, то подавить высокочастотные компоненты все равно не удастся. Проблема может быть решена путем искусственного увеличения частоты дискретизации FД в несколько раз. При этом недостающие значения сигнала вычисляются по известным значениям методами интерполяции (рис. ). Фактически речь идет о «сглаживании» цифрового сигнала перед его подачей на ЦАП, Так как число уровней дискретных отсчетов на выходе цифровой системы при этом увеличивается, то и разрядность ЦАП должна быт увеличена. 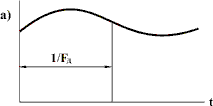 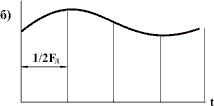 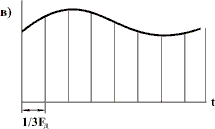 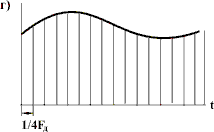
Соотношение (8) носит название дискретного преобразования Фурье (ДПФ), а (3) – обратного преобразования Фурье (ОДПФ) xp(n)= Из определений (3) и (8) видно, что обе последовательности xp(n) и Xp(k) полностью определяются одним периодом xp(n) коэффициенты ДПФ последовательности конечной длины равны значениям z-преобразования этой же последовательности в N точках, равномерно распределенных по единичной окружности. Еще более важный вывод состоит в том, что коэффициенты ДПФ последовательности конечной длины однозначно представляют саму последовательность, т.к. по ним можно точно восстановить исходную последовательность, используя ОДПФ. Итак, хотя ДПФ и ОДПФ вводятся для периодических последовательностей, важно, что через них можно представлять последовательности конечной длины. Свойства: Линейность Если xp(n) и yp(n) – периодические последовательности (с периодом в N отсчетов каждая), а Xp(k) и Yp(k) – их ДПФ, то дискретное преобразование Фурье последовательности xp(n)+ yp(n) равно Xp(k) + Yp(k). Это положение справедливо и для последовательностей конечной длины. |
