цос. Умноженной на множитель в форме показательной функции W
 Скачать 6.33 Mb. Скачать 6.33 Mb.
|
|
1.3.4. Ких- и бих-системы Рассмотрим особенности импульсныххарактеристикрекурсивных и нерекурсивных ЛДС. С этой целью приведем примеры вычисления ИХ по заданному разностному уравнению, решая его методом прямой подстановки при нулевых начальных условиях. Пример 1.3.Вычислить импульсную характеристикунерекурсивнойЛДС второго порядка, соотношение вход/выход которой описывается разностным уравнением (1.20): Решение.Согласно определению ИХ – этореакцияна цифровой единичный импульс (рис. 1.6), поэтому, выполнив замену 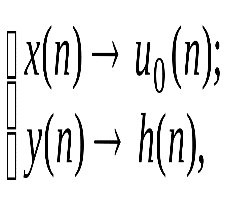 (1.21) (1.21)перепишем РУ в виде и вычислим отсчеты ИХ методом прямой подстановки при нулевых начальных условиях (см. п. 1.3.2): Распространяя полученные результаты на ИХ нерекурсивной ЛДС произвольного порядка, можно сделать следующие выводы: - импульсная характеристика нерекурсивной ЛДС имеет конечную длительность; - значения отсчетов ИХ равны коэффициентам разностного уравнения Поэтому нерекурсивные ЛДС называют системами с конечной импульсной характеристикой (КИХ-системами). Пример 1.4.Вычислить импульсную характеристикурекурсивнойЛДС первого порядка, соотношение вход/выход которой описывается разностным уравнением Решение.Выполнив замену (1.21), перепишем РУ в виде и вычислим отсчеты ИХ методом прямой подстановки при нулевых начальных условиях: Вычисления можно продолжать бесконечно по формуле Распространяя полученные результаты на ИХ рекурсивнойЛДС произвольного порядка, можно сделать вывод: импульсная характеристикарекурсивнойЛДС имеетбесконечнуюдлительность. Поэтому рекурсивные ЛДС называют системами с бесконечной импульсной характеристикой (БИХ-системами). Устойчивость линейных дискретных систем ЛДС называется устойчивой, если при ограниченном воздействии где где Оценка устойчивости по импульсной характеристике Существуют два критерияустойчивости ЛДС. Один из них позволяет оценить устойчивость ЛДС по ее импульсной характеристике во временной области, другой – поz-изображению этой характеристики вz-области (см. п. 1.4). Выбор критерия зависит от удобства его практического использования. Критерий, позволяющей оценить устойчивость ЛДС по ее импульсной характеристике, формулируется следующим образом: для того чтобы ЛДС была устойчива, необходимо и достаточно выполнения условия абсолютной сходимости ряда Данный критерий устойчивости свидетельствует о том, что нерекурсивныеЛДС (КИХ-системы)всегдаустойчивы, поскольку их импульсная характеристика конечна. Прежде чем делать вывод об устойчивости рекурсивных ЛДС, рассмотрим простой пример. Пример 1.5. Определить, устойчива ли рекурсивная ЛДС, импульсная характеристика которой описывается дискретной экспонентой (1.6) Решение. Подставив данную ИХ в правую часть критерия (1.21а), получим ряд представляющий собой сумму бесконечной геометрической прогрессии Как известно, сумма такого ряда в области сходимости, т. е. при В этом случае импульсная характеристика представляет собой затухающуюэкспоненту (см. рис. 1.3), а ЛДС согласно критерию (1.21а) является устойчивой. Вне указанной области, т. е. при а ЛДС по критерию (1.21а) – неустойчивой. В общем случае относительно устойчивости БИХ-систем можно сделать следующие выводы: - рекурсивные ЛДС (БИХ-системы) требуют проверки на устойчивость, - импульсная характеристика устойчивой ЛДС имеет характер затухающей функции времени. 9. Линейные дискретные системы (ЛДС) с постоянными параметрами. Понятие о передаточной функции ЛДС. Связь передаточной функции ЛДС с ее структурой, примеры. Нули и полюса передаточной функции линейной дискретной системы, определение. Условие устойчивости ЛДС, выраженное через требование к полюсам ее передаточной функции. Передаточные функции рекурсивных и нерекурсивных ЛДС, отличия. * Систему называют линейной, если она удовлетворяет принципам суперпозиции (реакция на сумму воздействий равна сумме реакций на данные воздействия) и однородности (воздействию, умноженному на весовой коэффициент, соответствует реакция, умноженная на тот коэффициент). * Систему называют дискретной, если она преобразует дискретное воздействие x(n) в дискретную реакцию y(n), где n – порядковый номер отсчёта (индекс элемента входной или выходной числовой последовательности), отмеряющий момент времени в интервалах дискретизации T. Передаточная функция ЛДС - отношение z-изображения реакции к z-изображению воздействия при нулевых начальных условиях (ННУ): 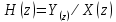 Соотношение можно получить, выполнив z-преобразование разностного уравнения (РУ): 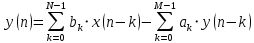 ak, bk - вещественные коэффициенты k – значения задержек воздействия и реакции (N - 1), (M - 1) – константы, определяющие максимальные задержки Связь передаточной функции ЛДС с ее структурой, примеры. Структура ЛДС отображает алгоритм вычисления реакции по РУ и определяется видом передаточной функции. Для рекурсивных звеньев 2-ого порядка с передаточной функцией: 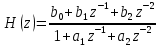 и разностным уравнением 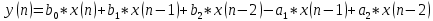 поддерживаются следующие структуры * Прямая форма первого типа – Direct-Form Ⅰ (Рисунок 1) * Прямая транспонированная - Direct-Form Ⅰ Transposed (Рисунок 2) * Прямая каноническая - Direct-Form Ⅱ (Рисунок 3) *Прямая каноническая транспонированная - Direct-Form Ⅱ Transposed (Рисунок 4) 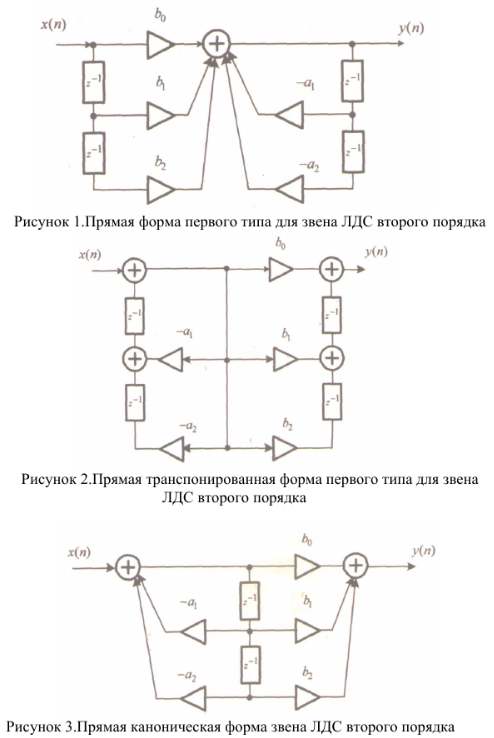 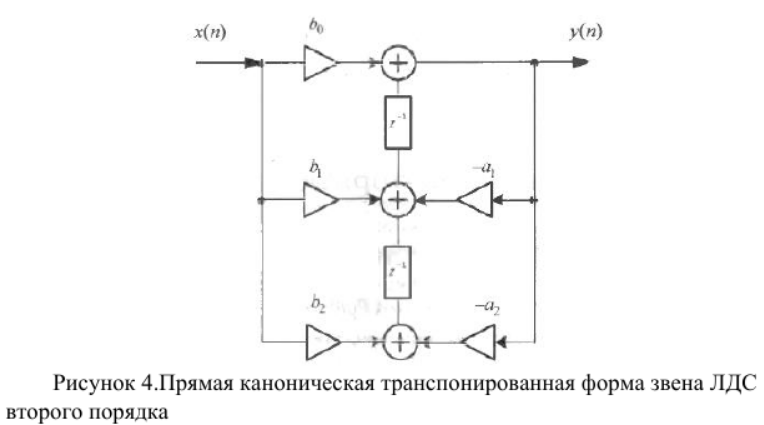 Нули и полюса передаточной функции линейной дискретной системы, определение. Нули – значения z на комплексной плоскости при которых функция равна нулю. Полюса (особые точки) – значения z при которых знаменатель функции равен нулю. Карта нулей и полюсов – z плоскость с нанесённой единичной окружностью и символически изображёнными нулями и полюсами. Условие устойчивости ЛДС, выраженное через требование к полюсам ее передаточной функции. По карте нулей и полюсов можно сделать вывод об устойчивости ЛДС: полюсы располагаются внутри единичного круга с центром в начале координат. Передаточные функции рекурсивных и нерекурсивных ЛДС, отличия.      
ЛДС с постоянными параметрами (из его электронной доски) Делятся на: - устойчивые 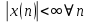 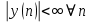 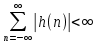 -не устойчивые 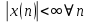 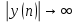 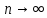 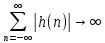 Предварительно можно оценить по графику Если 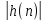 убывающая, то убывающая, то 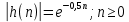 Если 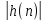 возрастающая, то возрастающая, то 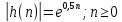 Также ЛДС с постоянными параметрами делятся на: -Физически реализуемая Не нарушает принцип причинности т.е. реакция на выходе цепи не опережает воздействие. 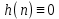 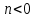 -Физически нереализуемая Контр. пример 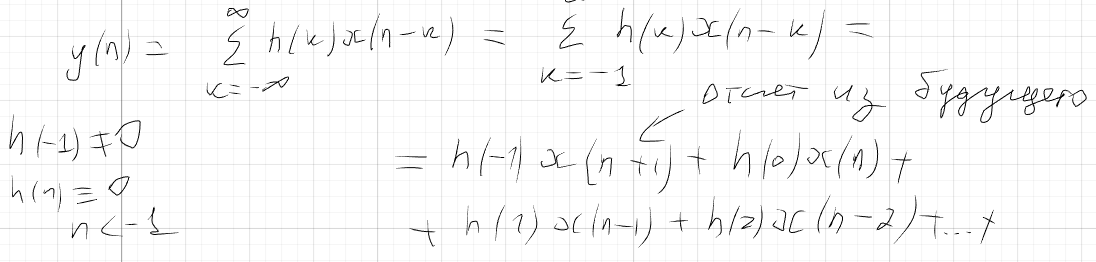 y(n) – отчет реакции в данный момент времени 2. (материал из методички) Основной характеристикой ЛДС в частотной области является частотная характеристика (ЧХ) 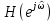 – Фурье-изображение ИХ h(n) : – Фурье-изображение ИХ h(n) : 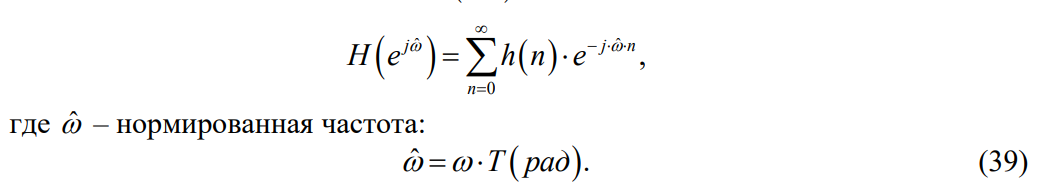 Частотная характеристика 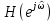 связана с передаточной функцией H z соотношением: связана с передаточной функцией H z соотношением:что позволяет путем подстановки 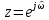 в (32) получить ее в виде: в (32) получить ее в виде: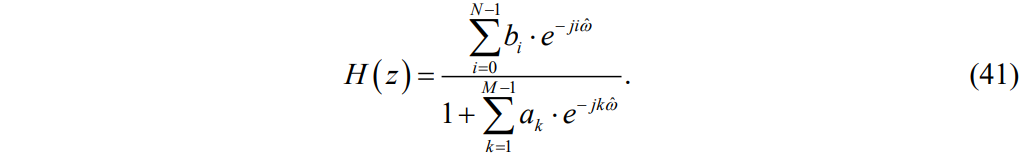 Про формулу 32. Передаточной функцией ЛДС называют отношение z-изображения реакции к z-изображению воздействия при ННУ: Данное отношение легко получить, выполнив Z-преобразование РУ (30). Передаточная функция рекурсивной ЛДС имеет вид дробно-рациональной функции: 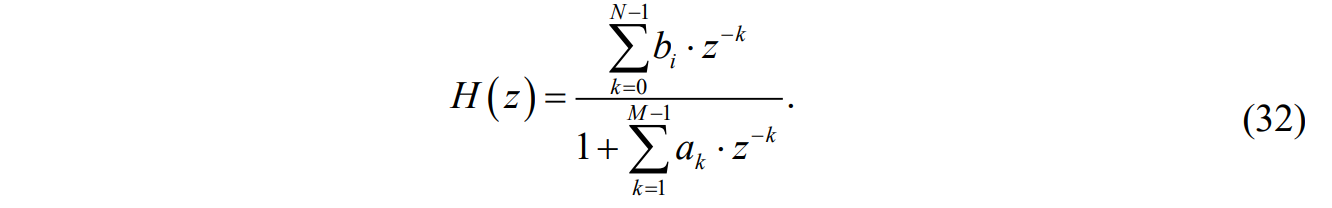 Показатель степени z-k соответствует задержкам воздействия b задержкам реакции; коэффициенты ak передаточной функции и РУ (30) имеют противоположные знаки.Соотношение вход/выход ЛДС, однозначно связанное с его основной характеристикой в z-области – передаточной функцией, имеет вид линейного математического преобразования в виде разностного уравнения (РУ): Про формулу 30 из его электронной доски. Разностное уравнение 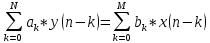 x(n) – воздействие y(n) – реакция k – значения задержек воздействия и реакции ak, bk – вещественные коэффициенты (параметры) РУ N, M – константы, определяющие максимальные задержки R = max(N, M) – порядок ЛДС (порядок фильтра) РУ задаёт алгоритм для нахождения y(n) 3. (материал из методички) Амплитудно-частотная характеристика (АЧХ) отображает частотную зависимость отношения амплитуды реакции к амплитуде гармонического воздействия в установившемся режиме. Фазочастотная характеристика (ФЧХ) отображает частотную зависимость разности фаз реакции и гармонического воздействия в установившемся режиме. АЧХ и ФЧХ – периодические функции с периодом 2π в шкале частот 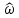 или fд в шкале частот f (Гц). или fд в шкале частот f (Гц).АЧХ – четная, а ФЧХ – нечетная функция частоты. АЧХ и ФЧХ рассчитываются в основной полосе частот [0; π] в шкале частот 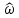 или [0; fд/2 ] в шкале частот f (Гц). или [0; fд/2 ] в шкале частот f (Гц). |
