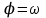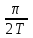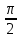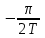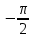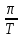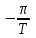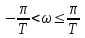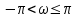цос. Умноженной на множитель в форме показательной функции W
 Скачать 6.33 Mb.
|
|
Аналоговые, дискретные и цифровые сигналы, определение. Процесс дискретизации, пример. Понятие интервала дискретизации, понятие частоты дискретизации, угловой частоты дискретизации и их связь. Процесс квантования и преобразования отсчетов в двоичный код, пример. Связь количества уровней квантования и разрядности кодовых слов на выходе аналогово-цифрового преобразователя, пример. Понятие о нормированной частоте и основном диапазоне частот. Прямое Z – преобразование, определение. Область сходимости, определение, примеры. Свойства (линейность, z-преобразование задержанной копии последовательности, z-преобразование последовательности x(n), умноженной на множитель в форме показательной функции Wn, z-преобразование свертки двух последовательностей). Математическая модель АЦП как идеального амплитудно-импульсного модулятора. Математическая модель дискредитированного во времени сигнала. Преобразование Лапласа и Фурье дискретизированного во времени сигнала. Интервал/период дискретизации, частота и угловая частота дискретизации. Связь прямого Z-преобразования с дискретным преобразованием Лапласа. Отображение P-плоскости в Z-плоскость. Преобразование начала координат, оси частот, левой и правой полуплоскостей из P-плоскости в Z-плоскость. Неоднозначность преобразования P-плоскости в Z-плоскость (наложение множества точек на прямой из P-плоскости в одну точку Z-плоскости). Обратное Z-преобразование. Вычисление обратного z-преобразования с помощью вычетов. Формулы для вычисления вычетов в простых и кратных полюсах. Пример вычисления обратного z-преобразования. Разностные уравнения. Решение разностных уравнений с помощью Z-преобразования. Пример решения разностных уравнений с помощью Z-преобразования. Линейные дискретные системы (ЛДС) с постоянными параметрами. Основные свойства (линейность, инвариантность к сдвигу во времени, физическая реализуемость), формулировка, примеры. Понятие об импульсной характеристике ЛДС. Вычисление реакции ЛДС через импульсную характеристику. Определение устойчивости ЛДС. Требования к импульсной характеристике для устойчивых ЛДС. Линейные дискретные системы (ЛДС) с постоянными параметрами. Понятие о разностном уравнении. Порядок разностного уравнения. Связь разностного уравнения и структуры ЛДС, пример. Рекурсивные и нерекурсивные ЛДС, структурные схемы. Понятие КИХ и БИХ систем. Связь КИХ и БИХ систем с рекурсивными и нерекурсивными системами. Устойчивость КИХ и БИХ систем. Линейные дискретные системы (ЛДС) с постоянными параметрами. Понятие о передаточной функции ЛДС. Связь передаточной функции ЛДС с ее структурой, примеры. Нули и полюса передаточной функции линейной дискретной системы, определение. Условие устойчивости ЛДС, выраженное через требование к полюсам ее передаточной функции. Передаточные функции рекурсивных и нерекурсивных ЛДС, отличия. Линейные дискретные системы (ЛДС) с постоянными параметрами. Частотная характеристика линейной дискретной системы и ее связь с передаточной функцией ЛДС. Амплитудно- и фазочастотная характеристики ЛДС. Связь нулей и полюсов передаточной функции с положениями локальных минимумов и максимумов амплитудно-частотной характеристики на частотной оси. Представление аналоговых сигналов в частотной области: спектр периодических сигналов и спектральная плотность апериодических сигналов. Их связь, физический смысл и размерность. Свойства интегрального преобразования Фурье (линейность, сдвиг во временной области, сдвиг в частотной области, преобразование произведения сигналов, преобразование свертки сигналов). Спектральная плотность непрерывного сигнала до и после дискретизации, и их связь. Спектральная плотность сигнала после дискретизации при условии удовлетворения или не удовлетворения условий теоремы Котельникова. Явление наложения спектров при дискретизации непрерывных сигналов. Примеры. Теорема отсчетов Котельникова во временной области, формулировка. Импульсная характеристика восстанавливающего фильтра, ее свойства. Процесс восстановления наглядно графически, примеры. Интерпретация процесса восстановления непрерывного сигнала в частотной области как идеальная низкочастотная фильтрация дискретизированного во времени сигнала. Дискретное преобразование Фурье (ДПФ) периодических последовательностей. Связь коэффициентов ДПФ периодической последовательности со спектральной плотностью конечной последовательности. Свойства ДПФ (линейность, периодичность, симметрия, сдвиг во временной области, сдвиг в частотной области, преобразование произведения последовательностей, преобразование циклической свертки последовательностей), примеры. Быстрое преобразование Фурье (БПФ) с прореживанием по времени для размера блока N = 2r. Понятие о поворачивающем множителе. Понятие о графе «бабочка» для БПФ с прореживанием по времени, алгоритм его работы. Пример структуры модуля БПФ на основе 8-точечного БПФ. Понятие о бит-реверсной перестановке элементов последовательности. Быстрое преобразование Фурье (БПФ) с прореживанием по частоте для размера блока N = 2r. Понятие о поворачивающем множителе. Понятие о графе «бабочка» для БПФ с прореживанием по частоте, алгоритм его работы. Пример структуры модуля БПФ на основе 8-точечного БПФ. Понятие о бит-реверсной перестановке элементов последовательности. Интеграл свертки. Связь интеграла свертки с образами по Лапласу и Фурье сворачиваемых сигналов. Линейная дискретная свертка. Связь дискретной свертки с Фурье- и Z-образами последовательностей. Использование для вычисления реакции линейной цепи с постоянными параметрами. Примеры. Понятие о циклической (круговой) свертке. Связь круговой свертки и ДПФ. Использование циклической свертки для вычисления линейной свертки. Быстрая свертка через БПФ. Примеры. Этапы проектирования цифровых фильтров. Требования к АЧХ, предъявляемые при синтезе фильтров. КИХ-фильтры с линейной ФЧХ, свойства. Порядок фильтра и длина импульсной характеристики. Проектирование КИХ-фильтров методом окон. Эффект Гиббса и назначение окон (на примере окна Кайзера). Структуры КИХ-фильтров с симметричной и антисимметричной импульсной характеристикой. Этапы проектирования цифровых фильтров. Требования к АЧХ, предъявляемые при синтезе фильтров. Проектирование БИХ-фильтров методом билинейного z-преобразования. Связь порядка фильтра с числом биквадратных звеньев. Нелинейное искажение оси частот при билинейном Z-преобразовании.
Аналоговые, дискретные и цифровые сигналы, определение Аналоговым называют сигнал, непрерывный по времени и состоянию. Такой сигнал описывается непрерывной или кусочно-непрерывной функцией x(t), при этом и аргумент, и функция могут принимать любые значения из некоторых интервалов t1 <= t <= t2 ; x1 <= x <= x2 соответственно. Дискретным называют сигнал, дискретный по времени и непрерывный по состоянию. Такой сигнал описывается решетчатой функцией(последовательностью) x(nT), n=0,1,2..., которая определена только в дискретные моменты nT и может принимать значения из некоторого интервала x1 <= x <=x 2. Интервал T называют периодом дискретизации, а обратную величину - частотой дискретизации 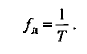 Значения последовательность в моменты времени nT называют отсчетами. Дискретный сигнал может быть как вещественным, так и комплексным. В последнем случае его вещественная и мнимая части описываются вещественными последовательностями:  Цифровым называют сигнал, дискретный по времени и квантованный по состоянию. Такой сигнал описывается квантованной решетчатой функцией (квантованной последовательностью) Xu(nT), отсчеты которой в каждый момент времени nT принимают дискретные значения уровней квантования из некоторого интервала x1 <= x <= x2. 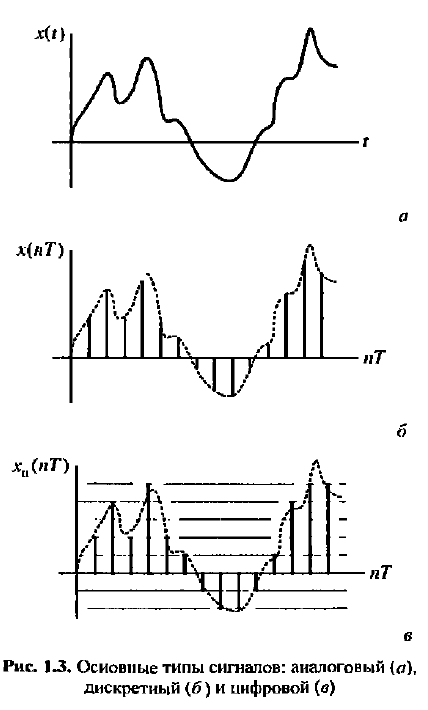 2) Процесс дискретизации, пример 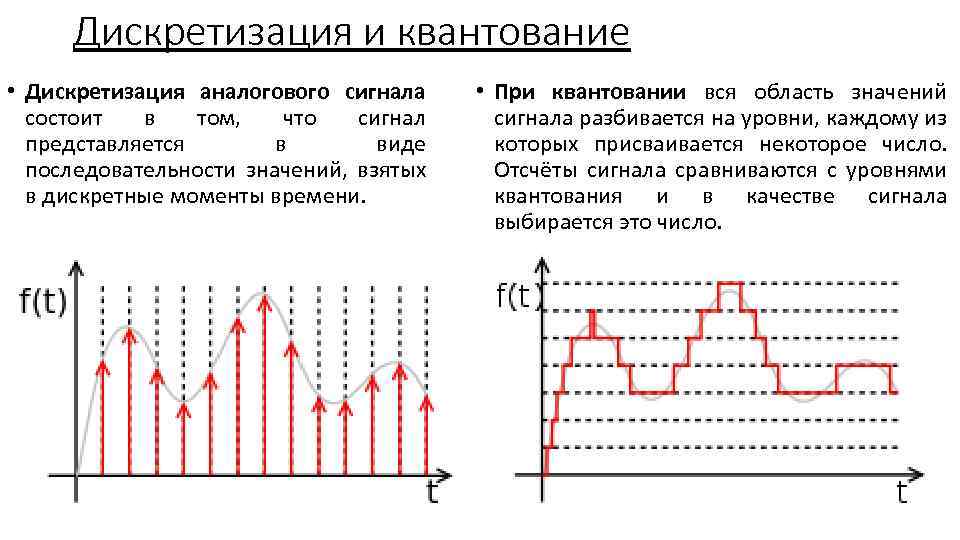 Дискретизация заключается в преобразовании аналогового сигнала в цифровую форму и состоит из двух не связанных друг с другом операций: собственно дискретизации и квантования. Собственно дискретизация -- это процесс определения моментов времени, в которые должны быть произведены отсчеты; квантование -- перевод этих отсчетов в цифровую форму. 3) Понятие интервала дискретизации, понятие частоты дискретизации, угловой частоты дискретизации и их связь. Интервал дискретизации - промежуток времени между соседними отсчетами в масштабе времени. В аналогово-цифровых преобразователях, работающих в реальном времени, интервал дискретизации является обратным значением частоты дискретизации. Согласно теореме Котельникова, этот интервал определяется частотой Найквиста : чтобы представление сигнала в дискретной форме было однозначным, максимальный интервал дискретизации не должен превышать Частота дискретизации – частота взятия отсчетов непрерывного по времени сигнала при его дискретизации. Измеряется в герцах. Fд = 1/Tд = 2Fв должна быть в 2 раза больше верхней частоты спектра аналогового сигнала. Это объясняется тем, что спектр дискретизированного сигнала имеет периодический характер. Связь: Величина, обратная интервалу дискретизации называется частотой дискретизации. 4) Процесс квантования и преобразования отсчетов в двоичный код, пример. Процесс преобразования непрерывной физической величины в дискретную называется квантованием. При квантовании по уровню бесконечное множество возможных значений дискретного сигнала x(n) в заданном максимальном диапазоне его изменения Dxmax= (xmax − xmin) замещается конечным числом уровней квантования m дискретного квантованного сигнала xкв(n). С одним из них в соответствии с определенным правилом или алгоритмом и отождествляется точное мгновенное значение дискретного сигнала x(n) (рис. 1.13). Интервал между уровнями квантования называется шагом квантования по уровню Q = Dxmax /m. Преобразование отсчетов непрерывного сигнала в двоичный код называется импульсно-кодовой модуляцией (ИКМ) 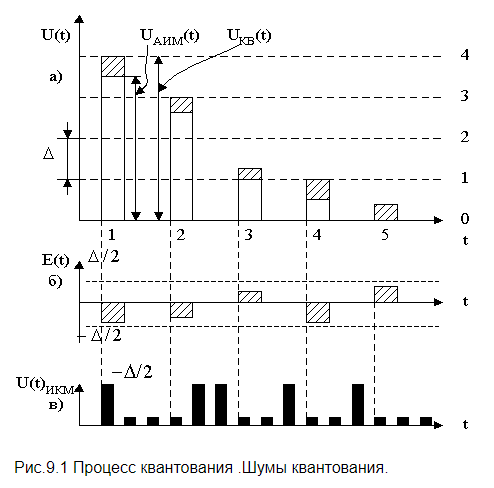 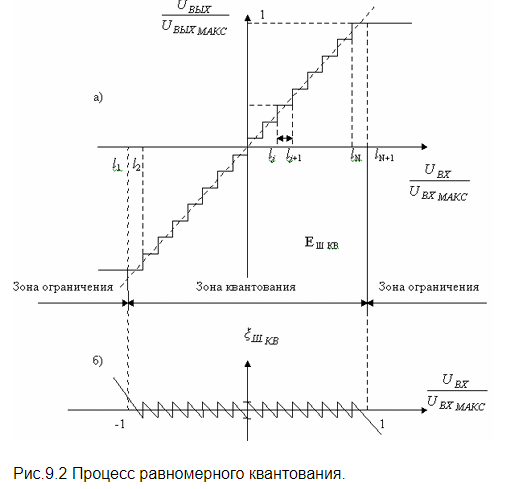 5) Связь количества уровней квантования и разрядности кодовых слов на выходе аналогово-цифрового преобразователя, пример. Количество уровней квантования определяется разрядность кодового слова. Сигнал с датчика проходит через преобразователь напряжение-частота. Таким образом на вход непосредственно логической схемы поступает сигнал, характеристикой которого является лишь частота импульсов. Логический счётчик принимает эти импульсы на вход в течение времени выборки, таким образом, выдавая к её окончанию кодовую комбинацию, численно равную количеству импульсов, пришедших на преобразователь за время выборки. 6) Понятие о нормированной частоте и основном диапазоне частот В цифровой обработке сигналов (DSP) нормализованная частота (f ') представляет собой величину, имеющую размерность частоты, выраженную в единицах "циклов на выборку". Она равна f ' = f / f s, где f - обычная частота (в "циклах в секунду"), а f s - частота дискретизации (в "выборках в секунду"). (википедия) Согласно т. Котельникова, верхняя частота fв аналогового сигнала не должна превышать половины частоты дискретизации fа этого сигнала. Следовательно, дискретные сигналы целесообразно рассматривать в области [0; fa/2], которая называется основной полосой частот или основным диапазоном частот.  Обычно предпочтение отдается абсолютной частоте f и нормированное частоте Ꞷ. Например, дискретная косинусоида в области нормированных частот имеет вид  Введение нормированной частоты указывает на то, что в ЦОС важны не абсолютные значения частот сигнала и дискретизации, а их отношение. Простейшее пример двух дискретных косинусоид:  
Z – преобразование Z-преобразованием (преобразованием Лорана) называют свёртывание исходного сигнала, заданного последовательностью вещественных чисел во временно́й области, в аналитическую функцию комплексной частоты. (Википедия на всякий случай, даже менять не буду, из учебника ниже) При исследовании дискретных сигналов и линейных систем, как правило, вместо дискретного преобразования Лапласа используют z преобразование, которое получается из дискретного преобразования Лапласa в результате замены переменных  z-преобразованием последовательности х(nТ) (2.16) называется следующий ряд: 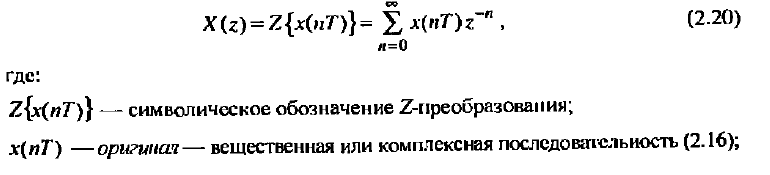 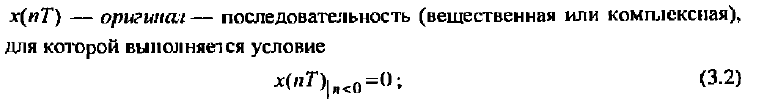 Анализ и синтез линейных дискретных систем существенно упрощается при переходе из временной области в г-область. В частности, z-преобразование позволяет ввести понятие передаточной функции в дробно- рациональном виде и описать соотношение вход-выход в виде алгебраиче- ских, а не разностных уравнений. Х(z) — z-изображение (z-образ) последовательности х(nТ), результат Z-преобразования. Область сходимости Область сходимости представляет из себя некоторое множество точек на комплексной плоскости, в которых выполнено условие см ф. 2.21 ниже. То есть сумма по членам преобразования является конечной. (Википедия) Z-преобразование однозначно связывает последовательность x(nT) с ее z-изображением Х(z) и справедливо только в области абсолютной сходимости ряда (2.20): 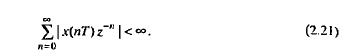 которую называют областью сходимости z-изображения. В области сходимости ряда (2.21) обеспечивается и сходимость ряда (2.20), однако обратное не всегда справедливо. Может случиться, что ряд (2.20) сходится за счет сбалансированности слагаемых с положительными и отрицательными знаками, а ряд (2.21) расходится.   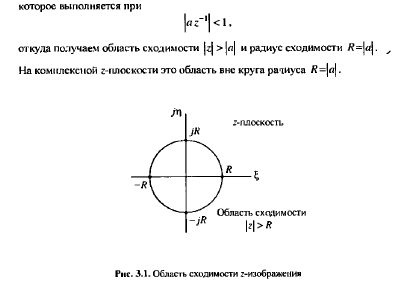 Надеюсь это идет как пример .. 3) Свойства 1. Линейность. Если последовательность х(иТ) (3.2) равна линейной комбинации последовательностей  то ее z-изображение равно линейной комбинации z-изображений данных последовательностей: 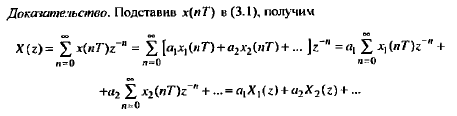  2. Z-преобразование задержанной последовательности (теорема о задержке). Z-изображение последовательности x[(n-m)T]. задержанной на (m>0) отсчетов, равно z- изображению незадержанной последовательности x(nT), умноженному на z-m : 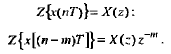  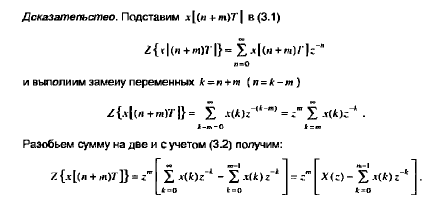 3. Z-преобразование свертки последовательностей (теорема о свертке). Сверткой последовательностей х1(nТ) и х2(nТ) называется последовательность x(nТ), определяемая соотношением:  Z-изображение свертки равно произведению z-изображений свертываемых последовательностей:  
Математическая модель АЦП как идеального амплитудно-импульсного модулятора. Математическая модель АЦП Математическую модель АЦП можно представить в виде следующей структурной схемы, изображенной на рисунке 11 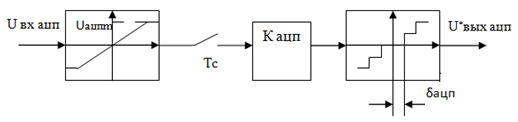 Рисунок 11 - Структурная схема АЦП На рисунке 11 имеются обозначения: Uвх ацп - максимальное входное напряжение АЦП, В; Кацп - крутизна АЦП, дацп - величина единицы младшего разряда. Рассчитаем параметры математической модели АЦП. Величина младшего разряда АЦП    Крутизна АЦП  , где Uвх ацп - максимальное входное напряжение АЦП,В; nацп - число разрядов АЦП.  Кацп = = 0,02 рад/В Математическая модель дискредитированного во времени сигнала. Математическая модель дискретизации сигналов во временной области Процесс получения отсчетов (sampling) или дискретизации сигнала можно рассматривать как умножение сигнала аналогового сигнала xa(t) на периодическую последовательность p(t) тактовых импульсов единичной амплитуды и длительностью τ, много меньшей периода отсчетов TS =T= 1 / Fs. Умножение двух сигналов – это модуляция одного сигнала другим. Поэтому процесс дискретизации можно рассматривать как амплитудно-импульсную модуляцию (АИМ). 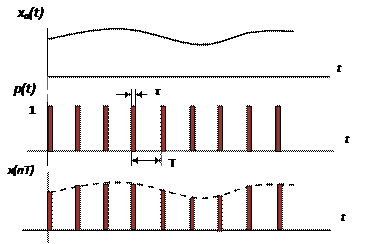 Отсчеты аналогового сигнала в равноотстоящие моменты времениt = nT образуют последовательность x[n] = xa(nT). Поскольку τ<<T, то в идеальной модели дискретизации импульсная последовательность p(t) представляется как периодическая последовательность δ – функций. 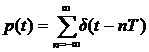  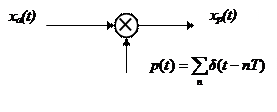 Процесс получения отсчетов (sampling) – это умножение непрерывного сигнала xa(t) на периодическую последовательность импульсов (periodic impulse train) p(t). Происходит изменение амплитуды последовательности p(t) по закону аналогового сигнала , т.е. амплитудно – импульсная модуляция (АИМ) последовательности. Результирующая последовательность xp(t) представляет собой периодическую с периодом T последовательность δ – функций с площадями, равными значениям xa(nT): 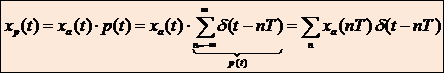 Полученное выше выражение позволяет выразить дискретный сигнал через δ – функции как функцию непрерывного времениt. Реальный дискретный сигнал отличается от идеального хотя и малой, но конечной длительностью каждого отсчета. Это связано с конечным быстродействием устройства выборки и хранения (УВХ) АЦП. Для получения такого сигнала идеальный дискретный сигнал xp(t) свертывается (операция свертки!) с реальным тактовым импульсом r(t) 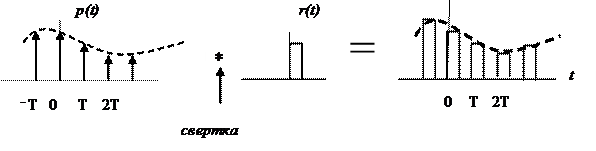 В результате свертки реальный (не идеальный) дискретный сигнал во временной области имеет вид 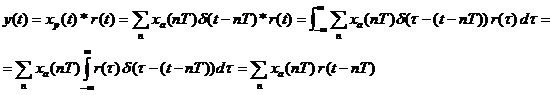 При этом r(t) – форма сигнала несущей импульсной последовательности. Результат – последовательность отсчетов – импульсов с конечной длительностью. Преобразование Лапласа и Фурье дискретизированного во времени сигнала. Формула Фурье для дискретного сигнала: 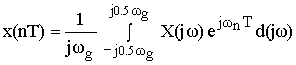 – прямое преобразование Фурье. – обратное преобразование Фурье.Сигнал x(nT) нормирован по отношению к X. После денормирования сигнала формулу записываем в виде: 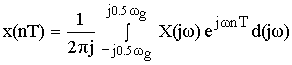 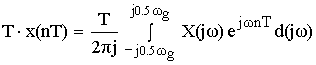  Устремляем T к нулю. Если , то T вырождается в непрерывную переменную  Денормированные формулы прямого и обратного преобразования Фурье для непрерывных сигналов: 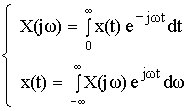 Это доказывает справедливость формулы Фурье для дискретного сигнала. Переменную ω можно распространить на всю плоскость комплексного переменного: , и тогда формулы Фурье для дискретного сигнала заменяются формулами Лапласа. 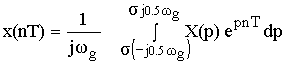 – прямое преобразование. – обратное преобразование.Интервал/период дискретизации, частота и угловая частота дискретизации. При выборе периода дискретизации можно воспользоваться теоремой В.А.Котельникова, согласно которой всякий непрерывный сигнал, имеющий ограниченный частотный спектр, полностью определяется своими дискретными значениями в моменты отсчета, отстоящие друг от друга на интервалы времени: Тд = 1/2Fmax , где Fmax – максимальная частота в частотном спектре сигнала.  УГЛОВАЯ ЧАСТОТА ДИСКРЕТИЗАЦИИ, BITCH WHAT??? бля это реально все (т – период дискретизации вродь) 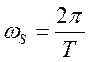 (рад/сек), еще можно записать как омега=2пи*Ф (Ф – частота)
Связь прямого Z-преобразования с дискретным преобразованием Лапласа. Связь Z-преобразования с преобразованием Лапласа найдем, записав аналоговый сигнал в виде суммы дискретных отсчетов и набора дельта-функций:  (9.13)где  шаг дискретизации. Преобразование Лапласа для такого сигнала равно: (9.14)Воспользовавшись фильтрующим свойством дельта-функции, получим:  (9.15)Сравнивая соотношения (9.1) и (9.15), замечаем, что одна формула переходит в другую при замене  . Таким образом, Z-преобразование можно получить из преобразования Лапласа путем перехода к новой переменной: (9.16)Смысл использования Z-преобразования при анализе дискретных сигналов вытекает из следующего. Так как справедливо соотношение:  , (9.17)то изменение фазовой характеристики сигнала  означает задержку сигнала на один шаг дискретизации и соответствует задержке сигнала на один такт в  области.Переход от преобразования Лапласа к Z-преобразованию при описании дискретных систем необходим по следующей причине. Дискретизация аналогового сигнала приводит к периодичности частотного спектра, то есть появлению бесконечного ряда сдвинутых копий спектра исходного непрерывного сигнала. Очевидно, эффект дискретизации приводит к появлению в плоскости  бесконечной конфигурации особых точек (полюсов и нулей), повторяющихся через интервал  .При переходе от  плоскости к  плоскости точка  отображается в точку  . Поэтому путь вдоль мнимой оси  в плоскости отображается в единичную окружность в плоскости, так как на мнимой оси  и, следовательно  Можно показать, что левая (устойчивая) полоса плоскости шириной отображается внутрь круга единичного радиуса плоскости. Все последующие полосы плоскости шириной , соответствующие периодическому частотному спектру дискретного сигнала, также отображаются внутрь круга единичного радиуса плоскости. Поэтому конфигурация особых точек (полюсов и нулей) в плоскости становится конечной.Отображение P-плоскости в Z-плоскость. 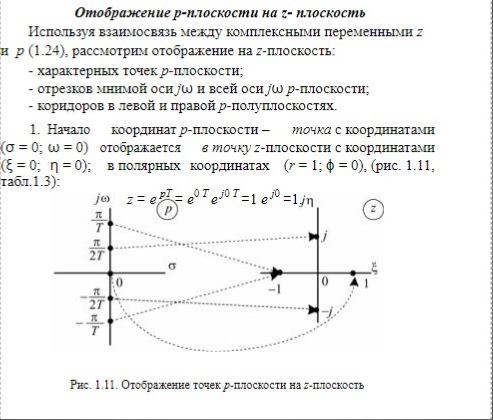   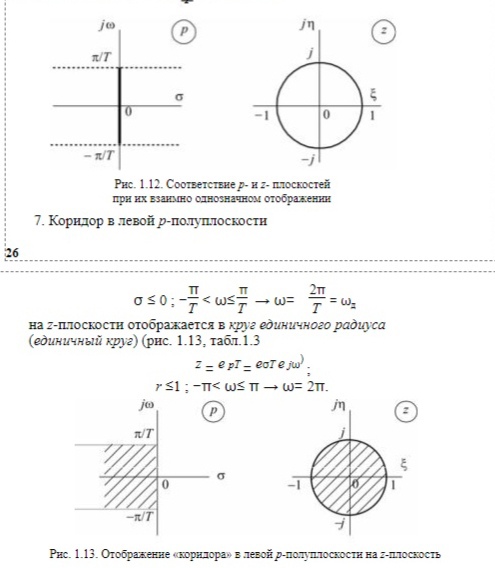  Преобразование начала координат, оси частот, левой и правой полуплоскостей из P-плоскости в Z-плоскость. (ВОТ ЭТО ХЗ)Отображение p-плоскости на z-плоскость
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
