Станки. Пример.. Университет имени Р. Е. Алексеева Кафедра Машиностроительные технологические комплексы

• Название: Университет имени Р. Е. Алексеева Кафедра Машиностроительные технологические комплексы
• Анкор: Станки
• Дата: 21.03.2022
• Размер: 1.7 Mb.
• Имя файла: Пример..doc
• Тип: Пояснительная записка; #407634
• страница: 9 из 11

3 Силовые расчеты элементов спроектированного узла

3.1 Механическая характеристика привода главного движения

Механические характеристики показывают, как изменяются мощность N и крутящий момент M с изменением частоты вращения шпинделя n.

При работе на станках целесообразно использовать привод главного движения на максимальную мощность, чтоб обеспечить наиболее эффективный (производительный) режим работы. Для универсальных станков с широким диапазоном регулирования, R_n,

установленная максимальная мощность двигателя используется полностью, начиная с некоторого номинального числа оборотов (на низких частотах трудно подобрать режим, на

котором привод работал бы с максимальной мощностью из-за возможных поломок инструмента), следовательно, для универсальных станков характерна механическая характеристика, представленная на рис. 4.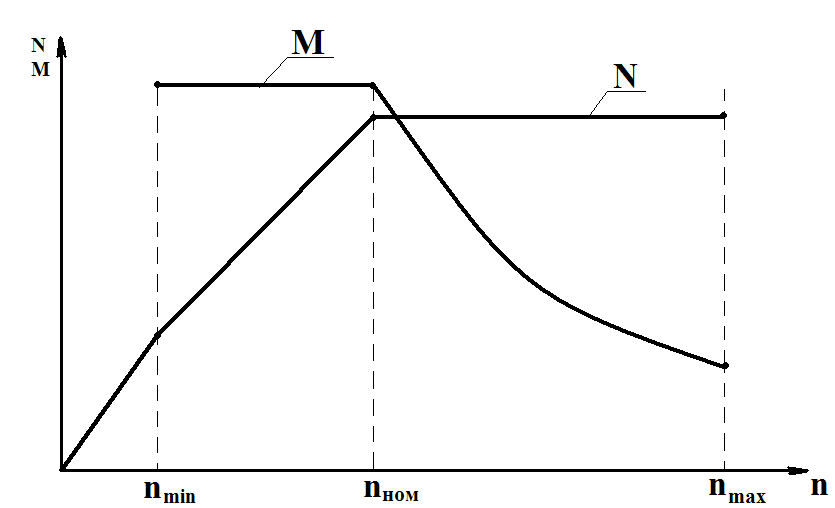


Рис. 4. Механическая характеристика универсального станка
Из рис. 4. следует, что для универсальных станков наиболее напряженным является номинальный режим работы и все дальнейшие силовые расчеты выполняем для этого режима.

Номинальную частоту вращения приблизительно можно определить по формуле:
, (3.1)

где: к – количество ступеней коробки передач, к = 18.
мин^-1

3.2 Расчет наиболее нагруженной зубчатой передачи на выносливость при изгибе

Наиболее нагруженной является передача, один из элементов которой вращается в номинальном режиме. С частотой вращения 63 мин^-1 вращается зубчатое колесо Z₂₀. С данным зубчатым колесом сопряжена шестерня Z₁₉. Следовательно, зубчатая передача U₉ c

элементами Z₁₉ – Z₂₀ является наиболее нагруженной.

Согласно расчету по формуле (3.1) номинальная частота вращения равна 63 мин^-1. С данной частотой вращается зубчатое колесо Z₂₀. Для шестерни Z₁₉ частоту вращения

определяем по структурной схеме. Итого имеем:
мин^-1;
мин^-1.

Крутящий момент на элементах зубчатой передачи определяем по формуле:
, (3.2)
где: n_эл – частота вращения шестерни или зубчатого колеса наиболее нагруженной передачи.
кгс/м
кгс/м

Определим межосевое расстояние по формуле:

мм
Определяем диаметр начальной окружности шестерни по формуле:
, (3.3)
где: U – передаточное отношение наиболее нагруженной передачи, U = U₉ = 0,25.
мм
Определяем рабочую ширину венца зубчатого колеса по формуле:
, (3.4)
где: - коэффициент ширины шестерни, = 0,3…0,6. Принимаем =0,5 мм.
мм

Усилие, действующие на единицу ширины зуба определяется по формуле:
, (3.5)
Где: К – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями по ширине зуба, К = 1,5…2. Принимаем К = 1,75.

Подставив в формулу (3.5) выражения (3.2) и (3.3) получаем формулу для определения усилия, действующего одновременно на единицу ширины зуба шестерни и зубчатого колеса:
, (3.6)
кгс/мм
Согласно формуле (3.6), усилие, действующее на единицу ширины зуба, возрастает с увеличением передаваемой мощности и передаточного числа и уменьшается с увеличением

частоты вращения, межосевого расстояния и рабочей ширины зуба. Это усилие вызывает изгиб зуба, его поломку и выкрашивание в зоне контакта.

Таким образом необходимо произвести расчет зубьев зубчатой передачи на выносливость при изгибе. Зуб рассчитываем на изгиб как консольную балку переменного сечения, нагруженную сосредоточенной силой F, определяемой по формуле:
, (3.7)

Максимальные напряжения в основании зуба определяем по формуле:

, (3.8)

где: - изгибающий момент, определяемый по формуле:
, (3.9)

- момент сопротивления сечения зуба в основании, определяемый по формуле:

, (3.10)

где: S₁ – толщина зуба в опасном сечении, мм;

- коэффициент концентрации напряжений в переходной части, .

Действие сосредоточенной силы F на зуб показано на рисунке 5.


Рис. 5 Действие сосредоточенной силы на зуб
Подставив выражения (3.9) и (3.10) в формулу (3.8) получим:
, (3.11)
Формула (3.11) также имеет следующий вид:
, (3.12)
где: - коэффициент, учитывающий форму зуба, определяемый по формуле:
, (3.13)
Величина - безразмерная величина и приблизительно равна 3,7. Подставив данное значение в формулу (3.13) имеем:
кгс/мм²
При этом должно выполняться условие выносливости при изгибе:


где: - допускаемое напряжение при изгибе, определяемое по формуле:

, (3.14)
где: S_F – коэффициент безопасности (запас прочности), S_F = 2,5;

- предел выносливости материала зебьев при пульсирующем цикле. Значение

изменяется от 40 кгс/мм² для сырых зубьев до 100 кгс/мм² для закаленных ТВЧ зубьев.

Принимаем = 100 кгс/мм²

кгс/мм²
4,6 кгс/мм² 40 кгс/мм²
Условие выносливости зубьев при изгибе выполняется.

Из формулы (3.12) видно, что напряжение изгиба в зубе возрастает с увеличением удельной окружной силы и убывает с увеличением модуля.