Теория вероятностей(ответы). Вероятность того, что расход электроэнергии на продолжении одних суток не превысит установленной нормы, равна 0,75. Найдите вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы

• Название: Вероятность того, что расход электроэнергии на продолжении одних суток не превысит установленной нормы, равна 0,75. Найдите вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы
• Дата: 04.11.2021
• Размер: 47.82 Kb.
• Имя файла: Теория вероятностей(ответы).odt
• Тип: Документы; #262808

Вероятность того, что расход электроэнергии на продолжении одних суток не превысит установленной нормы, равна 0,75. Найдите вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы
0,30

Как называют гипотезу, содержащую только одно предположение?
простой гипотезой

Дана дифференциальная функция случайной величины X: 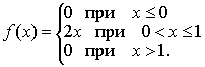  Найдите вероятность того, что в результате испытания X примет значения, принадлежащее интервалу (0,5; 1)
0,75

Как называют возможные значения r непрерывной случайной величины R, распределенной равномерно в интервале (0; 1)?
случайными числами

Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,45, во вторую — 0,35. Найдите вероятность того, что стрелок при одном выстреле попадает либо в первую, либо во вторую область
0,80

В партии из 10 деталей имеется 7 стандартных. Найдите вероятность того, что среди 4-х взятых наудачу деталей, все стандартные


В каком случае достигается минимум общих затрат задачи управления запасами в статистической детерминированной модели без дефицита?
тогда, когда затраты на создание запаса равны затратам на хранение запаса

В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: о, п, р, с, т. Найдите вероятность того, что на вынутых по одному и расположенных «в одну линию» кубиках можно будет прочесть слово «спорт»


Как называется поток событий, если его вероятностные характеристики не зависят от времени?
стационарным потоком событий

Какой из перечисленных критериев служит для проверки однородности двух независимых выборок?
критерий Вилкоксона

Какой поток событий называется простейшим (или стационарным пуассоновским)?
если он одновременно стационарен, ординарен и не имеет последействия

Что определяется с помощью обратной матрицы?
не только сам вектор оценок параметров, но и дисперсии и ковариации его элементов

Какая из перечисленных сумм вычисляется по формуле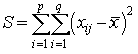 
общая сумма квадратов отклонений наблюдаемых значений от общей средней

Монета брошена 2 раза. Найдите ряд распределения случайной величины X — числа выпадения герба


Брошена игральная кость. Найдите вероятность того, что выпадет четное число очков
0,5

В ящике 5 изделий первого сорта, 10 — второго сорта и 15 — третьего сорта. Найдите вероятность того, что наугад взятое изделие — не третьего сорта
0,5

Как называется сумма произведений всех значений дискретной случайной величины X на соответствующие им вероятности?
математическим ожиданием

При каком условии вариационный ряд называется дискретным?
если любые его варианты отличаются на постоянную величину

Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение одной минуты равна 0,004. Найдите вероятность того, что в течение одной минуты обрыв произойдет в пяти веретенах
0,1562

В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найдите вероятность появления цветного шара


Какому неравенству удовлетворяет корреляционное отношение?


Что из перечисленного является мерой неопределенности случайной величины X?
энтропия

Как называется событие, состоящее в наступлении хотя бы одного из данных событий?
суммой

По какой формуле вычисляется значение приведенной интенсивности потока заявок?


Как называют случайную величину, которая служит для проверки нулевой гипотезы?
статистическим критерием

Как называют выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней?
коэффициентом вариации

В каком случае модель управления запасами является детерминированной?
если функции a(t), b(t), r(t) (соответственно интенсивности пополнения, расхода и спроса) — не случайные величины

В чем состоит метод дисперсионного анализа?
для того, чтобы проверить нулевую гипотезу о равенстве групповых средних нормальных совокупностей с одинаковыми дисперсиями, достаточно проверить по критерию F нулевую гипотезу о равенстве факторной и остаточной дисперсий

Что из перечисленного характеризует среднюю траекторию всех возможных реализаций случайного процесса?
математическое ожидание случайного процесса

Как называется событие, если в результате испытания оно обязательно должно произойти?
достоверным

Какая из перечисленных основных характеристик моделей управления запасами может быть детерминированной и случайной?
спрос

Что представляет собой закон больших чисел?
общий принцип, в силу которого совокупное действие большого числа факторов приводит при некоторых весьма общих условиях к результату, почти не зависящему от случая

Основной задачей какого анализа является переход от первоначальной системы большего числа взаимосвязанных факторов   к относительно малому числу скрытых факторов  ?
факторного анализа

В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найдите вероятность того, что в данный момент включено 4 мотора
0,246

Какой смысл имеет предельная вероятность состояния?
она показывает среднее относительное время пребывания системы в этом состоянии

В ящике имеется 50 одинаковых деталей, из них 5 окрашенных. Наудачу вынимают одну деталь. Найдите вероятность того, что извлеченная деталь окажется окрашенной
0,1

Что представляет собой относительная пропускная способность?
среднюю долю пришедших заявок, обслуживаемых системой

Как называется неслучайная функция x(t), в которую превращается случайный процесс X(t) в результате испытания?
реализацией случайного процесса

Если комбинации из n элементов отличаются только порядком расположения этих элементов, то их называют
перестановкой из n элементов

Какой считается модель управления запасами, если все параметры модели меняются во времени?
динамической моделью

Все натуральные числа от 1 до 20 записаны на одинаковых карточках и помещены в урну. После тщательного перемешивания карточек из урны взята одна карточка. Какова вероятность того, что число на взятой карточке окажется кратным 3
0,3

В каком случае модель управления запасами является стохастической?
если хотя бы одна из функций a(t), b(t), r(t) (соответственно интенсивность пополнения, расхода и спроса) носит случайных характер

Какие модели управления запасами используются, когда принимается разовое решение об уровне запасов на определенный период?
статические модели

Какое уравнение нелинейной регрессии имеет вид  ?
полиномиальное уравнение

Как называют зависимость, при которой изменение одной из величин влечет изменение распределения другой?
статистической зависимостью

Каково значение определителя неособенной матрицы?
не равен нулю

Что представляет собой процесс работы системы массового обслуживания (СМО)?
случайный процесс с дискретным состоянием и непрерывным временем

Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найдите вероятность того, что номер первого, наудачу извлеченного жетона, не содержит цифры 5
0,81

Дана интегральная функция случайной величины X: 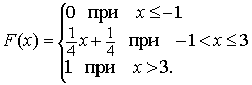  Найдите вероятность того, что в результате испытания X примет значения, принадлежащее интервалу (0; 2)


В каких моделях в качестве функции суммарных затрат, являющейся случайной величиной, рассматривают ее среднее значение или математическое ожидание?
в стохастических моделях

Чему равен выборочный коэффициент ранговой корреляции Спирмена, если между качественными признаками A и B имеется «полная прямая зависимость» в том смысле, что ранги объектов совпадают при всех значениях i?
1

Найдите математическое ожидание случайной величины X, зная ряд ее распределения: 
3,9

Как называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению  ?
гистограммой частот

Как называется отбор, при котором объекты извлекают по одному из всей генеральной совокупности?
простым случайным отбором

Как называется арифметическое значение корня квадратного из дисперсии случайного процесса?
средним квадратическим отклонением случайного процесса

Какой анализ используют в сложных случаях исследования воздействия нескольких факторов на нескольких постоянных или случайных уровнях и выяснения влияния отдельных уровней и их комбинаций?
многофакторный анализ

Какой поток не является простейшим?
регулярный поток

Какой закон распределения имеет непрерывная случайная величина X на отрезке [a, b], если ее плотность вероятности постоянна на этом отрезке и равна нулю вне его?
равномерный закон распределения

Чему равна средняя арифметическая отклонений вариантов от средней арифметической?
0

Чему равна площадь гистограммы относительных частот?
1

В чем состоит задача управления запасами в статистической детерминированной модели без дефицита?
в определении такого объема партии n, при котором суммарные затраты на создание и хранение запаса были бы минимальными

Какая из перечисленных функций представляет собой суммарные затраты на хранение и поставку запасаемого продукта и затраты на штрафы?
функция затрат

Какой из перечисленных коэффициентов вычисляется по формуле  ?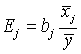
коэффициент эластичности

В каких пределах изменяется плотность убытков из-за неудовлетворенного спроса?


Какая из перечисленных формул является формулой Уильсона?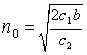


Как называют среднюю арифметическую дисперсий, взвешенную по объемам групп?
внутригрупповой дисперсией

Как называется наиболее вероятное значение случайной величины X?
модой

Как называют статистическую оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки?
несмещенной статистической оценкой

Как называется случайный процесс, если моменты возможных переходов системы из состояния в состояние не фиксированы заранее, а случайны?
процессом с непрерывным временем

Какая из перечисленных сумм характеризует влияние фактора и случайных причин?
общая сумма квадратов отклонений наблюдаемых значений от общей средней

Из перечисленных уравнений нелинейной регрессии укажите степенное


По какой формуле вычисляется значение плотности убытков из-за неудовлетворенного спроса?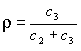


Во сколько раз оптимальный объем партии в задаче с дефицитом всегда меньше, чем в задаче без дефицита?
в   раз

Как называют совокупность объектов, из которых производится выборка?
генеральной совокупностью

Монету бросают 6 раз. Найдите вероятность того, что герб выпадет ровно 2 раза


Как называется арифметическое значение корня квадратного из дисперсии случайного процесса? 

средним квадратическим отклонением случайного процесса

ответы на "хорошо" для ТРЕНИНГА №1 по ТЕОРИИ ВЕРОЯТНОСТИ

Вероятность наступления некоторого события может быть равной:
0,6

Математическое ожидание разности двух случайных величин равна:
разности математических ожиданий этих случайных величин

Найти средний балл учащихся, которые во время экзамена получили следующие оценки:
3,7

Постоянный множитель из под знака дисперсии ...
Можно внести в квадрат и вынести

Случайная величина равномерно распределена на интервале [-2,2]. Тогда ее плотность вероятности принимает значение, равное
1/4

В партии из 10 изделий 8 изделий являются бракованными. Вероятность того, что при выборочном контроле из 5выбранных изделий бракованными окажутся 3 изделий (С - символ числа сочетаний):
2/9

Дисперсия случайной величины характеризует...
рассеивание случайной величины относительно среднего значения

Математическое ожидание случайной величины Y = 2X + 4 при M(X) = 3 равно:
10

В урне имеется 5 белых и 7 черных шаров. Из урны вынимают одновременно два шара. Вероятность того, что оба шара окажутся белыми, равна:
5/33

Дискретная случайная величина Х имеет закон распределения вероятностей (x=5;7 p=0,3;0,7):
6,4

Математическое ожидание случайной величины имеет размерность
самой случайной величины

Формула => 1-a/E
Неравенство Маркова

Формула => 1-pq/nE^2
Теорему Бернулли

Формула => 1-Q^2/E^2
Неравенство Чебышева 

Игральный кубик подбрасывают один раз. Вероятность того, что на верхней грани выпадет четное число очков, равна:
1/2

Несовместными являются следующие события?
появление валета и дамы при однократном взятии одной карты из колоды;

Дискретная случайная величина имеет закон распределения. Вероятность p3 равна::
0,3

Игральный кубик подбрасывают один раз. Событие А – “выпало число очков, большее двух”; событие В – “выпало число очков, меньшее пяти”. Верным является утверждение:
события А и В совместны

Первый студент успешно ответит на данный вариант тестов с вероятностью 0,5, а второй – с вероятностью 0,4. Вероятность того, что оба студента успешно пройдут тестирование, равна:
0,2

-----------------------------------------------------------------------
Добавлено через 46 минут
ответы на "хорошо" для КОНТРОЛЯ №1 по ТЕОРИИ ВЕРОЯТНОСТИ

В вопросах к зачету имеются 75% вопросов, на которые студенты знают ответы. Преподаватель выбирает из них два вопроса и задает их студенту. Определить вероятность того, что среди полученных студентом вопросов есть хотя бы один, на который он знает ответ
0,678

Вероятность наступления некоторого события не может быть равной:
3

Имеется 10 качественных и 4 бракованных изделий. Извлекается одно изделие. Событие А – “извлечено качественное изделие”, событие B – “извлечено бракованное изделие”. Для этих событий неверным является утверждение:
вероятность события А равна вероятности события В;

Количество комбинаций, которые можно получить путем перестановки букв, входящих в слово “число”, равно:
120

Количество различных способов выбора (порядок не имеет значения) 3 томов из 8-томного собрания сочинений равно:
56

В урне имеется а белых и b черных шаров. Из урны вынимают (одновременно или последовательно) два шара. Вероятность того, что оба шара окажутся белыми, равна:
a*(a-1)/(a+b)*(a+b-1)

Несовместными являются следующие события
появление герба и цифры при однократном подбрасывании одной монеты;

Первый стрелок попадает в мишень с вероятностью 0,9, а второй – с вероятностью 0,5. Каждый стрелок делает по одному выстрелу. Вероятность того, что оба стрелка попадут в мишень, равна:
0,45

В партии из N изделий М изделий являются бракованными. Вероятность того, что при выборочном контроле из n выбранных изделий бракованными окажутся m изделий (m< n; С - символ числа сочетаний):
верхний правый член числителя (С(N-M))^n-m

Число пятизначных чисел, одинаково читающихся слева направо и справа налево равно...
900

Если события А и В несовместны, то справедлива формула:
P(A+B)<=P(A)+P(B)

Первый студент успешно ответит на данный вариант тестов с вероятностью 0,5, а второй – с вероятностью 0,7. Вероятность того, что оба студента успешно пройдут тестирование, равна:
0,35

Сообщение от МихаилЛ  Монету бросают 6 раз. Найдите вероятность того, что герб выпадет ровно 2 раза. Ответ 15/64

Вероятность Р события А в каждом испытании постоянна, поэтому применяется формула Бернулли:
Р_m,n=C_n^m*p^m*q^n-m

здесь: n=6, m=2, p=q=0,5 

C_n^m=n!/(m!)(n-m)!) (надеюсь, n! факториал помните)

C_n^m=(1*2*3*4*5*6)/((1*2)(1*2*3*4))=15

p^m=(1/2)^2=1/4

q^n-m=(1/2)^4=1/16

Следовательно: Р_m,n=15*(1/4)*(1/16)=15/64

Ответы на "отлично" для ТРЕНИНГА и КОНТРОЛЯ №3 по ТЕОРИИ ВЕРОЯТНОСТИ

График плотности распределения вероятностей непрерывной случайной величины Х, распределенной равномерно в интервале (-2;3), имеет вид (см. рисунок). Тогда значение а равно...
0,2

Какой закон распределения имеет непрерывная случайная величина X на отрезке [a, b], если ее плотность вероятности постоянна на этом отрезке и равна нулю вне его?
равномерный закон распределения

Случайная величина равномерно распределена на интервале [0; 4]. Тогда ее плотность вероятности принимает значение, равное
1/4

Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей (1
4

График плотности распределения вероятностей случайной величины приведен на рисунке. (4/3;0,5)
1

Изизображенных на рисунке кривых линий в качестве функции распределения случайной величины с математическими ожиданием m может рассматриваться
2

График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале (-1;3), имеет вид:
0,25

Что представляет собой закон больших чисел?
общий принцип, в силу которого совокупное действие большого числа факторов приводит при некоторых весьма общих условиях к результату, почти не зависящему от случая

Формула => 1-a/E
Неравенство Маркова

Формула => 1-pq/nE^2
Теорему Бернулли

Формула => 1-Q^2/E^2
Неравенство Чебышева 

График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале (-1;5), имеет вид:
1/6

Дана плотность вероятности непрерывной случайной величины X, 
Найдите вероятность того, что в результате испытания X примет значения, принадлежащее интервалу (0,5;1)
0,75

Непрерывная случайная величина Х задана дифференциальной функцией распределения вероятностей (0
1/9

Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей (1
0

На рисунке изображены четыре кривые, характеризующие случайные величины с гауссовскими плотностями вероятности и одинаковыми математическими ожиданиями, равными m. Наибольшее значение дисперсии соответствует кривой:
4

П.С. ---------------------------------
Чтобы пройти ИТОГОВОЕ тестирование по ТЕОРИИ ВЕРОЯТНОСТИ на "хорошо" достаточно тех ответов что я выложил в своих двух постах в этой теме

Есть 4 ошибки по 2 части, но для тебя хоть что-то:
Дискретная случайная величина имеет закон распределения:
Вероятность равна:
X 2 4 7 11
P 0,1 0,2 P3 0,5

0,3 

Найти медиану для заданного ряда оценок, полученных учащимися на экзамене:
5; 4; 4; 5; 3; 2; 3; 5; 5
4

Найти моду для заданного ряда оценок, полученных учащимися на экзамене:
5; 4; 4; 5; 3; 2; 3; 5; 5
5

Математическое ожидание случайной величины Y = 5 X - 3 при M(X) = 2 равно:
7

Дано следующее распределение дискретной случайной величины Х
X 1 2 4 5
P 0.31 0.1 0.29 0.3 
Найти ее математическое ожидание, дисперсию и среднеквадратичное отклонение, используя формулы для их определения
М(х) = 3,17; Д(х) = 2,80; 

Математическое ожидание случайной величины характеризует...
среднее значение случайной величины 

Дискретная случайная величина задана законом распределения вероятностей, тогда ее математическое ожидание равно 1,7, если ...
X -2 1 3
P 0,1 a b

a=0,4, b=0,5 

Найти средний балл учащихся, которые во время экзамена получили следующие оценки:
5; 4; 4; 5; 3; 2; 3; 5; 5
4

Как называется сумма произведений всех значений дискретной случайной величины X на соответствующие им вероятности?
Математическим ожиданием 

Дисперсия случайной величины имеет размерность
квадрата случайной величины 

Как называется наиболее вероятное значение случайной величины X?
Модой

Дискретная случайная величина Х имеет закон распределения вероятностей:
Х 2 4
P 0,2 0,8
Математическое ожидание M(X) этой случайной величины равно:
3,6

Дисперсия разности двух независимых случайных величин равна:
сумме дисперсий этих случайных величин 

Функция распределения случайной величины определяется как:
вероятность попадания случайной величины в заданный интервал 

Постоянный множитель из под знака математического ожидания ...
Можно внести в квадрат и вынести 

Ряд распределения дискретной случайной величины характеризует:
только возможные значения случайной величины

Вот ещё правильные ответы, что есть по ТЕОРИИ ВЕРОЯТНОСТЕЙ:

Если события А и В несовместны, то справедлива формула:
P(A+B)=P(A)+P(B)

Дана плотность вероятности непрерывной случайной величины X: … Найдите вероятность того, что в результате испытания X примет значения, принадлежащее интервалу (0,3;1)
0,91

Непрерывная случайная величина Х задана дифференциальной функцией распределения вероятностей F(x)=
0, x<=-1
Cx^2, -10, x>2
Тогда значение С равно ... Выберите один ответ:
1/3

Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей F(x)=
0, x<=2
Cx-a, 21, x>4
Тогда значение С равно ... Выберите один ответ:
C=1/2, a=1

Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей F(x)=
C, x<=2
3x-6, 21, x>7/3
Тогда значение С равно
0

Вероятность для студента сдать первый экзамен равна 0,6, второй — 0,4. Вероятность сдать либо первый, либо второй, либо оба экзамена равна:
0,76

Вероятность изготовления нестандартной детали равна 0,11. Пользуясь формулой Бернулли найти вероятность того, что из пяти наудачу взятых деталей будут четыре стандартных.
0,345

Игральный кубик подбрасывают 1 раз. Вероятность того, что на верхней грани выпадет число очков, равное 2 или 4, равна...
1/3

Если события А и В совместны, то справедлива формула:
ответ: P(A+B)≤P(A)+P(B)

Игральный кубик подбрасывают один раз. Вероятность того, что на верхней грани выпадет число очков, равное двум или четырем, равна:
ответ: 1/3

Игральный кубик подбрасывают один раз. Событие А – “выпало число очков, большее трех”; событие В – “выпало число очков, меньшее трех”. Верным является утверждение:

события А и В несовместны

1 модуль, 2 модуль, 3 модуль и итоговое тестирование.
В итоговом тестировании вопросы практически не совпадали с теми, которые были в модулях, поэтому пришлось немного "попотеть".
Все ответы верные (все на 100%)

МОДУЛЬ 1

Вероятность наступления некоторого события не может быть равной:
Ответ – 3 

Число пятизначных чисел, одинаково читающихся слева направо и справа налево равно... 
Ответ – 900 

Количество комбинаций, которые можно получить путем перестановки букв, входящих в слово “число”, равно:
Ответ – 120 

Игральный кубик подбрасывают один раз. Вероятность того, что на верхней грани выпадет число очков, равное двум или четырем, равна:
Ответ – 1/3 

Количество различных способов выбора (порядок не имеет значения) 3 томов из 8-томного собрания сочинений равно:
Ответ – 56 

Игральный кубик подбрасывают один раз. Событие А – “выпало число очков, большее трех”; событие В – “выпало число очков, меньшее трех”. Верным является утверждение:
Ответ – события А и В несовместны 

Несовместными являются следующие события
Ответ – появление герба и цифры при однократном подбрасывании одной монеты; 

Первый студент успешно ответит на данный вариант тестов с вероятностью 0,5, а второй – с вероятностью 0,7. Вероятность того, что оба студента успешно пройдут тестирование, равна:
Ответ – 0,35 

В урне имеется а белых и b черных шаров. Из урны вынимают (одновременно или последовательно) два шара. Вероятность того, что оба шара окажутся белыми, равна:
Ответ – (а*(а-1))/((а+б)*(а+б-1)) 

Вероятность изготовления нестандартной детали равна 0,11. Пользуясь формулой Бернулли найти вероятность того, что из пяти наудачу взятых деталей будут четыре стандартных.
Ответ – 0,345 

Вероятность для студента сдать первый экзамен равна 0,6, второй — 0,4. Вероятность сдать либо первый, либо второй, либо оба экзамена равна:
Ответ – 0,76 

Имеется 10 качественных и 4 бракованных изделий. Извлекается одно изделие. Событие А – “извлечено качественное изделие”, событие B – “извлечено бракованное изделие”. Для этих событий неверным является утверждение:
Ответ – вероятность события А равна вероятности события В 

Первый стрелок попадает в мишень с вероятностью 0,9, а второй – с вероятностью 0,5. Каждый стрелок делает по одному выстрелу. Вероятность того, что оба стрелка попадут в мишень, равна:
Ответ – 0,45 

Если события А и В совместны, то справедлива формула:
Ответ – Р(А+В)<=Р(А)+Р(В) 

В вопросах к зачету имеются 75% вопросов, на которые студенты знают ответы. Преподаватель выбирает из них два вопроса и задает их студенту. Определить вероятность того, что среди полученных студентом вопросов есть хотя бы один, на который он знает ответ
Ответ – 0,938 

В партии из N изделий М изделий являются бракованными. Вероятность того, что при выборочном контроле из nвыбранных изделий бракованными окажутся m изделий (m< n; С - символ числа сочетаний):
Ответ – (СmM*C(n-m)(N-M))/(CnN) 


МОДУЛЬ 2

Дисперсия случайной величины имеет размерность
Ответ – квадрата случайной величины 

Дано следующее распределение дискретной случайной величины Х
Х 1 2 4 5
Р 0.31 0.1 0.29 0.3
Найти ее математическое ожидание, дисперсию и среднеквадратичное отклонение, используя формулы для их определения.
Ответ – М(х) = 3,17; Д(х) = 2,80; 

Найти медиану для заданного ряда оценок, полученных учащимися на экзамене:
5; 4; 4; 5; 3; 2; 3; 5; 5
Ответ – 4 

Найти средний балл учащихся, которые во время экзамена получили следующие оценки:
5; 4; 4; 5; 3; 2; 3; 5; 5
Ответ – 4 

Как называется наиболее вероятное значение случайной величины X?
Ответ – Модой 

Как называется сумма произведений всех значений дискретной случайной величины X на соответствующие им вероятности?
Ответ – Математическим ожиданием 

Функция распределения случайной величины определяется как:
Ответ – вероятность попадания случайной величины в область левее (менее) заданного значения 

Дискретная случайная величина Х имеет закон распределения вероятностей:
Х 2 4
Р 0,2 0,8
Математическое ожидание M(X) этой случайной величины равно:
Ответ – 3,6 

Дискретная случайная величина Х имеет закон распределения:
Х 2 4 7 11
Р 0,1 0,2 Р3 0,5
Вероятность Р3 равна:
Ответ – 0,2 

Дисперсия разности двух независимых случайных величин равна:
Ответ – сумме дисперсий этих случайных величин 

Математическое ожидание случайной величины характеризует...
Ответ – среднее значение случайной величины 

Математическое ожидание М(Y) случайной величины Y=5X-3 при М(Х)=2 равно:
Ответ – 7 

Найти моду для заданного ряда оценок, полученных учащимися на экзамене:
5; 4; 4; 5; 3; 2; 3; 5; 5
Ответ – 5 

Постоянный множитель из под знака математического ожидания ...
Ответ – Можно вынести 

Ряд распределения дискретной случайной величины характеризует:
Ответ – соответствие между значениями случайной величины и их вероятностями 

Дискретная случайная величина задана законом распределения вероятностей, тогда ее математическое ожидание равно 1,7, если ...
Х -2 1 3
З 0,1 а б
Ответ – a=0,4, b=0,5 


МОДУЛЬ 3

Формула Р(|Х-а|<=е)>=1-б2/е2 выражает
Ответ – Неравенство Чебышева 

Дана плотность вероятности непрерывной случайной величины X:
f(х)= 0 при х<=0
2х при 0<х<=1
0 при х>1
Найдите вероятность того, что в результате испытания X примет значения, принадлежащее интервалу (0,5;1)
Ответ – 0,75 

Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей
F(x)= 0, х<=1
Сх-4, 1<х<=1,25
1, х>1,25
Тогда значение С равно ...
Ответ – 4 

График плотности распределения вероятностей непрерывной случайной величины Х, распределенной равномерно в интервале (-2;3), имеет вид (см. рисунок). Тогда значение а равно...
Ответ – 0,2 

На рисунке изображены четыре кривые, характеризующие случайные величины с гауссовскими плотностями вероятности р(х) и одинаковыми математическими ожиданиями, равными m. Наибольшее значение дисперсии соответствует кривой:
Ответ – 4 

Что представляет собой закон больших чисел?
Ответ – общий принцип, в силу которого совокупное действие большого числа факторов приводит при некоторых весьма общих условиях к результату, почти не зависящему от случая 

Случайная величина равномерно распределена на интервале [0; 4]. Тогда ее плотность вероятности принимает значение, равное
Ответ – 1/4 

График плотности распределения вероятностей f(x) случайной величины приведен на рисунке. (4/3 0,5)
Тогда значение а равно ...
Ответ – 1 

График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале (-1;3), имеет вид:
Тогда значение а равно...
Ответ – 0,25 

Какой закон распределения имеет непрерывная случайная величина X на отрезке [a, b], если ее плотность вероятности постоянна на этом отрезке и равна нулю вне его?
Ответ – равномерный закон распределения 

Формула Р(Х<=е)>=1-а/е выражает
Ответ – Неравенство Маркова 

Из изображенных на рисунке кривых линий F(x) в качестве функции распределения случайной величины с математическими ожиданием m может рассматриваться
Ответ – 2 

Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей
F(x)= C, x<=1
5x-5, 1
1, x>1,2
Тогда значение С равно …
Ответ – 0 

Непрерывная случайная величина Х задана дифференциальной функцией распределения вероятностей
f(x)= 0, x<=0
Cx2, 0
0, x>3
Тогда значение С равно ...
Ответ – 1/9 

График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале (-1;5), имеет вид:
Тогда значение a равно...
Ответ – 1/6 

Формула Р(|m/n -p|<=е)>=1- pq/ne2 выражает
Ответ – Теорему Бернулли 


ИТОГОВОЕ ЗАДАНИЕ

В урне имеется 5 белых и 7 черных шаров. Из урны вынимают одновременно два шара. Вероятность того, что оба шара окажутся белыми, равна:
Ответ – 5/33 

Математическое ожидание случайной величины имеет размерность
Ответ – самой случайной величины 

Непрерывная случайная величина Х задана дифференциальной функцией распределения вероятностей
F(x)= 0, x<=-1
Cx2, -1
0, x>2
Тогда значение С равно …
Ответ – 1/3 

Дисперсия случайной величины характеризует...
Ответ – рассеивание случайной величины относительно среднего значения 

Случайная величина равномерно распределена на интервале [-2,2]. Тогда ее плотность вероятности принимает значение, равное
Ответ – ¼ 

Дискретная случайная величина X имеет закон распределения:
Вероятность p3 равна:
X 7 14 21 28
P 0,1 0,2 р3 0,4
Ответ – 0,3 

Игральный кубик подбрасывают один раз. Событие А – “выпало число очков, большее двух”; событие В – “выпало число очков, меньшее пяти”. Верным является утверждение:
Ответ – события А и В совместны 

Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей
F(x)= C, x<=2
3x-6, 2
1, x>7/3
Тогда значения С и а равны …
Ответ – 0 

Найти средний балл учащихся, которые во время экзамена получили следующие оценки:
5; 3; 4; 5; 3; 2; 3; 5; 4; 3
Ответ – 3,7 

Если события А и В несовместны, то справедлива формула:
Ответ – P(A+B)=P(A)+P(B) 

В партии из 10 изделий 8 изделий являются бракованными. Вероятность того, что при выборочном контроле из 5 выбранных изделий бракованными окажутся 3 изделий (С - символ числа сочетаний):
Ответ – 2/9 

Первый студент успешно ответит на данный вариант тестов с вероятностью 0,5, а второй – с вероятностью 0,4. Вероятность того, что оба студента успешно пройдут тестирование, равна:
Ответ – 0,2 

Математическое ожидание разности двух случайных величин равна:
Ответ – разности математических ожиданий этих случайных величин 

Математическое ожидание M (Y) случайной величины Y = 2X + 4 при M (X) = 3 равно:
Ответ – 10 

Вероятность наступления некоторого события может быть равной:
Ответ – 0,6 

Дискретная случайная величина Х имеет закон распределения вероятностей:
X 5 7
P 0,3 0,7
Математическое ожидание M(X) этой случайной величины равно:
Ответ – 6,4 

Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей
F(x)= 0, x<=2
Cx-a, 2
1, x>4
Тогда значения С и а равны …
Ответ – С = 1/2, а = 1 

Постоянный множитель из под знака дисперсии ...
Ответ – Можно внести в квадрат и вынести 

Игральный кубик подбрасывают один раз. Вероятность того, что на верхней грани выпадет четное число очков, равна:
Ответ – ½ 

Несовместными являются следующие события
Ответ – появление валета и дамы при однократном взятии одной карты из колоды; 

Дана плотность вероятности непрерывной случайной величины X:
f(х)= 0 при х<=0
2х при 0<х<=1
0 при х>1
Найдите вероятность того, что в результате испытания X примет значения, принадлежащее интервалу (0,3;1)
Ответ – 0,91