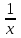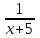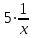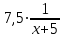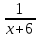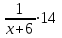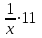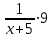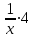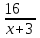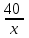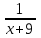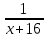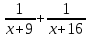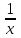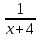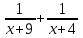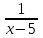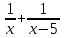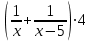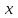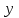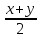1 Текстовые задачи_Новиков. Вычисления Задание 1
 Скачать 0.51 Mb.
|
|
Пример 7. Бассейн наполняется через первую трубу на 5 часов быстрее, чем через вторую. Бассейн можно наполнить, если открыть сначала одну первую трубу на 5 часов, а затем одну вторую на 7,5 часа. За сколько часов наполнится бассейн при совместной работе обеих труб? ▼ Пусть х – время заполнения бассейна первой трубой. Строим таблицу:
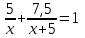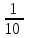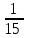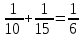Составляем уравнение  х = 10;-2,5.Таким образом, первая труба заполняет бассейн за 10 часов и ее производительность равна  ; вторая труба заполняет бассейн за 15 часов и ее производительность равна ; их совместная производительность составляет  . Следовательно, две трубы наполняют бассейн при совместной работе за 6часов.Ответ: 6.▲ Задание 1. Два каменщика выложили стену за 14 дней, причем второй присоединился к первому через 3 дня после начала работы. Известно, что первому каменщику на выполнение всей работы потребовалось бы на 6 дней больше, чем второму. За сколько дней мог бы выложить эту стену каждый каменщик, работая отдельно? ▼ Пусть х – время выполнения всей работы вторым каменщиком. Строим таблицу:
Составляем уравнение 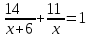 х = 22;-7.Таким образом, второй каменщик выполнит всю работу за 22 дня, первый – за 28 дней. Ответ: 28; 22▲ Задание 2. На строительстве стены первый каменщик работал 5 дней один. Затем к нему присоединился второй каменщик, и они вместе закончили работу за 4 дня. Известно, что первому каменщику потребовалось бы на выполнения этой работы на 5 дней больше, чем второму. За сколько дней может построить эту стену первый каменщик, работая один? ▼ Пусть х – время выполнения всей работы вторым каменщиком. Строим таблицу:
Составляем уравнение 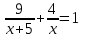 х = 10;-5.Таким образом, второй каменщик выполнит всю работу за 10 дней, первый – за 15 дней. Ответ: 15▲ Задание 3.На изготовление 16 деталей первый рабочий затрачивает на 6 часов меньше, чем второй рабочий на изготовление 40 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает второй рабочий? ▼ Примем за х – производительность второго рабочего. Строим таблицу:
Составляем уравнение 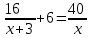 х = 5; -4.Таким образом, второй рабочий делает 5 деталей в час. Ответ: 5▲ Задание 4. Для наполнения бассейна через первую трубу потребуется на 9 часов больше времени, чем при пополнении через первую и вторую трубы, и на семь меньше, чем через одну вторую трубу. За сколько часов наполниться бассейн через обе трубы? ▼ Пусть х – время, за которое две трубы заполняют бассейн. Составляем таблицу:
Составляем уравнение 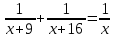 х = 12; -12.Таким образом, через 12 дней две трубы заполнят бассейн. Ответ: 12 ▲ Задание 5. Два хлопкоуборочных комбайна могут собрать хлопок с поля на 9 дней скорее, чем один первый комбайн, и на 4 дня скорее, чем один второй. За сколько дней каждый комбайн может собрать весь хлопок? ▼ Пусть х – время, за которое два комбайна смогут собрать хлопок с поля. Составляем таблицу:
Составляем уравнение 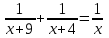 х = 6; -6.Таким образом, два комбайна соберут весь хлопок за 6 дней, первый – за 15, а второй – за 10 дней. Ответ: 15; 10 ▲ Задание 6. Два слесаря получили заказ. Сначала 1час работал первый слесарь, затем 4 часа они работали вместе. В результате было выполнено 40% заказа. За сколько часов мог выполнить заказ каждый слесарь, если первому для этого понадобилось бы на 5 часов больше, чем второму? ▼ Пусть х – время, за которое первый слесарь сможет выполнить заказ. Составляем таблицу:
Составляем уравнение 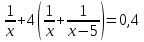 х = 2,5; 25.Таким образом, первый слесарь может выполнить заказ за 25 часов, а второй - 20 часов. Ответ: 25; 20.▲ Задание 7. За сколько часов может выполнить работу каждый из трех рабочих, если производительность труда третьего рабочего равна полусумме производительностей труда первого и второго? Известно, что если бы третий рабочий проработал один 48 часов, то для окончания работы первому требовалось бы 10 часов, а второму 15 часов. ▼ Пусть х, y – производительность первого и второго рабочего соответственно. Составляем таблицу:
Составляем систему уравнений из условий задачи: 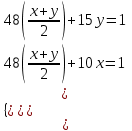 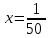 ,  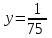, 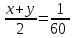- производительности каждого из рабочих.Таким образом, для выполнения работы первому рабочему потребуется 50 часов, второму – 75, третьему 60 часов. Ответ: 50; 75; 60.▲ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
