1 Текстовые задачи_Новиков. Вычисления Задание 1
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Задание 2. Один газ в сосуде А содержал 21% кислорода, второй газ в сосуде В содержал 5% кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит 14,6% кислорода. Найдите массу третьего газа. Ответ дайте в граммах. ▼ Пусть x – масса второго газа. Составляем таблицу:
Составляем уравнение 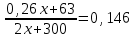 x = 600. x = 600.Таким образом, масса третьего газа равна 2х + 300 = 2∙600 + 300 =1500 г. Ответ: 1500 ▲ Задание 3. Во сколько раз больше должен быть объём 5% -го раствора кислоты, чем объём 10% -го раствора той же кислоты, чтобы при смешивании получить 7% -ый раствор? ▼ Пусть х, y – объемы соответствующих растворов. Составляем таблицу:
Составляем уравнение 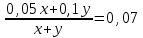 ; ; 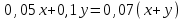 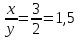 . .Таким образом, объем первого раствора должен быть больше второго в 1,5 раз. Ответ: 1,5 ▲ Задание 4. Имеются два сплава. Первый сплав содержит 10% никеля, второй 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25 % никеля. Насколько кг масса первого сплава меньше массы второго? ▼ Пусть x, y - масса первого и второго сплава соответственно. Составляем таблицу:
Составляем систему уравнений 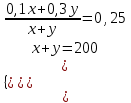 x = 50, y =150. x = 50, y =150.Таким образом, масса первого сплава меньше второго на 150 – 50 = 100 кг. Ответ: 100 ▲ Задание 5. Смешали некоторое количество 15% -го раствора некоторого вещества с таким же количеством 19% -го процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора? ▼ Пусть х - масса первого раствора. Составляем таблицу:
Составляем уравнение 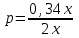 = 0,17, или 17%. = 0,17, или 17%.Таким образом, концентрация нового раствора равна 17%. Ответ: 17 ▲ Задание 6. Смешали 4 литра 15% -го водного раствора с 6 литрами 25% -го водного раствора. Сколько процентов составляет концентрация получившегося раствора? ▼ Составляем таблицу:
Концентрация получившегося раствора 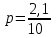 = 0,21, или 21%. = 0,21, или 21%.Ответ: 21▲ Задание 7. Имеется сплав серебра с медью. Вычислите массу сплава и процентное содержание серебра в нем, зная, что сплавив его с 3кг чистого серебра, получается сплав, содержащий 90% серебра, а сплавив его с 2 кг чистого серебра, получается сплав, содержащий 86% серебра. ▼ Пусть х, p– масса и процентное содержание серебра исходного сплава. Составляем таблицу по первому предложению:
Составляем таблицу по второму предложению:
Составляем систему уравнений 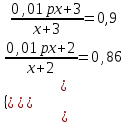 ; ; 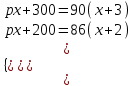 x = 0,5; р =30. x = 0,5; р =30.Таким образом, масса и процентное содержание серебра исходного сплава составляют 0,5 кг и 30% соответственно. Ответ: 0,5; 30 ▲ Задача 8. Имеются два раствора кислоты разной концентрации. Объем одного раствора 4 л, другого – 6 л. Если их слить вместе, то получится 35 % раствор кислоты. Если же слить равные объемы этих растворов, то получится 36 % раствор кислоты. Сколько литров кислоты содержится в каждом из первоначальных растворов? ▼ Пусть х, y– концентрация кислоты в первоначальных растворах. Составляем таблицу по первому предложению:
Составляем таблицу по второму предложению:
Составляем систему уравнений 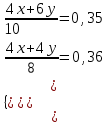 x = 0,41; y = 0,31. x = 0,41; y = 0,31.Таким образом, в первом растворе содержится 4x = 4∙0,41 = 1,64 л кислоты, а во втором – 6y = 6∙0,31 = 1,86 л. Ответ: 1,64; 1,86 ▲ Задание 9. Смешав 25%-й и 95%-й растворы кислоты и добавив 20 кг чистой воды, получили 40%-й раствор кислоты. Если бы вместо 20 кг воды добавили 20 кг 30% -го раствора той же кислоты, то получили бы 50%-й раствор кислоты. Сколько килограммов 25% -го раствора использовали для получения смеси? ▼ Пусть х, y – масса раствора с 25% -ым и 95% -ым содержанием кислоты соответственно. Составляем таблицу по первому предложению:
Составляем таблицу по второму предложению:
Составляем систему уравнений 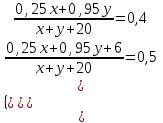 ; ; 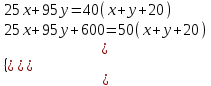 x = 20; y =30. x = 20; y =30.Таким образом, раствора с 25% -ым содержанием кислоты было 20 кг. Ответ: 20 ▲ Задание 10. Смешав 30%-й и 60%-й растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси? ▼ Пусть х, y – масса раствора с 30% -ым и 60% -ым содержанием кислоты соответственно. Составляем таблицу по первому предложению:
Составляем таблицу по второму предложению:
Составляем систему уравнений 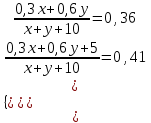 x = 60; y =30. x = 60; y =30.Таким образом, раствора с 30% -ым содержанием кислоты было 60 кг. Ответ: 60 ▲ Задание 11. Имеется три сосуда. В первый сосуд налили 4 кг 70 % сахарного сиропа, а во второй – 6 кг 40 % сахарного сиропа. Если содержимое первого сосуда смешать с содержимым третьего сосуда, то получим в смеси 55 % содержание сахара, а если содержимое второго сосуда смешать с третьим, то получим 35 % содержание сахара. Найдите массу сахарного в третьем сосуде сиропа и концентрацию сахара в нем. ▼ Пусть х, p– масса сахарного сиропа и процентное содержание сахара в третьем сосуде соответственно. Составляем таблицу
Составляем систему уравнений 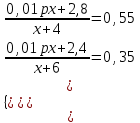 x = 1,5; p = 15. x = 1,5; p = 15.Таким образом, в третьем сосуде масса сахарного сиропа составляет 1,5 кг с содержанием сахара 15%. Ответ: 1,5; 15▲ |
