1 Текстовые задачи_Новиков. Вычисления Задание 1
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Пример 9. Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 20 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды? ▼ Пусть х – масса требуемого винограда. Составляем таблицу:
Так как масса сухого вещества не менялся, то 0,1х = 19, 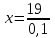 = 190. = 190.Таким образом, масса требуемого винограда составляет 190 кг. Ответ: 190 ▲ Пример 10. Свежие абрикосы содержат 80 % воды по массе, а курага (сухие абрикосы) – 12 % воды. Сколько понадобится килограммов свежих абрикосов, чтобы получить 10 кг кураги? ▼ Пусть х – масса требуемых абрикосов. Составляем таблицу:
Так как масса сухого вещества не менялся, то 0,2х = 8,8, 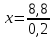 = 44. = 44.Таким образом, масса требуемых абрикосов составляет 44 кг. Ответ: 44 ▲ Пример 11. Сколько граммов воды надо добавить к 180 г сиропа, содержащего 25% сахара, чтобы получить 20%-ый сироп? ▼ Пусть х – масса требуемой воды. Составляем таблицу:
Так как масса сухого вещества (сахара) не менялся, то 0,2(х+180) = 45 х = 45. Таким образом, масса требуемой воды составляет 45 г. Ответ: 45 ▲ Пример 12. Сколько граммов воды надо выпарить из 80 г 6%-го раствора соли, чтобы получить 10%-й раствор? ▼ Пусть х – масса выпаренной воды. Составляем таблицу:
Так как масса сухого вещества (соли) не менялся, то 0,1∙(80 - х) = 4,8 х = 32. Таким образом, масса требуемой воды составляет 32 г. Ответ: 45 ▲ Пример 13. Содержание меди в первом сплаве - 10%, содержание меди во втором сплаве - 40%. Второй сплав весит на 3 кг больше первого. Сплавив первые два сплава, получили третий сплав, содержание меди в котором оказалось 30%. Вычислите массу третьего сплава. Запишите ответ в килограммах. ▼ Пусть х – масса первого сплава. Составляем таблицу:
Составляем уравнение 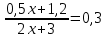 x = 3 кг. x = 3 кг.Таким образом, масса первого сплава составляет 3 кг, масса третьего сплава составляет 2х +3 = 2∙3 + 3 = 9 кг. Ответ: 9 ▲ Пример 14. Имеется 5 л 70% -го раствора серной кислоты. Сколько литров 80% -го раствора серной кислоты нужно добавить в этот раствор, чтобы получить 72%-ый раствор серной кислоты? ▼ Пусть х – искомое неизвестное. Составляем таблицу:
Составляем уравнение 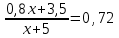 x = 1,25. x = 1,25.Таким образом, нужно добавить 1,25 л. Ответ: 1,25 ▲ Пример 15. Сплавили два слитка, содержание цинка в которых было 64% и 84% соответственно. Получили сплав, содержащий 76% цинка. Его вес 50 кг. Сколько весил каждый из сплавленных слитков? ▼ Пусть х, y – вес соответствующих слитков. Составляем таблицу:
Составляем систему уравнений 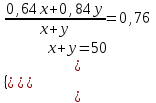 x = 20, y =30. x = 20, y =30.Таким образом, каждый из сплавленных слитков весил 20 и 30 кг соответственно. Ответ: 20; 30 ▲ Пример 16. Имеются два куска сплава меди и цинка с процентным содержанием меди 42% и 65% соответственно. В каком отношении нужно взять эти сплавы, чтобы переплавив, получить сплав, содержащий 50% меди? ▼ Пусть х, y – веса соответствующих сплавов. Составляем таблицу:
Составляем уравнение 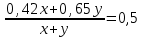 ; ; 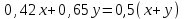 ; ;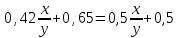 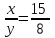 , или x:y = 15:8. , или x:y = 15:8.Таким образом, нужно взять сплавы в отношении 15:8. Ответ: 15:8 ▲ Пример 17. К 40% -му раствору соляной кислоты добавили 50 г чистой кислоты, после чего концентрация раствора стала равной 60%. Найти первоначальный вес раствора? ▼ Пусть х – первоначальный вес раствора. Составляем таблицу:
Составляем уравнение 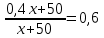 x = 100. x = 100.Таким образом, первоначальный вес раствора составляет 100 г. Ответ: 100 ▲ Пример 18. Какое количество воды надо добавить к 2 л 18% -го раствора соли, чтобы получить 16% -ый раствор ▼ Пусть х – искомое количество воды. Составляем таблицу:
Составляем уравнение 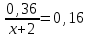 x = 0,25. x = 0,25.Таким образом, надо добавить 0,25 л воды. Ответ: 0,25 ▲ Пример 19. Один сплав содержит два метала в отношении 2:3, другой сплав содержит те же металлы в отношении 3:4. Сколько частей каждого сплава надо взять, чтобы получит третий сплав, содержащий эти металлы в отношении 15:22? ▼ Пусть х, y – веса соответствующих сплавов. Составляем таблицу:
Составляем уравнение 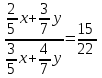 ; ; 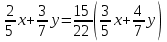 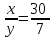 , или x:y = 30:7. , или x:y = 30:7.Таким образом, каждый металл нужно взять в отношении 30:7. Ответ: 30:7 ▲ Пример 20. Имеются три смеси (I - III), составленные из трех элементов A, B и С. В первую смесь входят только элементы А и В в весовом отношении 1:2, во вторую смесь входят только элементы В и С в весовом отношении 1:3, в третью смесь входят только элементы А и С в весовом отношении 2:1. В каком отношении нужно взять эти смеси, чтобы во вновь полученной смеси элементы А, В и С содержались в весовом отношении 11:3:8? ▼ Пусть х, y, z– веса соответствующих смесей. Составляем таблицу:
По условию задачи в полученной смеси весовые отношения А:В:С = 11:3:8, поэтому ( 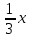 + +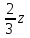 ):( ):(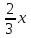 + +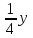 ):( ):(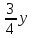 + +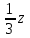 ) = 11:3:8. ) = 11:3:8.Составляем систему уравнений 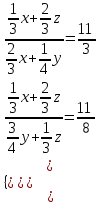 ; ; 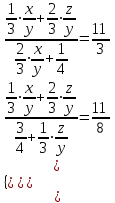 . .Обозначим 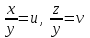 , тогда , тогда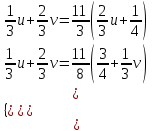 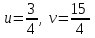 . Это означает, что . Это означает, что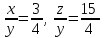 , следовательно, x:y:z=3:4:15. , следовательно, x:y:z=3:4:15.Ответ: (3:4:15). ▲ Задание 1. Сергей смешал раствор, содержащий 20% кислоты и раствор, содержащий 40% той же кислоты. В итоге у него получился раствор, содержащий 32,5% кислоты, причём объём полученного раствора 4 литра. Сколько литров раствора, содержащего 20% кислоты, использовал Сергей при смешивании? ▼ Пусть х – количество исходного раствора. Составляем таблицу:
Составляем уравнение 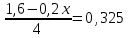 x = 1,5. x = 1,5.Таким образом, количество исходного раствора составляет 1,5 л. Ответ: 1,5 ▲ |