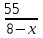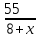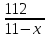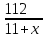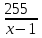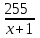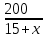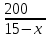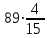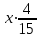1 Текстовые задачи_Новиков. Вычисления Задание 1
 Скачать 0.51 Mb.
|
|
Задание 9. Расстояние между городами А и В равно 150 км. Из города А в город В выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он вернулся в А, автомобиль прибыл в В. Найдите расстояние от А до С. Ответ дайте в километрах. ▼ Обозначим S – расстояние от A до C, v – скорость автомобиля, t – время движения мотоциклиста от A до C. По условию задачи составим таблицу.
Составляем систему уравнений 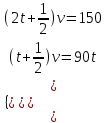 t = 1, v = 60.Тогда S = 90t = 90∙1 = 90 км. Ответ: 90.▲ Движение по воде. Если тело движется по течению реки, то его скорость относительно берега w есть сумма скорости тела в стоячей воде v и скорости течения реки u: w = v + u, при движении против течения w = v - u. Пример 1. Моторная лодка прошла против течения реки 55 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 8 км/ч. Ответ дайте в км/ч. ▼Пусть х - скорость течения реки  По условию задачи составим таблицу.
Составляем уравнение 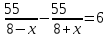 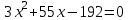 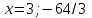 .Таким образом, скорость течения реки составляет 3 км/ч. Ответ. 3 ▲ Пример 2. Лодка шла по течению реки 2,4 ч и против течения 3,2 ч. Путь, пройденный лодкой по течению, оказался на 13,2 км длиннее пути, пройденного против течения. Найти скорость лодки в стоячей воде, если скорость течения реки равна 3,5 км/ч. ▼Пусть х - скорость лодки в стоячей воде По условию задачи составим таблицу.
Составляем уравнение 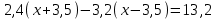 х = 8 км/ч.Таким образом, скорость лодки в стоячей воде составляет 8 км/ч. Ответ. 8 ▲ Задание 1. Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 11 км/ч. Ответ дайте в км/ч. ▼Пусть х - скорость течения реки По условию задачи составим таблицу.
Составляем уравнение 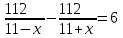 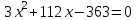 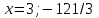 .Таким образом, скорость течения реки составляет 3 км/ч. Ответ. 3 ▲ Задание 2. Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в стоячей воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч. ▼Пусть х - скорость лодки в стоячей воде По условию задачи составим таблицу.
Составляем уравнение 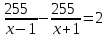 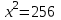 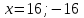 .Таким образом, скорость лодки в стоячей воде составляет 16 км/ч. Ответ. 16 ▲ Задание 3. Теплоход проходит по течению реки до пункта назначения 200 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 15 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 40 часов после отплытия из него. Ответ дайте в км/ч. ▼Пусть х - скорость течения реки По условию задачи составим таблицу.
Составляем уравнение 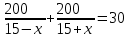  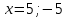 .Таким образом, скорость течения реки составляет 5 км/ч. Ответ. 5 ▲ Движение по окружности. Движение по окружности (замкнутой трассе) имеет свои особенности. 1) Пусть два тела начали движение из одной точки в одном направлении с разными скоростями, и через некоторое время один догоняет другого со спины. Чтобы один догнал другого, он должен сделать ровно на один круг больше, то есть больше на длину окружности. Если t1 – время, через которое два тела окажутся в одной точке, то tn= nt1, где tn– время, через которое они в n-й раз окажутся в одной точке. 2) Пусть два тела начали движение из одной точки в противоположном направлении с разными скоростями, и через некоторое время один встречает другого лицом. Это значит, что сумма пройденных ими расстояний равно длине замкнутой трассы (окружности). Пример 1. По окружности движутся с постоянными скоростями две точки, длина окружности 1,8 м. При движении в противоположных направлениях они встречаются через каждые 30 с. Когда они движутся в одном направлении, то одна точка догоняет другую через каждые 3 минуты. Какова скорость движения каждой точки. ▼ Пусть x, y – скорости первой и второй точки, причем x > y. Когда обе точки движутся в разных направлениях, то они обе за 30с проходят всю длину окружности, то есть 1,8 м, так как начинают движение одновременно и встречаются через каждые 30с. Составим таблицу:
Составляем первое уравнение: 30x + 30y = 1,8. Когда точки движутся в одном направлении, то первая точка догоняет вторую через каждые 3 минуты. Это означает, что за 3 минуты первая точка должна пройти полный круг 1,8 м и ещё столько, сколько успеет пройти за 3 минуты вторая точка. Составим вторую таблицу:
Составим второе уравнение: 180x – 180y = 1,8. Решаем систему уравнений: 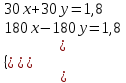 x = 0,035 м/с, y = 0,025 м/с.Ответ: 0,035; 0,025. Задание 1. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой 20 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 15 км/ч больше скорости другого? ▼ Пусть x – скорость первого мотоциклиста, а скорость второго мотоциклиста на 15 км/ч = 1/4 км/мин больше. При одновременном старте второй мотоциклист проехал на полкруга больше, т.е. на 10 км. Составляем таблицу:
Составляем уравнение 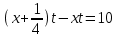 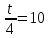 t = 40.Таким образом, мотоциклисты поравняются через 40 мин. Ответ: 40 ▲ Задача 2. Из одной точки круговой трассы, длина которой равна 8 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 89 км/ч, и через 16 мин после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч. ▼ Пусть х - скорость второго автомобиля. (16 мин = 4/15 ч). Составляем таблицу:
Составляем уравнение 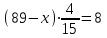 х = 59.Таким образом, скорость второго автомобиля составляет 59 км/ч. Ответ: 59 ▲ |
