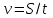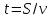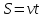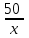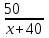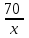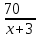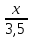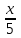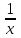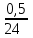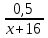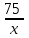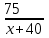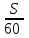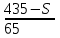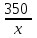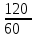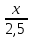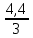1 Текстовые задачи_Новиков. Вычисления Задание 1
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Задание 29. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник? ▼ Пусть а - первоначальная стоимость акций, х – процент очередного изменения цены акции. Составляем уравнение: 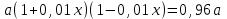 , , 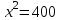 х = 20% ▲ х = 20% ▲Задачи на числа Задание 1. Найдите двузначное число, если частное от деления искомого числа на сумму его цифр равна 4, а частное от деления произведения его цифр на сумму цифр равно 2. ▼ Представим искомое число в виде 10y + x, где x – цифра единиц, y – цифра десятков. Составляем систему уравнений 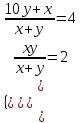 , , 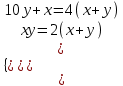 x = 6, y = 3. x = 6, y = 3.Искомое число 10y + x = 10∙3 + 6 = 36 ▲ Задание 2. Найдите двузначное число, если произведение его цифр в 6 раз меньше самого числа, а если к исходному числу прибавить 9, то получится число, написанное теми же цифрами, но в обратном порядке. ▼ Представим искомое число в виде 10y + x, где x – цифра единиц, y – цифра десятков. Составляем систему уравнений 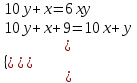 , , 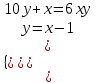 x = 2, y = 1. x = 2, y = 1.Искомое число 10y + x = 10∙1 + 2 = 12 ▲ Задачи на движение Наиболее распространенный и эффективный способ решение задач на движение - использование таблиц.
Движение по прямой. Чаще всего в качестве переменной х удобнее всего выбирать скорость. Пример 1. Из пунктов A в пункт B, расстояние между которыми 50 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 4 часа позже автомобилиста. Ответ дайте в км/ч. ▼ Обозначим за х – скорость велосипедиста. По условию задачи составим таблицу.
Составляем уравнение 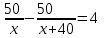 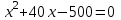 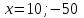 . .Таким образом, скорость велосипедиста составляет 10 км/ч. Ответ. 10▲ Пример 2. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми 70 км. На следующий день он отправился обратно со скоростью на 3км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч. ▼ Обозначим за х – скорость велосипедиста из А в В. По условию задачи составим таблицу.
Составляем уравнение 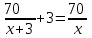 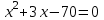 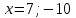 . .Таким образом, скорость велосипедиста из А в В составляет 7 км/ч. Ответ. 7 ▲ Пример 3. Первый час туристы шли на станцию со скоростью 3,5 км/ч. После этого они рассчитали, что если и дальше будут идти с той же скоростью, то придут на час позже намеченного срока. Увеличив скорость на 1,5 км/ч, туристы прибыли на станцию на 30 мин раньше намеченного срока. Какой путь прошли туристы? ▼Пусть х – путь после первого часа движения  По условию задачи составим таблицу. По условию задачи составим таблицу.
Составляем уравнение 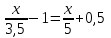 х = 17,5 км. х = 17,5 км.Путь, пройденный туристами составляет 17,5 + 3,5 = 21 км. Ответ. 21▲ Задание 1. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути – со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт B одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч. ▼ Пусть х - скорость первого автомобиля. Примем расстояние между пунктами за 1. По условию задачи составим таблицу.
Составляем уравнение 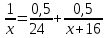 х = 32; -24. х = 32; -24.Таким образом, скорость первого автомобиля была равна 32 км/ч. Ответ. 32▲ Задание 2. Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч. ▼ Обозначим за х – скорость велосипедиста. По условию задачи составим таблицу.
Составляем уравнение 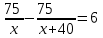 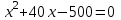 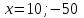 . .Таким образом, скорость велосипедиста составляет 10 км/ч. Ответ. 10▲ Задание 3. Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч? ▼ Обозначим за t – время движения автомобилей до встречи. По условию задачи составим таблицу.
Составляем уравнение 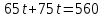 t = 4. t = 4.Таким образом, автомобили встретятся через 4 часа. Ответ: 4.▲ Задание 4. Расстояние между городами A и B равно 435 км. Из города A в город B со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся? Ответ дайте в километрах. ▼ Обозначим через S – расстояние от города А до встречи. По условию задачи составим таблицу.
Составляем уравнение 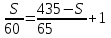 S = 240 км. S = 240 км.Ответ: 240.▲ Задание 5. Расстояние между городами A и B равно 470 км. Из города A в город B выехал первый автомобиль, а через 3 часа после этого навстречу ему из города B выехал со скоростью 60 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города A Ответ дайте в км/ч. ▼ Обозначим через x – скорость первого автомобиля. По условию задачи составим таблицу.
Составляем уравнение 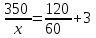 x = 70 км/ч. x = 70 км/ч.Ответ: 70.▲ Задание 6. Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. ▼ Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Пусть 3S км – весь путь автомобиля, тогда средняя скорость равна: 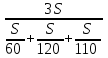 = =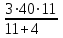 = 88 км/ч. = 88 км/ч.Ответ: 88.▲ Задание 7. Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. ▼ Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Средняя скорость автомобиля равна 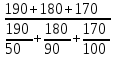 = =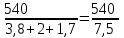 = 72 км/ч. = 72 км/ч.Ответ: 72.▲ Задание 8. Два человека отправляются из одного дома на прогулку до опушки леса, находящейся в 4,4 км от дома. Один идёт со скоростью 2,5 км/ч, а другой - со скоростью 3 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от дома произойдёт их встреча? Ответ дайте в километрах. ▼ Пусть х - искомое расстояние. По условию задачи составим таблицу.
Составляем уравнение 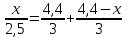 x = 4 км. x = 4 км.Ответ: 4.▲ |