1 Текстовые задачи_Новиков. Вычисления Задание 1
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Пример. Только 94% из 27 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу В1? ▼ Правильно решили задачу 27 500·0,94 = 25 850 учеников.▲ II. Нахождение числа по его процентам. Если известно, что a% числа х равно b, то число х находится по формуле 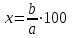 . Например, если известно, что 12% числа равно 30, то искомое число . Например, если известно, что 12% числа равно 30, то искомое число 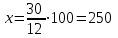 . .Пример. В школе французский язык изучают 124 учащихся, что составляет 25% от числа всех учащихся школы. Сколько учащихся в школе? ▼ Пусть х – число учащихся школы, тогда искомое число есть 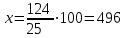 ▲ ▲Пример. Студентами технических вузов собираются стать 27 выпускников школы. Они составляют 30% от числа выпускников. Сколько в школе выпускников? ▼ Пусть х – число выпускников школы, тогда искомое число есть 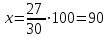 ▲ ▲III. Нахождение процентного отношения чисел. Чтобы найти процентное отношение двух чисел aи b, надо отношение этих чисел умножить на 100%, т.е. вычислить 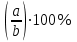 . Например, сколько процентов составляет 120 от 60: ▼ . Например, сколько процентов составляет 120 от 60: ▼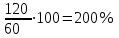 ▲ ▲В задачах часто говорится об изменении какой-либо величины на определенный процент. Что это значит? Повышение цены на 10% означает, что к прежней цене х прибавили 0,1х, т.е. новая цена составит х + 0,1х = 1,1х. Скидка на 25% означает, что прежняя цена х уменьшилась на 25%, т.е. новая цена составит х - 0,25х = 0,75х. Правило: За 100% принимаем ту величину, с которой сравниваем. Справедливы следующие утверждения: • если величину хувеличить на p%, то получим х(1 + 0,01p); • если величину хуменьшить на q%, то получим х(1 - 0,01q); • если величину хувеличить на p%, а полученный результат уменьшить на q %, то получим x(1 + 0,01p)(1 - 0,01q); • если величину хдваждыувеличить на p%, то получим х(1+ 0,01p)2; • если величину хдважды уменьшить на q%, то получим х(1- 0,01q)2; • положенная в банк под p% годовых начальная сумма S0 через n лет с учетом процентов достигнет величины Sn = S0 (1 + 0,01p)n. Задание 1. Учитель зарабатывает на 25% меньше, чем профессор. На сколько процентов больше, чем учитель, зарабатывает профессор? ▼ Если х - зарплата профессора, то х – 0,25х = 0,75х - зарплата учителя. Профессор зарабатывает больше, чем учитель на 0,25х, или 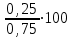 = 33,3%.▲ = 33,3%.▲Задание 2. Цена на электрический чайник была повышена на 16% и составила 3480 рублей. Сколько рублей стоил чайник до повышения цены? ▼ Пусть х – первоначальная цена чайника. Составляем уравнение: 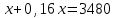 , или , или 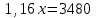 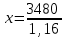 = 3000 руб. = 3000 руб.Таким образом, цена чайника до повышения составляла 3000 рублей. Ответ: 3000.▲ Задание 3. Пачка сливочного масла стоит 60 рублей. Пенсионерам магазин делает скидку 5%. Сколько рублей стоит пачка масла для пенсионера? ▼ Пачка сливочного масла для пенсионеров: 60·(1 - 0,05) = 57 руб.▲ Задание 4. Тетрадь стоит 24 рубля. Сколько рублей заплатит покупатель за 60 тетрадей, если при покупке больше 50 тетрадей магазин делает скидку 10% от стоимости всей покупки? ▼ Покупатель заплатит за 60 тетрадей со скидкой: 60·24∙(1 - 0,1) = 1296 руб.▲ Задание 5. В связи с распродажей диван подешевел на 20% и теперь стоит 12000 руб. Сколько диван стоил до распродажи? ▼ Пусть х – первоначальная цена дивана. Составляем уравнение: 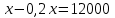 , или , или 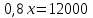 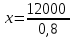 = 15000 руб. = 15000 руб.Таким образом, цена дивана до распродажи составляла 15000 рублей. Ответ: 15000.▲ Задание 6. Цена изделия составляла 1000 руб. и была снижена на 10%, а затем еще на 20%. Какова окончательная цена товара? ▼ Окончательная цена товара: 0,9∙0,8∙1000 = 0,72∙1000 = 720 руб.▲ Задание 7. Изделие, цена которого 500 руб., сначала подорожала на 10%, а затем еще на 20%. Какова окончательная цена изделия? ▼ Окончательная цена изделия: 1,1∙1,2∙500 = 1,32∙500 = 660 руб.▲ Задание 8. Цену на некоторый товар сначала снизили на 30%, а затем повысили на 20%. На сколько процентов изменилась первоначальная цена товара? ▼ Пусть х – первоначальная цена товара. Окончательная цена товара: 0,7∙1,2х = 0,84х. Первоначальная цена товара изменилась на 0,84х – х =-0,16х, т.е. снизилась на 16% ▲ Задание 9. Цену товара повысили на 25%, затем новую цену повысили еще на 10% и, наконец, после перерасчета произвели повышение еще на 12%. На сколько процентов повысилась первоначальная цена товара? ▼ Пусть х – первоначальная цена товара. Окончательная цена товара: 1,25∙1,1∙1,12х = 1,54х. Первоначальная цена товара повысилась на 1,54х – х = 0,54х, или 54% ▲ Задание 10. Цену некоторого товара снизили на 15%, потом еще на 20%. Найти общий процент снижения цены? ▼ Пусть х – первоначальная цена товара. Новая цена товара: 0,85∙0,8х = 0,68х. Изменения цены 0,68х – х =- 0,32х, т.е. общий процент снижения цены составляет 32% ▲ Задание 11. Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена цена на футболку? ▼ Изменения цены футболки равно 680 – 800 = -120, т.е. цена футболки снизилась на 120 руб., или на 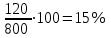 ▲ ▲Задание 12. Фрукты подешевели на 25%. Сколько фруктов можно теперь купить на те же деньги, на которые раньше покупали 3 кг? ▼ Пусть а – первоначальная цена; 3а – стоимость 3 кг фруктов по первоначальной цене; 0,75а – новая цена фруктов. По новой цене можно купить 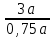 = 4 кг ▲ = 4 кг ▲Задание 13. Бананы подорожали на 10%. Сколько бананов можно теперь купить на те же деньги, на которые раньше покупали 22 кг? ▼ Пусть а – первоначальная цена; 22а – стоимость 22 кг бананов по первоначальной цене; 1,1а – новая цена бананов. По новой цене можно купить 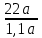 = 20 кг ▲ = 20 кг ▲Задание 14. В сентябре 1 кг винограда стоил 60 рублей, в октябре виноград подорожал на 25%, а в ноябре еще на 20%. Сколько рублей стоил 1 кг винограда после подорожания в ноябре? ▼ После подорожания в ноябре 1 кг винограда стоил 60∙1,25∙1,2 = 90 руб.▲ Задание 15. Спрос на товар увеличился в пять раз. На сколько процентов увеличился спрос? ▼ Пусть а – первоначальный спрос, который принимаем за 100%. Составляем пропорции:
Спрос увеличился на 400% ▲ Задание 16. Объем товаров увеличился на 200%. Во сколько раз произошло увеличение? ▼ Пусть а – первоначальный объем товаров, который принимаем за 100%. Составляем пропорции:
Объем товаров увеличился в 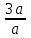 = 3 раза ▲ = 3 раза ▲Задание 17. При повышении цены билета на 25% число зрителей в кинотеатре уменьшилось на 22%. На сколько процентов изменилась выручка кинотеатра? ▼ Пусть х – первоначальная цена билета, y – количество зрителей. Имеем:
xy – выручка до повышения; 1,25x∙0,78y = 0,975xy – выручка после повышения. Выручка сократилась на 2,5% ▲ Задание 18. Цена первого товара повысилась на 30%, а потом еще на 5%. Цена второго товара повысилась на 25%. После повышения цены товаров сравнялись. На сколько процентов первоначальная цена одного товара больше первоначальной цены другого товара? ▼ Пусть х, y – первоначальные цены товаров. Составляем уравнение: 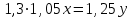 , , 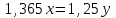 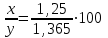 = 91,6%▲ = 91,6%▲Задание 19. Зарплата была повышена два раза за один год на один и тот же процент. При таком повышении вместо 100 рублей за один день рабочий стал получать 125, 44 руб. На сколько процентов повысилась зарплата? ▼ Пусть y – процент повышения зарплаты. Составляем уравнение: 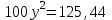 , , 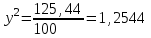 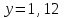 , т.е. зарплата повысилась на 12% ▲ , т.е. зарплата повысилась на 12% ▲Задание 30. Четыре одинаковые рубашки дешевле куртки на 8%. На сколько процентов пять таких же рубашек дороже куртки? ▼ Пусть x, y - стоимость одной рубашки и одной куртки соответственно. Примем стоимость одной куртки за 100%. Составляем уравнение: 4x = 0,92y. Значит стоимость одной рубашки составляет 0,92/4 = 0,23, или 23% стоимости куртки. Поэтому стоимость пяти рубашек составляет 5∙23 = 115% стоимости куртки. Это превышает стоимость куртки на 15%. ▲ Задание 31. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20 000 рублей, через два года был продан за 15 842 рублей. ▼ Пусть цена холодильника ежегодно снижалась на 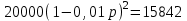 , , 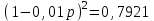 , , 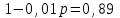 р = 11%▲ р = 11%▲Задание 32. Семья состоит из мужа, жены и их дочери-студентки. Если бы: а) зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 6,7%; б) если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены? ▼ Нарисуем таблицу
Составляем уравнения: 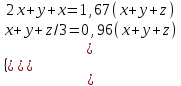 . .Вычтем из обеих частей каждого уравнения сумму (x + y + z), получим 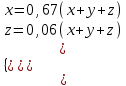 . .Это значит: а) зарплата мужа составляет 67% от общего дохода семьи; б) стипендия дочки составляет 6% от общего дохода семьи. Тогда зарплата жены составляет 100 – (67 + 6) = 27% общего дохода▲ Задание 20. Магазин в первый день продал 40% имеющихся овощей. За второй день он продал 80% овощей, проданных в первый день. В третий день – оставшиеся 28 кг. Сколько овощей было в магазине первоначально? ▼ Пусть х – вес первоначальных овощей. Составляем уравнение: 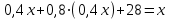 , , 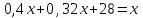 , , 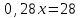 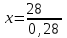 = 100 кг▲ = 100 кг▲Задание 21. Поле вспахивали в течении трех дней. В первый день вспахали 56% всей площади. Во второй - 75% остатка, а в третий – 330 га. Какова площадь поля? ▼ Пусть х – площадь поля. Составляем уравнение: 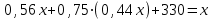 , , 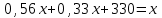 , , 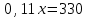 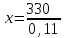 = 3000 га▲ = 3000 га▲Задание 22. Квартплата составляла 2000 руб. Какой стала квартплата после ее увеличения на 20%? ▼ Квартплата после ее увеличения на 20% составляет 1,2∙2000 = 2400 руб.▲ Задание 23. Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ? ▼ Во время распродажи шампунь станет стоить 160∙(1 − 0,25) = 120 руб. Разделим 1000 на 120: 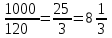 . Значит, можно будет купить 8 флаконов шампуня.▲ . Значит, можно будет купить 8 флаконов шампуня.▲Задание 24. Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%? ▼ После повышения цены ручка станет стоить 40∙(1 + 0,1) = 44 руб. Разделим 900 на 44: 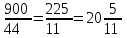 . Значит, можно будет купить 20 ручек.▲ . Значит, можно будет купить 20 ручек.▲Задание 25. Сбербанк в конце года начисляет 4% годовых к сумме, находившейся на счету в конце года. Каким станет первоначальный вклад в 2500 руб. через один год? ▼ В конце года первоначальный вклад составит 2500∙(1 + 0,04) = 2600 руб.▲ Задание 26. Сбербанк в конце года начисляет 3% годовых к сумме, находившейся на счету в начале года. На сколько рублей увеличится первоначальный вклад в 1000 руб. через два года? ▼ В конце второго года первоначальный вклад составит 1000∙(1 + 0,03)2 = 1000∙1,032 = 1000∙1,0609 = 1060,9 руб. Первоначальный капитал увеличился на 1060,9 – 1000 = 60,9 руб., или 6,09% ▲ Задание 27. Найти первоначальную сумму вклада, если после двух лет она выросла на 304,5 руб. при 3% годовых? ▼ Пусть х – первоначальная сумма вклада. Составляем уравнение: 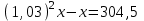 , , 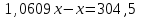 , , 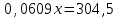 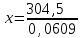 = 5000 руб.▲ = 5000 руб.▲Задание 28. Найти первоначальную сумму вклада, если после трех лет она выросла на 765,1 руб. при 2% годовых? ▼ Пусть х – первоначальная сумма вклада. Составляем уравнение: 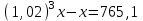 , , 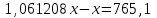 , , 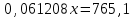 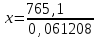 = 12500 руб.▲ = 12500 руб.▲ |

 5а – а ---- 500% - 100%
5а – а ---- 500% - 100%