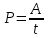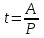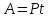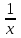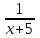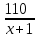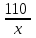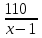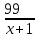1 Текстовые задачи_Новиков. Вычисления Задание 1
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Задание 3. Из пункта А круговой трассы выехал велосипедист, а через 30 мин следом за ним отправился мотоциклист. Через 10 мин после отправления он догнал велосипедиста в первый раз, а еще через 30 мин после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч. ▼ Пусть x, y – скорости велосипедиста и мотоциклиста соответственно. Первый обгон: время движения мотоциклиста 10 мин = 1/6 ч, велосипедиста – 10 + 30 = 40 мин = 2/3 ч. Составляем таблицу:
Второй обгон: Время движения мотоциклиста (велосипедиста) составляет 30 мин = 1/2 ч. Мотоциклист проехал на один круг больше, т.е. на30 км. Составим другую таблицу:
Решаем систему уравнений: 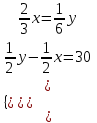 x = 20, y = 80. x = 20, y = 80.Таким образом, скорость мотоциклиста составляет 80 км/ч. Ответ: 80. Задание 4. Часы со стрелками показывают 8 ч 00 мин. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой? ▼ Скорость движения минутной стрелки 12 делений/час (под одним делением здесь подразумевается расстояние между соседними цифрами на циферблате часов), а часовой – 1 деление/час. Обозначим через t - время, за которое минутная стрелка в первый раз догонит часовую. Минутная стрелка пройдет на 2/3 круга = 8 дел. больше. Составляем таблицу:
Составляем уравнение: 12t – t = 8 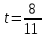 . . Значит, в первый раз стрелки поравняются через 8/11 ч. Обозначим через t - время, за которое минутная стрелка во второй раз догонит часовую. Минутная стрелка пройдет на один круг (12 дел.) больше. Составляем таблицу:
Составляем уравнение: 12t – t = 12 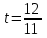 . . Итак, через 12/11 часа стрелки поравняются во второй раз, еще через 12/11 часа – в третий, и еще через 12/11 часа – в четвертый раз. Следовательно, если старт был в 8.00., то в четвертый раз стрелки поравняются через 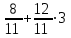 = 4 ч = 4∙60 = 240 мин. = 4 ч = 4∙60 = 240 мин.Ответ: 240▲ Задачи на работу Производительность – это объем работы, выполняемый за единицу времени (например, за час или за день). По-другому, скорость выполнения работы. Наиболее распространенный и эффективный способ решение задач на работу - использование таблиц.
Правила: • если в задаче объем работы не определяется, то весь объем работы принимается за единицу; • при совместной работе нескольких объектов их общая производительность является суммой производительности отдельных объектов. Пример 1. Один рабочий может выполнить задание на 5 часов. быстрее другого. Оба вместе они выполняют это задание за 6 часов. За сколько часов каждый из них выполнит задание? ▼ Пусть х – время выполнения задания первым рабочим. Строим таблицу:
Составляем уравнение 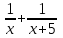 = =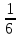 х = 10; -3. х = 10; -3.Таким образом, первый рабочий выполнит задание за 10 часов, а второй – за 15 часов. Ответ: 10; 15 ▲ Пример 2. Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше? ▼ Примем за х – производительность второго рабочего. Строим таблицу:
Составляем уравнение 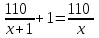 х = 10; -11. х = 10; -11.Таким образом, второй рабочий делает 10 деталей в час. Ответ: 10▲ Пример 3. Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй - за три дня? ▼ Примем всю работу за единицу. Пусть x, y – производительность первого и второго рабочего соответственно. Строим таблицу:
Составляем систему уравнений: 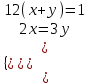 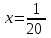 , , 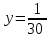 . .Итак, первый рабочий за день выполняет 1/20 всей работы. Значит, на всю работу ему понадобится 20 дней. Ответ: 20.▲ Пример 4. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 110 литров она заполняет на 1 минуту быстрее, чем первая труба? ▼ Примем за х – производительность второй трубы. Строим таблицу:
Составляем уравнение 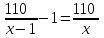 х = 11; -10. х = 11; -10.Таким образом, вторая труба пропускает 11 литров воды в минуту. Ответ: 11▲ Пример 5. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 2 минуты дольше, чем вторая труба заполняет резервуар объемом 99 литров? ▼ Пусть х - производительность первой трубы. Тогда производительность второй трубы равна х + 1. Строим таблицу:
Составляем уравнение 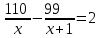 х = 10. х = 10.Таким образом, первая труба пропускает 10 литра воды в минуту. Ответ: 10▲ Пример 6. Бассейн наполняется через первую трубу на 5 часов быстрее, чем через вторую. При совместной работе обеих труб бассейн заполняется за 6 часов. За сколько часов заполнят бассейн трубы, действуя отдельно? ▼ Пусть х, y - производительность первой и второй трубы соответственно. Строим таблицу:
Составляем систему уравнений 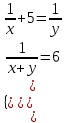 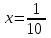 , , 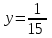 - производительности труб. - производительности труб.Таким образом, первая труба действуя отдельно наполнит бассейн за 10 часов, а вторая – за 15 часов. Ответ; 10; 15 ▲ |

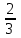
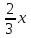
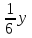
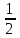
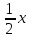
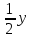 -
-