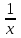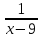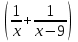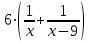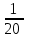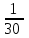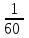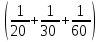1 Текстовые задачи_Новиков. Вычисления Задание 1
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Задание 8. Две бригады, работая вместе, могут выполнить работу за 6 дней. За какое время каждая бригада может выполнить эту работу, если известно, что вторая может справиться с этой работой на 9 дней быстрее, чем первая? ▼ Примем всю работу за единицу. Пусть x – время работы первой бригады. Строим таблицу:
Составляем уравнение 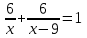 х = 18; 3. х = 18; 3.Таким образом, первая бригада может выполнить эту работу за 18 дней, а вторая – за 9 дней Ответ: 18; 9.▲ Задание 9. Двое рабочих изготавливают по одинаковому количеству деталей. Первый выполнил эту работу за 6 часов, второй за 4 часа, т.к. изготовлял в час на 14 деталей больше первого. Сколько деталей изготовил второй рабочий? ▼ Примем за х – производительность второго рабочего. Строим таблицу:
Составляем уравнение 6(x – 14) = 4x x = 42. Таким образом, второй рабочий делает 42 детали в час, а всего он изготовил 4х = 4∙42 = 168 детали. Ответ: 168▲ Задание 10. Первый насос наполняет бак за 20 минут, второй - за 30 минут, а третий - за 1 час. За сколько минут наполнят бак три насоса, работая одновременно? ▼ Примем объем бака за единицу. Строим таблицу:
Три насоса, работая вместе, заполнят бак за 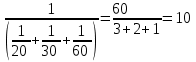 мин. мин.Ответ: 10.▲ Задачи на сплавы, смеси и растворы. Концентрация какого-то вещества в растворе - это отношение массы или объема вещества к массе или объему всего раствора. Как правило, концентрация выражается в процентах. 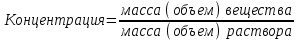 . .С математической точки зрения растворы, смеси, сплавы не отличаются друг от друга. Правила: 1) Масса раствора (смеси, сплава) равна сумме масс всех составляющих. 2) При смешивании нескольких растворов (смесей, сплавов) масса нового раствора становится равной сумме всех смешанных растворов. 3) Масса растворенного вещества при смешивании двух растворов суммируется. По вопросу задачи вводится переменная. Удобно в задачах на сплавы, смеси и растворы составлять таблицу по условию задачи, а затем заполнять пустые клетки, руководствуясь правилами и формулами расчета «Процент от числа».
Пример 1. Смешали 20 л 70% -го спирта, 30 л 50% -го спирта и 22,5 л воды. Какое процентное содержание спирта в получившейся смеси? ▼ Составляем таблицу:
Концентрация получившейся смеси 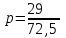 = 0,4, или 40%. = 0,4, или 40%.Ответ: 40 ▲ Пример 2. В сосуд, содержащий 5 литров 12% -го водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора? ▼ Составляем таблицу:
Концентрация получившегося раствора 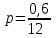 = 0,05, или 5%. = 0,05, или 5%.Ответ: 5▲ Пример 3. Сколько литров воды нужно добавить в 2 л водного раствора, содержащего 60% кислоты, чтобы получить 20% -ый раствор кислоты? ▼ Пусть х – объем добавленной воды. Составляем таблицу:
Так как объём вещества не менялся, то 0,2(x + 2) = 1,2, x = 4. Таким образом, нужно добавить 4 л воды. Ответ. 4▲ Пример 4. Мокрая губка содержала 80 % воды, а после выжимания только 20%. Чему была равна масса мокрой губки, если масса губки после выжимания стала 100 грамм? Ответ дайте в граммах. ▼ Пусть х – масса мокрой губки. Составляем таблицу:
Так как объём сухого вещества не менялся, то 0,2х = 80, 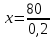 = 400. = 400.Таким образом, масса мокрой губки составляет 400 г. Ответ. 400.▲ Пример 5. Половину объёма огурца когда-то занимала вода, потом этот огурец подсох и вода стала занимать лишь 20% объёма огурца. Во сколько раз уменьшился объём этого огурца? ▼ Пусть V0, V1 – первоначальный и конечный объём огурца соответственно. Составляем таблицу:
Так как объём сухого вещества не менялся, то 0,5V0 = 0,8V1, 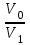 = 1,6, = 1,6,Таким образом, объём огурца уменьшился в 1,6 раз. Ответ. 1,6.▲ Пример 6. Первоначально влажность зерна составляла 25%. После того как 200 кг зерна просушили, оно потеряло в массе 30 кг. Вычислить влажность просушенного зерна. ▼ Пусть р – влажность просушенного зерна. Составляем таблицу:
Влажность просушенного зерна составляет 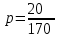 = 0,118, или 11,2%. = 0,118, или 11,2%.Ответ: 11,2 ▲ Пример 7. Влажность сухой цементной смеси на складе составляет 18%. Во время перевозки из-за дождей влажность смеси повысилась на 2%. Найдите массу привезенной смеси, если со склада было отправлено 400 кг. ▼ Пусть х - масса привезенной смеси. Составляем таблицу:
Так как масса вещества не меняется, то 0,8х = 328 х = 410. Таким образом, масса привезенной смеси составляет 410 кг. Ответ: 410 ▲ Пример 8. Сухие грибы содержат 12% воды, а свежие - 90% воды. Сколько получится сухих грибов из 22 кг свежих грибов? ▼ Пусть х – масса сухих грибов. Составляем таблицу:
Так как масса сухого вещества не менялся, то 0,88х = 2,2, 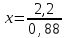 = 2,5. = 2,5.Таким образом, масса сухих грибов составляет 2,5 кг. Ответ: 2,5 ▲ |