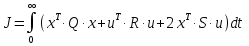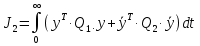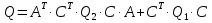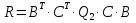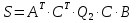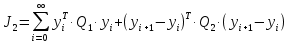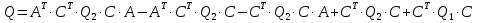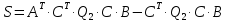Відомо, що роль нафти в сучасному світі винятково важлива, оскільки в основі всіх галузей виробництва лежить енергетика. Нафта це рідка речовина, що добувається з надр землі і використовується при виробництві палива
 Скачать 3.26 Mb. Скачать 3.26 Mb.
|
|
3.4 Розробка експериментальної лінійної математичної моделі динаміки методом активного експерименту Розробка математичної моделі може здійснюватися за допомогою можливостей Hysys, але недоліком даного способу є його орієнтація скоріше на пасивний експеримент, ніж на активний, тому графіки перехідних процесів до сталих значень не доходять через неконтрольований інтервал зміни стрибка. Тому доцільно використати наявну в Hysys модель, доповнюючи її можливостями пакета Matlab. Для обміну інформацією програм мовою Matlab з Hysys скористаємося бібліотекою для роботи з Hysys за допомогою протоколу DDE. Разом з нею необхідно використати 3 функції (Додаток В): ініціалізації (init_hysys.m), зміни параметра (setHysVar.m), одержання значення параметра (getHysVar.m). В Hysys задаємо параметри, що підлягають одержанню та передачі. Для цього створюється електронна таблиця (Spread Sheet) з параметрами каналів, що одержує автоматичне ім'я SPRDSHT-1. 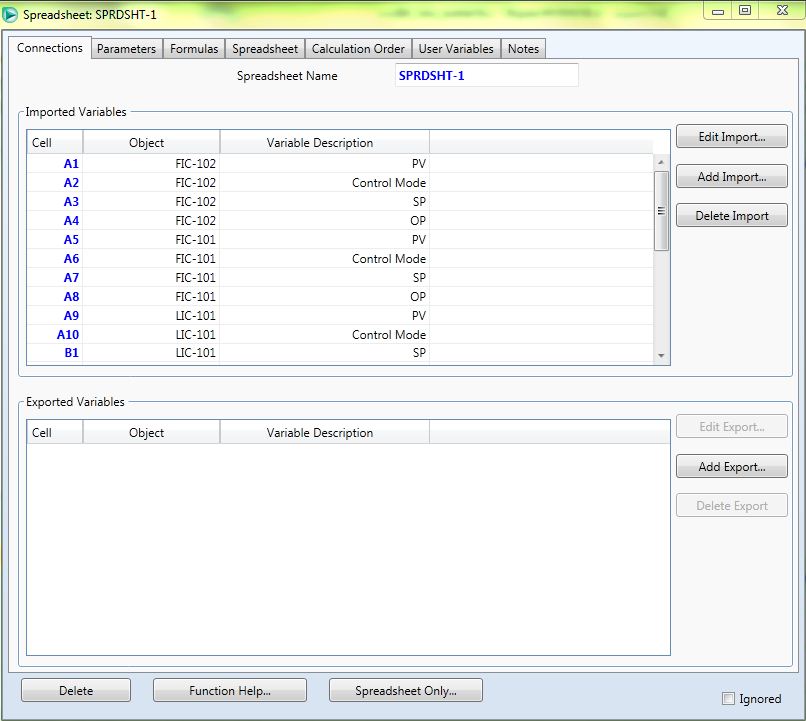 Рисунок 3.1 - Параметри, що підлягають одержанню та передачі Наведена програма (Додаток В) проводить активний експеримент та автоматично апроксимує передатні функції за допомогою функцій Identification Toolbox. Активний експеримент виконується за планом:
В результаті виконання програми одержимо графіки розгінних характеристик та апроксимовані передаточні функції (рис. 3.2 – 3.8). 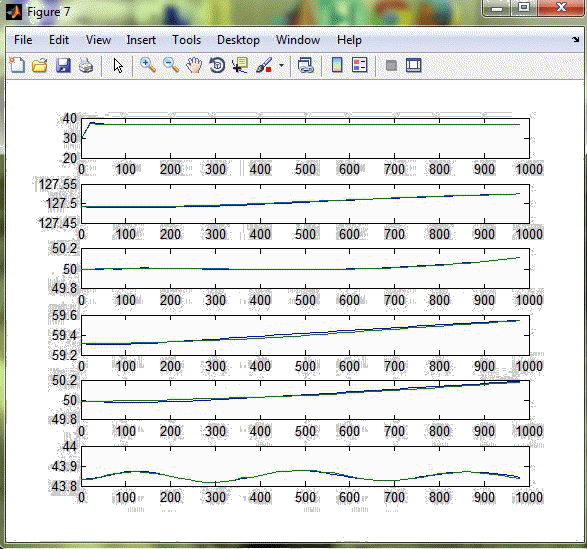 Рисунок 3.2 – Реакція каналів на стрибок 10% за витратою газойля зі стріппінгу 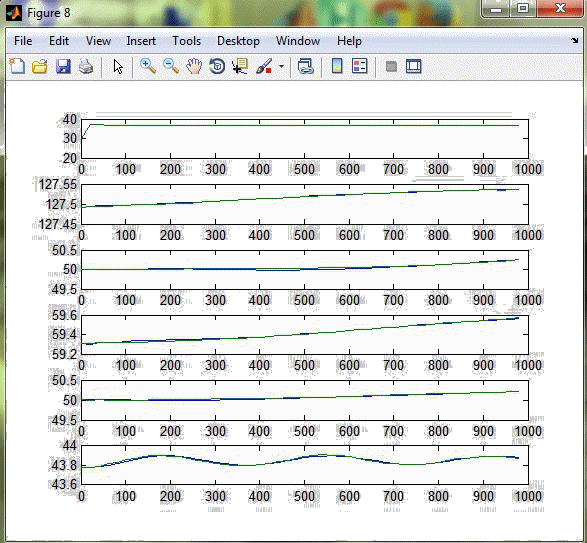 Рисунок 3.3 – Реакція каналів на стрибок 10% за витратою дизеля зі стріппінгу 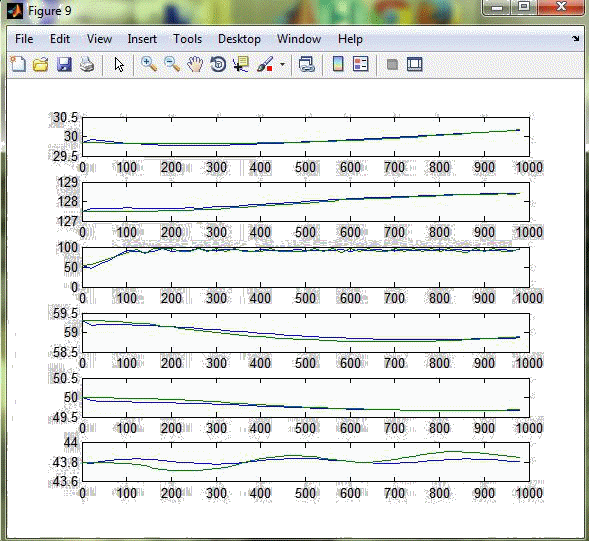 Рисунок 3.4 – Реакція каналів на стрибок 10% за рівнем гасу в ребойлері 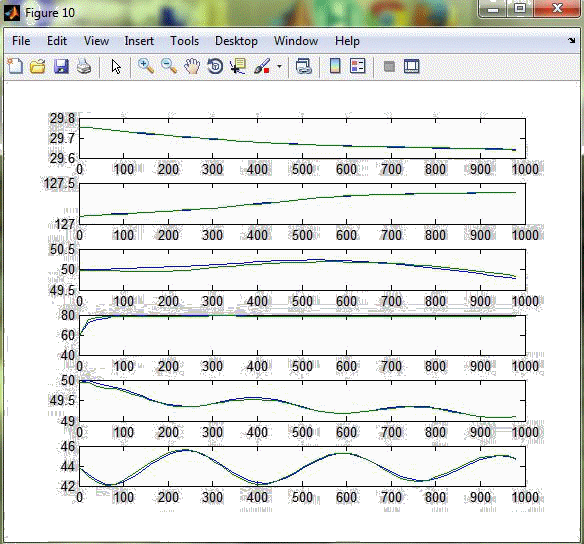 Рисунок 3.5 – Реакція каналів на стрибок 10% за температурою зрошення 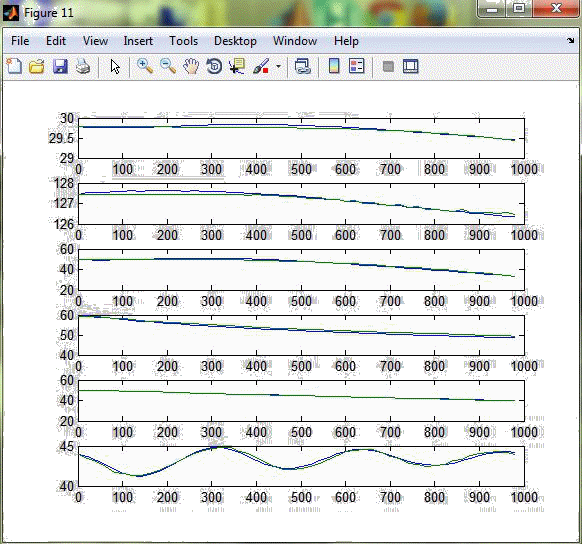 Рисунок 3.6 – Реакція каналів на стрибок 10% за рівнем в конденсаторі 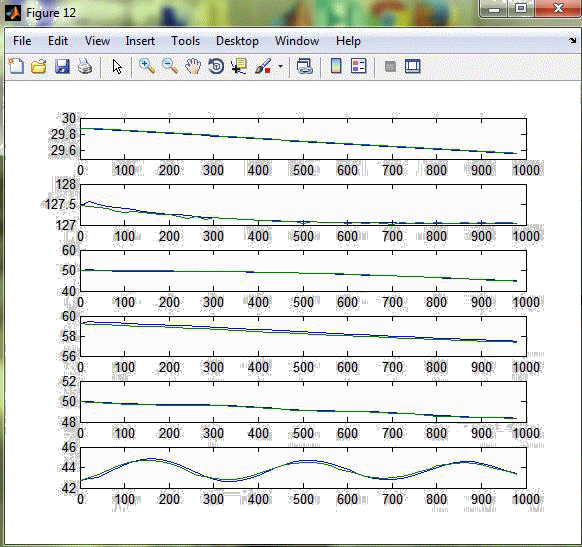 Рисунок 3.7 – Реакція каналів на стрибок 10% за температурою флегми Розгінні характеристики апроксимованих передаточних функцій високого порядку майже повністю збігаються з експериментальними розгінними характеристикам, тому можна вважати апроксимовану математичну модель адекватною. Отримані передаточні функції наведені у додатку Б.
Ректифікаційна колона – об'єкт управління зі значною інерційністю і часом запізнювання за каналами управління. При управлінні багатомірними об'єктами, класичні одномірні регулятори не забезпечують оптимальності процесів управління. Тому доцільно використати багатомірні системи управління, так як вони дають найбільш високу якість управління. Особливе значення має задача про такий вибір закону керування, щоб характеристики досягали своїх екстремальних значень з урахуванням вимоги стійкості відповідних лінійних моделей замкнутих систем. Першими конструктивними пропозиціями щодо вирішення таких завдань у нашій країні були методи аналітичного конструювання регуляторів А. М. Лєтова та методи синтезу оптимальних стабілізуючих управлінь В. І. Зубова. За кордоном дослідження по даному напрямку (LQR і LQG) були проведені Р. Калманом [36]. Структура і параметри багатомірного регулятора визначаються на основі заданих вимог до САР конкретного об'єкта управління, тому їх синтез проводиться індивідуально. Вибір алгоритму управління повинен відповідати вимогам, що пред'являються до точності і якості процесу управління САР. Чим вище ці вимоги, тим складніше алгоритм управління та регулятор. В багатомірних САР вихідна величина у є вектором і являє собою сукупність декількох вихідних змінних уi, тому багатомірна САР завжди багатоконтурна. Аналіз статики і динаміки багатомірної САР аналогічний, але більш трудомісткий порівняно з аналізом одномірної системи. Він еквівалентний випадку для одномірної САР з декількома зовнішніми впливами. Визначення точності, показників якості та побудова перехідних процесів здійснюються незалежно для кожної вихідної змінної (на основі рівнянь, передаточних функцій, частотних характеристик). [37]
На відміну від підходів класичної теорії керування, що намагається скоротити кількість розглянутих зв'язків і керованих змінних, підхід сучасної теорії керування настроєний, навпаки, на більшу деталізацію математичних моделей, що пов'язано з розвитком засобів обчислювальної техніки. Лінійно-квадратичний регулятор (англ. Linear quadratic regulator, LQR) – один із видів оптимальних регуляторів, що використовується для керування складними багатомірними і багатозв´язними об'єктами управління. Даний регулятор використовує метод подання динаміки систем у вигляді простору станів - системи лінійних ЗДР у формі Коші, записаних в матричній формі. Розглянемо алгоритм LQR-оптимального синтезу [27]. Для пошуку матриці 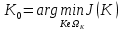 коефіцієнтів оптимального регулятора необхідно виконати наступні операції: коефіцієнтів оптимального регулятора необхідно виконати наступні операції:
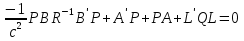 і знайти його рішення – симетричну позитивно визначену матрицю Р. 2. Побудувати матрицю коефіцієнтів 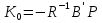 оптимального регулятора оптимального регулятора 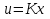 за вектором стану. за вектором стану.3. Розрахувати матричні рівняння Ляпунова: 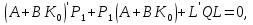 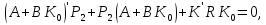 Відносно невідомих матриць Р1 і Р2. 4. Обчислити значення окремих складових інтегрального квадратичного функціоналу для замкнутої оптимальної системи, при заданому векторі початкових умов 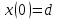 за формулами: за формулами: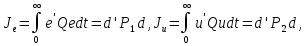 У безперервному часі критерій оптимальності лінійно-квадратичного регулятора може бути представлений у такий спосіб:
де: x – вектор змінних стану, u – вектор керуючих впливів, 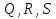 - матриці вагових коефіцієнтів. - матриці вагових коефіцієнтів.У класичній теорії керування зазвичай рекомендується критерій [9], що для систем у формі простору станів у безперервному часі може бути представлений у наступному вигляді:
Модифікуємо його, підставляючи значення похідної з рівняння системи, зведемо цей критерій до критерію J, підстановкою:
Аналогічний критерій можна записати для системи в дискретному часі:
який зводиться до критерію J у дискретному часі підстановкою:
Операції алгоритму 1 і 2 виконуються з використанням функції lqr, а 3 і 4 операції - за допомогою функції lyap, що входять до складу пакета прикладних програм СSТ середовища Мatlab. Виклик функції lqr здійснюється командою: 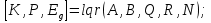 де: К – вектор з коефіцієнтами, що шукаються, Р – рішення рівняння Ріккаті, Еg – вектор з коренями характеристичного полінома замкненої системи. Якщо вхідний параметр N не заданий, він приймається нульовим. Функція lуар забезпечує розв'язок рівняння Ляпунова: 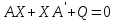 , ,а її виклик виконується в наступному форматі: 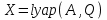 Для перевірки придатності розробленої математичної моделі високого порядку створена програма Matlab для синтезу лінійно-квадратичного П- регулятора, яка наведена у Додатку Г. В пакеті Matlab Simulink проведено математичне моделювання реакції замкнутої САР з лінійно-квадратичним регулятором, зі стандартним і модифікованим критерієм, на збурення величиною -5% х.в.м. по всіх каналах ОУ (рис. 4.3). Перехідні процеси за збуренням наведені на рис. 4.4. 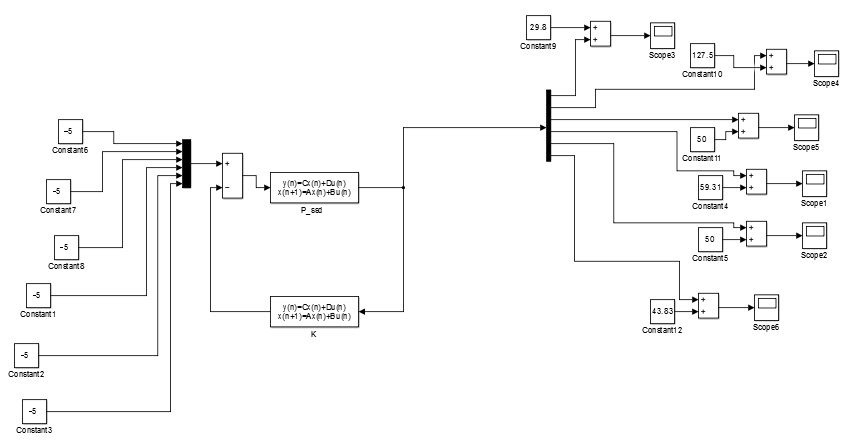 Рисунок 4.3 - Модель замкнутої системи в Simulink 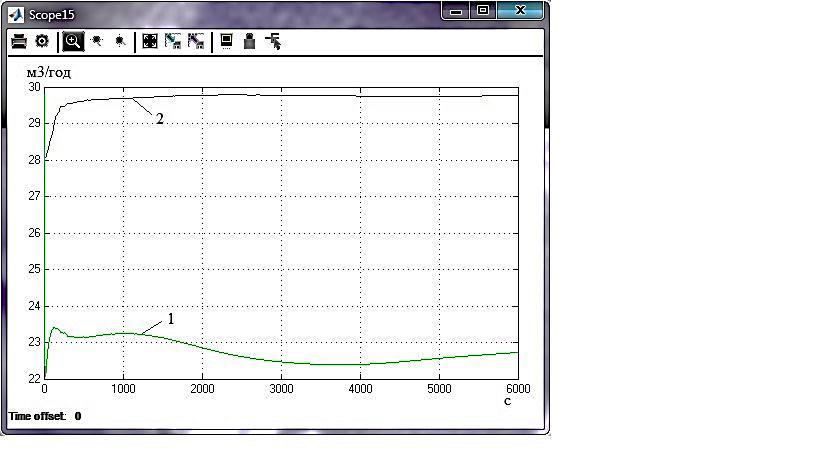 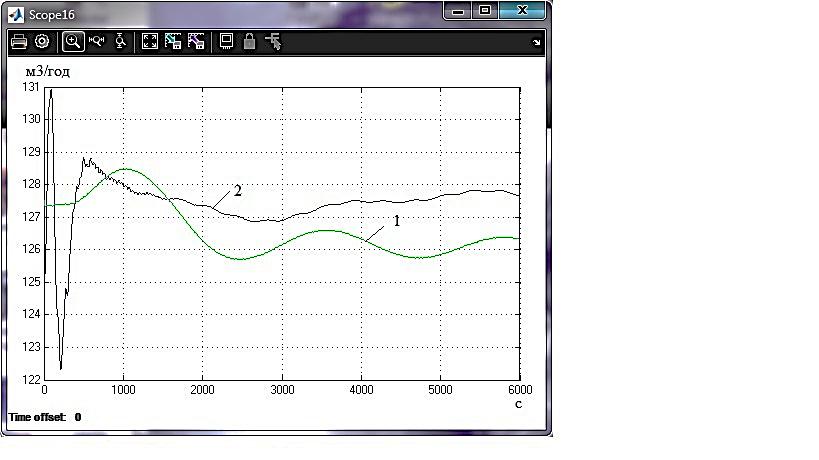
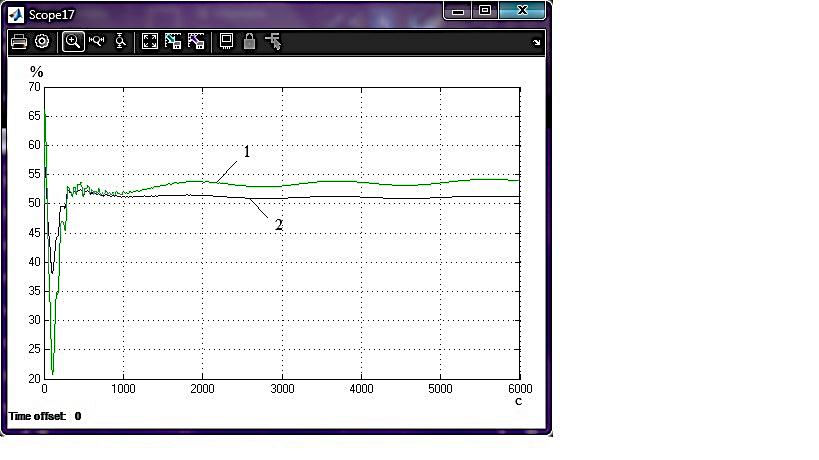 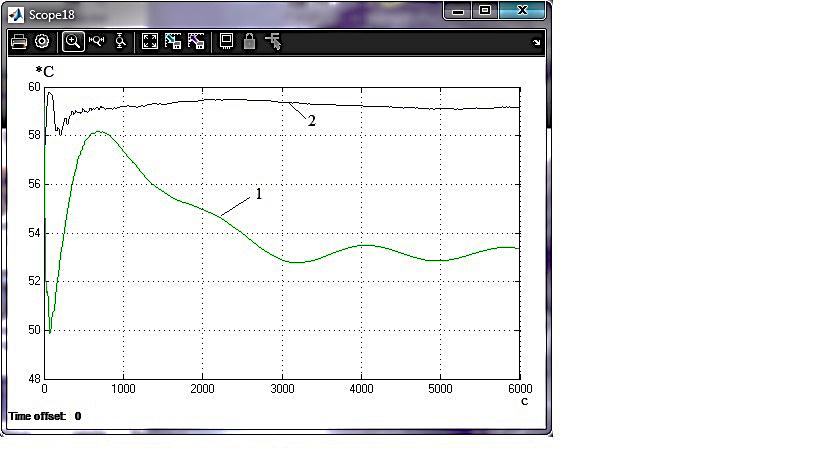 3) 4) 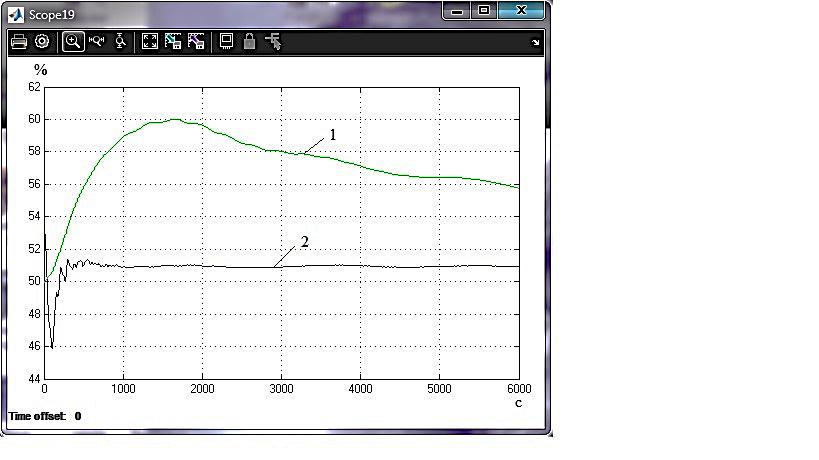 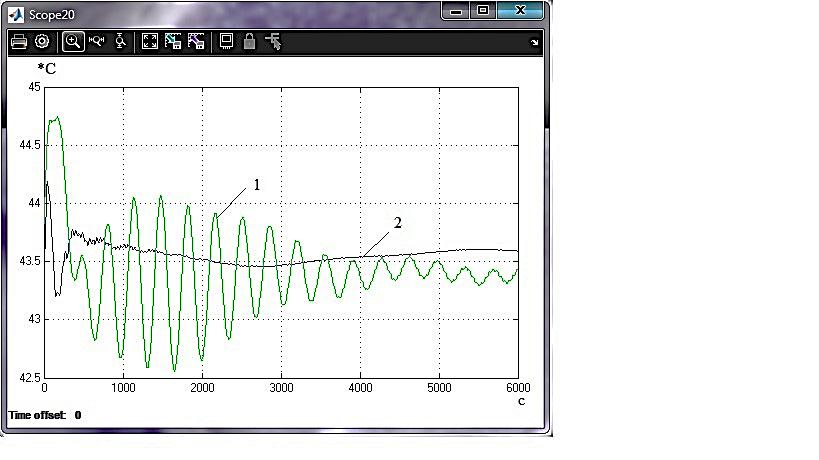 5) 6) Рисунок 4.4 – Перехідні процеси САР з лінійно-квадратичним регулятором при управлінні за збуренням -5% х.в.м. по всых каналах з використанням для синтезу регулятора стандартного (1) і модифікованого (2) критеріїв оптимальності:
Як бачимо з графіків перехідних процесів (рис.4.4), використання модифікованого критерію для синтезу лінійно-квадратичного регулятора в порівнянні зі стандартним дозволяє підвищити якість системи регулювання, що особливо актуально для складних технологічних об'єктів управління, таких як атмосферна колона ректифікації К-2. Перехідні процеси мають значно меншу статичну помилку, також зменшився час регулювання та величина перерегулювання. Таблиця 4.1 – Показники критеріїв якості регуляторів
4.3 Розробка системи автоматичного керування з використанням лінійно-квадратичного ПІ-регулятора з наглядачем стану і моделлю збурень Найбільш досконалим є регулятор, що структурно складається з трьох частин [34]:
Регулятор стану для лінійних систем (рис 4.4) має вигляд: 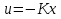 , ,де: K – матриця параметрів регулятора, що підлягає визначенню; x – вектор стану об'єкта управління, найчастіше недоступний безпосередньому виміру, оскільки вимірюється вихід об'єкта y.  Рисунок 4.4 – Регулятор стану лінійних систем Спостерігач стану є практично тією ж моделлю, що і модель керованої системи, але скориговану спеціальною матрицею спостерігача L. Структурна схема спостерігача для системи A, B, C в безперервному і дискретному часі має вигляд:  Рисунок 4.5 – Спостерігач стану Оскільки в системах управління технологічними процесами в якості стандартних прийняті стрибкоподібні збурення, а моделлю стрибка є інтегратор, то в якості моделі збурень в регулятор включається інтегратор. Структурна схема замкнутої системи управління в дискретному часі показана на рисунку 4.6. 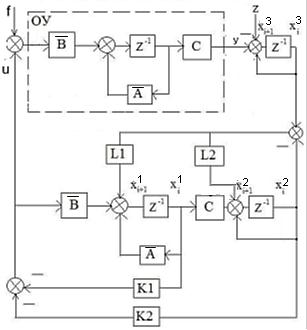 Рисунок 4.6 – Структурна схема замкнутої системи в дискретному часі А, В, С – матриці об'єкту в дискретному часі; K1 – матриця налаштування пропорційної частини регулятора стану; K2 – матриця налаштування інтегральної частини регулятора стану; L1 – матриця налаштування пропорційної частини спостерігача; L2 – матриця налаштування інтегральної частини спостерігача; z - завдання; f - збурення; u - управління. Регулятор записується у наступному вигляді: 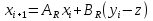 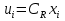 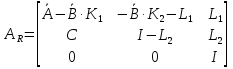 , , 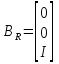 , , 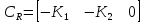 Розв´язок рівняння Ріккаті в Matlab: 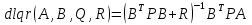 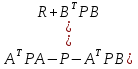 Алгоритм розрахунку регулятора: 1) Формується розширена модель системи, що включає послідовно з'єднані моделі вихідної системи і збурень; 2) Формуються початкові регулюючі матриці; 3) Вирішуються 2 рівняння Ріккаті для регулятора стану K і спостерігача L; 4) Формуються матриці регулятора AR, BR, CR; 5) Моделюється перехідний процес при подачі максимальних збурень і відхиленні завдання; 6) Якщо виходи системи відхиляються більше регламентних значень, то збільшується діагональний елемент матриці S, що відповідає номеру відхиленого виходу; 7) Якщо керуючий вплив перевищує обмеження, то збільшують діагональний елемент матриці R, що відповідає номеру управління, що перевищилось і повертаються до п.3; 8) Якщо не вдається підібрати матриці S і R, зменшують максимальну величину відхилення завдання і збурення так, щоб виконувалися вимоги.[10] Для синтезу багатомірного ПІ-регулятора за заданим алгоритмом у пакеті Matlab була розроблена програма, наведена у Додатку Д. За результатами розрахунків отримані перехідні процеси (рис. 4.7). 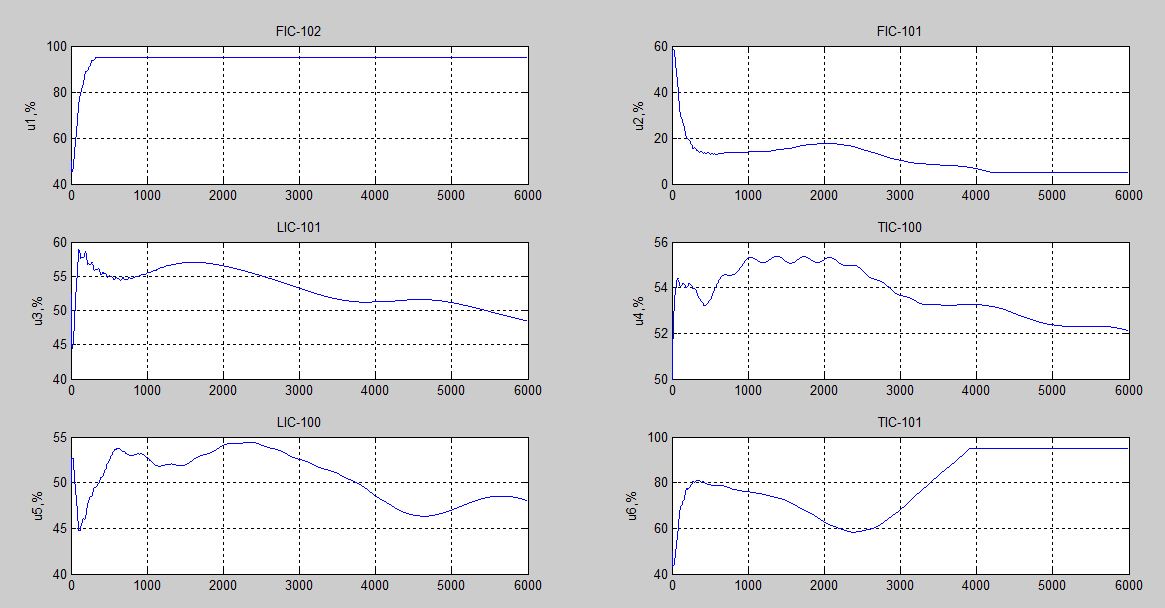 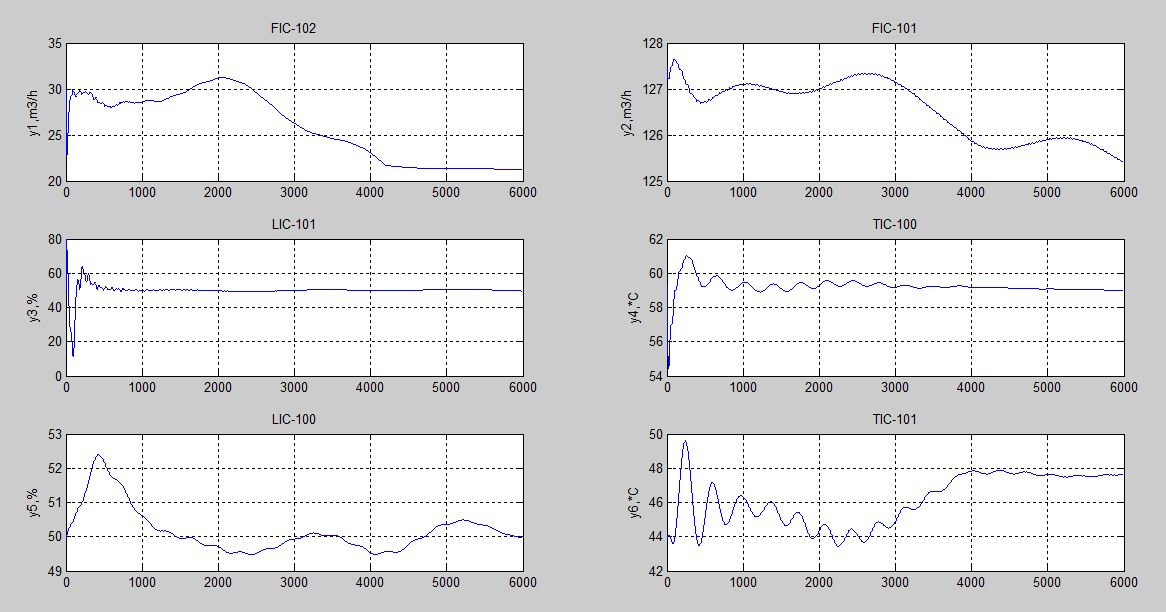 Рисунок 4.7 - Перехідні процеси ПИ регулятор дает большие отклонения (из-за слабой применимости к нему данного критерия), но зато почти нет статической ошибки. Таблиця 4.2 – Показники критеріїв якості регулятора
4.4 Розробка системи автоматичного керування з використанням MPC регулятора Одним із сучасних формалізованих підходів до аналізу і синтезу систем керування, що базуються на математичних методах оптимізації, є теорія керування динамічними об'єктами з використанням прогнозуючих моделей - Model Predictive Control (MPC). Цей підхід почав розвиватися на початку 60-х років для керування процесами та устаткуванням у нафтохімічному і енергетичному виробництві, для яких застосування традиційних методів синтезу було вкрай ускладнене у зв'язку з винятковою складністю математичних моделей. Основною перевагою MPC-підходу, що визначає його успішне використання в практиці побудови та експлуатації систем керування, служить відносна простота базової схеми формування зворотного зв'язку, що сполучається з високими адаптивними властивостями. Остання обставина дозволяє управляти багатомірними і багатозв'язними об'єктами зі складною структурою, що включає нелінійності, оптимізувати процеси в режимі реального часу в рамках обмежень на керуючі і керовані змінні, ураховувати невизначеності в завданні об'єктів і збурень. Крім того, можливий облік транспортного запізнювання, облік змін критеріїв якості в ході процесу й відмов датчиків системи виміру. Суть MPC-підходу становить наступна схема керування динамічними об'єктами за принципом зворотного зв'язку:
Загальна структурна схема управління з прогнозуванням наведена на рисунку 4.1. 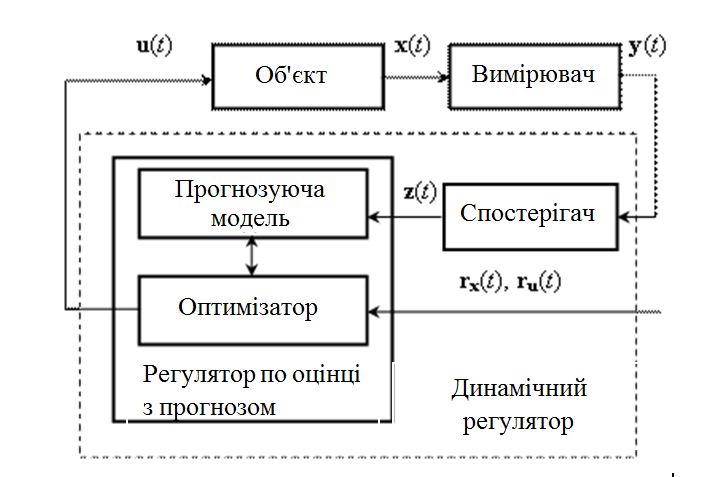 Рисунок 4.1 - Блок-схема керування із прогнозуванням Найпростішим прикладом прогнозуючої моделі можна вважати будь-який асимптотичний спостерігач, сформований для системи, яка лінеаризована в околиці свого нульового положення рівноваги при деякому номінальному поєднанні факторів невизначеності. Схему здійснення прогнозу можна проілюструвати за допомогою рис. 4.2 [7]. 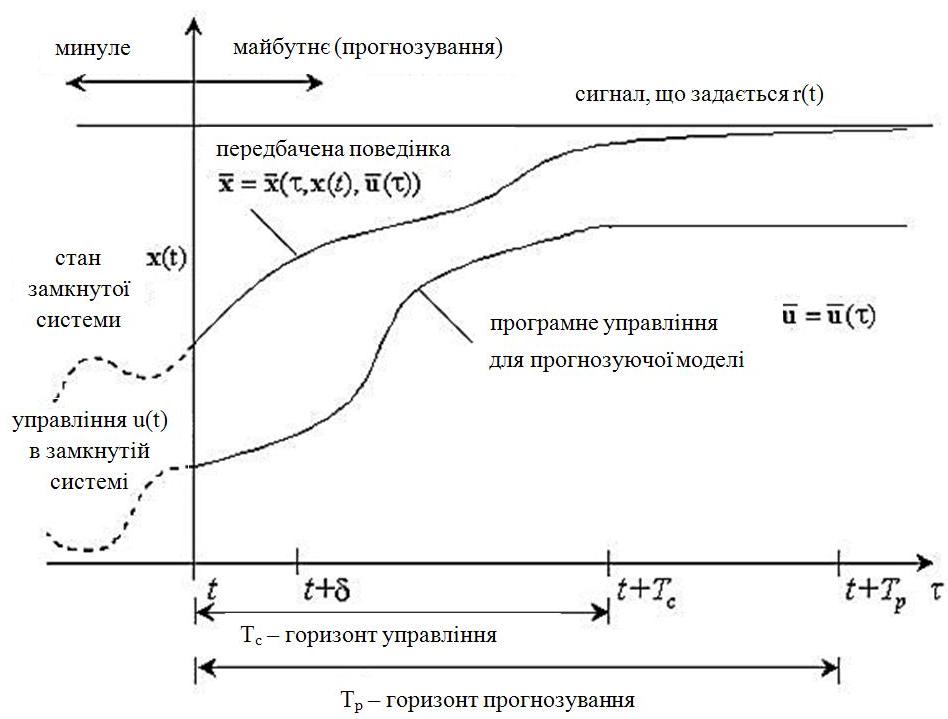 Рисунок 4.2 – Схема здійснення прогнозу Розглянемо завдання управління з лінійною моделлю і квадратичним функціоналом [2]. Нехай об'єкт управління описується лінійною системою диференційних рівнянь виду: 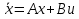 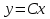 де:А – п×п матриця, u – п×т матриця, С – r×п матриця. Для оцінки якості процесу управління вводиться квадратичний функціонал: 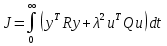 де: у и и – функції від t, R – r×r та Q – т×т — позитивно-визначені симетричні квадратні матриці; λ - постійний позитивний коефіцієнт. Визначимо кінцеву послідовність xj, i= 1, ..., р як прогноз руху об'єкта з горизонтом прогнозу р. Оптимальне управління шукається у вигляді: 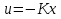 Алгоритм пошуку керуючого впливу в цьому МРС-законі представляється так. Для вихідних матриць, представлених А, В, С і горизонтом прогнозу р, формуються допоміжні матриці L і М за наступними формулами: 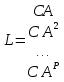 ; ; 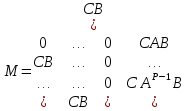 Використовуючи R і Q, обчислюється матриця K1 за формулою: 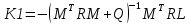 Виділяються верхні блоки розміром т×п з К1 і приймаються в якості матриці К. В системі Matlab пакету MPC Tools існує вбудована функція lqr і dlqr (для дискретного процесу), що дозволяє отримати коефіцієнт К, маючи відомі описані вище матриці А, В, R, Q. У найпростішому випадку це виглядає так: 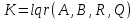 За допомогою пакета прикладних програм Model Predictive Control Toolbox (MPC Tools) в Matlab побудуємо МРС-регулятор. Для цього завантажимо одержані матриці у просторі станів до MPC Design Task. Діалог налаштувань регулятора наведено на рисунку 4.2. 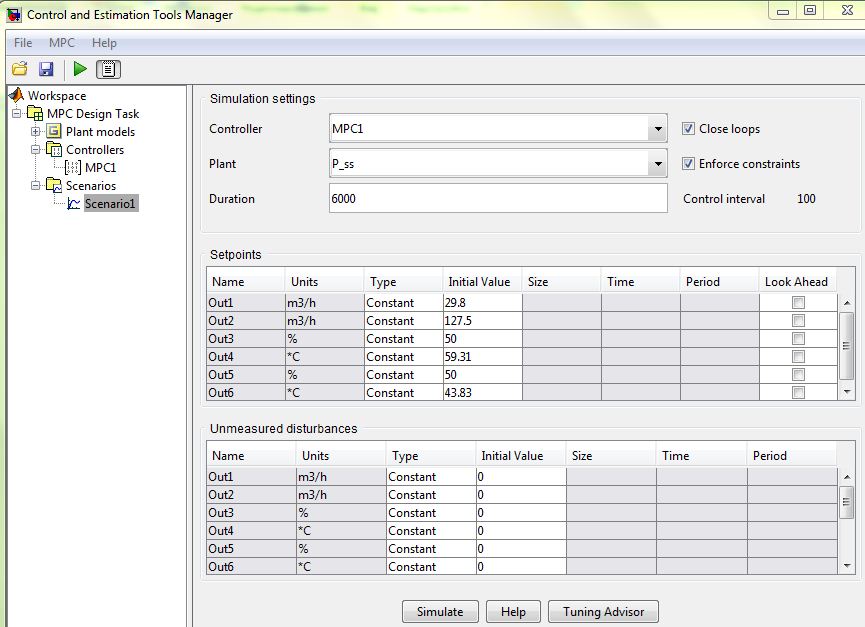 Рисунок 4.2 – Налаштування MPC Результати моделювання представлено на рис. 4.3. 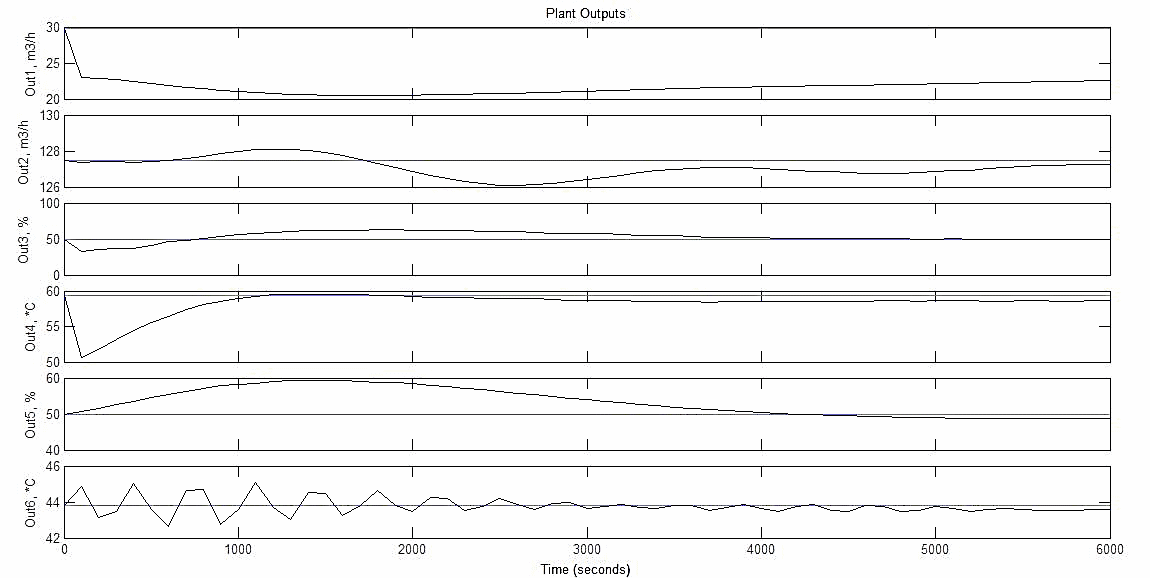 Рисунок 4.3 – Графіки перехідних процесів з використанням MPC-регулятора Таблиця 4.3 – Показники критеріїв якості регулятора
По существу, МРС-подход в линейно-квадратичной постановке без ограничений даёт один из способов формирования квазиоптимальных управлений по отношению к дискретной задаче. К достоинствам подхода здесь лишь можно отнести существенное упрощение вычислительной процедуры поиска коэффициентов по сравнению с классической дискретной оптимизацией, вклю чающей решение уравнения Риккати. Фактически это упрощение достигается за счёт отказа от априорного учёта требования устойчивости и за счёт конечности интервала, на котором рассмат ривается процесс. При этом процедура настройки регулятора может быть реализована в режиме реального времени непосредственно перед его функциональным использованием, например, на борту подвижного объекта. Однако ситуация принципиально меняется при учёте ограничений на управления и контролируемые переменные, существенно сужающих допустимое множество регуляторов в задаче LQR-оптимизации. Здесь построение точного оптимального решения в реальном времени весьма проблематично, что зна чительно повышает обоснованность привлечения МРС-подхода. МРС-подход с учётом ограничений на управляющие воздействия позволяет существенно повысить качество переходных процессов: уменьшить время и снизить перерегулирование по выходным коор динатам по сравнению с LQR -о пт и мал ь н ы м синтезом. Решение оптимальных задач управления с прогнозированием является одним из современных ме тодов исследования систем управления и легко реализуется с помощью таких систем как МАТLАВ, которая с её пакетами обладает большими возможностями и инструментами решения задач анализа, синтеза и моделирования систем управления, в том числе и с прогнозированием. Это позволяет прив лекать её для решения реальных примеров по управлению всевозможными технологическими процес сами и внедрения новинок в производстве, например, по управлению нестационарными режимами технологических процессов. |