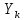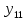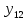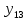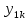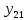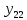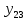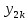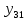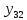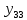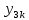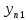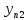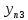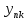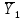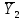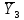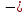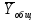ВКР Шаркова bb17-01. Владивостокский государственный университет экономики и сервиса институт цифровой экономики и бизнесаналитики
 Скачать 5.28 Mb. Скачать 5.28 Mb.
|
1.2 Обзор методов анализа статистических данных1.2.1 Непараметрический критерий анализа зависимости Хи-квадрат Проверка статистических гипотез является типовой задачей многомерного статистического анализа. Для проверки статистических гипотез используются статистические критерии [13]. Статистический критерий – строгое математическое правило, по которому принимается или отвергается та или иная статистическая гипотеза. Построение критерия представляет собой выбор подходящей функции от результатов наблюдений (ряда эмпирически полученных значений признака), которая служит для выявления меры расхождения между эмпирическими значениями и гипотетическими. Выбор статистического критерия, отвечающего практической задаче, может быть осуществлен согласно таблице 1. Методика применения статистических критериев для зависимых и независимых выборок отличаются. Независимые выборки: сравниваются две разные группы, например, мужчины и женщины, молодые и пожилые и т.д. Зависимые выборки, как правило, возникают тогда, когда речь идет об одной группе испытуемых до и после экспериментального воздействия. Так же зависимыми выборками могут быть, например, мужья и жены, близнецы и т.п. При этом предполагается, что в данных они (семья, пара близнецов, испытуемый до или после эксперимента) занимают одну, а не две строчки. Соответственно, зависимые выборки всегда имеют одинаковый объем, а объем независимых может отличаться [14]. Таблица 1 – Условия применения статистических критериев
Таблица сопряженности является наиболее универсальным средством изучения статистических связей. В ней могут быть представлены переменные, измеренные в любой шкале. Основным критерием для проверки гипотезы о наличии связи между признаками на основе таблицы сопряженности является критерий 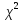 -квадрат Пирсона. -квадрат Пирсона. Для оценки достоверности различий по методу хи-квадрата Пирсона (критерий соответствия, коэффициент согласия) анализируются различия между реальными существующими частотами в группах (Observed) и рассчитываемыми по формуле ожидаемыми «гипотетическими» частотами, которые соответствуют распределению хи-квадрат. При малом различии ожидаемых и наблюдаемых частот (хи-квадрат не достиг своего критического значения) мы принимаем нулевую гипотезу об отсутствии различий. Если же различия оказываются существенными (критическое значение хи-квадрата достигается для заданного числа степеней свободы) нулевая гипотеза отвергается и говорят о наличии статистически значимых различий. Принцип работы критерия демонстрируется на рисунке 5. Пусть таблица сопряженности двух признаков X и Y, содержит, соответственно, q и m категорий. С помощью критерия хи-квадрата Пирсона проверяется статистическая гипотеза: 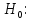 связь между признаками X и Y отсутствует. связь между признаками X и Y отсутствует.При конкурирующей гипотезе: 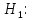 связь между признаками X и Y статистически значима. связь между признаками X и Y статистически значима.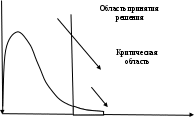 Рисунок 5 – Функция плотности распределения 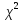 Основная формула для расчета хи-квадрата Пирсона: 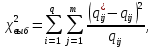 где 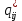 – выборочные частоты из таблицы сопряженности; – выборочные частоты из таблицы сопряженности; – теоретические частоты, рассчитанные по таблице сопряженности, исходя из – теоретические частоты, рассчитанные по таблице сопряженности, исходя из предположения отсутствия связи между признаками X и Y. Гипотеза 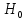 принимается при уровне значимости принимается при уровне значимости 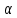 , если , если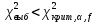 В этом случае количество степеней свободы (Degree of freedom – d.f.) определяется по формуле; 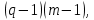 где q – количество строк таблицы сопряженности; m – количество столбцов таблицы сопряженности. 1.2.2 Непараметрический критерий ранговой корреляции СпирменаКоэффициент ранговой корреляции Спирмена применяется для измерения тесноты статистической связи между двумя ранжированными признаками. Ранговая корреляция – это метод корреляционного анализа, отражающий отношения переменных, упорядоченных по возрастанию их значения. Коэффициент корреляции рангов, предложенный К. Спирменом, относится к непараметрическим показателям связи между переменными, измеренными в ранговой шкале. При расчете этого коэффициента не требуется никаких предположений о характере распределений признаков в генеральной совокупности. Этот коэффициент определяет степень тесноты связи порядковых признаков, которые в этом случае представляют собой ранги сравниваемых величин. Коэффициент ранговой корреляции Спирмена – это некоторое число от минус 1 до 1, характеризующее силу линейной связи между рангами двух случайных величин. Для решения задач ранговой корреляции исходные данные представляются в виде таблиц «объект-свойство», состоящей из элементов 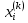 , , 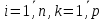 , определяющих ранг i-того объекта по k-тому свойству. , определяющих ранг i-того объекта по k-тому свойству.Величины 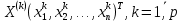 , образующие столбцы матрицы «объект-свойство», называются ранжировками. Под ранговой корреляцией понимается изучение статистической связи между ранжировками , образующие столбцы матрицы «объект-свойство», называются ранжировками. Под ранговой корреляцией понимается изучение статистической связи между ранжировками 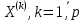 . .Коэффициент корреляции Спирмена измерения тесноты статистической связи между двумя ранжировками 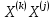 определятся по формуле: определятся по формуле: 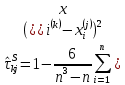 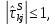 причем причем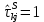 , если , если 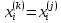 , , 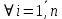 , то есть ранги совпадают, , то есть ранги совпадают,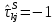 , если , если 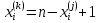 , , 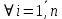 , то есть ранги противоположны. , то есть ранги противоположны.Если хотя бы в одной из ранжировок имеются повторяющиеся ранги, вычисляют поправку: 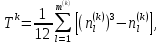 где 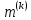 – число групп повторяющихся рангов; – число групп повторяющихся рангов;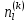 – число совпадающих рангов в l-той группе. – число совпадающих рангов в l-той группе.С учетом поправок коэффициент корреляции Спирмена вычисляется по формуле: 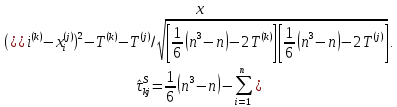 Для вычисления коэффициента Спирмена в EXCEL удобно ввести обозначение некоторых элементов общей формулы: 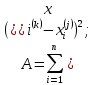 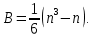 С учетом обозначений формула коэффициента Спирмена будет иметь вид: 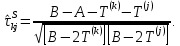 Для проверки статистической значимости коэффициента Спирмена используется распределение Стьюдента. Проверяется нулевая гипотеза: 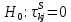 в равенстве генерального коэффициента ранговой корреляции. в равенстве генерального коэффициента ранговой корреляции.При конкурирующей гипотезе 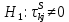 . .Гипотеза 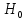 принимается при уровне значимости принимается при уровне значимости 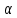 , если , если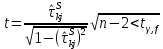 , ,где 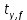 – пороговое значение распределения Стьюдента с параметрами – пороговое значение распределения Стьюдента с параметрами 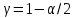 , , 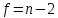 . .1.2.3 Дисперсионный анализВ дисперсионном анализе проверяется гипотеза, которая является обобщением гипотезы равенства двух средних на случай, когда проверяется гипотеза равенства одновременно нескольких средних. В дисперсионном анализе исследуется степень влияния одного или нескольких факторных признаков на результативный признак. Идея дисперсионного анализа принадлежит Р. Фишеру. Он использовал его для обработки результатов агрономических опытов. Дисперсионный анализ применяется для установления существенности влияния качественных факторов на исследуемую величину. Английское сокращенное название дисперсионного анализа – ANOVA (analysis variation). Общая форма представления данных с классификацией по одному признаку представлена в таблице 2. Каждый набор значений по столбцам соответствует набору значений одного и того же признака, соответствующего определенному правилу классификации. То есть такая таблица может быть получена по таблице данных, содержащей два столбца. В первом столбце исходной таблицы располагаются значения исследуемого признака, во втором – номера классов заданной классификации. На практике количество наблюдений по столбцам совпадает далеко не всегда. Поэтому при рассмотрении расчетных формул мы будем рассматривать более общий случай, считая, что количество значений в столбцах различно и равно 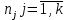 , где k – количество классов в классификации. , где k – количество классов в классификации.Средние по столбцам рассчитаем по формуле: 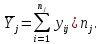 Таблица 2 – Форма представления данных с классификацией по одному признаку
Тогда, учитывая, что общее число наблюдений во всех столбцах равно 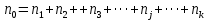 , общее среднее рассчитаем по формуле: , общее среднее рассчитаем по формуле: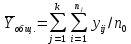 Для любого наблюдения имеет место следующее равенство: 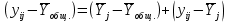 Соотношение показывает, что отклонение наблюдения от общего среднего может быть разделено на две части. Первая часть — это отклонение среднего по столбцу от общего среднего (отклонение по столбцу) или факторное отклонение. Вторая часть – это отклонение наблюдения от среднего по столбцу (остаточное отклонение). Возведем отклонения в формуле в квадрат и просуммируем значения по всем наблюдениям. Тогда получим меры вариации: 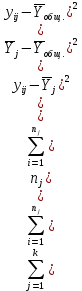 В словесной формулировке эту формулу можно записать следующим: Общая вариация = Вариация столбцов + Остаточная вариация. Это соотношение называется основным тождеством вариации: оно разделяет общую вариацию наблюдений на вариацию, обусловленную классификацией столбца, и вариацию, обусловленную случайной ошибкой. Обозначим общую вариацию 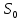 : :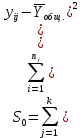 Вариацию столбцов обозначим 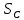 : :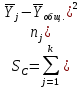 Остаточная вариация может быть рассчитана, как по общей формуле, так и как разность общей вариации и вариации столбцов: 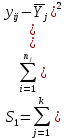 Статистическая гипотеза состоит в том, что все средние по столбцам равны некоторому общему среднему. Если гипотеза справедлива, то вариация столбцов 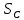 будет достаточно мала по сравнению с остаточной вариацией будет достаточно мала по сравнению с остаточной вариацией 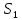 . Гипотеза проверяется с помощью критерия Фишера: . Гипотеза проверяется с помощью критерия Фишера: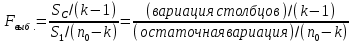 В формуле 18 вариация делится на количество степеней свободы (использованных связей). Так как 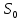 и и 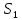 имеют соответственно имеют соответственно 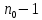 и и 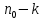 степеней свободы, то степеней свободы, то 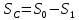 имеет имеет 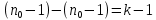 степеней свободы. степеней свободы.По таблице распределения Фишера при уровне значимости 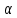 и степенях свободы и степенях свободы 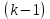 и и 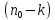 определяем критическое значения критерия Фишера. определяем критическое значения критерия Фишера.1.2.4 Метод многомерной классификации k-среднихМетодом k - средних был предложен Мак-Куином. Этот метод классификации относится к группе итеративных методов классификации. Для начала процедуры классификации должны быть заданы k выбранных объектов, которые будут служить эталонами, т.е. центрами кластеров. Метод k-средних удобен для обработки больших статистических совокупностей. Рассмотрим алгоритм метода k-средних. Пусть имеется n объектов (наблюдений), каждый из которых характеризуется m признаками 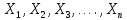 . Необходимо разбить наблюдения на заданное число классов – (k). Для начала из n точек исследуемой совокупности отбираются случайным образом или задаются исследователем исходя из каких-либо априорных соображений k точек (объектов). Эти точки принимаются за эталоны. Каждому эталону присваивается порядковый номер, который одновременно является и номером кластера. На первом шаге из оставшихся (n – k) объектов извлекается точка . Необходимо разбить наблюдения на заданное число классов – (k). Для начала из n точек исследуемой совокупности отбираются случайным образом или задаются исследователем исходя из каких-либо априорных соображений k точек (объектов). Эти точки принимаются за эталоны. Каждому эталону присваивается порядковый номер, который одновременно является и номером кластера. На первом шаге из оставшихся (n – k) объектов извлекается точка 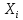 с координатами с координатами 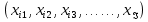 и проверяется, к какому из эталонов (центров) она находится ближе всего. Для этого используется одна из метрик, например, евклидово расстояние. Проверяемый объект присоединяется к тому центру (эталону), которому соответствует минимальное из расстояний. Эталон заменяется новым, пересчитанным с учетом присоединенной точки, и вес его (количество объектов, входящих в данный кластер) увеличивается на единицу. Если встречаются два или более минимальных расстояния, то i-ый объект присоединяют к центру с наименьшим порядковым номером. На следующем шаге выбираем точку и проверяется, к какому из эталонов (центров) она находится ближе всего. Для этого используется одна из метрик, например, евклидово расстояние. Проверяемый объект присоединяется к тому центру (эталону), которому соответствует минимальное из расстояний. Эталон заменяется новым, пересчитанным с учетом присоединенной точки, и вес его (количество объектов, входящих в данный кластер) увеличивается на единицу. Если встречаются два или более минимальных расстояния, то i-ый объект присоединяют к центру с наименьшим порядковым номером. На следующем шаге выбираем точку 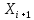 и для нее повторяются все процедуры. Таким образом, через (n - k) шагов все точки (объекты) совокупности окажутся отнесенными к одному из k кластеров, но на этом процесс разбиения не заканчивается. Для того чтобы добиться устойчивости разбиения по тому же правилу, все точки и для нее повторяются все процедуры. Таким образом, через (n - k) шагов все точки (объекты) совокупности окажутся отнесенными к одному из k кластеров, но на этом процесс разбиения не заканчивается. Для того чтобы добиться устойчивости разбиения по тому же правилу, все точки 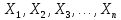 опять подсоединяются к полученным кластерам, при этом веса продолжают накапливаться. Новое разбиение сравнивается с предыдущим. Если они совпадают, то работа алгоритма завершается. В противном случае цикл повторяется. Окончательное разбиение имеет центры тяжести, которые не совпадают с эталонами, их можно обозначить опять подсоединяются к полученным кластерам, при этом веса продолжают накапливаться. Новое разбиение сравнивается с предыдущим. Если они совпадают, то работа алгоритма завершается. В противном случае цикл повторяется. Окончательное разбиение имеет центры тяжести, которые не совпадают с эталонами, их можно обозначить 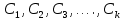 . При этом каждая точка . При этом каждая точка 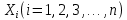 будет относиться к такому кластеру l, для которого расстояние минимально. Возможны две модификации метода k-средних. Этот метод минимизирует дисперсию внутри каждого кластера, хотя в явном виде такой критерий оптимизации не используется. будет относиться к такому кластеру l, для которого расстояние минимально. Возможны две модификации метода k-средних. Этот метод минимизирует дисперсию внутри каждого кластера, хотя в явном виде такой критерий оптимизации не используется.1.3 Возможности обработки многомерных статистических данных с помощью пакета Statistica Statistica (торговая марка – STATISTICA) – пакет для всестороннего статистического анализа, разработанный компанией StatSoft. В пакете STATISTICA реализованы процедуры для анализа данных (data analysis), управления данными (data management), добычи данных (data mining), визуализации данных (data visualization). Универсальная интегрированная система, предназначенная для статистического анализа, визуализации данных и разработки пользовательских приложений Statistica – это современный пакет, в котором реализованы все новейшие компьютерные и математические методы статистического анализа данных. Программа является наиболее динамично развивающимся статистическим пакетом и мировым лидером на рынке статистического программного обеспечения [15]. Для того чтобы собранные данные грамотно обработать и извлечь из них максимум информации, требуются немалые усилия. Программа Statistica – это надежный помощник и консультант. Она снабжена подсказками, какие методы анализа существуют и какие из них лучше всего подходят для тех или иных задач. Система избавляет пользователя от рутинных вычислений, наглядно отображает результаты анализа, помогает оптимально спланировать будущие эксперименты и создает высококачественные отчеты, оставляя специалисту удовольствие интерпретации результатов и формулировки выводов. Помимо общих статистических и графических средств, в системе имеются специализированные модули, например, для проведения социологических исследований, решения промышленных и других задач, при решении которых возникает проблема анализа статистических данных. Система обладает следующими общепризнанными достоинствами [16]: – содержит полный набор классических и продвинутых методов анализа данных; – легка в освоении подготовленным пользователем; – полностью совместима с приложениями операционной системы Windows; – является средством построения приложений в конкретных областях; – данные системы Statistica легко конвертировать в различные базы данных и электронные таблицы; – в комплект поставки входят специально подобранные примеры, позволяющие систематически осваивать методы анализа; – поддерживает большинство Интернет-форматов; – поддерживает высококачественную графику, позволяющую эффектно визуализировать данные и проводить графический анализ; – содержит язык программирования, который позволяет расширять систему и запускать ее из других Windows-приложений. Statistica работает с четырьмя различными типами документов: а) электронная таблица Spreadsheet, предназначенная для ввода исходных данных и их преобразования; б) электронная таблица Scrollsheet для вывода численных и текстовых результатов анализа; в) график− документ в специальном графическом формате для визуализации и графического представления численной информации; д) отчет− документ в формате RTF (расширенный текстовый формат) для вывода текстовой и графической информации. Одним из возможных и самых простых способов взаимодействия с системой является интерактивный режим работы, когда взаимодействие с системой осуществляется при помощи последовательного выбора различных команд из меню. Пакет Statistica обладает удобным интерфейсом, ориентированным на решение задач многомерного статистического анализа данных. Интерфейс Statistica является интуитивно понятным, легко настраивается в соответствии с пользовательскими задачами и аналогичен интерфейсу стандартных Windows-приложений, поэтому легко осваивается пользователем. Анализ данных проводится интерактивно, в режиме последовательно открывающихся диалоговых окон. Любое окно анализа сконструировано таким образом, что на первой вкладке содержатся только самые необходимые кнопки, а на последующих вкладках – углубленные методы и специальные опции. На рисунке 6 представлено главное меню, которое появляется при запуске пакета. 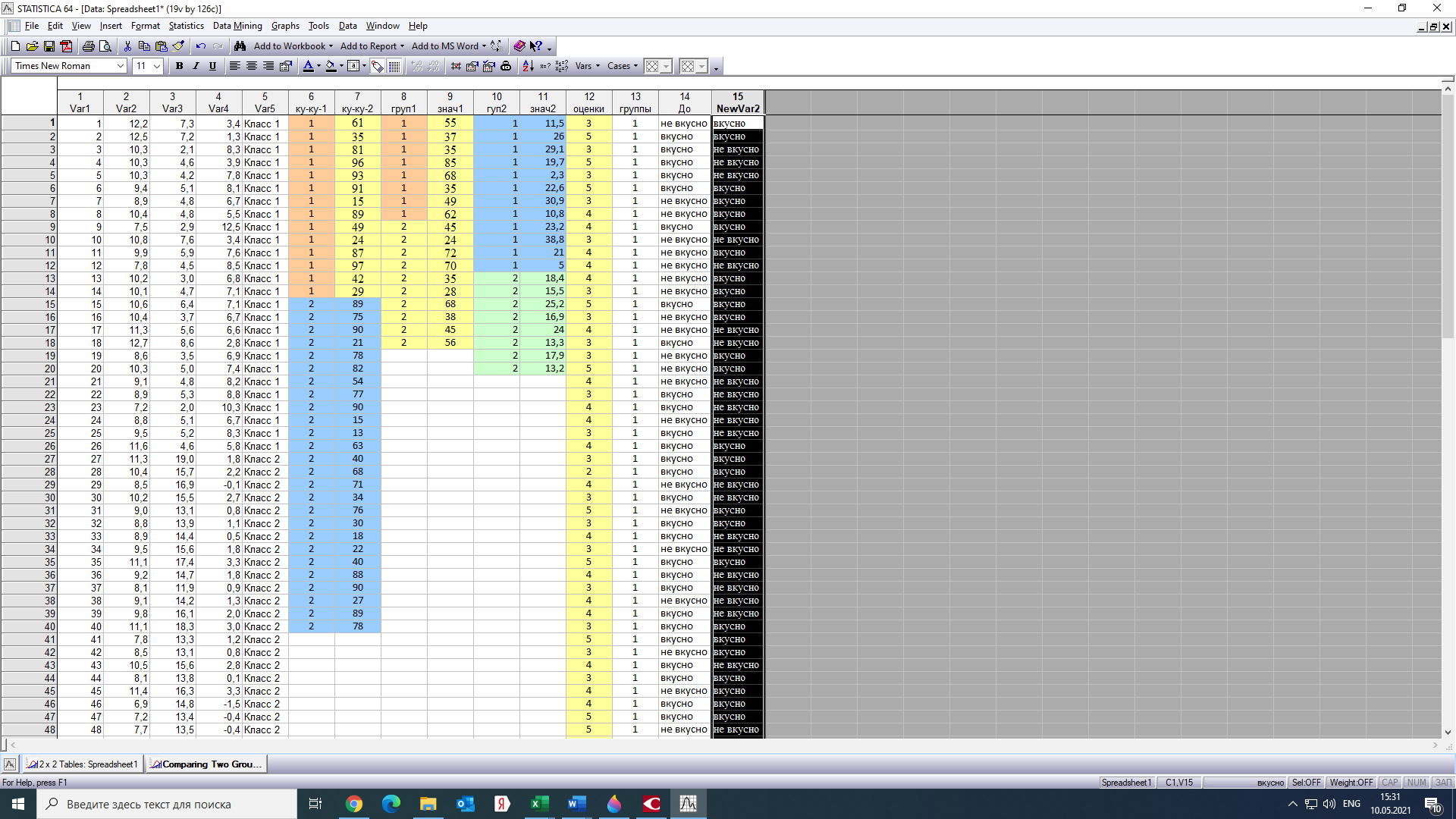 Рисунок 6 – Главное меню пакета Statistica Панель состоит из следующих опций: – файл (file); – редактирование (edit); – просмотр (veiw); – вставка (insert); – формат (format); – статистика (statistics); – графики (graphs); – инструменты (tools); – данные (data); – окно (Windows); – справка (help). Предварительный анализ данных и расчет описательных статистик применяется на первом этапе анализа данных. Инструменты, используемые на предварительном этапе анализа данных представлены в меню на рисунке 7. 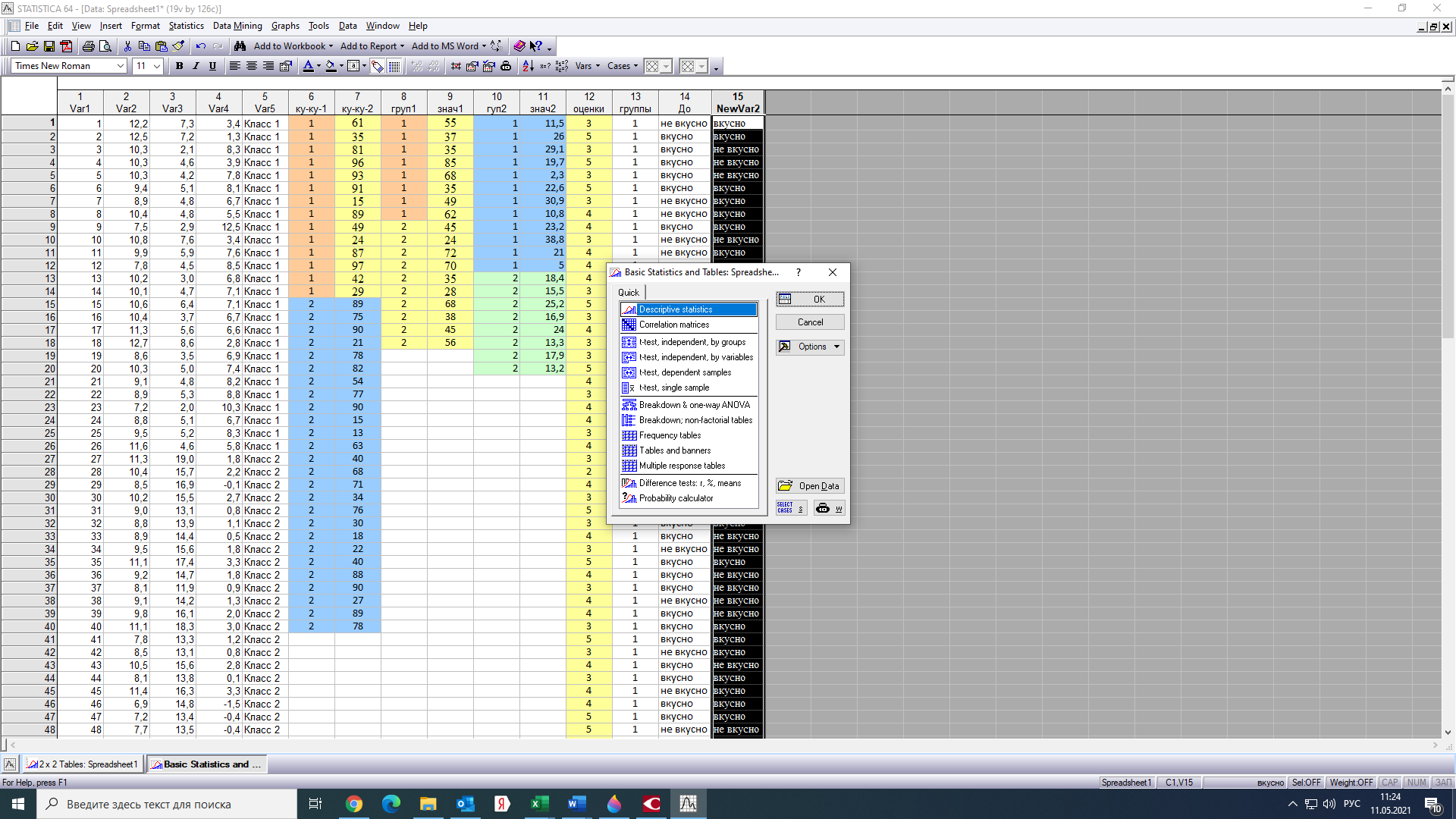 Рисунок 7 – Модули – Основные таблицы Статистические критерии могут использоваться для зависимых и независимых данных. Для обозначения различных типов данных используются пиктограммы, представленные на рисунке 8. Рисунок 8 – Пиктограммы Выбор статистических методов анализа данных производится с помощью пункта меню Statistics. На рисунке 9 представлено меню выбора метода многомерного анализа данных. 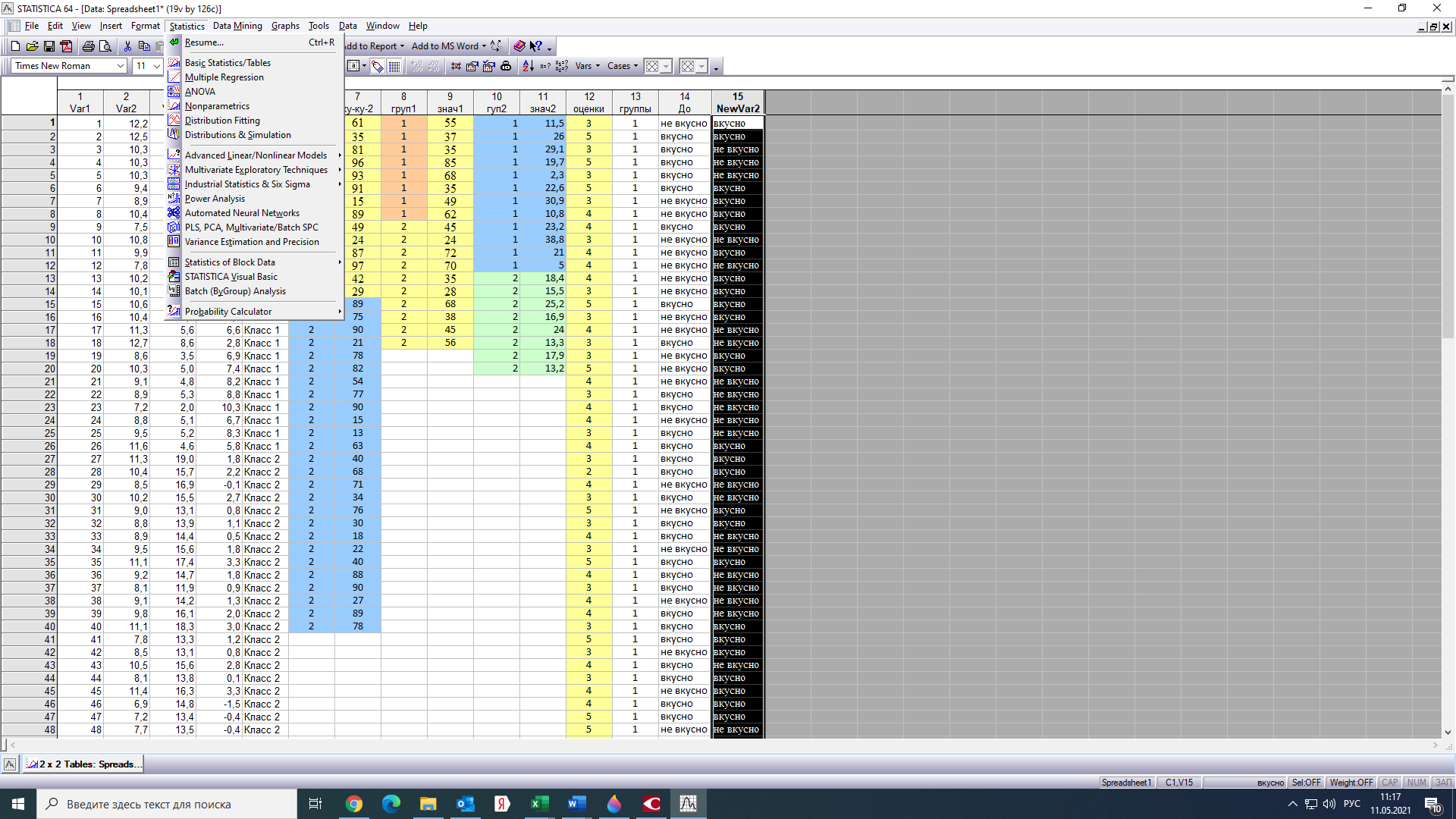 Рисунок 9 – Меню выбора Для обработки ранговых и порядковых данных используются непараметрические критерии. В пакете Statistica представлен широкий спектр непараметрических критериев, которые, называются в программе статистике, как модули проверки статистических гипотез с помощью непараметрических критерии, они представлены на рисунке 10 [17]. При проверке статистических гипотез задаются определенным уровнем значимости. Критические значения наиболее распространенных статистически функций, используемых в статистических критериях, можно вычислить с помощью вероятностного калькулятора (рисунок 11). Команда Probability Distribution Calculator открывает «Калькулятор вероятностных распределений» с интерактивными графиками функций распределения и плотностей, которые автоматически обновляются при изменении параметров. 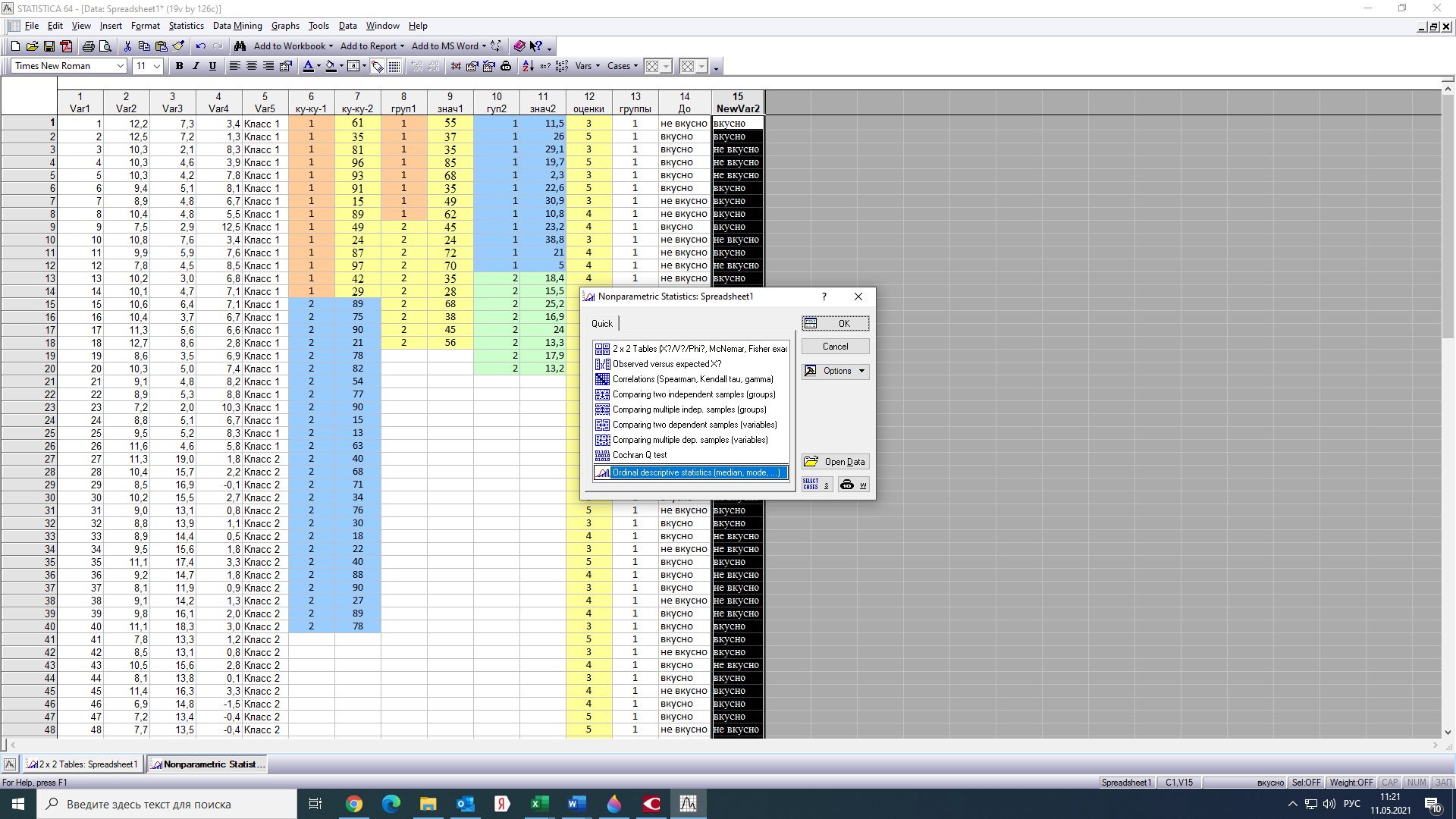 Рисунок 10 – Модули проверки Этот достаточно гибкий инструмент можно использовать для исследования форм множества теоретических распределений. Кроме того, он предоставляет процедуры для вычисления вероятностей для различных тестовых статистик, а также критических значений. Например, критическое значение для распределения хи-квадрат, при уровне значимости p=0,05 для числа степеней свободы df=9 представлено на рисунке 11. 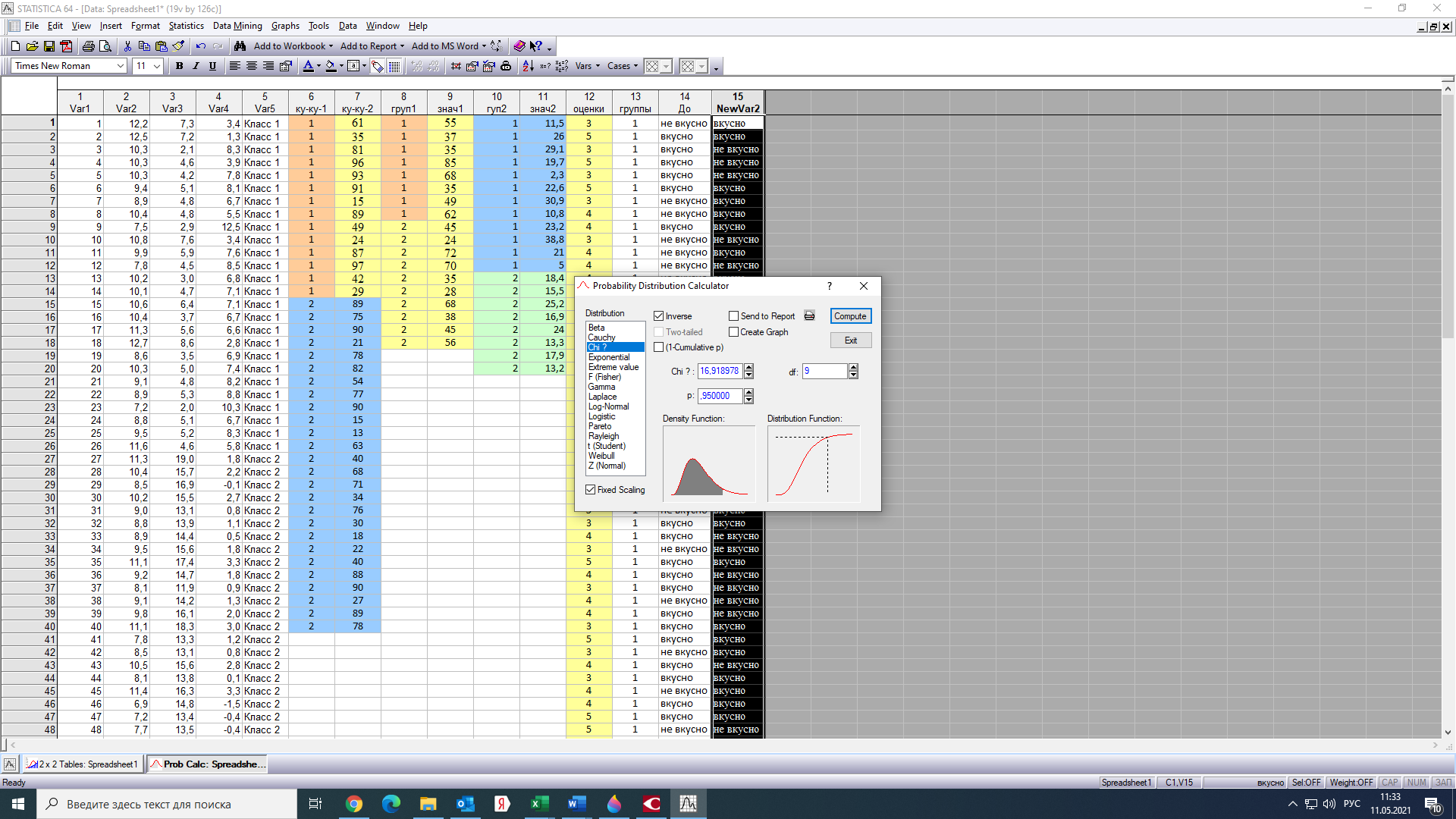 Рисунок 11 – Вероятностный калькулятор В реальных статистических исследованиях учитывается неоднородность данных. Для выделения однородных групп используются различные методы группировки. Группировкой называется разбиение общей совокупности единиц объекта наблюдения по одному или нескольким существенным признакам на однородные группы, различающиеся между собой в количественном и качественном отношениях и позволяющие выделить социально-экономические типы, изучить структуру совокупности и проанализировать связи между отдельными признаками. Группировки являются важнейшим статистическим методом обобщения статистических данных, основой для правильного исчисления статистических показателей. С помощью метода группировок решаются следующие задачи: – выделение социально-экономических типов явлений; – изучение структуры явления и структурных сдвигов, происходящих в нем; – выявление взаимосвязи и взаимозависимости между явлениями. В соответствии с поставленными задачами, решаемыми в ходе построения статистических группировок, различают следующие их виды: типологические, структурные, аналитические. Пакет Statistica включает обширный перечень графического анализа сгруппированных данных. Меню выбора графических методов анализа сгруппированных данных представлено на рисунке 12. Типологическая группировка – это разбиение разнородной совокупности единиц наблюдения на отдельные качественно однородные группы и выявление на этой основе социально-экономических типов явлений. При построении группировки такого вида главное внимание должно быть уделено идентификации типов и выбору группировачного признака. Решение вопроса об основании группировки должно осуществляться на базе анализа сущности изучаемого социально-экономического явления [18]. Структурная группировка предназначена для изучения состава однородной совокупности по какому-либо варьирующему признаку, а также структуры и структурных сдвигов, происходящих в нем. 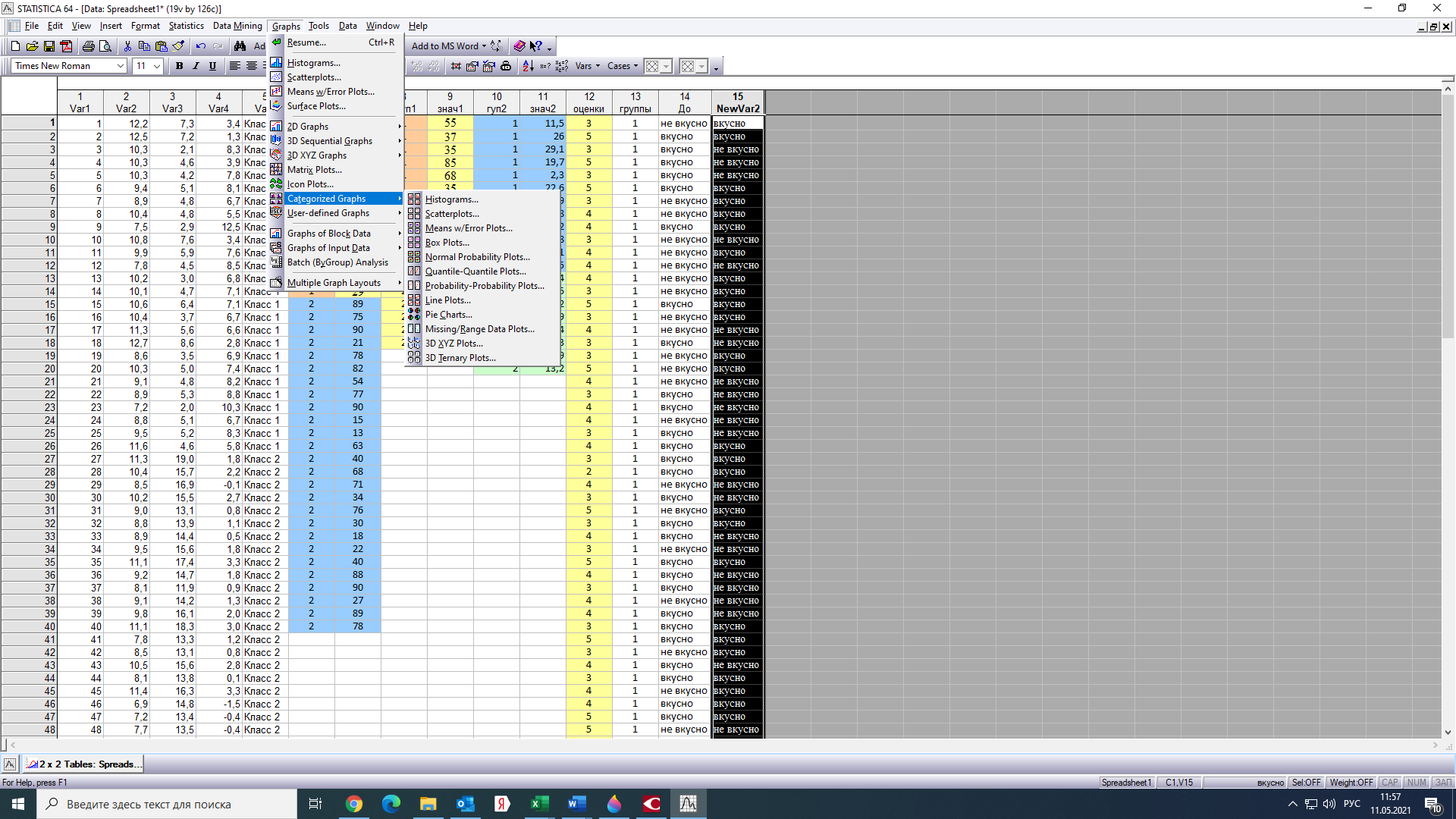 Рисунок 12 – Меню выбора методов Группировка, выявляющая взаимосвязи между изучаемыми явлениями и признаками, их характеризующими, называется аналитической группировкой. Существует несколько методов выделения категорий: – по целым значениям группирующих переменных (целые числа); – разделением группирующих переменных на заданное число интервалов (категории); – разделением группирующих переменных на интервалы с заданными граничными значениями (границы); – с помощью задания конкретных значений (кодов) группирующих переменных; – путем формирования сложных подгрупп (сложные подгруппы). Многомерная классификация может быть произведена с помощью одного из алгоритмов кластеризации. Наиболее распространенным алгоритмом кластеризации является алгоритм k-средних (рисунок 13). 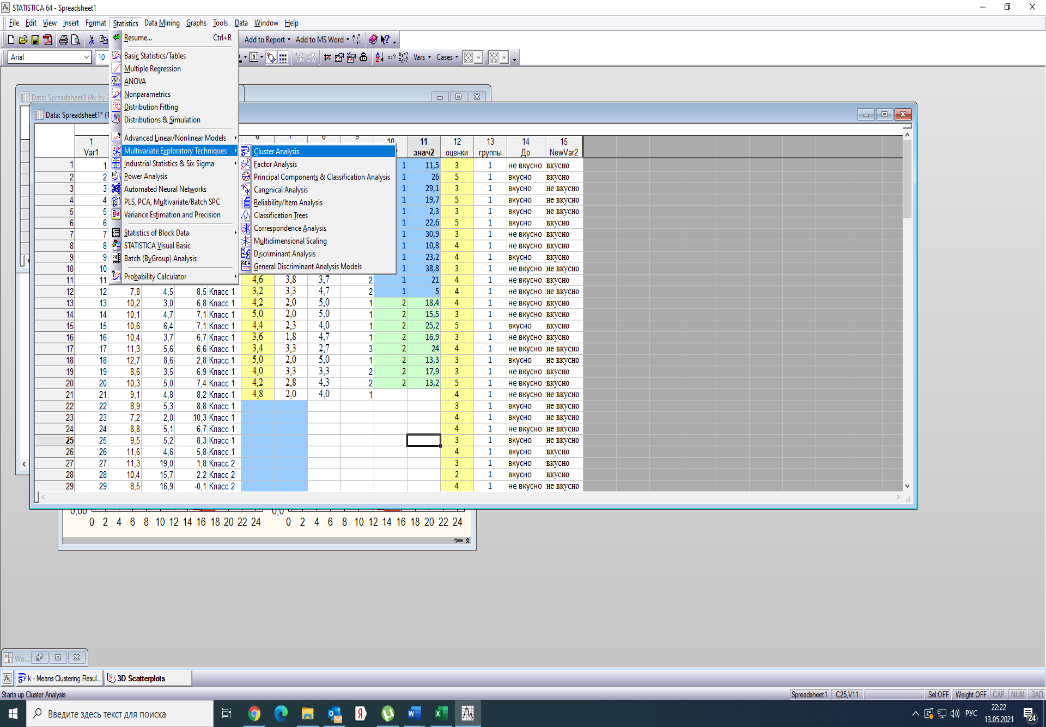 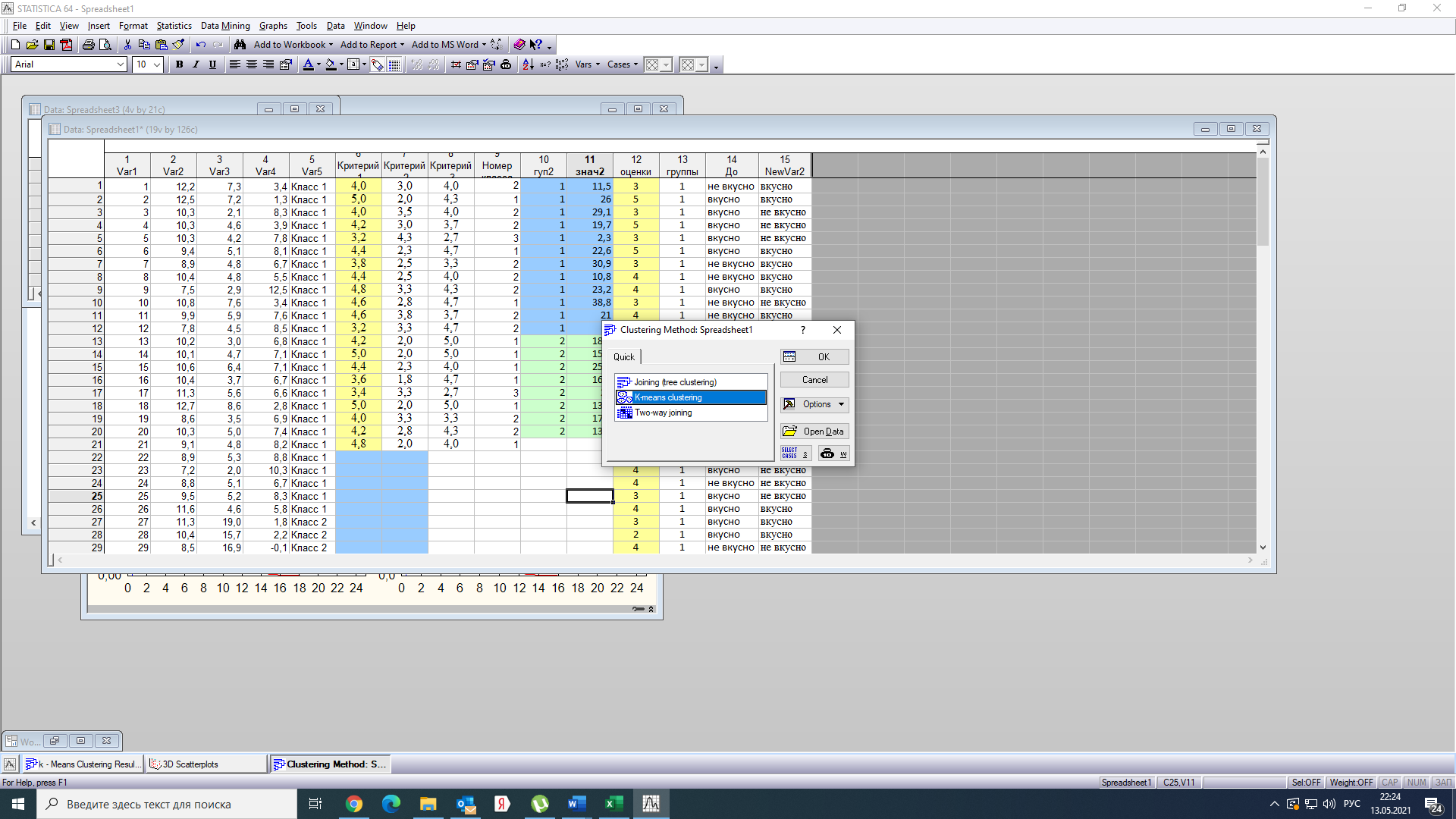 Рисунок 13 – Меню выбора алгоритма классификации В результате работы алгоритма каждому наблюдению устанавливается номер класса. Программа классификации рассчитывает различные параметры классов по выбору исследователя. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

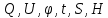
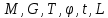
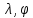
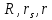
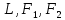
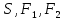
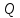 – критерий Розенбаума;
– критерий Розенбаума;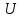 – критерий Манна-Уитни;
– критерий Манна-Уитни;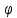 – критерий (угловое преобразование) Фишера;
– критерий (угловое преобразование) Фишера;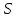 – критерий тенденций Джонкира;
– критерий тенденций Джонкира;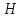 – критерий Крускала-Уоллиса;
– критерий Крускала-Уоллиса;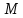 – критерий Макнамары;
– критерий Макнамары;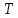 –
– 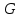 – критерий знаков;
– критерий знаков;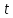 – критерий Стьюдента;
– критерий Стьюдента;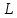 – критерий тенденций Пейджа;
– критерий тенденций Пейджа;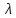 – критерий Колмогорова-Смирнова;
– критерий Колмогорова-Смирнова;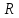 – обобщенное обозначение критериев корреляционного анализа (ассоциации Юла, контингенции Пирсона, взаимной сопряженности Пирсона и Чупрова);
– обобщенное обозначение критериев корреляционного анализа (ассоциации Юла, контингенции Пирсона, взаимной сопряженности Пирсона и Чупрова);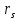 – критерий ранговой корреляции Спирмена;
– критерий ранговой корреляции Спирмена;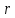 – критерий линейной корреляции Пирсона;
– критерий линейной корреляции Пирсона;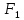 – критерий Фишера для однофакторного дисперсионного анализа;
– критерий Фишера для однофакторного дисперсионного анализа;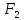 – критерий Фишера для двухфакторного дисперсионного анализа
– критерий Фишера для двухфакторного дисперсионного анализа