Вопрос Общественное здоровье и здравоохранения (Социальная медицина и организация здравоохранения) как наука и предмет её изучения
 Скачать 5.08 Mb. Скачать 5.08 Mb.
|
|
Цели, задачи и основные направления концепции развития здравоохранения до 2020 года. Целями развития здравоохранения являются: - прекращение к 2011 году убыли населения Российской Федерации и доведение численности до 145 млн. человек к 2020 году; - увеличение ожидаемой продолжительности жизни населения до 75 лет; - снижение общего коэффициента смертности до 10 (то есть в 1,5 раза по отношению к 2007 году); - снижение показателя младенческой смертности до 7,5 на 1000 родившихся живыми (на 20% по отношению к 2007 г.); - снижение показателя материнской смертности на 100 000 родившихся живыми до 18,6 (на 15,7% по отношению к 2007 г.); - формирование здорового образа жизни населения, в том числе снижение распространенности употребления табака до 25% и снижение потребление алкоголя до 9 л в год на душу населения; - повышение качества и доступности медицинской помощи, гарантированной населению Российской Федерации. Задачами развития здравоохранения являются: - создание условий, возможностей и мотивации населения Российской Федерации для ведения здорового образа жизни; - переход на современную систему организации медицинской помощи; - конкретизация государственных гарантий оказания гражданам бесплатной медицинской помощи; - создание эффективной модели управления финансовыми ресурсами программы государственных гарантий; - улучшение лекарственного обеспечения граждан в амбулаторных условиях в рамках системы обязательного медицинского страхования; - повышение квалификации медицинских работников и создание системы мотивации их к качественному труду; - развитие медицинской науки и инноваций в здравоохранении; - информатизация здравоохранения. 4. В соответствии с результатами анализа состояния здравоохранения в Российской Федерации, а также для достижения поставленных целей предлагаются мероприятия по следующим направлениям: Формирование здорового образа жизни Гарантированное обеспечение населения Российской Федерации качественной медицинской помощью Конкретизация государственных гарантий оказания бесплатной медицинской помощи Стандартизация медицинской помощи Обеспечение населения лекарственными средствами в амбулаторных условиях Финансовое обеспечение оказания гражданам бесплатной медицинской помощи Инновационное развитие здравоохранения Осуществление единой кадровой политики Вопрос 11. Меры изменчивости вариант (амплитуда, среднеквадратичное отклонение, коэффициент вариации). Методика вычисления, сущность, оценка, применение. Средние арифметические величины, взятые сами по себе без дополнительных приемов оценки, часто имеют ограниченное значение, так как они не отражают степени рассеяния (разнообразия) ряда. Одинаковые по размеру средние величины могут быть получены из рядов с различной степенью рассеяния. Средние - это величины, вокруг которых рассеяны различные варианты, и чем ближе друг к другу отдельные варианты, чем меньше рассеяние ряда, тем типичнее средняя величина. Приближенным методом оценки разнообразия ряда может служить определениеамплитуды. Амплитуда - разность между наибольшим и наименьшим значением вариант: А = Vmax – Vmin Но амплитуда не учитывает промежуточные значения вариант внутри ряда, кроме того, ее размеры могут зависеть и от числа наблюдений. Основной мерой оценки разнообразия ряда является среднее квадратическое отклонение (). Вычисление точного значения среднего квадратического отклонения производится по формуле:   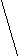  d2р d2р = ± ------------- n Если число наблюдений меньше 30 (малая выборка), то расчет производится по формуле: 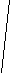  d2р 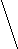 = ± ------------ = ± ------------ n - 1 Для вычисления сигмы необходимо:
3) перемножить квадраты отклонений на частоты (d2р); 4) суммировать произведения квадратов отклонений на частоты; 5) разделить эту сумму на число наблюдений; 6) извлечь из частного квадратный корень. При помощи сигмы можно установить степень типичности средней, пределы рассеяния ряда, пределы колебаний вокруг средней отдельных вариант. Чем меньше сигма, тем меньше рассеяние ряда, тем точнее и типичнее получается вычисленная для этого ряда средняя величина. Применение сигмы дает возможность оценки и сравнения разнообразия нескольких однородных рядов распределения, так как - величина именная, выражается абсолютным числом в единицах изучаемой совокупности (см, кг, мг/л и т.д.). В этом случае принимаются во внимание абсолютные размеры сигмы. Например, при сравнении двух рядов распределения по признаку веса, при условии, что средние будут близки по уровню, но сигма в одном ряду будет ± 5,6 кг., а в другом ± 2,1 кг. - второй ряд менее рассеян, и его средняя более типична. При оценке разнообразия неоднородных рядов (например, таких признаков как вес и рост), непосредственное сравнение размеров сигмы невозможно. В этом случае, для установления степени относительного разнообразия рядов, прибегают к производной величине - коэффициенту изменчивости (вариации), который является относительной величиной, выражается в % и обозначаемому буквой Сv (V). Коэффициент изменчивости получается из процентного отношения сигмы к средней: Cv = ------- · 100% М Например, при изучении физического развития студентов – мужчин 1 курса получены следующие показатели: М (вес) = 67,5 кг.; М (рост) = 178,1 см. Соответственно = ± 2,8 кг. и ± 6,2 см. Среднее квадратическое отклонение по росту более чем в 2 раза превышает сигму по весу. Коэффициент вариации Cv равен: 2,8 кг Cv (по весу) = ------------ · 100% = 4,1% 67,5 кг 6,2 см Cv (по росту) = ------------ · 100% = 3,5% 178,1 см Коэффициент вариации по росту меньше, чем по весу, то есть рост оказался более устойчивым признаком, чем вес. Различают три степени разнообразия коэффициентов вариации: до 10% - слабое разнообразие; 10 – 20 % - среднее разнообразие; более 20 % - сильное разнообразие. Этот же метод вычисления коэффициента разнообразия пригоден и при анализе однородных рядов, у которых средние величины очень разнятся по размеру, а также для оценки изолированного, единичного ряда. Пример вычисления средней арифметической (М); среднего квадратического отклонения (); коэффициента вариации (Cv): Длительность лечения ангины у 45 больных составила: 20, 20, 19, 16, 19, 16, 14, 13, 15, 13, 12, 13, 13, 3, 12, 11, 12, 11, 10, 12, 11, 10, 11, 8, 7, 11, 11, 10, 10, 10, 9, 8, 8, 9, 5, 5, 6, 9, 5, 5, 9, 6, 7, 7, 14, и 15 дней. Первый этап: Строим вариационный ряд, с учетом частоты встречаемости каждой варианты; даем характеристику ряда; находим произведения вариант на соответствующую частоту, суммируем полученные произведения и рассчитываем среднюю арифметическую:
V · p 495 M = ------------ = ------- = 11 дней n 45 Второй этап: рассчитываем d (V-M); d2; d2p. Третий этап: рассчитываем среднее квадратическое отклонение (); коэффициент вариации (Cv): 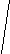  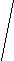  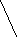 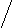  d2р 728 d2р 728 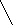 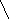 = ± --------- = ± ------ = ± 16,2 = ± 4,02 дня = ± --------- = ± ------ = ± 16,2 = ± 4,02 дняn 45 4,02 Cv = -------- · 100% = ---------- · 100% = 36,5% М 11 Заключение: Средняя длительность лечения ангины в поликлинике составила 11 дней. Средняя является недостаточно типичной для данного ряда, о чем свидетельствует коэффициент вариации, равный 36,5% (большая степень разнообразия признака). Вопрос 12. Средняя ошибка средней арифметической и относительной величин: методика вычисления сущность, оценка. Так называемые средние ошибки являются мерой точности и достоверности любых статистических величин. Под достоверностью статистических показателей (синонимы: существенность, значимость, надежность) понимают доказательность, то есть право на обобщение явления, правомерность распространения выводов и на другие аналогичные явления. Или - степень их соответствия отображаемой ими действительности. Достоверными результатами считаются те, которые не искажают и правильно отражают объективную реальность. Оценить достоверность результатов исследования означает определить, с какой вероятностью возможно перенести результаты, полученные на выборочной совокупности, на всю генеральную совокупность. В большинстве медицинских исследований врачу приходится, как правило, иметь дело с частью изучаемого явления, а выводы по результатам такого исследования переносить на все явление в целом - на генеральную совокупность. Оценка достоверности результатов исследования предусматривает определение: 1) ошибок репрезентативности (средних ошибок средних арифметических и относительных величин) - m; 2) доверительных границ средних (или относительных) величин; 3) достоверности разности средних (или относительных) величин (по критерию t - Стъюдента). Средняя арифметическая величина выборочной совокупности (М) имеет ошибку репрезентативности, которая называется средней ошибкой средней арифметической (mМ) и определяется по формуле: σ m 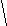 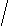  M = ± --------- M = ± ---------n Как видно из этой формулы, между размерами сигмы (отражающей разнообразие явления) и размерами средней ошибки существует прямая связь. Между числом наблюдений и размерами средней ошибки существует обратная связь (пропорциональная не числу наблюдений, а квадратному корню из этого числа). Следовательно, уменьшение величины этой ошибки при определении степени разнообразия (σ) возможно путем увеличения числа наблюдений. При числе наблюдений менее 30 в знаменателе следует взять (n - 1). σ mM = ± --------- 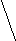 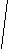  n - 1 На этом принципе основан метод определения достаточного числа наблюдений для выборочного исследования. Относительные величины (Р), полученные при выборочном исследовании, также имеют свою ошибку репрезентативности, которая называется средней ошибкой относительной величины и обозначается mр. Для определения средней ошибки относительной величины (Р) используется следующая формула:     P·q P·q mр = ± ---------- n Где: Р - относительная величина.; q – разность между основанием, на которое рассчитана относительная величина и самой относительной величиной. Если показатель выражен в процентах, то q = 100 – Р: если Р - в промиллях, то q = 1000 - Р, если Р - в продецимиллях, то q = 10.000 - Р, и т.д.; n - число наблюдений. При числе наблюдений менее 30 в знаменатель следует взять (n - 1).     P·q P·q mр = ± ---------- n - 1 Каждая средняя арифметическая или относительная величина, полученная на выборочной совокупности, должна быть представлена со своей средней ошибкой. Это дает возможность рассчитать доверительные границы средних и относительных величин, а также определить достоверность разности сравниваемых показателей (результатов исследования). 2. Определение доверительных границ. Определяя для средней арифметической (или относительной) величины два крайних значения: минимально возможное и максимально возможное, находят пределы, в которых может быть искомая величина генерального параметра. Эти пределы называют доверительными границами. Доверительные границы - границы средних (или относительных) величин, выход за пределы которых вследствие случайных колебаний имеет незначительную вероятность. Вероятность попадания средней или относительной величины в доверительный интервал называется доверительной вероятностью. Доверительные границы средней арифметической генеральной совокупности определяют по формуле: Мген = Мвыб ± t · mM Доверительные границы относительной величины в генеральной совокупности определяют по следующей формуле: Рген = Рвыб ± t · mр Где: Мген и Рген - значения средней и относительной величин, полученных для генеральной совокупности; Мвыб и Рвыб - значения средней и относительной величин, полученных для выборочной совокупности; mM и mр- ошибки репрезентативности выборочных величин; t - доверительный критерий, который зависит от величины безошибочного прогноза, устанавливаемого при планировании исследования. Произведение t · m (Δ) - предельная ошибка показателя, полученного при данном выборочном исследовании. Размеры предельной ошибки зависят от коэффициента t, который избирает сам исследователь, исходя из заданной вероятности безошибочного прогноза. Величина критерия t связана с вероятностью безошибочного прогноза (Р) и числом наблюдений в выборочной совокупности (табл. 4.1). Таблица 4.1 Зависимость доверительного критерия t от степени вероятности безошибочного прогноза Р (при n > 30)
Для большинства медико-биологических и социальных исследований достоверными считаются доверительные границы, установленные с вероятностью безошибочного прогноза = 95% и более. | ||||||||||||||||||||||||||||||||||||||
