Вопрос Общественное здоровье и здравоохранения (Социальная медицина и организация здравоохранения) как наука и предмет её изучения

• Название: Вопрос Общественное здоровье и здравоохранения (Социальная медицина и организация здравоохранения) как наука и предмет её изучения
• Анкор: OZZ.doc
• Дата: 25.11.2017
• Размер: 5.08 Mb.
• Имя файла: OZZ.doc
• Тип: Документы; #10428
• страница: 8 из 29

Вопрос 13.

Достоверность разности средних и относительных величин: методика вычисления, оценка.
В медицине и здравоохранении по разности параметров оценивают средние и относительные величины, полученные для разных групп населения по полу, возрасту, а также групп больных и здоровых и т.д. Во всех случаях при сопоставлении двух сравниваемых величин возникает необходимость не только определить их разность, но и оценить ее достоверность.

Достоверность разности величин, полученных при выборочных исследованиях, означает, что вывод об их различии может быть перенесен на соответствующие генеральные совокупности.

Достоверность разности выборочной совокупности измеряется доверительным критерием, который рассчитывается по специальным формулам для средних и относительных величин.

Формула оценки достоверности разности сравниваемых средних величин:
M₁ - M₂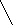

t = ------------------

m₁² + m₂²
Для относительных величин:
Р₁ - Р₂

t = ------------------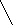




m₁² + m₂²
Где: M₁; M₂ ; Р₁; Р₂- параметры, полученные при выборочных исследованиях;

m₁; m₂ - их средние ошибки;

t - критерий достоверности (Стъюдента).
Разность статистически достоверна при t ≥ 2, что соответствует вероятности безошибочного прогноза, равной 95% и более. Для большинства исследований, проводимых в медицине и здравоохранении, такая степень вероятности является вполне достаточной.

При величине критерия достоверности t < 2 степень вероятности безошибочного прогноза составляет Р < 95%. При такой степени вероятности нельзя утверждать, что полученная разность показателей достоверна с достаточной степенью вероятности. В этом случае необходимо получить дополнительные данные, увеличив число наблюдений.

Иногда при увеличении численности выборки разность продолжает оставаться не достоверной. Если при повторных исследованиях разность остается недостоверной, можно считать доказанным, что между сравниваемыми совокупностями не обнаружено различий по изучаемому признаку.

Например: требуется определить, достоверны ли различия в уровне пепсина в желудочном соке больных гипертериозом и здоровых лиц. Обследуются на пепсин две группы: 49 больных гипертериозом и 50 здоровых людей (контрольная группа). Результаты представлены в таблице 4.3.

Таблица 4.3

Сравнение среднего уровня пепсина в желудочном соке больных гипертериозом и здоровых лиц

Сравниваемые группы	N	М (г%)	m (г%)	t	Уровень вероятности безошибочного прогноза (Р)
Больные гипертериозом	49	1,0	± 0,3	10,0	< 99,9
Здоровые (контрольная группа)	50	4,0	± 0,1

M₁ - M₂

t = ------------------




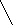m₁² + m₂²
4 - 1

t = ---------------- = 10,0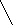




0,3² + 0,1²
Заключение: при гипертериозе наблюдается снижение уровня пепсина, что подтверждается с большой степенью вероятности безошибочного прогноза (Р > 99,9%). Следовательно, снижение уровня пепсина может быть использовано в качестве одного из симптомов для подтверждения диагностики гипертериоза.

Подобным же образом оценивают достоверность разности сравниваемых относительных величин.

Указанная методика оценки достоверности и разности результатов исследования позволяет проводить только сравнение групп по парам, при обязательном наличии обобщающих параметров - средних арифметических или относительных величин и их средних ошибок.
Вопрос 14.

Динамические ряды: определение, виды. Цель и способы выравнивания динамических рядов (показать на условном примере).
Динамический ряд – это совокупность однородных статистических величин, показывающих изменение какого-либо явления на протяжении определенного промежутка времени.

Каждый динамический ряд содержит две составляющие:

1. 
   периоды времени (годы, месяцы, кварталы, недели) или даты;
   
2. 
   величины, характеризующие исследуемый объект за временные периоды или на соответствующие даты, которые называют уровнями ряда.
   

Уровни динамического ряда (ДР) могут быть представлены:

• 
  абсолютными величинами;
  
• 
  относительными величинами;
  
• 
  средними величинами.
  

Динамический ряд, уровни которого представлены абсолютными величинами, называется простым динамическим рядом. Динамический ряд, уровни которого представлены относительными или средними величинами, называется сложным или производным.

По временной составляющей динамический ряд может быть моментным и интервальным.

Моментный динамический ряд состоит из величин, характеризующих явление на какой-то определенный момент – дату (на конец месяца, квартала, года). Например, каждый уровень ряда может характеризовать численность населения, врачей, среднего мед. персонала на конец какого-либо года. Уровни моментного ряда не могут дробиться.

Интервальный динамический ряд состоит из величин, характеризующих явление за какой-то определенный промежуток времени – интервал (неделя, месяц, квартал, год). Например, каждый уровень такого ряда может характеризовать смертность, рождаемость, заболеваемость, среднегодовую занятость койки за какой-то определенный год. Интервальный динамический ряд можно разделить на более дробные периоды или, напротив, укрупнить интервалы.
Цель и способы выравнивания ДР.
Цель. Нередко некоторые уровни в ДР представляют значительные колебания, что затрудняет возможность проследить основную закономерность, свойственную явлению в наблюдаемый период. В этих случаях для выявления общей динамической тенденции рекомендуется произвести выравнивание ДР.

Методы:

• 
  укрупнение интервала;
  
• 
  вычисление групповой средней;
  
• 
  вычисление скользящей средней.
  

1. 
   Укрупнение интервала – производят путем суммирования данных за ряд смежных периодов.
   

Сезонные колебания случаев ОКИ в районе N (по месяцам 2010 г.)

Число случаев	Месяцы 2010 г.
По месяцам	1	2	3	4	5	6	7	8	9	10	11	12	Всего
	120	190	130	380	230	280	530	380	390	230	140	250	3250
По кварталам	440			890			1300			620			3250

Таким образом, после укрупнения интервалов по кварталам года выявлена определенная тенденция: наибольшее количество заболеваний ОКИ приходится на летне-осенний период.

2. 
   Групповая средняя – вычисляется как средняя арифметическая уровней, составляющих укрупненный интервал.
   

Динамика процента расхождения клинических и патологоанатомических диагнозов в больнице города N за 2005-2010 гг.

Годы	2005	2006	2007	2008	2009	2010
Процент расхождения диагнозов	10,0%	10,2%	9,2%	9,6%	9,5%	8,9%
Групповая средняя	10,1%		9,4%		9,2%

Уровни ДР, представленные в таблице имеют волнообразные колебания. Выравнивание ряда путем вычисления групповой средней позволило выявить четкую тенденцию к постепенному снижению процента расхождений диагнозов в областной больнице.

3. 
   Скользящая средняя – вычисляется как средняя величина из данного уровня и двух соседних с ним. При этом временной интервал ДР не укрупняется и остается прежним, а значение каждого уровня ряда заменяется на среднюю величину из данного уровня и двух соседних с ним (предыдущего и последующего). Таким образом, данный метод исключает из анализа значения первого и последнего уровней.
   

Динамика процента расхождений клинического и патологоанатомического диагнозов в больнице города N за 2005-2010 гг.

Годы	2005	2006	2007	2008	2009	2010
Процент расхождения адиагнозов	10,0%	10,2%	9,2%	9,6%	9,5%	8,9%
Скользящая средняя	-	9,8%	9,7%	9,4%	9,3%	-

Ряд, выровненный с помощью скользящей средней, более плавно иллюстрирует общую тенденцию: постепенное уменьшение показателей частоты расхождения диагнозов.
Вопрос 15.

Динамические ряды. Показатели динамики изучаемого явления: наименование, методика расчета, сущность (показать на условном примере).
Для анализа ДР лучше всего его изобразить графически. ДР можно подвергнуть преобразованиям, целью которых является выявление особенностей изучаемого процесса, а также достижение наглядности в характеристике того или иного явления.

Для определения тенденции изучаемого явления рассчитывают следующие показатели ДР:

1. 
   Абсолютный прирост (убыль) – это разность между последующим и предыдущим уровнем (измеряется в тех же единицах, в которых представлены уровни ряда).
   
2. 
   Темп прироста (убыли) – это отношение абсолютного прироста (убыли) каждого последующего уровня к предыдущему, принятому за 100%. Темп прироста показывает на сколько процентов увеличился (снизился) последующий уровень по сравнению с предыдущим.
   

Темп прироста = 9Абсолютный прирост/Предыдущий уровень )x 100%

3. 
   Темп роста (убыли) – это отношение каждого последующего уровня к предыдущему, принятому за 100%, т.е. темп роста показывает сколько процентов от предыдущего уровня составляет последующий уровень.
   

Темп роста = (Последующий уровень/ Предыдущий уровень) х 100%

4. 
   Абсолютное значение 1% прироста – это отношение абсолютного прироста (убыли) к темпу прироста.
   

Абсолютное значение 1% прироста = Абсолютный прирост/Темп прироста

5. 
   Показатель наглядности – это отношение каждого уровня ряда к одному из них (чаще первому или последнему), принятому за 1 или за 100%.
   

Пример расчета показателей.

Годы	Уровень заболеваемости (на 100000 населения)	Метод вычисления групповой средней	Метод вычисления скользящей средней
2000	2,0	1,8	-
2001	1,5		1,9
2002	2,3	2,1	1,9
2003	1,8		2,0
2004	2,0	2,3	2,1
2005	2,5		2,2
2007	2,2	2,5	2,5
2008	2,8		2,3
2009	2,0	2,5	2,6
2010	2,9		-

1. 
   Рассчитаем показатели динамического ряда.
   
   1. 
      Абсолютный прирост (убыль) рассчитаем как разность между последующим и предыдущим уровнем.
      

Пример расчета для 2001 г.: 1,5 – 2 = -0,5

2. 
   Темп прироста (убыли) рассчитаем как отношение абсолютного прироста (убыли) каждого последующего уровня к предыдущему, принятому за 100%.
   

Пример расчета для 2001 г.: (-0,5) х 100% : 2 = -25%

3. 
   Темп роста (убыли) рассчитаем как отношение каждого последующего уровня к предыдущему, принятому за 100%.
   

Пример расчета для 2001 г.: 1,5 х 100% : 2 = 75%

4. 
   Абсолютное значение 1% прироста (убыли) рассчитаем как отношение абсолютного прироста (убыли) к темпу прироста.
   

Пример расчета для 2001 г.: (-0,5) : (-25) = 0,02

5. 
   Показатель наглядности рассчитаем как отношение каждого уровня ряда к одному из них (чаще первому или последнему), принятому за 100%.
   

Пример расчтеа для 2001 г.: 1,5 х 100% : 2 = 75%

Вопрос № 16








Вопрос № 17













Вопрос № 18





Вопрос № 20





Вопрос № 19