Рабочая книга социолога. Вторая структура социологического знания общая социологическая теория

• Название: Вторая структура социологического знания общая социологическая теория
• Анкор: Рабочая книга социолога.doc
• Дата: 19.11.2017
• Размер: 3.63 Mb.
• Имя файла: Рабочая книга социолога.doc
• Тип: Глава; #10295
• Категория: Социология. Политология
• страница: 16 из 38

Меры взаимозависимости для интервального уровня измерения. Наиболее широко известной мерой связи служит коэффициент кор­реляций Пирсона (или, как его иногда называют, коэффициент кор­реляции, равный произведению моментов). Одно из важнейших предположений, на котором покоится использование коэффициента г, состоит в том, что регрессионные уравнения для изучаемых переменных имеют линейную форму²³, т. е.



где у — среднее арифметическое для переменной у; х — среднее арифметическое для переменной х; b₁и b₂ - некоторые коэффи­циенты.

Поскольку вычисление коэффициента корреляции и коэффици­ентов регрессии b₁ и b₂ проводится по схожим формулам, то, вычисляя r, получаем сразу же и приближенные регрессионные модели²⁴.

 



Выборочные коэффициенты регрессии и корреляции вычисляются по формулам



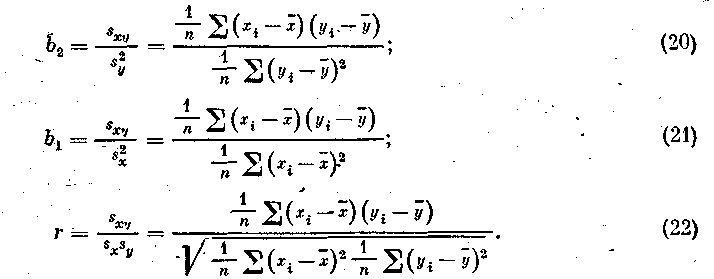
Здесь s²_x —дисперсия признака х; s²_x— дисперсия признака у.Величина s_xy, называется ковариацией х и у.

Расчет r для не с группированных данных. Для вычислительных целей эти выражения в случае не сгруппированных данных можно переписать в следующем виде:



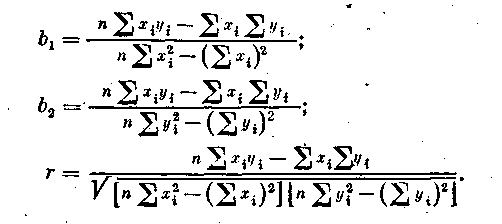
Рассчитаем коэффициент корреляции и коэффициенты регрессии для данных табл. 7:



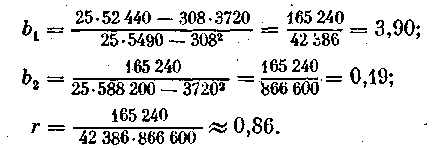
Тогда уравнение регрессии имеет вид



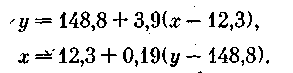
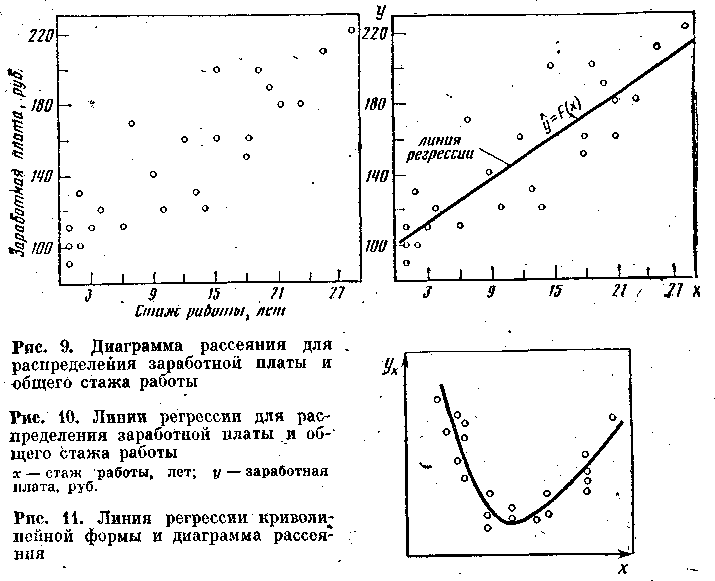
Линии регрессии y = F(x) изображены на рис. 10-. Отсюда вид­но, что между заработной платой и общим стажем работы сущест­вует прямая зависимость: по мере увеличения общего стажа рабо­ты на предприятии растет и заработная плата. Величина коэффи­циента корреляции довольно большая и свидетельствует о положи­тельной связи между переменными величинами. Следует отметить, что вопрос о том, какую переменную в данном случае принимать в качестве зависимой величины, а какую — в качестве независимой, исследователь решает на основе качественного анализа и профес­сионального опыта. Коэффициент корреляции по определению яв­ляется симметричным показателем связи: r_xy = r_yx. Область возмож­ного изменения коэффициента корреляции г лежит в пределах от +1 до —1.

Вычисление r для сгруппированных данных. Для сгруппирован­ных данных примем ширину интервала по каждой переменной за единицу (если по какой-либо переменной имеются неодинаковые размеры интервала, то возьмем из них наименьший). Выберем так­же начало координат для каждой переменной где-нибудь возле среднего значения, оцененного на глаз.

Для условных данных, помещенных в табл. 8, за нулевую точ­ку отсчета выберем значение у, равное 64, а по x — значение 134,5.

Тогда коэффициент корреляции определяется по следующей формуле:





 

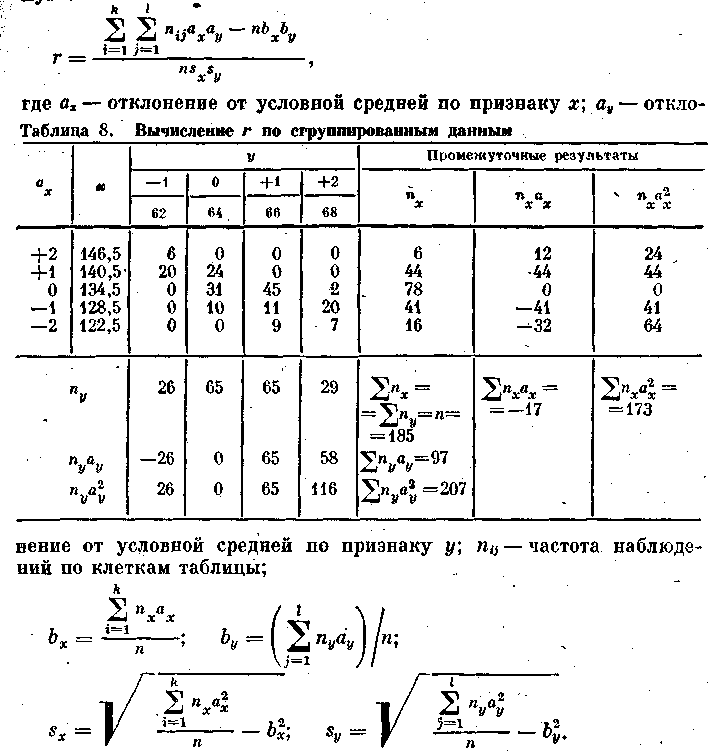
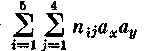
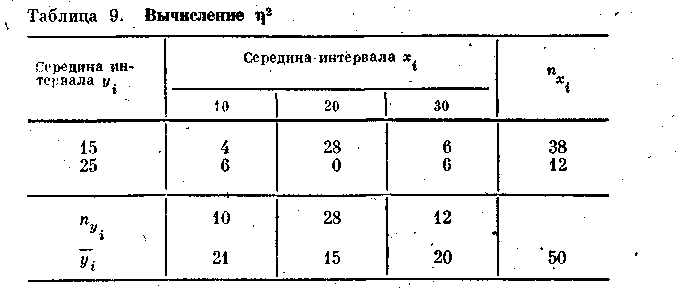
Для вышеприведенного примера порядок вычислений представлен в табл. 9. Для определения Sn_ija_xb_y вычислим последовательно все произведения частоты в каждой клетке таблицы на ее коор­динаты. Так





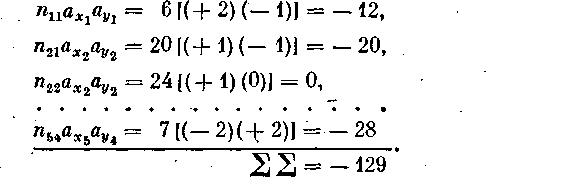
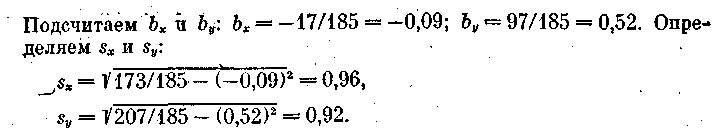
В соответствии с формулой вычисляем



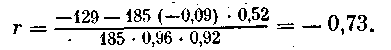
Таким образом, величина связи достаточно велика, как, впрочем, и следовало ожидать на основе визуального анализа таблицы.

Статистическая значимость r. После вычисления коэффициента корреляции возникает вопрос, насколько показателен этот коэффи­циент и не обусловлена ли зависимость, которую он фиксирует, случайными отклонениями. Иначе говоря, необходимо проверить гипотезу о том, что полученное значение r значимо отличается от 0.

Если гипотеза H₀ (r = 0) будет отвергнута, говорят, что величи­на коэффициента корреляции статистически значима (т. е. эта ве­личина не обусловлена случайностью) при уровне значимости a.

Для случая, когда п < 50, применяется критерий t, вычисляе­мый по формуле



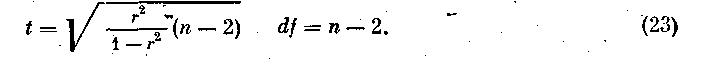
Распределение t дано в табл. В приложения.

Если п > 50, то необходимо использовать Z-критерий



В табл. А приложения приведены значения величины Z_Kpдля соответствующих a.

Вычислим величину Z для коэффициента корреляции по табл. 7 (вычисление проделаем лишь для иллюстрации, так как число на­блюдений п — 25 и нужно применять критерий t). Величина r (см. табл. 7) равна 0,86. Тогда



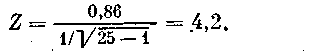
Для уровня значимости a = 0,01 Z_Kp = 2,33 (см. табл. А прило­жения).

Поскольку Z > Z_Kp, мы должны констатировать, что коэффици­ент корреляции г = 0,86 значим и лишь в 1 % случаев может ока­заться равным нулю. Аналогичный результат дает и проверка по критерию t для а = 0,01 (односторонняя область); t_кр— 2,509, tвы­борочное равно 8,08.

Другой часто встречающейся задачей, является проверка равен­ства на значимом уровне двух коэффициентов корреляции. i = г₂ при заданном уровне а, т. е. различия между r₁ и r₂ обусловлены лишь колебаниями выборочной совокупности.

Критерий для проверки значимости следующий:



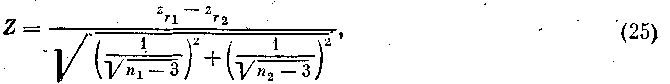
где значения z_rj и z_rнаходят по табл. Д приложения для r₁ и r₂.

Значения Z_Кp определяют по табл. А. приложения аналогично вышеприведенному примеру.

Частная и множественная регрессия и корреляция. Ранее нами было показано, как можно по опытным данным найти зависимость одной переменной от другой, а именно как построить уравнение регрессии вида у = а + bх. Если исследователь изучает влияние не­скольких переменных х₁, х₂, ..., х_k результатирующий признак y, то возникает необходимость в умении строить регрессионное урав­нение более общего вида, т. е.



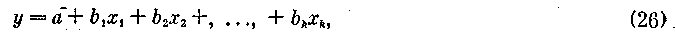
где a, b₁,. b₂, ..., b_k— постоянные коэффициенты, коэффициенты регрессии.

В связи с уравнением (26) необходимо рассмотреть следующие вопросы: а) как по эмпирическим данным вычислить коэффициенту регрессии а, b₁, b₂…b_к ; б)какую интерпретацию можно припи­сать этим коэффициентам; в) оценить тесноту связи между у и каждым из Xi в отдельности (при элиминировании действия остальных); г) оценить тесноту связи между у и всеми переменными х₁, ..., x_кв совокупности.

Рассмотрим этот вопрос на примере построения двухфакторного регрессионного уравнения. Предположим, что изучается зависимость недельного бюджета свободного времени (у) от уровня образования (х_i) и возраста (х₂) определенной группы трудящихся по данным выборочного обследования. Будем искать эту зависимость в виде линейного уравнения следующего вида:

При расчете коэффициентов уравнения множественной регрессии полезно преобразовать исходные эмпирические данные следующим образом. Пусть в результате обследования п человек получены эм­пирические значения, сведенные в следующую таблицу (в каждом столбце представлены не сгруппированные данные):



Каждое значение переменной в таблице преобразуем по формулам





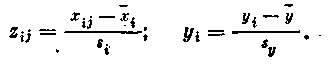
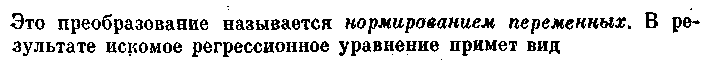
Коэффициенты с₁ и с_гнаходятся по следующим формулам



с₁ и с₂ называются стандартизированными коэффициентами регрес­сии. Следовательно, зная коэффициенты корреляции между изучае­мыми признаками, можно подсчитать коэффициенты регрессии. Подставим конкретные значения r_ij из следующей таблицы²⁵;



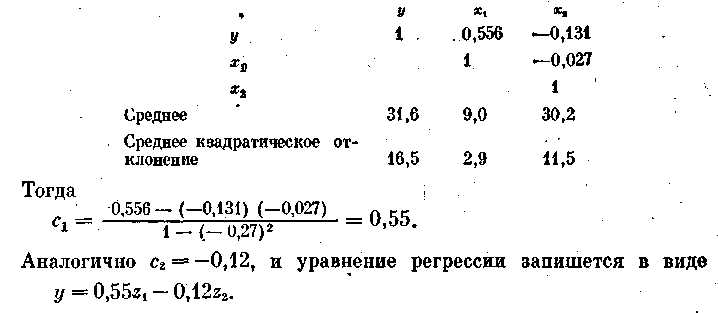
Коэффициенты исходного регрессионного уравнения b₀, b₁ и b₂ на­ходятся по формулам



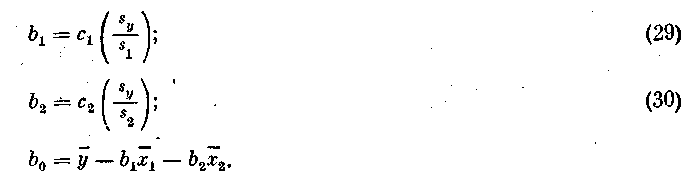
Подставляя сюда данные из вышеприведенной таблицы, получим b₁= 3,13; b₂= -0,17; b₀= - 8,56.

Как же следует интерпретировать это уравнение? Например, значение b₂показывает, что в среднем недельный бюджет свободного времени при увеличении возраста на один год и при фиксированном признаке Xi уменьшается на 0,17 час. Аналогично интер­претируется b₁. (Исходные эмпирические данные можно изобразить на диаграмме рассеяния аналогично тому, как это сделано на рис. 10, но уже в трехмерном пространстве (у, x_t, х₂).

Коэффициенты х₁ и х₂ можно в то же время рассматривать и как показатели тесноты связи между переменными у и, например, Xi при постоянстве х_г.

Аналогичную интерпретацию можно применять и к стандарти­зированным коэффициентам регрессии с_i. Однако поскольку c_iвы­числяются исходя из нормированных переменных, они являются безразмерными и позволяют сравнивать тесноту связи между пере­менными, измеряемыми в различных единицах. Например, в выше­приведенном примере Xi измеряется в классах, a x₂ — в годах. C₁и с₂ позволяют сравнить, насколько z₁ теснее связан с у, чем х_г²⁶.

Поскольку коэффициенты b_iи с_i измеряют частную односторон­нюю связь, возникает необходимость иметь показатель, характери­зующий связь в обоих направлениях. Таким показателем является частный коэффициент корреляции



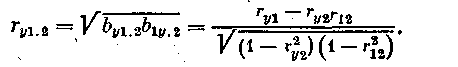
Для рассматриваемого примера r_y1.2 = 0,558, r_у2.1 i = —0,140.

Для любых трех переменных x₁, х₂, х₃частный коэффициент корреляции между двумя из них при элиминировании третьей стро­ится следующим образом:



Аналогично можно определить и частные коэффициенты корре­ляции для большего числа переменных (r₁₂, ₃₄ ...). Однако ввиду громоздкости вычисления они применяются достаточно редко.

Для характеристики степени связи результатирующего признака у с совокупностью независимых переменных служит множествен­ный коэффициент корреляции R²_y, который вычисляется по формуле (иногда он выражается в процентах)



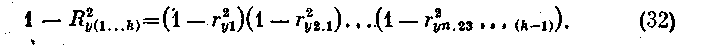
Так, для вышеприведенного примера он равен



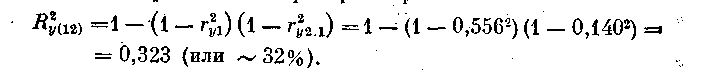
Множественный коэффициент корреляции показывает, что включе­ние признаков х₁и х₂в уравнение



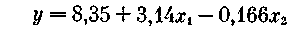
на 32% объясняет изменчивость результатирующего фактора. Чем больше R_t, тем полнее независимые переменные х₂..., x_kописы­вают признак у. Обычно служит критерием включения или ис­ключения новой переменпой в регрессионное уравнение. Если Л мало изменяется при включении новой переменной в уравнение, то такая переменная отбрасывается.

Корреляционное отношение. Наиболее общим показателем связи при любой форме зависимости между переменными является корре­ляционное отношение h². Корреляционное отношение h²_у/хопреде­ляется через отношение межгрупповой дисперсии к общей диспер­сии по признаку у:



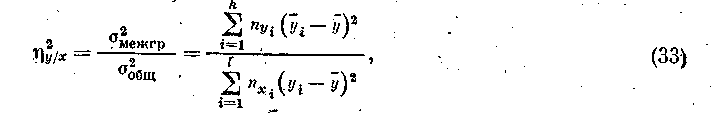
где у_i — среднее значение i-ro y-сечения (среднее признака у для объектов, у которых x=x_i, т. е. столбец «г»); x_i —среднее значе­ние i-го x-сечения т. е. строка «i» n_yi —число наблюдений в y сечении; n_Xi— число наблюдений в x-сечении; у — среднее зна­чение у.

Величина h²_у/хпоказывает, какая доля изменчивости значений у обусловлена изменением значения х. В отличие от коэффициента корреляции h²_у/х не является симметричным показателем связи, т. е, h²_у/х не равно h²_х/y. Аналогично определяется корреляционное отношение х по у²⁷.

Пример. По данным таблицы сопряженности (табл. 9) найдем h²_у/х. Вычислим общую среднюю



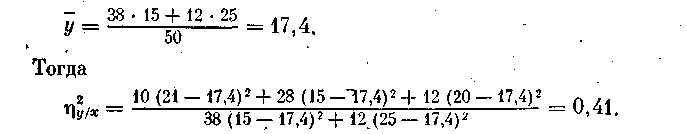
Сравнение статистических показателей r и h²_у/х. Приведем сравнительную характеристику коэффициента корреляции (будем срав­нивать r²) и корреляционного отношения h²_у/х.

а) r² = 0, если x и у независимы (обратное утверждение не­верно);

б) r² =h²_у/х =1 тогда и только тогда, когда имеется строгая ли­нейная функциональная зависимость у от х.

в) r² = r\y/_x<i тогда и только тогда, когда регрессия х и у стро­го линейна, но нет функциональной зависимости;

г) r² <h²_у/х< 1 указывает на то, что нет функциональной зави­симости и существует нелинейная кривая регрессии.



Коэффициенты взаимозависимости для порядкового

уровня из­мерения.

К этой группе относятся коэффициенты ранговой корреля­ции Спирмена r_а, Кендалла t и g. Коэффициенты ранговой корре­ляции используются для измерения взаимозависимости между ка­чественными признаками, значения-которых могут быть упорядоче­ны или проранжированы по степени убывания (или нарастания) данного качества у исследуемых социальных объектов.

Коэффициент ранговой корреляции Спирмена r_s. Этот коэффи­циент вычисляется по следующей формуле:



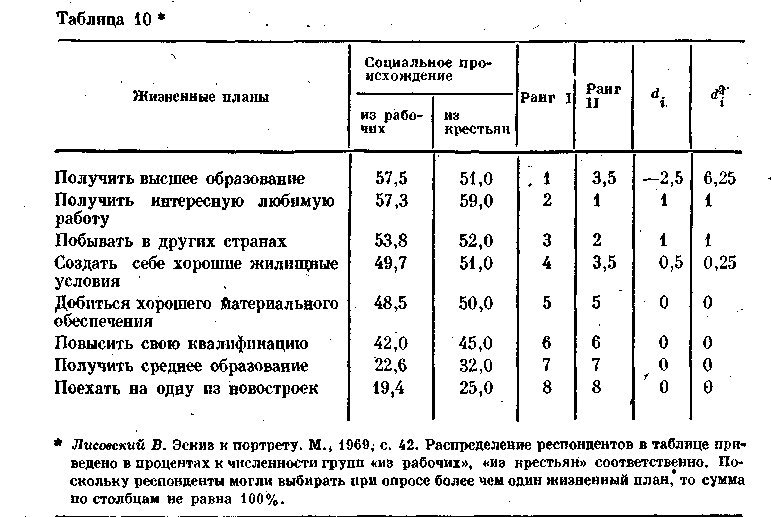
где di = i — ki— разность между i-ми парами рангов; I — число сопоставляемых пар рангов. Величина r_s может изменяться в преде­лах от +1 до — 1, когда два ряда проранжированы в одном поряд­ке. При полном взаимном беспорядочном расположении рангов г, равен нулю. Пример. По данным табл. 10 выясним, в какой степени связаны жизненные планы детей, отличающихся по социальному происхождению. Для этого проранжируем значения процентных распределений для каждой из двух групп детей.

В графе «из крестьян» (табл. 10) встречаются два одинаковых числа (51, 0). В подобных случаях обоим числам присваивают ранг, равный среднему арифметическому из этих рангов, т. е. (3 + 4)/2 = 3,5. Подставляя промежуточные величины, вычисленные в табл. 10, в формулу (34), находим²⁸



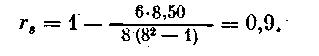
Такую величину r, можно интерпретировать как высокую сте­пень связи между жизненными планами детей рабочих и крестьян. Однако большая величина г, не должна скрывать тот факт, что жизненные планы молодежи в табл. 10 распадаются на две груп­пы. Для одной группы (нижняя часть таблицы) ранги полностью совпадают, а для другой (верхняя часть) — нет.



Если подсчитать r_s, для каждой группы отдельно, то в первом случае, очевидно, r_s= 1, а во втором r_s=0,15, но статистически не­значимо отличается от 0.

Значимость коэффициента корреляции Спирмена для l < 100 можно определить по табл. Г приложения, где приведены крити­ческие величины r_s.

Если l> 100, то критические значения находятся по табл. А формуле



Например, возвращаясь к данным табл. 10, где l< 100, по табл. Г приложения найдем, что для того, чтобы rбыл значим на уровне 0,01, он должен быть равен или превосходить 0,833. Эмпирическое значение r, = 0,9, и поэтому делается вывод, что имеется значимая связь между предпочтениями жизненных планов двух групп рес­пондентов. Аналогичным образом легко убедиться, что r_s, = 0,15 при l= 4 статистически незначим.

Коэффициент ранговой корреляции t Кендалла. Подобно r_s ко­эффициент Кендалла используется для измерения взаимосвязи между качественными признаками, характеризующими объекты од­ной и той же природы, ранжированные по одному и тому же критерию, т изменяется от +1 до —1. Для расчета t₀ используется формула



Как вычисляется S, поясним на примере данных табл. 10.

Таблица упорядочена так, что в графе «Ранг I» ранги располо­жились в порядке возрастания их значений. Берем значение ранга, стоящего в графе «Ранг II» на первом месте, 3,5; из расположен­ных ниже данного ранга семи других четыре значения его превы­шают, а два — меньше его. Число 4 записывается в графу S_i , a 2 в колонку S_i. Аналогичный подсчет делается для второго ранга со значением 1. Число рангов, расположенных ниже данного значения и превышающих его, равно 6, а число рангов, меньших данного,— 0 и т. д. Остальные вычисления ясны из следующей таблицы:



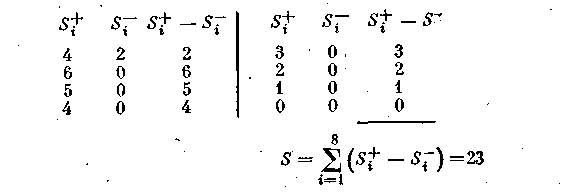
Тогда, подставив соответствующие значения в формулу (36), по­лучим



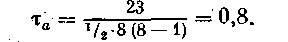
Таким образом, t_а дает более осторожную оценку для степени связи двух признаков, чем r_s.

При расчете t не учитывались равные ранги. Например, в табл. 10 имеются два равных ранга со значением 3,5. Если число равных рангов велико, то необходимо вычислить т по следующей формуле:



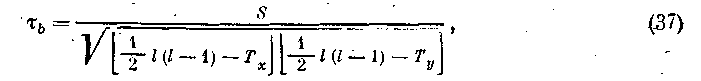
где Т_х= i/2Zt_x(t_x—i) (t_x—число равных рангов по первой пере­менной); Ту=i/2Zt_y(t_v—i) (t_y — число равных рангов по второй: переменной).

Для предыдущего примера t_x= 1, t_v=2,тогда Т_х = 0, T_y = 1.

Значимость коэффициента корреляции Кендалла t при l > 10 определяется по формуле



Гипотеза о том, что t_а = 0, будет отвергнута для данного а, если |Z|>Z_кр(a/2).

Для вышеприведенного примера ,



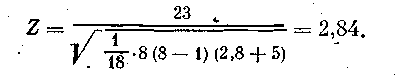
По табл. А приложения для а = 0,05 находим Z_Kp(a/2), равное 1,96. Поскольку расчетное значение 2 = 2,84 и, следователыю, боль­ше Z_кр, заключаем с вероятностью 95%, что t не равно 0.

Коэффициенты корреляции Спирмена и Кендалла используются как меры взаимозависимости между рядами рангов, а не как меры связи между самими переменными. Так, в табл. 10 ранги отражают иерархию жизненных планов, но совершенно не говорят о том, что дети рабочих почти в равной мере хотят получить как высшее образование, так и интересную работу (разница 0,2%), а дети крестьян в большей степени стремятся к высшему образованию (разница 8%). Кроме того, какая-нибудь из групп респондентов может считать, что выделенные категории вообще не отражают их жизненных планов, по проранжировали предложенные варианты. Если для целей исследования можно предположить эти моменты несущественными, то оправданно применение ранговой корреляции.

Коэффициенты Спирмена и Кендалла обладают примерно оди­наковыми свойствами, но в случае многих рангов, а также при введении дополнительных объектов в ходе исследования имеет определенные вычислительные преимущества²⁹.

Другая мера связи между двумя упорядоченными переменны­ми — g. Она, так же как и предыдущие коэффициенты, изменяется

от +1 до — 1 и может быть подсчитана при любом числе связанных рангов. Формула для вычисления g записывается в виде



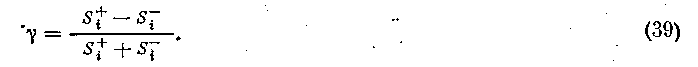
Для иллюстрации правил вычисления 5, по сгруппированным дан­ным обратимся к примеру (табл. 11).



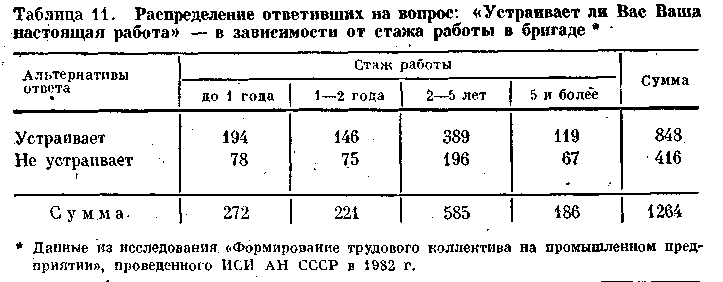
Процесс вычисления S⁺и S наглядно представлен на схеме

(схема 2).



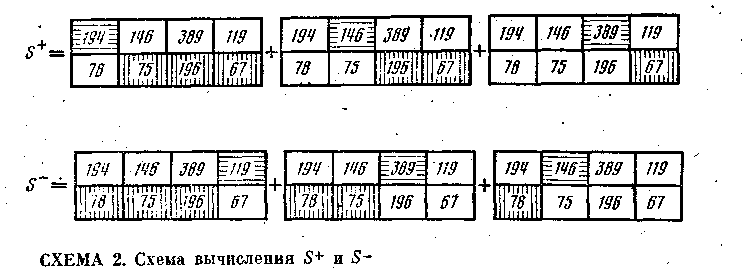
Так:



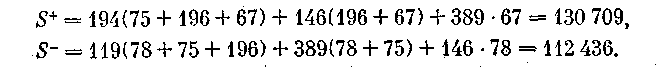
Подставляя эти величины в формулу для g, находим



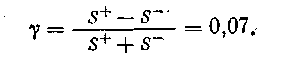
Проверку статистической значимости проводят по формуле



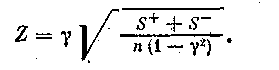
Гипотеза Н₀оравенстве нулю коэффициента отвергается, если Z>Z_Kр(a/2). Для наших данных



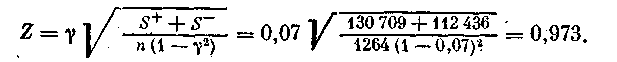
Для а = 0,05 по табл. А приложения Z_Kp(a/2) = 1,96. Таким обра­зом, Z < Z_Kp, и, следовательно, у нас нет оснований отвергнуть гипотезу Н₀ : g= 0, т. е. лишь в 5 % случаев следует ожидать, что gбудет отличен от нуля.

Множественный коэффициент корреляции W. Этот коэффициент, иногда называемый коэффициентом конкордации, используется для измерения степени согласованности двух или нескольких рядов проранжированных значений переменных.

Коэффициент W вычисляется по формуле



Значимость полученной величины W для и > 7 проверяется по критерию c²:



со степенью свободы п — 1. Для примера c^{2 =} 10,133, степень свобо­ды (n— 1)=4. Для a= 0,05 из табл. Б приложения находим c² = 9,488. Поскольку наблюдаемое значение c² больше критической точки, отвергаем гипотезу о том, что не существует значимой связи между рассматриваемыми переменными³⁰.