|
|
8 сынып алгебра қмж 1-тоқсан. 1 токсан. за мерзімді жоспарды тарауы Кні
Сабақтың барысы
Сабақтың кезеңі
|
Педагогтың әрекеті
|
Оқушының әрекеті
|
Бағалау
|
Ресурстар
|
Сабақтың басы
|
Жай бөлшекті периодты ондық бөлшекке айналдыру үшін алымын бөліміне бөлу арқылы шектеулі немесе шектеусіз ондық бөлшекке келтіріп алады, содан кейін қайталанатын санды немесе сандар тобын теңдіктен кейін жақшаға алу арқылы периодты ондық бөлшек түрінде көрсетіп жазады..Мысалы: 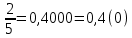 ; ; 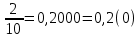 ; ; 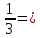 0,3333… 0,3333…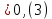 ; ; 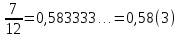 ,т.с.с. ,т.с.с.
Кез келген шектеусіз периодты ондық бөлшекті жай бөлшек түріне келтіруге болады: 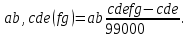 Яғни периодты ондық бөлшектің бүтін бөлігін өзгертпей сол қалпында қалдырып, әрі қарай , бөлшек сызығының бөліміне периодтық бөлігінде қанша цифр болса, сонша 9 , үтір мен периодтық бөліктің арасында қанша цифр болса, сонша 0 жазады. Яғни периодты ондық бөлшектің бүтін бөлігін өзгертпей сол қалпында қалдырып, әрі қарай , бөлшек сызығының бөліміне периодтық бөлігінде қанша цифр болса, сонша 9 , үтір мен периодтық бөліктің арасында қанша цифр болса, сонша 0 жазады.
Мысал1. Периодты ондық бөлшектерді жай бөлшектер түрінде жазыңыз:
1) 0,(31); 3) 1,4(83);
2) 10,20(7); 4) 0,0(123);
|
Шешуі:
1) 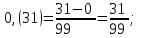 3) 3) 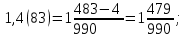
2) 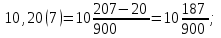 4) 4) 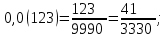
|
Оқушылардың белсенділіген байланысты бағаланады.
|
Презентация
|
Сабақ ортасы
|
Мысал2.Сандарды салыстырыңыз:
1) 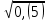 және және 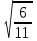 4) 4) 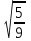 және және 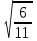
2) 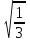 және және 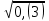 5) 5) 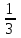 және және 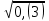
3) 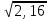 және және 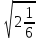 6) 6) 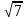 және және 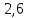
|
Шешуі:
1) 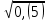 > >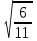 4) 4) 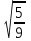 > >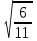
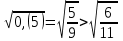 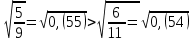
2) 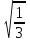 = =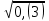 5) 5) 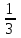 < <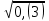
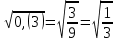 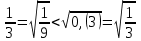
3) 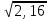 < <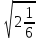 6) 6) 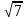 > >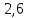
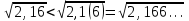 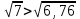
|
Оқушылардың белсенділіген байланысты бағаланады.
|
https://bilimland.kz/kk/subject/algebra/8-synyp/kvadrat-tubir-kvadrat-tubirding-zhuyq-manderi?mid=%info%
|
Сабақ соңы
|
Мысал3.Дөңгелектің ауданы 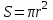 (мұндағы r-шеңбердің радиусы) формуласы немесе (мұндағы r-шеңбердің радиусы) формуласы немесе 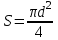 (мұндағы d-шеңбердің диаметрі) формуласы бойынша есептеліп шығарыла алады: (мұндағы d-шеңбердің диаметрі) формуласы бойынша есептеліп шығарыла алады:
а) r-дің S-ке тәуелділігін;
б) d-нің S-ке тәуелділігін формуламен жазыңыз.
|
Шешуі:
а) 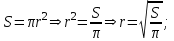
б) 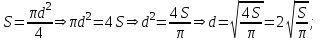
|
Оқушылардың белсенділіген байланысты бағаланады.
|
|
Ұзақ мерзімді жоспардың тарауы: Квадрат түбір және иррационал өрнек
|
Күні:
|
Мектеп: Н.Ильясов атындағы № 9 мектеп-гимназия
|
Мұғалімнің аты-жөні: Сардарбекоа Г.Б.
|
Сынып: 8 «А»
|
Қатысқандар:
|
Қатыспағандар:
|
Сабақтың тақырыбы
|
Құрамында квадрат түбірлері бар өрнектерді түрлендіру
|
Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме)
|
8.1.2.5
құрамында түбір таңбасы бар өрнектерді түрлендіруді орындау;
|
Сабақтың мақсаты
|
Есеп шығаруда құрамында түбір таңбасы бар өрнектерді түрлендіруді орындау;
|
Сабақтың барысы
Сабақтың кезеңі
|
Педагогтың әрекеті
|
Оқушының әрекеті
|
Бағалау
|
Ресурстар
|
Сабақтың басы
|
Алдыңғы сабақтардаквадрат түбірлердің келесі жеті қасиеттеріне толық тоқталған едік:
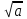 өрнегінің анықталу облысы теріс емес нақты сандар жиыны: өрнегінің анықталу облысы теріс емес нақты сандар жиыны: 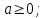
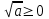 - арифметикалық түбір теріс емес; - арифметикалық түбір теріс емес;
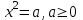 теңдеуінің екі түбірі бар: теңдеуінің екі түбірі бар: 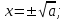
кез келген 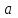 саны үшін саны үшін 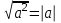 теңдігі орындалады. теңдігі орындалады.
көбейтіндінің квадрат түбірі көбейткіштердің квадрат түбірлерінің көбейтіндісіне тең, яғни егер 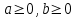 болса, онда болса, онда 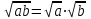 . .
бөліндінің квадрат түбірі квадрат түбірлердің қатынасына тең, яғни егер 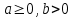 болса, онда болса, онда 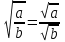 теңдігі орындалады. теңдігі орындалады.
дәреженің түбірі түбірдің дәрежесіне тең, яғни, егер 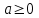 болса, онда кез келген натурал болса, онда кез келген натурал 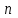 саны үшін саны үшін 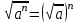 теңдігі орындалады. теңдігі орындалады.
Салдар. Егер 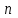 жұп сан болса, онда жұп сан болса, онда 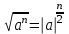 теңдігі орындалады. теңдігі орындалады.
Енді осы қасиеттерді пайдаланып, көбейткішті квадрат түбір белгісінің алдына шығарып және көбейткішті квадрат түбір белгісінің астына алайық.
көбейткішті квадрат түбір белгісінің алдына шығару үшін,квадрат түбір таңбасының астындағы өрнекті түрлендіріп, оны бір көбейткіші қандай да бір өрнектің квадраты болатындай етіп көбейтіндіге жіктейміз. Сосын, көбейткішті түбір таңбасының алдына шығарамыз.
|
Мысалы1.Көбейткішті түбір таңбасының алдына шығару:
1)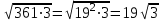 ; ;
2)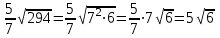 ; ;
3) 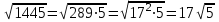
4) 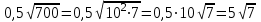
5) 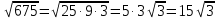
|
Оқушылардың белсенділіген байланысты бағаланады.
|
Презентаци
https://bilimland.kz/kk/subject/algebra/8-synyp/kobejtkishti-kvadrat-tubir-tangbasynyng-aldyna-shyharu?mid=%info%(я
|
Сабақ ортасы
|
көбейткішті квадрат түбір белгісінің астына алу үшін, квадрат түбірдің қасиетіне сүйене отырып, осы көбейткіштің квадратын түбір таңбасының астына енгізу керек, яғни кез келген 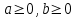 үшін үшін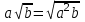 теңдігі орындалады. теңдігі орындалады.
Мысал2. Көбейткішті түбір таңбасының астына алу:
а)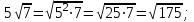
b)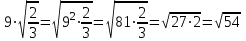 ; ;
c) 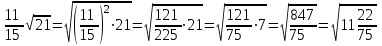
6
|
Мысал3.Көрсетілген амалды орындаңыз:
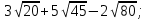
Шешуі:
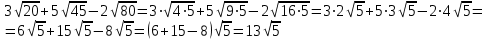
Жауабы: 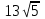
|
Оқушылардың белсенділіген байланысты бағаланады.
|
https://bilimland.kz/kk/subject/algebra/8-synyp/kobejtkishti-kvadrat-tubir-tangbasynyng-aldyna-shyharu?mid=%info%(
|
Сабақ соңы
|
Мысал4.Түбірдің мәнін табу(қысқаша көбейту формулалары көмегі арқылы):
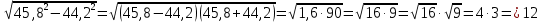 . .
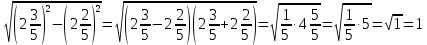 . .
Мысал5.Есептеңіз:
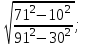
|
Шешуі:
Қысқаша көбейту формулаларын пайдаланып, көбейткіштерге жіктеп ықшамдайық. Сосын, бөлшектің алымы мен бөлімін 61-ге қысқартайық. (4), (6) қасиеттерді пайдалана отырып, жауабын аламыз.
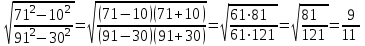 Жауабы: Жауабы: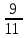
|
Оқушылардың белсенділіген байланысты бағаланады.
|
https://bilimland.kz/kk/subject/algebra/8-synyp/kobejtkishti-kvadrat-tubir-tangbasynyng-aldyna-shyharu?mid=%info%(
|
Ұзақ мерзімді жоспардың тарауы: Квадрат түбір және иррационал өрнек
|
Күні:
|
Мектеп: Н.Ильясов атындағы № 9 мектеп-гимназия
|
Мұғалімнің аты-жөні: Сардарбекоа Г.Б.
|
Сынып: 8 «А»
|
Қатысқандар:
|
Қатыспағандар:
|
Сабақтың тақырыбы
|
Құрамында квадрат түбірлері бар өрнектерді түрлендіру
|
Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме)
|
8.1.2.5
құрамында түбір таңбасы бар өрнектерді түрлендіруді орындау;
|
Сабақтың мақсаты
|
Есеп шығаруда құрамында түбір таңбасы бар өрнектерді түрлендіруді орындау;
| |
|
|
 Скачать 1.77 Mb.
Скачать 1.77 Mb.