БИЛЕТ№12.
1)Момент импульса, момент силы. Уравнение моментов. Момент Инерции силы.
2)Постулаты специальной теории относительности. Следствие из преобразования Лоренса.
3)Задача на тему энергия колебательных движений.
Ответы:
1) Векторное произведение радиуса-вектора материальной точки на ее импульс: называют моментом импульса , этой точки относительно точки О (рис.5.4)
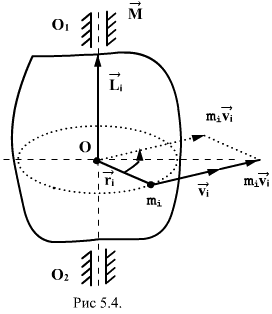
. Вектор иногда называют также моментом количества движения материальной точки. Он направлен вдоль оси вращения перпендикулярно плоскости, проведенной через векторы и и образует с ними правую тройку векторов (при наблюдении из вершины вектора видно, что вращение по кратчайшему расстоянию от к происходит против часовой стрелки).
Векторную сумму моментов импульсов всех материальных точек системы называют моментом импульса (количества движения) системы относительно точки О:
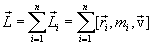
Векторы и взаимно перпендикулярны и лежат в плоскости перпендикулярной оси вращения тела. Поэтому 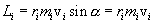 .С учетом связи линейных и угловых величин .С учетом связи линейных и угловых величин
и направлен вдоль оси вращения тела в ту же сторону, что и вектор .
Таким образом.
Момент импульса тела относительно оси вращения
т.е.
Следовательно, момент импульса тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость вращения тела вокруг этой оси.
Момент силы — это мера вращающего действия силы на тело; он определяется произведением модуля силы на ее плечо :
Момент силы считают положительным, когда сила вызывает поворот тела против часовой стрелки, и отрицательным при повороте тела по часовой стрелке (со стороны наблюдателя).
Момент силы — величина векторная: сила проявляет свое вращающее действие, когда она приложена на ее плече (рис. 8, а). Иначе! говоря, линия действия силы не должна проходить через ось вращения. Если сила лежит не в плоскости, перпендикулярной к оси, находят составляющую силы, лежащую в этой плоскости (рис. 8, б); она и вызывает момент силы относительно оси. Остальные составляющие на него не влияют. Понятно, что сила, совпадающая с осью или параллельная ей, также не имеет плеча относительно оси, а следовательно, нет и ее момента.
Тяга каждой мышцы образует момент силы относительно оси соответствующего сустава. Силы, извне приложенные к телу во время движения, обычно не проходят через его центр масс, так что возникают моменты сил относительно ЦМ. Силу, не проходящую через точку (например, через ЦМ), в твердом теле можно привести к этой точке.
2)Постулаты Специальной Теории Относительности (СТО)
Классическая механика Ньютона прекрасно описывает движение макротел, движущихся с малыми скоростями (υ << c). В нерелятивистской физике принималось как очевидный факт существование единого мирового времени t, одинакового во всех системах отсчета. В основе классической механики лежит механический принцип относительности(или принцип относительности Галилея): законы динамики одинаковы во всех инерциальных системах отсчета.Этот принцип означает, что законы динамики инвариантны (то есть неизменны) относительно преобразований Галилея, которые позволяют вычислить координаты движущегося тела в одной инерциальной системе (K
Из преобразований Галилея следует классический закон преобразования скоростейпри переходе от одной системы отсчета к другой.
Принцип относительности: все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. Это означает, что во всех инерциальных системах физические законы (не только механические) имеют одинаковую форму. Таким образом, принцип относительности классической механики обобщается на все процессы природы, в том числе и на электромагнитные. Этот обобщенный принцип называют принципом относительности Эйнштейна.
Принцип постоянства скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Скорость света в СТО занимает особое положение. Это предельная скорость передачи взаимодействий и сигналов из одной точки пространства в другую. Следствия из преобразований Лоренца
1. Если в одной системе отсчета некоторые события происходят в точках x1 и x2 в один и тот же момент вр емени t, то в другой системе отсчета эти события происходят в точкахx'1 и x'2 в разные моменты времени t'1 и t'2:
Понятие одновременности оказывается зависящим от выбора системы отсчета.
2. Если в одной системе отсчета между двумя событиями, происходящими в одной и той же точке, проходит время t, то в другой системе отсче та между этими же событиями проходит время
Это соотношение выражает релятивистский эффект замедления времени в движущихся объектах.
3. Если в одной системе отсчета покоящаяся линейка имеет длину l, то в системе отсчета, в которой линейка движется со скоростью u вдоль своей оси, ее длина
Этот эффект называется релятивистским сокращением продольных размеров тела. Поперечные размеры тела не изменяются при переходе в другие инерциа льные системы отсчета.
4. Если в одной системе отсчета тело имеет скорость v = (vx, vy, vz), то его скорос ть v' = (v'x, v'y, v'z) в другой системе отсчета равна
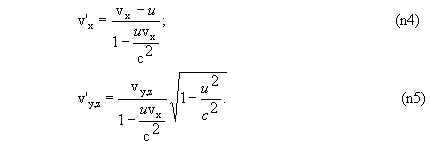
или в трехмерной векторной форме
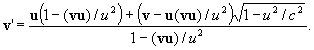
5. Из соотношени (n4), (n5) следует постоянство скорости c в различных системах отсчета. Действительно, если вычислить сумму квадратов левых частей этих равенств при условии
v2=(vx)2+(vy) 2+(vz) 2=c2, (n6)
получим
v'2=(v'x)2+ (v'y)2+(v'z) 2=c2. (n7)
Т. е. скорость c одинакова по величине во всех инерциальных системах отсчета (независимо от направления). Заметим, что направления скоростей v и v' в общем случае различны в разных системах отсчета.
БИЛЕТ №13.
1)Работа, энергия.
2)Инертное свойство и релятивистские частицы, и возможности её ускорения до сверх звуковых скоростей. Кинетическая энергия. Полная энергия. Энергия покоя.
3)Задача по теме Энергия.
Ответы:
1) Работа и Энергия
Термин "работа" в механике имеет два смысла: работа как процесс, при котором сила перемещает тело, действуя под углом, отличном от 90°; работа - физическая величина, равная произведению силы, перемещения и косинуса угла между направлением действия силы и перемещением:
А = Fs cos a.
Работа равна нулю, когда тело движется по инерции (F = 0), когда нет перемещения (s = 0) или когда угол между перемещением и силой равен 90° (cos а = 0). Единицей работы в СИ служит джоуль (Дж).
1 джоуль - это такая работа, которая совершается силой 1 Н при перемещении тела на 1 м по линии действия силы. Для определения быстроты совершения работы вводят величину "мощность".
Мощность равняется отношению совершенной работы ко времени, за которое она выполнена:
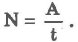
Единицей мощности в СИ служит 1 ватт (Вт). 1 Вт - мощность, при которой совершается работа в 1 Дж за 1 секунду.
Рассмотрим действие на тело некоторой постоянной силы F. На участке пути s будет произведена работа А. В результате у тела изменится скорость:
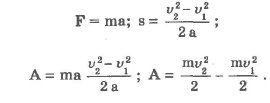
Величину 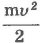 для материальной точки называют кинетической энергией тела. для материальной точки называют кинетической энергией тела.
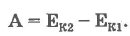
Кинетическая энергия - энергия движения, ею обладают все движущиеся тела. Эта величина является относительной, то есть она изменяется в зависимости от выбранной системы отсчета.
Кроме этого вида механической энергии, существует и другой ее вид - потенциальная энергия. Рассмотрим систему двух взаимодействующих тел. Например, тела, поднятого над Землей, и саму Землю.
Работа силы тяжести при перемещении тела на отрезке |h1 - h2| будет равна:
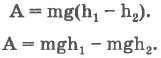
Величину mgh в соответствующей точке, которая расположена на высоте h, называют потенциальной энергией тела, находящегося в поле тяжести.
Из предыдущего уравнения вытекает, что работа не зависит от траектории движения в доле силы тяжести, а определяется лишь изменением высоты.
Потенциальная энергия характеризует и другие взаимодействующие тела. Так, потенциальной энергией обладает сжатая пружина: 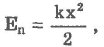
где k - модуль упругости, х - смещение от положения равновесия.
Потенциальная энергия, как и кинетическая, является величиной относительной, поскольку и высота, и смещение зависят от выбора точки отсчета.
2)РЕЛЯТИВИСТСКИЕ ЧАСТИЦЫ. В классической механике основной характеристикой любого тела является масса, определяющая инертные свойства этого тела, т. е. способность получать под действием приложенной к нему внешней силы то или иное ускорение. В новой, вытекающей из специальной теории относительности Эйнштейна так называемой релятивистской механике масса любого тела зависит от его скорости. По мере приближения скорости движения к скорости света масса тела стремится к бесконечности. По этой же причине ни одно тело нельзя разогнать до скорости света. Частицы, масса которых вследствие огромной скорости их движения изменяется в соответствии с приведенным законом, называют релятивистскими.
Энергия - физическая величина, характеризующая состояние тела или системы тел по их движению и взаимодействию. В механике энергия тела или системы тел определяется взаимным положением тел или системы тел и их скоростями.
Кинетическая энергия.
Кинетическая энергия - энергия движущегося тела.(От греческого слова kinema - движение). По определению кинетическая энергия покоящегося в данной системе отсчета тела обращается в ноль.
В СТО масса тела m определяется из уравнения релятивистской динамики:
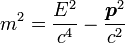
где E — полная энергия свободного тела, p — его импульс, c — скорость света.
Энергия покоя. Энергия покоя E0, или массовая энергия покоя частицы — её энергия, когда она находится в состоянии покоя относительно данной инерционной системы отсчёта; может немедленно перейти в потенциальную (пассивную) и в кинетическую (активную) энергию, что определяется математической формулой эквивалентности массы и энергии следующим образом:
E0 = m0c2,
где m0 - масса покоя частицы, c - скорость света в вакууме.
Можно видеть, что эта формула получается из предыдущей при p = 0, т.е. когда скорость частицы равна нулю.
Релятивистский импульс Четырёх импульс, 4-импульс, релятивистский импульс — 4-вектор энергии-импульса, релятивистское обобщение классического трёхмерного вектора импульса (количества движения) на четырёхмерное пространство-время. Три компоненты классического вектора импульса 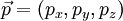 материальной точки при этом становятся тремя пространственными компонентами вектора четырёх импульса. Временной компонентой вектора четырёх импульса является (с точностью до множителя) полная энергия материальной точки. материальной точки при этом становятся тремя пространственными компонентами вектора четырёх импульса. Временной компонентой вектора четырёх импульса является (с точностью до множителя) полная энергия материальной точки.
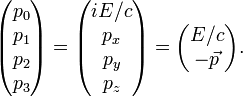
Или другими словами: p = Ev / c
ЭНЕРГИЯ ПОКОЯ тела, энергия E0 свободного тела в системе отсчета, в которой тело покоится: E0=m0c2, где m0 - масса покоя, c - скорость света в вакууме. В энергию покоя входят все виды энергии, кроме кинетической энергии движения тела как целого и потенциальной энергии его взаимодействия с внешним полем. Теоретически извлечь полностью энергию покоя можно лишь при реакциях аннигиляции, при обычных ядерных реакциях извлекаются лишь доли процента, а при химических реакциях
10-8 энергии покоя тела (смотри также Внутренняя энергия).2
БИЛЕТ №14.
1)Потенциальная энергия. Связь между консервативной силой и потенциалом силового поля.
2)Определение колебания, условие возникновения колебания, примеры колебательной системы. Уравнение движение линейного гармонического осциллятора.
3)Задача ….
Ответы:
1) Потенциальная энергия - механическая энергия системы тел, которая определяется характером сил взаимодействия между ними и их взаимным расположением.
Пусть взаимодействие тел друг на друга осуществляется силовыми полями (например, поля упругих сил, поля гравитационных сил), которые характеризуются тем, что работа, совершаемая действующими в системе силами при перемещении тела из первое положения во второе, не зависит от траектории, по которой это перемещение произошло, а зависит только от начального и конечного положений системы. Такие поля называются потенциальными, а силы, действующие в них, - консервативными. В случае, если работа силы зависит от траектории перемещения тела из одного положения в другое, то такая сила называется диссипативной; примером диссипативной силы является сила трения.
Тело, находящееся в потенциальном поле сил, обладает потенциальной энергией P. Работа консервативных сил при элементарном (бесконечно малом) изменении состоянии системы равна приращению потенциальной энергии, взятому с отрицательным знаком, так как работа производится за счет уменьшения потенциальной энергии:
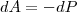 (2) (2)
Работа dA выражается как скалярное произведение силы F на перемещение dr и выражение (2) примет вид
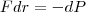 (3) Значит, если известна функция P(r), то из (3) можно найти силу F по модулю и направлению. (3) Значит, если известна функция P(r), то из (3) можно найти силу F по модулю и направлению.
Потенциальная энергия может быть найдена, используя (3) как
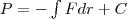 где С - постоянная интегрирования, т. е. потенциальная энергия определяется с точностью до произвольной постоянной. Но это не отражается на физических законах, они спользуют или разность потенциальных энергий в двух различных положениях тела, или производная P по координатам. Поэтому потенциальную энергию тела в каком-то определенном положении считают равной нулю (выбирают удобный для решения прикладных задач нулевой уровень отсчета), а энергию тела в других положениях отсчитывают относительно выбранного нулевого уровня. Для консервативных сил где С - постоянная интегрирования, т. е. потенциальная энергия определяется с точностью до произвольной постоянной. Но это не отражается на физических законах, они спользуют или разность потенциальных энергий в двух различных положениях тела, или производная P по координатам. Поэтому потенциальную энергию тела в каком-то определенном положении считают равной нулю (выбирают удобный для решения прикладных задач нулевой уровень отсчета), а энергию тела в других положениях отсчитывают относительно выбранного нулевого уровня. Для консервативных сил
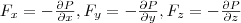
или в векторном виде 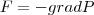 (4) (4)
где 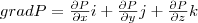 (5) (i, j, k - единичные векторы координатных осей). Вектор, определяемый выражением (5), называется градиентом скаляра P. (5) (i, j, k - единичные векторы координатных осей). Вектор, определяемый выражением (5), называется градиентом скаляра P.
Для него наряду с обозначением grad P применяется также обозначение 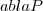 . . 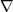 (<набла>) означает символический вектор, называемый оператором Гамильтона или набла-оператором: (<набла>) означает символический вектор, называемый оператором Гамильтона или набла-оператором:
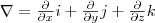 (6) (6)
Конкретный вид функции P зависит от вида силового поля. Например, потенциальная энергия тела массой m, поднятого на высоту h над поверхностью Земли, равна
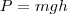 (7) (7)
где высота h отсчитывается от выбранного нулевого уровня, для которого P0=0. Выражение (7) следует из того, что потенциальная энергия тела равна работе силы тяжести при падении данного тела с высоты h на поверхность Земли.
Так как начало отсчета можно выбрать произвольно, то потенциальная энергия может быть величиной меньшей нуля (при этом кинетическая энергия всегда положительна!). Если принять за нуль потенциальную энергию тела, находящегося на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты, глубина которой h', P= -mgh'.
1. Связь между потенциальной энергией и силой. Потенциальная энергия тяготения и упругих деформаций.
Пространство, в котором действуют консервативные силы, называется потенциальным полем. Каждой точке потенциального поля соответствует некоторое значение силы F, действующей на тело, и некоторое значение потенциальной энергии U. Значит, между силой F и U должна быть связь , с другой стороны, dA = –dU, следовательно Fdr=-dU, отсюда: 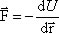
Проекции вектора силы на оси координат: 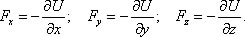
Вектор силы можно записать через проекции: 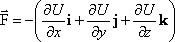 , F = –grad U, где . , F = –grad U, где .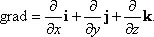
Градиент – это вектор, показывающий направление наибыстрейшего изменения функции. Следовательно, вектор направлен в сторону наибыстрейшего уменьшения U.
|
 Скачать 1.58 Mb.
Скачать 1.58 Mb.