Ответы. Задача по теме Работа. Мощность. Ответы

• Название: Задача по теме Работа. Мощность. Ответы
• Анкор: Ответы.doc
• Дата: 14.05.2017
• Размер: 1.58 Mb.
• Имя файла: Ответы.doc
• Тип: Задача; #7583
• страница: 6 из 9

БИЛЕТ№21

1) Произвольно движущаяся система отсчета. Теорема Кориолиса, Сила Кориолиса.

2)Волновое движение. Частота, Длина волны, поляризация, скорость.

3)Задача на определение положение центра масс.
Ответы:

1)

2) Волны - это изменение состояния среды (возмущения), распространяющиеся в этой среде и несущие с собой энергию и импульс без переноса вещества. Наиболее часто встречающиеся виды волн — упругие (звук) и электромагнитные (свет, радиоволны и другие).

Примером волнового движения может быть возмущение воды от падающих капель, которое распространяется в виде расширяющихся концентрических кругов.

Волновое уравнение: A = A0 cos(ωt + kx)

Волновое уравнение описывает распространение гармонических колебаний в пространстве. Характерными параметрами, описывающими гармоническую волну являются: A0 - амплитуда колебаний; ω - круговая частота (рад/с); период колебаний T (с), который связан с круговой частотой соотношением: T = 2π/ω; частота колебаний γ (Гц = 1/с) выражается через период: γ = 1/T; волновое число k = ω/v (где v- скорость распространения волны, измеряется в м/с); λ - длина (м) волны (λ = vT). Скорость распространения каждого вида волн зависит от свойств среды, в которой они распространяются. Если колебания совершаются поперек по отношению к направлению распространения волн, они называются поперечными, если вдоль - продольными.

Виды волн: поперечные, продольные, поверхностные.

Продольные волны могут возникать, как в твердых телах, так и в жидкостях и газах.

Поперечные волны могут возникать в твердых телах.

Частота и длина волны

Электромагнитная волна характеризуется одним главным параметром — числом гребней, которые за секунду проходят мимо наблюдателя (или поступают в детектор). Эту величину называют частотой излучения ν. Поскольку для всех электромагнитных волн скорость в вакууме (с) одинакова, по частоте легко определить длину волны λ:

λ = с/ν.

Мы просто делим путь, пройденный светом за секунду, на число колебаний за то же время и получаем длину одного колебания. Длина волны — очень важный параметр, поскольку она определяет пограничный масштаб: на расстояниях заметно больше длины волны излучение подчиняется законам геометрической оптики, его можно описывать как распространение лучей. На меньших расстояниях совершенно необходимо учитывать волновую природу света, его способность обтекать препятствия, невозможность точно локализовать положение луча и т. п.

Из этих соображений, в частности, следует, что невозможно получить изображение объектов, если их размер порядка или меньше длины волны излучения, на которой ведется наблюдение. Это, в частности, ставит предел возможностям микроскопов. В видимом свете невозможно рассмотреть объекты размером менее полмикрона; соответственно, увеличение больше чем 1-2 тысячи раз для оптического микроскопа лишено смысла.

ПОЛЯРИЗАЦИЯ ВОЛН

- характеристика волн, определяющая пространственную направленность векторных волновых полей. Исторически это понятие было введено в оптике ещё во времена "довекторных описаний" и первоначально основывалось на свойствах поперечной анизотропии волновых пучков (см. Поляризация света). Оно распространено на все без исключения типы физ. волновых возмущений (см. Волны), но осн. терминология по-прежнему осталась связанной с эл.-магн. (в частности, оптическими) полями.

Различают продольно и поперечно поляризованные волны в зависимости от ориентации вектора поля относительно волнового вектора (k). В электродинамике примером продольных волн служат плоские однородные плазменные волны (см. Ленгмюровские волны); к поперечным волнам в первую очередь относятся плоские однородные эл.-магн. волны в вакууме или в однородных изотропных средах. Поскольку в последних электрич. ( Е) и магн. (Н) векторы перпендикулярны волновому вектору (k), то их часто наз. волнами типа ТЕМ илиТЕН (см. Волновод). Причём, если векторы поля ( Е, Н) лежат в фиксиров. плоскостях ( Е, k) и ( Н,k), т. е. имеют фиксиров. направления в пространстве, используется термин "волны линейной поляризации". Суперпозиция двух линейно поляризованных волн, распространяющихся в одном направлении (k) и имеющих одинаковую частоту но отличающихся направленностью векторных полей, даёт в общем случае волну эллиптической поляризации. В ней концы векторов E. и H описывают в плоскости, перпендикулярной k, эллиптич. траектории, ориентированные по правому или по левому винту в направлении k в зависимости от знака и величины разности фаз  между исходными линейно поляризованными составляющими. Соответственно, такая волна наз. право- или левополяризованной, что не совпадает с терминологией, принятой в оптике, где отсчёт направления вращения вектора поля ведётся в направлении (-k), т. е. в направлении на источник. В частном случае вырождения эллипсов в окружности волны становятся циркуляр-но поляризованными. Иногда именно волны с циркулярной (круговой) поляризацией выбирают в качестве нормальных мод среды. Линейно, эллиптически и цир-кулярно поляризованные волны являются полностью поляризованными волнами. Неполяризов. волны имеют в отличие от них некоррелированное во времени случайное направление векторов полей ( Е и Н) (в оптике - естественный свет). Когда в волновом поле наряду со случайной присутствует ещё и поляризов. составляющая, то говорят о частично поляризованных волнах, количественно характеризуемых степенью поляризации, равной отношению средней по времени интенсивности поляризованной части излучения к полному её значению (см. Когерентность).

Весьма сложными поляризац. свойствами обладают пространственно неоднородные волны, к-рые в принципе можно рассматривать как суперпозицию однородных плоских волн (см.Волновод). При этом характер поляризации векторов Е и Н часто оказывается различным. Так, если в бегущих вдоль оси x волнах типа ТМ поле Н. ориентировано в поперечной к kплоскости  а поле Е образует эллипс поляризации в плоскости ( Е, k), то в волнах типа ТЕ данное свойство видоизменяется Для чисто стоячих волн приходится всегда указывать, относительно какого направления ориентированы эллипсы поляризации.

В неоднородных средах, как правило, описать поляризацию волновых полей очень трудно. Обычно ограничиваются рассмотрением лишь случая кусочно-однородных сред, в частности задачи о падении плоской волны на резкую границу раздела двух однородных изотропных сред (см. Френеля формулы).

В анизотропных средах волны разной поляризации имеют разл. скорости распространения и разл. коэф. затухания. Поэтому при падении волны на границу раздела с анизотропной средой могут возникать сразу неск. преломлённых волн, распространяющихся под углами, отличными от устанавливаемых Снелля законами. Такие свойства анизотропных сред лежат в основе многих поляризационных приборов (разл. поляризаторов, деполяризаторов, поляризац. анализаторов, компенсаторов и т. п.)
БИЛЕТ №22

1)Диаграмма растяжений. Закон Гука.

2)Интерференция, Дифракция механических волн, с примерами.

3)Задача по теме кинематика поступательного движения.

ОТВЕТЫ:

1) Диаграмма растяжения. Определения предела текучести и предела прочности

На рисунке 1 приведена кривая зависимости напряжения от деформации.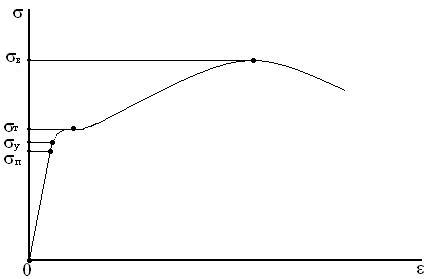




Рисунок 1

Описание характерных точек диаграммы.

σп - Наибольшее напряжение, до которого материал следует закону Гука, называется пределом пропорциональности. Предел пропорциональности зависит от условно принятой степени приближения, с которой начальный участок диаграммы можно рассматривать как прямую.

Упругие свойства материала сохраняются до напряжения, называемого пределом упругости σу , т.е это наибольшее напряжение, до которого материал не получает остаточных деформаций.

σт - предел текучести.

Под пределом текучести понимается то напряжение, при котором происходит рост деформации без заметного увеличения нагрузки. В тех случаях, когда на диаграмме отсутствует явно выраженная площадка текучести, за предел текучести условно принимается величина напряжения, при котором остаточная деформация составляет 0,2%.

Отношение максимальной силы, которую способен выдержать образец, к его начальной площади поперечного сечения носит названиепредела прочности или временного сопротивления. Предел прочности также является условной величиной.

Единица измерения предела текучести и предела прочности - паскаль Па. Более удобно предел текучести и предел прочности измерять в мегапаскалях МПа.

Закон Гука раскрывает вязь между напряжением и деформацией упругой среды. Применяется исключительно в отношении малых напряжений и деформаций. В некоторых средах закон Гука не применяется вовсе. Если взять тонкий стержень, который будут растягивать, то закон можно записать в виде формулы:

F=-kΔх F – сила натяжения стержня;
Δх  - удлинение стержня;

k -  коэффициент упругости (жесткость);

k определяется свойствами материала, который подвергается деформации, и размерами материального тела.

 

2) Явление интерференции возникает при наложении когерент­ных волн.

Когерентные волны - это волны, имеющие одинаковые частоты, постоянную раз­ность фаз, а колебания происходят в одной плоскости.

Результат суперпозиции волн зависит от того, в каких фазах накладываются друг на друга колебания.

Если волны от источников А и Б придут в точку С в одинаковых фазах, то произойдет усиление колебаний; если же — в про­тивоположных фазах, то наблюдается ослабление колебаний.

Постоянное во времени явление взаимного усиления и ослаб­ления колебаний в разных точках среды в результате наложения когерентных волн называется интерференцией. В результате в пространстве образуется устойчивая картина чередования об­ластей усиленных и ослабленных колебаний.

 Если разность хода волн равна целому числу волн (т. е. четному числу по­луволн), то в точке наложения этих волн образуется интерференционный максимум.

Если разность хода волн равна нечетному числу полуволн, то в точке наложения этих волн образуется интерференционный минимум.

   Если разность хода не определяется данными соотношениями, то наблюдается промежуточный результат: 0<А<2х.

Распределение энергии при интерференции.

Наличие минимума в точке С означает: энергия W сюда не поступает.

Наличие максимума в точке С означает: происходит увеличе­ние за счет перераспределения энергии в пространстве. Так как энергия пропорциональна квадрату амплитуды, ТО при увели­чении амплитуды в 2 раза энергия увеличивается в 4 раза. Это означает, что в точку С поступает энергия в 4 раза боль­ше энергии одного вибратора при условии: энергии вибраторов равны.

Интерференция присуща волнам любой природы (механиче­ским, электромагнитным).

Стоячие волны

Если раскачивать один конец веревки с правильно подобран­ной частотой (другой ее конец закреплен), то к закрепленному концу побежит непрерывная волна, которая затем отразится с потерей полуволны. Интерференция падающей и отраженной волн приведет к возникновению стоячей волны, которая выгля­дит неподвижной.

Устойчивость стоячей волны удовлетворяет следующему условию:  где L—длина веревки; п=1, 2, 3 и т.д.; v—скорость распро­странения волны, которая зависит от натяжения веревки. Стоячие волны возбуждаются в любых телах, способных со­вершать колебания. Точки, где интерференция гасится, называются узлами, а точки, где интерференция усиливается,— пучностями. Помимо поперечных стоячих волн существуют еще и продольные стоячие волны.

Нередко волна встречает на своем пути небольшие (по сравнению с длиной волны) препятствия, которые она способна огибать. Когда размеры препятствий малы, волны, огибая края препятствий, смыкаются за ними. Так, морские волны свободно огибают выступающий из воды камень, если его размеры меньше длины волны или сравнимы с ней. За камнем волны распространяются так, как если бы его не было совсем. Точно так же волна от брошенного в пруд камня огибает торчащий из воды прутик. Только за препятствием большого по сравнению с длиной волны размера (большой камень на рисунке 8.52) образуется «тень»: волны за него не проникают.

Способностью огибать препятствия обладают и звуковые волны. Вы можете слышать сигнал машины за углом дома, когда самой машины не видно. В лесу деревья заслоняют ваших товарищей. Чтобы их не потерять или не потеряться самому, вы начинаете кричать. Звуковые волны в отличие от света свободно огибают стволы деревьев и доносят ваш голос до товарищей. Отклонение от прямолинейного распространения волн, или огибание волнами препятствий — называется дифракцией1. Дифракция присуща любому волновому процессу, так же как и интерференция. При дифракции происходит искривление волновых поверхностей у краев препятствий.

Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней.

Явление дифракции волн на поверхности воды можно наблюдать, если, например, поставить на пути волн экран с узкой щелью, размеры которой меньше длины волны (рис. 8.53). В этом опыте хорошо бывает видно, что за экраном распространяется Kpyroiuui волна, как если бы в отверстии экрана находилось колеблющееся тело — источник волн. Согласно принципу Гюйгенса так и должно быть. Вторичные источники в узкой щели располагаются столь близко друг к другу, что их можно рассматривать как один точечный источник.



Если же размеры щели велики по сравнению с длиной    волны, то  картина распространения волн за экраном совершенно иная (рис. 8.54). 

1 От латинского слова difractus — разломанны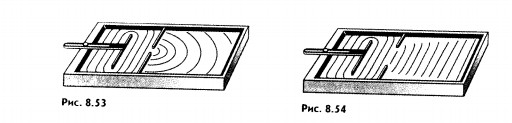
 
Волна проходит сквозь щель, почти не меняя своей формы. По краям можно заметить искривления волновой поверхности, в результате чего волна частично проникает и в пространство за экраном.

Принцип Гюйгенса позволяет понять, почему происходит дифракция. Вторичные волны, испускаемые участками среды, проникают за края препятствия, расположенного на пути распространения волны.

БИЛЕТ №23.

1)Задача кинематики. Кинематические уравнение движения (рассмотреть все виды движения).

2) Волновые пакеты. Фазовая и волновая скорость.

3) Задача по теме динамика.

Ответы:

Основная задача кинематики — это получение зависимостей от времени скорости v = v(t) и координат (или радиуса-вектора) r = r(t)материальной точки из известной зависимости от времени ее ускорения a = a(t) и известных начальных усло­вий v0 и r0. 

Существует и обратная задача: по известному закону движения r = r(t) находят скорость и ускоре­ние материальной точки. Решение обеих задач в общем виде возможно с помощью дифференциального и ин­тегрального исчисления.

Для некоторых простых частных случаев движения задача может быть решена с применением методов элементарной математики. Для прос­тоты рассмотрим движение тел в плоскости XOY.

А) Равномерное прямолинейное движение материальной точки; a = 0, v = const. Начальные условия: х0, у0.
Б) Равноускоренное прямолиней­ное движение материальной точки: a = const. Начальные условия: х0, у0; v0x, v0y.
В) Движение тела по дуге окруж­ности с постоянной по модулю скоростью было рассмотрено выше. Однако возможен другой подход.

Формулу центростремительного ускорения можно получить, рассмат­ривая проекции на координатные оси ОХ и ОУ радиуса вектора r точки, движущейся по окружности с задан­ной угловой скоростью, и вектора скорости v этой точки.
Г) Гармоническое колебательное движение. Важным случаем механи­ческого движения являются колеба­ния, при которых параметры движе­ния точки (координаты, скорость, ус­корение) повторяются через опреде­ленные промежутки времени. Опыт показывает, что если точка движется по окружности с постоянной по моду­лю скоростью, то проекции радиуса-вектора этой точки совершают коле­бания. Если зависимость координаты от времени выражается через функ­цию синус или косинус, то такие колебания называются гармоничес­кими

Анализ выражения (4) пока­зывает, что проекции радиуса-векто­ра точки совершают гармонические колебания. При этом по гармони­ческому закону изменяются также проекции скорости и ускоре­ния.

При движении материальной точки М ее координаты  и радиус-вектор  изменяются с течением времени t.

Поэтому для задания закона движения м.т. необходимо указать либо вид функциональной зависимости всех трех ее координат от времени:

либо зависимость от времени радиус-вектора этой точки

Три скалярных уравнения (1.2) или эквивалентное им одно векторное уравнение (1.3) называются кинематическими уравнениями движения материальной точки.

2) Волновые пакеты. Фазовая и волновая скорость.

ВОЛНОВОЙ ПАКЕТ - волновое образование из колебаний произвольной природы, представляющее собой суперпозицию (наложение) плоских монохроматич. волн с близкими значениями частот  и волновых векторов (k). B случае одного пространственного измерения (х)и скалярного комплексного волнового поля В. п.  можно представить в виде интеграла Фурье:



где g (k)заметно отлично от нуля лишь для значений k, лежащих внутри интервала вблизи нек-рого k=k0. В отличие от плоской монохроматич. волны, существующей во всем пространстве, В. п. занимает конечную часть пространства, т. к. из (1) следует:



Разброс  по координатам ф-ции  (ширина пакета) скоррелирован с разбросом Dk ф-ции g(k)по волновым числам k:



Под разбросом (шириной) величины  понимается среднеквадратичное отклонение . Эволюция В. п. (1) предопределена, если известны g (k)и закон дисперсии волн-связь  и k:



Если эта связь линейна, 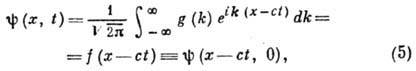 , где с=const (как в случае световых волн в пустоте), то



т. е. В. п. распространяется со скоростью с без изменения своей формы.

В общем случае произвольной связи  и k зависимость  от х и t имеет более сложный вид, и характер распространения В. п. может быть описан следующим усредненным (интегральным) соотношением:



описывающим равномерное движение центра тяжести В. п. с групповой скоростью , и равенством



характеризующим расширение со временем ("расплывание") В. п., где  - среднеквадратичный разброс величины 

В квантовой механике для волны, де Бройля частицы (где р, т - импульс и масса частицы), т. е. совпадает со ср. значением классич. скорости частицы, а , где  - среднеквадратичный разброс по импульсам в В. п. Соотношения (6), (7) и (4) сыграли важную роль в создании осн. квантовых представлений. Тот факт, что центр масс локализованного в пространстве В. п., составленного из волн де Бройля, перемещается со скоростью классич. частицы, явился иллюстрацией предельного перехода квантовомеханич. законов движения к законам движения классич. частицы по классич. траектории. Аналогично факт расплывания В. п. со временем способствовал принятию статистич. интерпретации квантовой механики (поскольку из него следовало, что квадрат модуля волновой функциинельзя рассматривать как плотность частицы). Учитывая, что в квантовой теории  , из (3) непосредственно получается неопределенностей соотношение для координаты и импульса:

Для движения частицы во внеш. поле в случае, когда спектр её энергии дискретен, также может быть рассмотрен В. п., представляющий собой суперпозицию состояний с разл. значениями энергии. Центр масс такого В. п. тоже движется по классяч. траектории, при этом для нек-рых потенциалов поля (типа потенциала поля осциллятора) существуют нерасплывающиеся В. п. (см. Когерентное состояние).

При использовании соотношений (6), (7) для распространения света в среде следует иметь в виду, что они получены в предположении вещественности  , т. е. в пренебрежении эффектами диссипации. Эти соотношения могут оказаться неправильными при их формальном использовании в случае В. п. с частотами, лежащими вблизи области т. н. аномальной дисперсии данной среды, где диссипац. эффектами пренебрегать нельзя. В этой области частот понятие групповой скорости теряет смысл, поскольку при движении В. п. будет происходить его сильное экспоненциальное затухание, как это следует из выражения (1).