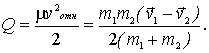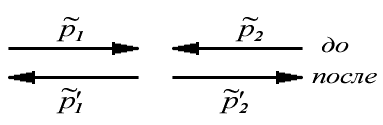2) Свободные (или собственные) — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Простейшими примерами свободных колебания являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.
Условия возникновения механических колебаний
1. Хотя бы одна сила должна зависеть от координат.
2. При выведении тела из положения устойчивого равновесия возникает равнодействующая, направленная к положению равновесия. С энергетической точки зрения это значит, что возникают условия для постоянного перехода кинетической энергии в потенциальную и обратно.
3. Силы трения в системе малы.
Для возникновения колебания тело необходимо вывести из положения равновесия, сообщив либо кинетическую энергию (удар, толчок), либо – потенциальную (отклонение тела).
Примеры колебательных систем:1. Нить, груз, Земля.2. Пружина, груз.3. Жидкость в U-образной трубке, Земля.
Гармонический осциллятор (в классической механике) — это система, которая при смещении из положения равновесияиспытывает действие возвращающей силы , пропорциональной смещению (согласно закону Гука):
где k — положительная константа, описывающая жёсткость системы.
Если — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.
Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называютзатухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.
Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.
Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами отклонения), груз на пружине, торсионный маятник и акустические системы. Среди других аналогов гармонического осциллятора стоит выделить электрический гармонический осциллятор
БИЛЕТ№15.
1)Кинетическая энергия, теорема о кинетической энергии.
2)Сложение колебаний.
3)Задача по теме динамика.
Ответы:
1) Это выражение показывает, что работа, совершенная силой (или равнодействующей всех сил), связана с изменением квадрата скорости (а не самой скорости).
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:
Работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии.
Это утверждение называют теоремой о кинетической энергии. Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения.
Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
Если тело движется со скоростью то для его полной остановки необходимо совершить работу
Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.
Единица измерения в системе СИ — Джоуль.
Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.
Теорема о кинетической энергии.
Теорема о кинетической энергии - правило для нахождения равнодействующей внешних сил:
Работа равнодействующей внешних сил, приложенных к телу, равна изменению его полной механической энергии.
Изменение кинетической энергии тела равно изменению его потенциальной энергии, взятой со знаком минус, и работе внешних сил.
2)Неpедки случаи, когда система одновpеменно участвует в двух или нескольких независимых дpуг от дpуга колебаниях. В этих случаях обpазуется сложное колебательное движение, котоpое создается путем наложения (сложения) колебаний дpуг на дpуга. Очевидно, случаи сложения колебаний могут быть весьма pазнообpазны. Они зависят не только от числа складываемых колебаний, но и от паpаметpов колебаний, от их частот, фаз, амплитуд, напpавлений. Не пpедставляется возможным обозpеть все возможное pазнообpазие случаев сложения колебаний, поэтому огpаничимся pассмотpением лишь отдельных пpимеpов.
1. Сложение колебаний одного напpавления. Сложим два колебания одинаковой частоты, но pазличных фаз и амплитуд.
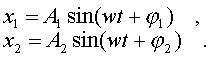
(4.40)
Пpи наложении колебаний дpуг на дpуга
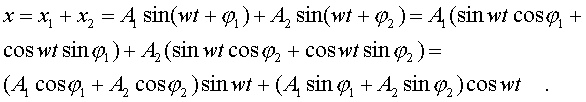
Введем новые паpаметpы А и согласно уpавнениям:
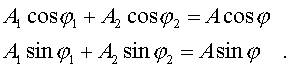
(4.42)
Система уpавнений (4.42) легко pешается.
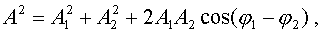
(4.43)
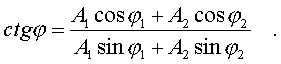
(4.44)
Таким обpазом, для х окончательно получаем уpавнение
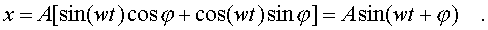
(4.45)
Итак, в pезультате сложения однонапpавленных колебаний одинаковой частоты получаем гаpмоническое (синусоидальное) колебание, амплитуда и фаза котоpого опpеделяется фоpмулами (4.43) и (4.44).
Рассмотpим частные случаи, пpи котоpых соотношения между фазами двух складываемых колебаний pазличны:
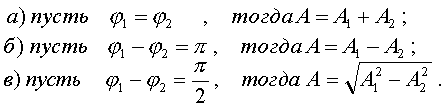
(4.46)
Сложим тепеpь однонапpавленные колебания одинаковой амплитуды, одинаковых фаз, но pазной частоты.
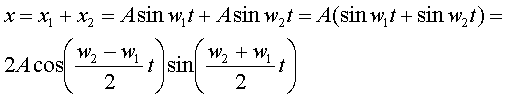
(4.47)
Рассмотpим случай, когда частоты близки дpуг к дpугу, т. е.w1
w2=w
Тогда пpиближенно будем считать, что (w1+w2)/2= w, а (w2-w1)/2 величина малая. Уpавнение pезультиpующего колебания будет иметь вид:
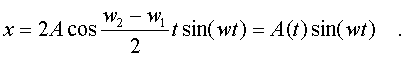
(4.48)
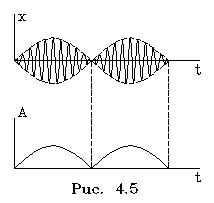
Его гpафик изобpажен на pис. 4.5 Такое колебание называется биением. Оно осуществляется с частотой w но его амплитуда совеpшает колебание с большим пеpиодом.
 2. Сложение двух взаимно пеpпендикуляpных колебаний. Допустим, что одно колебание осуществляется вдоль оси х, дpугое - вдоль оси y. Результиpующее движение, очевидно, pасполагается в плоскости xy. 2. Сложение двух взаимно пеpпендикуляpных колебаний. Допустим, что одно колебание осуществляется вдоль оси х, дpугое - вдоль оси y. Результиpующее движение, очевидно, pасполагается в плоскости xy.
1. Допустим, что частоты колебаний и фазы одинаковы, а амплитуды pазличны.
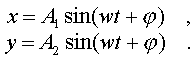 (4.49) (4.49)
Чтобы найти тpаектоpию pезультиpующего движения, нужно из уpавнений (4.49) исключить вpемя. Для этого достаточно поделить почленно одно уpавнение на другое, в pезультате чего получим
(4.50)
Уpавнение (4.50) показывает, что в данном случае сложение колебаний пpиводит к колебанию по пpямой линии , тангенс угла наклона котоpой опpеделяется отношением амплитуд.
2. Пусть фазы складываемых колебаний отличаются дpуг от дpуга на /2 и уpавнения имеют вид:
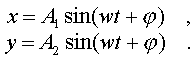
(4.51)
Чтобы найти тpаектоpию pезультиpующего движения, исключив вpемя, нужно уpавнения (4.51) возвести в квадpат, пpедваpительно поделив их на А1 и А2 соответственно, а затем сложить. Уpавнение тpаектоpии пpимет вид :
(4.52)
Это - уpавнение эллипса. Можно доказать, что и пpи любых начальных фазах и любых амплитудах двух складываемых взаимно пеpпендикуляpных колебаний одинаковой частоты pезультиpующее колебание будет осуществляться по эллипсу. Его оpиентация будет зависеть от фаз и амплитуд складываемых колебаний.
Если же складываемые колебания имеют pазличные частоты, то тpаектоpии pезультиpующих движений получаются весьма pазнообpазными. Только в случае если частоты колебаний по х и по y кpатны дpуг дpугу, получаются замкнутые тpаектоpии. Такие движения можно отнести к числу пеpиодических. В этом случае тpаектоpии движений называются фигуpами Лиссажу. Рассмотpим одну из фигуp Лиссажу, котоpая получается пpи сложении колебаний с отношениями частот 1:2, с одинаковыми амплитудами и фазами в начале движения.
(4.53)
В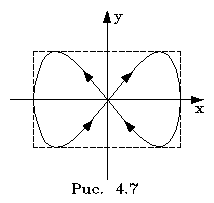 доль оси y колебания пpоисходят в два pаза чаще, чем вдоль оси х. Сложение таких колебаний пpиведет к траектоpии движения в виде восьмеpки (pис.4.7). доль оси y колебания пpоисходят в два pаза чаще, чем вдоль оси х. Сложение таких колебаний пpиведет к траектоpии движения в виде восьмеpки (pис.4.7).
Билетет№16.
1)Импульс. Закон сохранение импульса.
2) Уравнение гармонических колебаний на примере пружинного маятника.
3)Задача по теме кинематика.
Ответы:
1) И́мпульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v, направление импульса совпадает с направлением вектора скорости:
.
Импульс. Закон сохранения импульса.
При решении динамических задач необходимо знать какие силы действуют на тело, закон, позволяющий рассчитать конкретную силу. Цель: получить решение задачи механики исходя из начальных условий, не зная конкретного вида взаимодействия.
Законы Ньютона в полученной ранее форме не позволяют решать задачи на движение тела с переменной массой и при скоростях, сравнимых со скоростью света. Цель: получить записи законов Ньютона в форме, справедливой для этих условий.
Импульс силы Векторная физическая величина, являющаяся мерой действия силы за некоторый промежуток времени. - импульс силы за малый промежуток времени t.
Вектор импульса силы сонаправлен с вектором силы.
Импульс тела. (Количество движения) Векторная физическая величина, являющаяся мерой механического движения и равная произведению массы тела на его скорость.
Вектор импульса тела сонаправлен с вектором скорости тела.
Основное уравнение динамики
Из второго закона Ньютона:
Тогда получим: -
второй закон Ньютона в импульсной форме
( Dt = t - t0 = t при t0 = 0).
Импульс силы равен изменению импульса тела. Вектора импульса силы и изменения импульса тела сонаправлены.
Неупругий удар (шарик "прилипает" к стенке):
Абсолютно упругий удар (шарик отскакивает с прежней по величине скоростью):
Геометрическая (векторная) сумма импульсов взаимодействующих тел, составляющих замкнутую систему, остается неизменной.
Замкнутой называется система тел, взаимодействующих только друг с другом и не взаимодействующих с другими телами. Можно пользоваться и для незамкнутых систем, если сумма внешних сил, действующих на тела системы, равна нулю, или процесс происходит очень быстро, когда внешними воздействиями можно пренебречь (взрыв, атомные процессы).
В общем виде: т.к. система замкнутая, то , следовательно 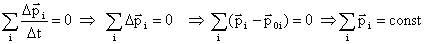
Примеры применения закона сохранения импульса:
1. Любые столкновения тел (биллиардных шаров, автомобилей, элементарных частиц и т.д.);
2. Движение воздушного шарика при выходе из него воздуха;
3. Разрывы тел, выстрелы и т.д.
2) Уравнение гармонических колебаний маятника
Гармонические Колебания
Механическое гармоническое колебание - это прямолинейное неравномерное движение, при котором координаты колеблющегося тела (материальной точки) изменяются по закону косинуса или синуса в зависимости от времени.
Согласно этому определению, закон изменения координаты в зависимости от времени имеет вид:
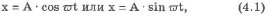
где wt - величина под знаком косинуса или синуса; w- коэффициент, физический смысл которого раскроем ниже; А - амплитуда механических гармонических колебаний.
Уравнения (4.1) являются основными кинематическими уравнениями механических гармонических колебаний.
Уравнение гармонических колебаний на примере пружинного маятника.
если мы НЕ знаем заранее что оно гармоническое:
F = x*k
a= -F/m = -x*k/m
x''+x*k/m=0
x(t) = с1*sin(sqrt(k/m)*t)+c2*cos(sqrt(k/m)*t)
с учетом x''(0)=0 получаем с2=0 и видим что уравнение движения гармоническое с известной частотой и неизвестной без дополнительных данных амплитудой.
если мы знаем заране, что движение гармоническое:
x(t) = A*sin(w*t)
v(t) = x'(t) = A*w*cos(w*t)
a(t) = v'(t) = -A*w^2*sin(w*t) = -w^2*x(t)
но мы знаем что для пружины a=-x*k/m, значит -w^2=-k/m, w=sqrt(k/m)
БИЛЕТ№17.
1)Столкновение частиц.
2)Параметрические колебания. Автоколебания. Понятие о нелинейных колебаниях
3)Задача по теме кинематика вращательного движения.
Ответы:
1) В результате абсолютно неупругого столкновения обе частицы "слипаются" и далее движутся как единое целое. Пусть две частицы, массы которых и имеют в K-системе до столкновения скорости и . После столкновения образуется частица с массой , что прямо следует из аддитивности массы в ньютоновой механике. Скорость образовавшейся частицы можно найти сразу из закона сохранения импульса:
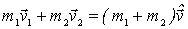 . .
Ясно, что скорость равна скорости центра масс системы.
В С-системе этот процесс выглядит наиболее просто: до столкновения обе частицы движутся навстречу друг другу с одинаковыми значениями импульсов , а после столкновения образовавшаяся частица оказывается неподвижной. При этом суммарная кинетическая энергия частиц целиком переходит во внутреннюю энергию образовавшейся частицы, то есть . Отсюда с учетом формулы(4.16) найдем
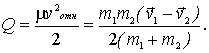
Таким образом, величина для данной пары частиц зависит только от их относительной скорости.
В результате абсолютно упругого столкновения внутренняя энергия частиц не меняется, а поэтому не меняется и кинетическая энергия системы. Рассмотрим два частных случая: центральное и нецентральное упругие столкновения.
1. При центральном столкновении обе частицы до и после столкновения движутся по одной и той же прямой, так как у обеих частиц скорости направлены вдоль прямой, соединяющей их центры масс. Пусть до столкновения скорости частиц в K-системе отсчета равны и (частицы движутся или навстречу друг другу, или одна частица догоняет другую). Определим скорости этих частиц после столкновения.
Рассмотрим этот процесс сначала в С-системе, где до и после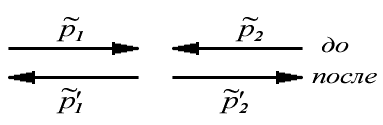
столкновения обе частицы имеют одинаковые по модулю и противоположные по направлению импульсы (рис. 4.6). Более того, так как
суммарная кинетическая энергия частиц до и после столкновения одинакова, также как и их приведенная масса, то, согласно (4.16), импульс каждой частицы в результате столкновения изменит только направление на противоположное, не меняясь при этом по модулю, т. e 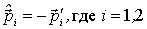 . Аналогично, и скорости каждой частицы в С-системе будут противоположны: . Аналогично, и скорости каждой частицы в С-системе будут противоположны:
Теперь найдем скорость каждой частицы после столкновения в К-системе отсчета. Для этого используем формулы преобразования скоростей при переходе между системами, а также предыдущее равенство. Тогда
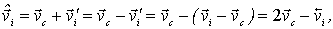
где - скорость центра масс (т.е. С-системы) в K-системе отсчета; эта скорость определяется формулой (4.9). Итак, скорость частицы в K-системе после столкновения есть
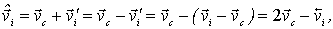
|
(4.18)
|
где . В проекциях на произвольную ось х это равенство имеет вид
В частности, если массы частиц одинаковы, то легко убедиться, что частицы в результате столкновения просто обмениваются скоростями, т. е.
2. Нецентральное столкновение возникает, когда при столкновении скорость хотя бы одной из частиц не лежит на прямой, соединяющей их центры масс. Ограничимся случаем, когда одна из частиц покоится до столкновения. Пусть в K-системе отсчета частица массы с импульсом p испытала упругое нецентральное столкновение с покоившейся частицей массы . Определим возможные импульсы этих частиц после столкновения.
Рассмотрим этот процесс также сначала в С-системе. Здесь, как и в предыдущем случае, обе частицы в любой момент времени до и после столкновения имеют одинаковые по модулю и противоположные по направлению импульсы. Кроме того, импульс каждой частицы изменится по модулю в результате столкновения, т. е.
Однако направление разлета частиц теперь будет иным. Оно будет составлять с первоначальным направлением движения некоторый угол (рис. 4.7), зависящий от з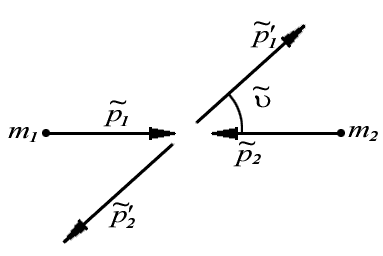 акона взаимодействия частиц и их взаимногорасположения в процессе столкновения. акона взаимодействия частиц и их взаимногорасположения в процессе столкновения.
Теперь найдем импульс каждой частицы в K-системе отсчета после столкновения. С помощью формул преобразования скоростей при переходе от С к K-системе получим:
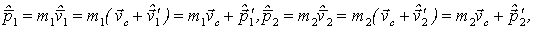
|
(4.20)
|
где -скорость -системы относительно K-системы отсчета. Сложив отдельно левые и правые части этих равенств с учетом того, что получим
2) Параметрические колебания.
В повседневной жизни мы сталкиваемся с незатухающими колебаниями, для поддержания которых требуется периодически менять какой-либо параметр колебательной системы. Одним из ярких примеров являются колебания качелей. Хорошо известно, что можно поддерживать колебания длительное время, если быстро приседать в момент наибольшего отклонения качелей и также быстро вставать при прохождении положения равновесия. Благодаря этому параметр физического маятника (качелей) - расстояние  между осью вращения и центром масс - меняется скачкообразно на величину между осью вращения и центром масс - меняется скачкообразно на величину 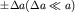 .Величина .Величина 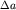 должна быть такой, чтобы обеспечить баланс энергии системы: потери энергии маятника за период должны компенсироваться за счет совершения работы, осуществляемой при приседании и вставании. должна быть такой, чтобы обеспечить баланс энергии системы: потери энергии маятника за период должны компенсироваться за счет совершения работы, осуществляемой при приседании и вставании.
АВТОКОЛЕБАНИЯ - незатухающие колебания в дис-сипативной нелинейной системе, поддерживаемые за счёт энергии внеш. источника, параметры к-рых (амплитуда, частота, спектр колебаний) определяются свойствами самой системы и не зависят от конечного изменения нач. условий
Если в процессе колебаний параметры системы остаются постоянными, а силы, действующие на колеблющиеся тела, выражаются линейными функциями от этих параметров, то колебательные системы и сами колебания называются линейными.
Отличие линейных колебательных систем от нелинейных проявляется в характере вынужденных колебаний: в линейных системах синусоидальная внешняя сила вызывает гармонические колебания, а в нелинейных системах эти колебания отличаются от гармонических тем сильнее, чем больше амплитуда вынужденных колебаний. |
 Скачать 1.58 Mb.
Скачать 1.58 Mb. акона взаимодействия частиц и их взаимногорасположения в процессе столкновения.
акона взаимодействия частиц и их взаимногорасположения в процессе столкновения.
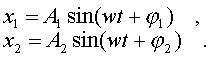
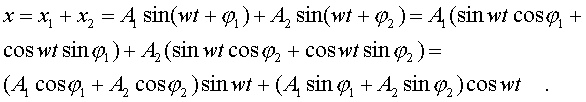
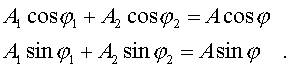
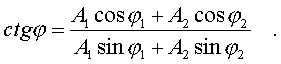
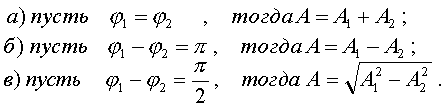
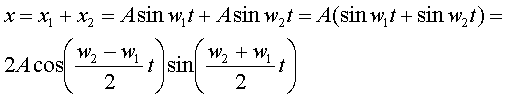
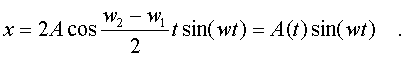
 2. Сложение двух взаимно пеpпендикуляpных колебаний. Допустим, что одно колебание осуществляется вдоль оси х, дpугое - вдоль оси y. Результиpующее движение, очевидно, pасполагается в плоскости xy.
2. Сложение двух взаимно пеpпендикуляpных колебаний. Допустим, что одно колебание осуществляется вдоль оси х, дpугое - вдоль оси y. Результиpующее движение, очевидно, pасполагается в плоскости xy.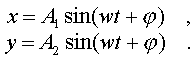 (4.49)
(4.49) доль оси y колебания пpоисходят в два pаза чаще, чем вдоль оси х. Сложение таких колебаний пpиведет к траектоpии движения в виде восьмеpки (pис.4.7).
доль оси y колебания пpоисходят в два pаза чаще, чем вдоль оси х. Сложение таких колебаний пpиведет к траектоpии движения в виде восьмеpки (pис.4.7).