Ответы. Задача по теме Работа. Мощность. Ответы
 Скачать 1.58 Mb.
|
|
БИЛЕТ №24. 1) Основные понятия кинематики (радиус-вектор, координата, траектория, путь, перемещение, скорость, ускорение). 2) Поперечные и продольные волны. Плоские, цилиндрические и сферические волны. 3) Задача по теме «Работа. Мощность». Ответы: Любое физическое явление или процесс в окружающем нас материальном мире представляет собой закономерный ряд изменений, происходящих во времени и пространстве. Механическое движение, то есть изменение положения данного тела (или его частей) относительно других тел, – это простейший вид физического процесса. Механическое движение тел изучается в разделе физики, который называется механикой. Основная задача механики – определить положение тела в любой момент времени. Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина. Пройденный путьl равен длине дуги траектории, пройденной телом за некоторое время t.Путь – скалярная величина. Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути. В случае достаточно малого промежутка времени Δt пройденный телом путь Δl почти совпадает с модулем вектора перемещения При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути.
Для характеристики движения вводится понятие средней скорости: В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt: Мгновенным ускорением (или просто ускорением) тела называют предел отношения малого изменения скорости к малому промежутку времени Δt, в течение которого происходило изменение скорости: Нормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент: Вектор всегда направлен к центру окружности. Из рис. 1.1.5 видно, что модуль полного ускорения равен аким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l, перемещение S, скорость V и ускорение A. Путь l является скалярной величиной. Перемещение S, скорость V и ускорение a – величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д. 2) В физике мы имеем дело с волнами различной природы: механическими, электромагнитными и т.д. Несмотря на отличия, эти волны имеют много общих черт. Волны, рассматриваемый параметр которых (смещение молекул, механическое напряжение, и т.д.) изменяется периодически вдоль оси распространения, называются продольными волнами. Если колебания происходят перпендикулярно оси распространения волны (как у электромагнитных волн, например), то такие волны называются поперечными. Если взаимосвязь между частицами среды осуществляется силами упругости, возникающими вследствие деформации среды при передаче колебаний от одних частиц к другим, то волны называются упругими. К ним относятся звуковые, ультразвуковые, сейсмические и др. волны. На первой анимации изображён процесс распространения продольной упругой волны в решётке, состоящей из шариков, соединённых упругими пружинками. Каждый шарик колеблется по гармоническому закону в продольном направлении, совпадающем с направлением распространения волны. Амплитуда каждого шарика одинакова и равна A, а фаза колебаний линейно растёт с увеличением номера шарика на т.е. x0=Asin(t); x1=Asin(t+); x2=Asin(t+2); x3=Asin(t+3); и т.д. где -частота волны, t - время, - изменение фазы от шарика к шарику В поперечной волне колебания происходят в направлении, перпендикулярном направлению распространения волны. Как и в случае продольных волн амплитуды колебаний всех шариков одинаковы, а фаза линейно изменяется от шарика к шарику y0=Bsin(t); y1=Bsin(t+); y2=Bsin(t+2); y3=Bsin(t+3); и т.д. В общем виде уравнение распространения волны может быть записано в виде: z = Acos(tkxгде z - координата, по которой происходит движение частиц, x - координата оси, вдоль которой распространяется волна, k - волновое число, равное / v, v - скорость распространения волны. Зная частоту волны и скорость её распространения, мы можем найти сдвиг фаз между соседними шариками (частицами): / v)a, где a - расстояние между шариками в решётке. На следующей анимации изображено наложение продольной и поперечной волн равной амплитуды, сдвинутых по фазе на 90 градусов. В результате каждая масса совершает круговые движения. Уравнение движения каждого шарика может быть описано уравнением: x=Acos(t+); y=Asin(t+) У волн, наблюдаемых на поверхности жидкости, так называемых поверхностных волн, взаимосвязь между соседними элементами поверхности жидкости при передаче колебаний осуществляется не силами упругости, а силами поверхностного натяжения и тяжести. Колебания масс в сетке моделируют движение молекул в волне на поверхности жидкости. В случае малой амплитуды волны каждая масса движется по окружности, радиус которой убывает с расстоянием от поверхности. Массы внизу сетки находятся в покое. Волны на поверхности жидкости не являются ни продольными, ни поперечными. Как мы можем видеть на анимации, красный шарик, моделирующий молекулу поверхности жидкости, движется по круговой траектории. Таким образом, волна на поверхности жидкости представляет собой суперпозицию продольного и поперечного движения молекул. БИЛЕТ №25. 1)Основная задача механика. Начальные условия. Обратимость уравнений движения (прямая и обратная задача). 2)Фазовая диаграмма гармонического осциллятора. 3)Задача по теме кинематика поступательного движения. Ответы: 1) Основная задача механики, как неоднократно указывается в учебнике «Физика 8», — определять положение (координаты) движущегося тела в любой момент времени. Это механика обязательно должна «уметь», иначе она не может быть наукой о движении. Законы движения, открытые Ньютоном, и прежде всего второй закон Ньютона (основной закон динамики) как раз и позволяют решать эту задачу. Второй закон Ньютона связывает силу, приложенную к телу, и вызванное силой ускорение. Но ускорение — это быстрота изменения скорости, а скорость, в свою очередь, — быстрота изменения перемещения тела. Поэтому, решив уравнение, выражающее основной закон динамики, мы узнаем о быстроте изменения координат тела, а значит, и о самих координатах в любой момент времени. Для этого кроме силы нужно знать еще начальные условия — начальные координаты и начальную скорость тела. На первый взгляд кажется, что уравнение второго закона Ньютона очень простое и что решается оно тоже просто. Однако надо помнить, что уравнение — векторное. Это значит, что за ним «скрываются» три скалярных уравнения для проекции силы и ускорения на оси координат: 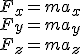 .Эти уравнения в самом деле решаются легко, но только в том случае, когда проекции силы Fx, Fy и Fz постоянны, то есть когда их значения одинаковы при любых значениях координат точки, а значит, и в любой момент времени. Тогда постоянны и значения проекций ускорения ax, ay и az, движение тела, следовательно, равноускоренное, и координаты х, у и z определяются равенствами . Здесь x0, y0 и z0 — начальные координаты, a υ0x, υ0y и υ0z — соответствующие проекции начальной скорости на оси координат. азовые уравнения классической механики полностью обратимы, как известно, относительно инверсии времени, и потому не отражают очевидную необратимость эволюции реальных природных систем. Основная причина такого противоестественного положения состоит на наш взгляд в следующем. В основном уравнении динамики материальной точки dР/dt = F импульс Р = mV и сила F являются векторами, которые по определению не могут отражать необратимость течения времени. Ведь векторы изначально вводились как особая мнимая часть кватернионов, а мнимая часть как обычных комплексных чисел, использующихся, например, при расчете цепей переменного (синусоидального) тока в электротехнике, так и их четырехмерного обобщения в виде собственно кватернионов, описывает только колебательную (в общем случае «вращательную») составляющую совокупного движения! Определяемое же вторым началом термодинамики неизбежное затухание этих колебаний (вращений), с которым и связана искомая необратимость эволюции природных систем, отражается, напротив, действительной частью тех же комплексных чисел или, соответственно, скалярной частью кватернионов, попросту отсутствующей в анализируемом базовом уравнении механики. Отсюда и его неизбежная обратимость относительно инверсии времени, вполне приемлемая, впрочем, для динамики именно материальной точки – ведь последняя представляет собой по сути дела идеализированную механическую систему, по определению лишенную внутреннего движения, с которым и связаны, в конечном счете, необратимые во времени диссипативные процессы. В отношении же динамики реальной механической системы следовало бы ожидать, напротив, что в ее основное уравнение главные динамические величины должны входить уже на сей раз в виде полных кватернионов, что позволило бы отразить все связанные с ней механические процессы, в том числе и необратимые во времени. Но на самом деле названное основное уравнение механической системы тоже носит пока чисто векторный характер, выступая сегодня в следующем хорошо известном виде: d(Р)/dt = F(e) , где P - полный векторный импульс анализируемой механической системы, а F(e) - векторная сумма действующих на нее внешних сил. Таким образом, именно потому, что главные динамические величины и в основном уравнении механической системы выражаются сегодня не полными кватернионами, как обязательно должно быть, а только мнимыми частями таковых (т. е векторами), и имеет место его анормальная обратимость при инверсии времени. 2) Гармонический осциллятор (в классической механике) — это система, которая при смещении из положения равновесияиспытывает действие возвращающей силы , пропорциональной смещению (согласно закону Гука): где k — положительная константа, описывающая жёсткость системы. Если — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды. Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называютзатухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения. Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания. Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами отклонения), груз на пружине, торсионный маятник и акустические системы. Среди других аналогов гармонического осциллятора стоит выделить электрический гармонический осциллятор (см. LC-цепь). БИЛЕТ №26 1) Сложение скоростей в классической механике. Вариантные и инвариантные величины. 2) Силовое поле. Консервативные и неконсервативные силы. 3)Задача на тему Ответы 1) Относительность движения означает, что траектория, координаты, путь, перемещение, скорость при переходе из одной системы отсчёта к другой могут измениться. Закон сложения перемещений: s{век} = s0{век} + s'{век}, где s{век} - перемещение тела относительно неподвижной системы координат, s0{век} - перемещение подвижной системы координат относительно неподвижной, s'{век} - перемещение тела относительно подвижной системы координат. Закон сложения скоростей. Скорость тела в неподвижной системе отсчёта равна векторной сумме скорости тела в подвижной системе отсчёта и скорости подвижной системы отсчёта относительно неподвижной: v{век} = v0{век} + v'{век}, где где v{век} - скорость тела относительно неподвижной системы координат (абсолютная скорость), v0{век} - скорость подвижной системы координат относительно неподвижной (переносная скорость), v'{век} - скорость тела относительно подвижной системы координат (относительная скорость). При равномерном и прямолинейном движении систем отсчёта относительно друг друга ускорения тела в этих двух системах одинаковы: a{век} = a'{век}. Инвариантные величины - величины не зависящие от выбора системы отсчёта ( неизменные, постоянные, одинаковые ), например, масса (m) Относительные величины - величины зависящие от выбора системы отсчёта. Невозможность передать сигнал со сверхсветовой скоростью непосредственно следует из эйнштейновской формулы сложения скоростей - релятивистской формулы (от англ. relativity - относительность). Задача о сложении скоростей возникает при наличии двух движущихся одна относительно другой инерциальных (то есть движущихся равномерно и прямолинейно) систем отсчета. Состоит она в следующем: если движение некоторого тела или распространение сигнала происходит со скоростью V' в системе S', движущейся в том же направлении относительно системы S со скоростью U, то какова будет скорость V тела (сигнала) для наблюдателя, покоящегося в системе S? В классической кинематике ответ прост: V = V' + U.Например, если поезд (система S') движется относительно платформы (системы S) со скоростью U = 60 км/ч, а в поезде бежит человек в направлении движения поезда со скоростью V ' = 10 км/ч, то скорость перемещения человека относительно платформы будет V= 10 + 60 = 70 км/ч. Релятивис тская же формула сложения скоростей выглядит следующим образом: V = (V' + U)/(1 + V'U/c2). Когда величина скоростей V' и U значительно меньше c (что обычно бывает в привычных нам земных условиях), она переходит в обычную формулу классической механики. Нетрудно также убедиться, что даже если V' = c, то и V = c, то есть ни в какой инерциальной системе невозможно движение со скоростью, превышающей скорость света в вакууме. 2) СИЛОВОЕ ПОЛЕ - часть пространства (ограниченная или неограниченная), в каждой точке к-рой на помещённую туда материальную частицу действует определённая по численной величине и направлению сила, зависящая только от координат х, у, z этой точки. Такое С. п. наз. стационарным; если сила поля зависит и от времени, то С. п. наз. нестационарным; если сила во всех точках С. п. имеет одно и то же значение, т. е. не зависит ни от координат, ни от времени, С. п. наз. однородным. Стационарное С. п. может быть задано ур-ниями  где Fx, Fy, Fz - проекции силы поля F. Если существует такая ф-ция U(x, у, z), называемая силовой ф-цией, что элементарная работа сил поля равна полному дифференциалу этой ф-ции, то С. п. наз. потенциальным. В этом случае С. п. задаётся одной ф-цией U(x, у, z), а сила F может быть определена через эту ф-цию равенствами:  или 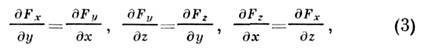 . Условие существования силовой ф-ции для данного С. п. состоит в том, что  или  . При перемещении в потенциальном С. п. из точки M1(x1, y1, z1)в точкуМ2 (х2, у2, z2) работа сил поля определяется равенством и не зависит от вида траектории, по к-рои перемещается точка приложения силы.Поверхности U(x, у, z) = const, на к-рых ф-ция сохраняет пост. значение, наз. поверхностями уровня. Сила в каждой точке поля направлена по нормали к проходящей через эту точку поверхности уровня; при перемещении вдоль поверхности уровня работа сил поля равна нулю. Примеры потенциального С. п.: однородное поле тяжести, для к-рого U = -mgz, где т - масса движущейся в поле частицы, g - ускорение силы тяжести (ось z направлена вертикально вверх); ньютоново поле тяготения, для к-рого U = km/r, где r =  - расстояние от центра притяжения, k - постоянный для данного поля коэффициент. Вместо силовой ф-ции в качестве характеристики потенциального С. п. можно ввести потенциальную энергию П, связанную с U зависимостью П(х, у, z)= = -U(x, у, z). Изучение движения частицы в потенциальном С. п. (при отсутствии других сил) существенно упрощается, т. к. в этом случае имеет место закон сохранения механич. энергии, позволяющий установить прямую зависимость между скоростью частицы и её положением в С. п. с. м. Тарг. СИЛОВЫЕ ЛИНИИ- семейство кривых, характеризующих пространственное распределение векторного поля сил; направление вектора поля в каждой точке совпадает с касательной к С. л. Т. о., ур-ния С. л. произвольного векторного поля А (х, у, z) записываются в виде:  Плотность С. л. характеризует интенсивность (величину) силового поля. Область пространства, ограниченная С. л., пересекающими к--л. замкнутую кривую, наз. силовой трубкой. С. л. вихревого поля замкнуты. С. л. потенциального поля начинаются на источниках поля и заканчиваются на его стоках (источниках отрицат. знака). Консервативные и неконсервативные силы. В современной физике различают четыре вида взаимодействий: I. гравитационная, или взаимодействие, обусловленное всемирным тяготением; II. электромагнитная, которая осуществляется через электрические и магнитные поля; III. сильная или ядерная, которая обеспечивает связь частиц в атомном ядре; IV. слабая, которая отвечает за численные процессы распада элементарных частиц. Мы с вами в рамках классической механики будет иметь дело из гравитационными силами и магнитными силами, а также с упругими силами и силами трения. Два последних вида сил определяются характером взаимодействия между молекулами вещества. Силы взаимодействия между молекулами имеют электромагнитное происхождение. Следовательно, упругие силы и силы трения являются по своей природе электромагнитными. Силы, которые рассматриваются в физике разделяются на консервативные и неконсервативные. Силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным размещением тела в пространстве, называют консервативными, или потенциальными. К ним принадлежат: - силы притяжения - силы упругости - электростатические силы взаимодействия между заряженными телами. Силы будут консервативными при условии когда в системе нет перехода механического движения в другие формы движения материи, или превращения других форм движения в механический. Силы, что не принадлежат к консервативным, называют неконсервативными: - силы трения, которые возникают при скольжении одного тела по поверхности другого - силы сопротивления, которых испытывает тело, двигаясь в жидкой или газообразной среде. Эти силы зависят не только от формы тел, но и от их скорости. Они направлены всегда против направления скорости, потому работа сил трения всегда отрицательна. Гравитационные и электромагнитные силы являются фундаментальными - их нельзя возвести к другим, более простых сил. Упругие силы и силы трения не являются фундаментальными. Законы фундаментальных сил достаточно простые. Убедиться в этом можно из примера. Вспомним определение силы - это мера внешнего действия на тело, которое возникает в процессе его взаимодействия с другим телом. Это физическая величина введена для характеристики передаваемости движению от одного тела к другому, следовательно, изменения движения взаимодействующих тел. Силу нельзя рассматривать оторвано от материи и ее движения. Если под действием нескольких сил тело хранит свое состояние спокойствия, или равномерного прямолинейного движения, то такую систему действующих сил будем называть уравновешенной, или эквивалентной нулю. Результаты действия силы в разных практических примерах более легко объяснить, если различать вслед за Ньютоном статичные и динамические проявления силы. Поэтому различают статичный и динамический способы измерения силы. Результатами статичного проявления силы является давление на тела, которые препятствуют движению, и их деформация. Понятно, что сила, которая оказывается статично, всегда вызывает равную ей по величине и противоположную за направлением реакцию опоры - силу упругой деформации. Результатом динамического проявления силы являются ускорения - тангенциальное или нормальное. В таком случае силу можно определить по второму закону Ньютона. Но почти везде силы обнаруживают частичного как статичные, так и динамические проявления. Следовательно, к консервативным силам относят силы притяжения, силы упругости и силы электростатического взаимодействия; к неконсервативным соответственно - силы трения и силы сопротивления. |