Ответы. Задача по теме Работа. Мощность. Ответы
 Скачать 1.58 Mb.
|
Билет №7. 1)Первый закон Ньютона. Явление инерции. Примеры, масса как мера инертности. 2) Момент инерции полого цилиндра относительно оси совпадающей с осью симметрии. 3)Задача на тему импульс. Ответы: 1)Существуют такие системы отсчёта относительно которых, тело движется равномерно и прямолинейно, если на него не действуют другие тела, такие СО называются инерциальными. Для того чтобы изменилась состояние тела его характер движения, необходимо чтоб на него воздействовали другие тела. Ине́рция — свойство тел сохранять покой или равномерное прямолинейное движение, если внешние воздействия на него отсутствуют или взаимно скомпенсированы, постулируется Первым законом Нью́тона.Примеры Яишницу на сковородке снимаешь с плиты-по инерции жарится, ты бежишь и не можешь резко остановиться потому что мышцы какое то время продолжали двигаться по инерции. 2)  момент инерции.Билет№8. 1)Второй закон Ньютона. Соотношение между первым и вторым. 2)Главные оси. Главные моменты инерции. Теорема Штейнера Гюгенса. 3)Задача по теме энергия. Ответы: 1) Второй закон Ньютона – основной закон динамики. Этот закон выполняется только в инерциальных системах отсчета. Приступая к формулировке второго закона, следует вспомнить, что в динамике вводятся две новые физические величины – масса тела m и сила F а также способы их измерения. Первая из этих величин – масса – является количественной характеристикой инертных свойств тела. Она показывает, как тело реагирует на внешнее воздействие. Вторая – сила F – является количественной мерой действия одного тела на другое. Второй закон Ньютона – это фундаментальный закон природы; он является обобщением опытных фактов, которые можно разделить на две категории: Если на тела разной массы подействовать одинаковой силой, то ускорения, приобретаемые телами, оказываются обратно пропорциональны массам:
Если силами разной величины подействовать на одно и то же тело, то ускорения тела оказываются прямо пропорциональными приложенн силам:
Обобщая подобные наблюдения, Ньютон сформулировал основной закон динамики: Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение:F=ma. Это и есть второй закон Ньютона. Он позволяет вычислить ускорение тела, если известна его масса m и действующая на тело сила F:a=F/m. Во втором законе Ньютона заключен, как частный случай, первый закон, или закон инерции. Действительно, из формулы (a=f/m) видно, что если f=0, то и а=0, т. е. если на тело не действуют силы (или силы действуют, но их равнодействующая равна нулю), то и ускорение равно нулю, и значит, тело сохраняет состояние покоя или равномерного прямолинейного движения. 2) ОСИ ИНЕРЦИИ главные - три взаимно перпендикулярные оси, которые можно провести через любую точку твердого тела, отличающиеся тем, что если тело, закрепленное в этой точке, привести во вращение вокруг одной из них, то при отсутствии внешних сил оно будет продолжать вращаться вокруг этой оси, как вокруг неподвижной. Главные оси и главные моменты инерции твердого тела. При вращательном движении все точки твердого тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Для описания вращательного движения нужно задать положение в пространстве оси вращения и угловую скорость тела в каждый момент времени. Ось, положение которой в пространстве остается неизменным при вращении вокруг нее тела в отсутствие внешних сил, называется свободной осью тела. Можно доказать, что для тела любой формы и с произвольным распределением массы существуют три взаимно перпендикулярные, проходящие через центр инерции тела оси, которые могут служить свободными осями: они называются главными осями инерции. У тела, обладающего осевой симметрией (например, у однородного цилиндра), одной из главных осей инерции является ось симметрии, в качестве двух других осей могут служить две любые взаимно перпендикулярные оси, лежащие в плоскости, перпендикулярной к оси симметрии и проходящие через центр инерции тела. Таким образом, у тела с осевой симметрией фиксирована только одна из главных осей инерции. Моменты инерции относительно главных осей называются главными моментами инерции тела. В общем случае эти моменты различны:  . Для тела с осевой симметрией два главных момента имеют одинаковую величину, третий же, отличен от них:  . В случае тела с центральной симметрией все три главных момента инерции одинаковы:  .Момент инерции в динамике вращательного движения играет ту же роль, что и масса тела в динамике поступательного движения. Но есть и принципиальная разница. Если масса – внутреннее свойство данного тела, не зависящее от его движения, то момент инерции тела зависит от того, вокруг какой оси оно вращается. Для разных осей вращения моменты инерции одного и того же тела различны. Теоре́ма Гю́йгенса — Ште́йнера, или просто теорема момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела JC относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:  .JC — известный момент инерции относительно оси, проходящей через центр масс тела, J — искомый момент инерции относительно параллельной оси, m — масса тела, d — расстояние между указанными осями. Вывод Момент инерции, по определению:  Радиус-вектор можно расписать как разность двух векторов: , где — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:  Вынося за сумму , получим:  Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:  Тогда:  Откуда и следует искомая формула: ,где JC — известный момент инерции относительно оси, проходящей через центр масс тела. БИЛЕТ№9. 1)Взаимодействие тел. Третий закон Ньютона. 2) Свободные оси в твердом теле. Устойчивость свободных осей. 3)Задача на тему Энергия. Ответы: 1) ТРЕТИЙ ЗАКОН НЬЮТОНА В природе никогда не бывает одностороннего действия одного тела на другое, между телами всегда возникает взаимодействие. Взаимодействие между телами может происходить как при соприкосновении, так и без соприкосновения тел. В результате изучения взаимодействия тел, Ньютон открыл третий закон динамики: Силы, с которыми два тела действуют друг на друга, всегда равны по величине и противоположны по направлению. Одна из этих сил называется действующей, а другая - противодействующей. F1=-F2. Эти силы: - действуют вдоль одной прямой; - направлены в противоположные стороны; - равны по величине; - приложены к разным телам, поэтому не уравновешивают друг друга; - одинаковой природы. Главные и свободные оси тела Ось приведенного во вращение твердого тела со временем меняется. Ось вращения, направление которой в пространстве не изменяется с течением времени без действия на неe внешних сил называется свободной осью тела. Можно доказать, что в любом твердом теле существуют три взаимно перпендикулярные оси, проходящие через его центр масс, которые могут служить свободными осями. Эти оси называются главными осями инерции. У тела с центральной симметрией (например, однородный шар) главными осями являются любые три взаимно перпендикулярные оси, проходящие через центр масс. У тела с осевой симметрией (например, однородный цилиндр, конус) одна из главных осей фиксирована (совпадает с осью симметрии). У однородного параллелепипеда главные оси проходят через центры противоположных граней. В 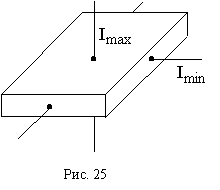 ращение твердого тела устойчиво относительно главной оси с максимальным и минимальным моментами инерции. Вращение неустойчиво относительно главной оси с промежуточным моментом инерции (рис. 25). Например, у прямоугольного параллелепипеда , являются моментами инерции относительно осей, параллельных его самой длинной и короткой сторон. При подбрасывании вверх с вращением относительно этих осей, движение происходит устойчиво. Если вращать относительно третьей оси – параллелепипед совершает беспорядочное движение.Найдем момент внешних сил, который необходимо приложить для удержания несвободной оси тела в неизменном положении. Пусть однородный стержень жестко скреплен с осью вращения в середине (центр масс - точка С на рис. 26). Угол - угол между осью и стержнем, - угловая скорость стержня. Момент внешних сил, который необходимо приложить к оси, чтобы ее направление не менялось Билет№10 1)Импульс тела. Уравнение движение материальной точки. Импульс Силы. 2)Движение твёрдого тела закреплённого в точке. Динамическое уравнение Эйлера. Угол проекции, угол скорости. Проекции на ось xyz. 3)Задача на тему колебания тела. Ответы: p=mV.Произведение массы тела на его скорость называют импульсом (или количеством движения) тела. Импульс тела — векторная величина, так как скорость — вектор. Формула (49.2) выражает закон изменения импульса тела: изменение вектора импульса тела под действием постоянной силы равно произведению силы на время ее действия. Если сила не остается постоянной, то формула (49.2) применима только для таких малых промежутков времени, за которые сила не успевает еще заметно измениться ни по величине, ни по направлению. При большом изменении силы формулой (49.2) также можно пользоваться, но в качестве / следует тогда брать среднее значение силы за рассматриваемый промежуток времени. В случае прямолинейного движения тела формулу (49.2) можно написать в скалярном виде: mv — mv0 = ft. (49.3) В этой формуле, как обычно, разные знаки величин v, v0 и f будут обозначать противоположные направления скоростей и сил. Импульс силы — это мера воздействия силы на тело за данный промежуток времени (в поступательном движении). За конечный промежуток времени он равен определенному интегралу от элементарного импульса силы, где пределами интегрирования являются моменты начала и конца промежутка времени действия силы: В случае одновременного действия нескольких сил сумма их импульсов равна импульсу их равнодействующей за то же время. Любая сила, приложенная даже в доли секунды (например, при отталкивании коньком от льда), имеет импульс (рис. 9). Во вращательном движении момент силы, действуя в течение определенного времени, создает импульс момента силы. , Импульс момента силы — это мера воздействия момента силы относительно данной оси за данный промежуток времени (во вращательном движении). Количество движения 1 — это мера поступательного движения шла, характеризующая его способность передаваться другому телу в виде механического движения. Количество движения тела измеряется произведением массы тела на его скорость: количество движения тела может быть определено, например, по тому, как долго оно движется до остановки под действием измеренной тормозящей силы. Кинетический момент 1 — это мера вращательного движения тела, Характеризующая его способность передаваться другому телу в виде Механического движения. Кинетический момент равен произведению момента инерции относительно оси вращения на угловую скорость тела:Импульс силы и импульс момента силы. 2) Вращение тела вокруг неподвижной точки Название такого вида движения довольно точно его определяет. Часто это движение называют сферическим движением потому, что все точки тела движутся по сферическим поверхностям. Наглядным примером такого движения является волчок, закономерности движения которого лежат в основе гироскопических приборов. 1) Углы Эйлера. Уравнения вращения тела с одной неподвижной точкой.
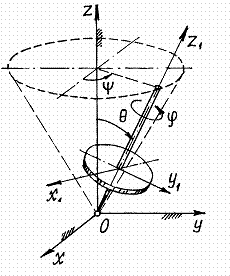
Положение тела определяется тремя углами. Используются различные системы углов. Например, корабельные углы, самолётные углы и др. Но самыми распространёнными являются углы Эйлера: (пси), (тета), (фи). Положение тела определяется следующим образом. Назначаются две системы декартовых осей. Первая система – неподвижные оси . Начало которых берётся в неподвижной точке тела (рис. 20). Вторая система, оси , связывается с телом. Поэтому положение тела будет определяться как положение этих осей относительно неподвижных.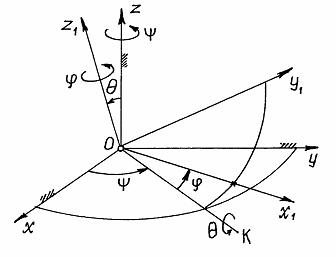 
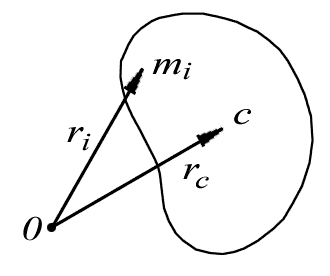
Когда углы Эйлера равны нулю, подвижные оси совпадают с неподвижными. Чтобы определить положение тела, соответствующее заданным углам Эйлера, производим следующие действия. Сначала подвижные оси, а значит и тело, поворачиваем на угол вокруг оси . При этом оси и отойдут от осей и в горизонтальной плоскости и ось займёт положение (рис.20). Затем тело вращаем вокруг нового положения оси (прямой ) на угол . Ось отойдёт от оси на этот угол , а ось приподнимется над горизонтальной плоскостью. Наконец, тело (и подвижные оси) вращаем вокруг нового положения оси на угол . Ось отойдёт от положения в наклонной плоскости, перпендикулярной оси . Это положение тела и будет соответствовать углам Эйлера (на рисунке само тело не показано). Линия пересечения неподвижной плоскости и подвижной , прямая , называется линией узлов. Угол называется углом прецессии, угол – углом нутации, угол – углом собственного вращения. Эти названия углов пришли из теории гироскопов. При движении тела углы Эйлера изменяются по определённым законам  которые называются уравнениями вращения.На примере вращающегося волчка можно лучше разобраться в этих углах Эйлера (рис.21). Ось волчка описывает конус вокруг неподвижной оси . Это вращение определяется углом (говорят: волчок совершает прецессию). Отклонение оси волчка от вертикали – угол нутации . А вращение волчка вокруг своей оси , определяемое углом – собственное вращение. Рис.21 Углы Эйлера определяют три поворота системы, которые позволяют привести любое положение системы к текущему. Обозначим начальную систему координат как (x,y,z), конечную как (X,Y,Z). Пересечение координатных плоскостей xy и XY называется линией узлов N. Угол α между осью x и линией узлов. Угол β между осями z и Z. Угол γ между осью X и линией узлов. Повороты системы на эти углы называются прецессия, нутация и поворот на собственный угол (вращение). Такие поворотынекоммутативны и конечное положение системы зависит от порядка, в котором совершаются повороты. В случае углов Эйлера это последовательность 3,1,3 (Z,X,Z). БИЛЕТ№11. 1)Уравнение движение системы материальных точек. Центр масс. Теорема о движение центра масс. 2)Гироскоп. Свободная и вынужденная прецессии . 3)Задача на тему Ответы: 1)Система материальных точек это совокупность выделенных для рассмотрения решение задач, ещё называется механической системой. Центр масс и система центра масс В любой системе частиц имеется одна замечательная точка С- центр инерции, или центр масс, - которая обладает рядом интересных и важных свойств. Центр масс является точкой приложения вектора импульса системы , так как вектор любого импульса является полярным вектором. Положение точки С относительно начала О данной системы отсчета характеризуется радиусом-вектором, определяемым следующей формулой:
где - масса и радиус-вектор каждой частицы системы, M - масса всей системы (рис. 4.3).
2) Гироско́п(от др.-греч. γυρο «вращение» и др.-греч. σκοπεω «смотреть») — устройство, способное измерять изменение углов ориентации связанного с ним тела относительно инерциальной системы координат. Основные два типа гироскопов по принципу действия: механические гироскопы, оптические гироскопы. По режиму действия гироскопы делятся на: датчики угловой скорости, указатели направления. Однако, одно и то же устройство может работать в разных режимах в зависимости от типа управления. Среди механических гироскопов выделяется ро́торный гироско́п — быстро-вращающееся твёрдое тело, ось вращения которого способна изменять ориентацию в пространстве. При этом скорость вращения гироскопа значительно превышает скорость поворота оси его вращения. Основное свойство такого гироскопа — способность сохранять в пространстве неизменное направление оси вращения при отсутствии воздействия на неё моментов внешних сил. Свойства гироскопа используются в приборах — гироскопах, основной частью которых является быстро вращающийся ротор, который имеет несколько степеней свободы (осей возможного вращения). Прецессия — явление, при котором момент импульса тела меняет своё направление в пространстве под действием момента внешней силы. Углы Эйлера определяют три поворота системы, которые позволяют привести любое положение системы к текущему. Обозначим начальную систему координат как (x,y,z), конечную как (X,Y,Z). Пересечение координатных плоскостей xy и XY называется линией узлов N. Угол α между осью x и линией узлов. Угол β между осями z и Z. Угол γ между осью X и линией узлов. Повороты системы на эти углы называются прецессия, нутация и поворот на собственный угол (вращение). Такие поворотынекоммутативны и конечное положение системы зависит от порядка, в котором совершаются повороты. В случае углов Эйлера это последовательность 3,1,3 (Z,X,Z). Нута́ция (от лат. nūtāre — колебаться) — слабое нерегулярное движениевращающегося твёрдого тела, совершающего прецессию. Напоминает «подрагивание» оси вращения и заключается в слабом изменении так называемого угла нутации между осями собственного и прецессионного вращения тела. Чистая нутация — это такое движение оси вращения, при котором первый угол Эйлера остаётся постоянным. В случае асимметрического волчка описывается траекториями мгновенной угловой скорости волчка |
