Ответы. Задача по теме Работа. Мощность. Ответы

• Название: Задача по теме Работа. Мощность. Ответы
• Анкор: Ответы.doc
• Дата: 14.05.2017
• Размер: 1.58 Mb.
• Имя файла: Ответы.doc
• Тип: Задача; #7583
• страница: 5 из 9

БИЛЕТ№18.

1)Упругое столкновение двух частиц. Лобовой удар.

2)Затухающие колебания.

3)Задача по теме….

Ответы:

1) Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.

Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.

При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.

Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя (рис. 1.21.2).

Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров. Рисунок 1.21.2.

Абсолютно упругий центральный удар шаров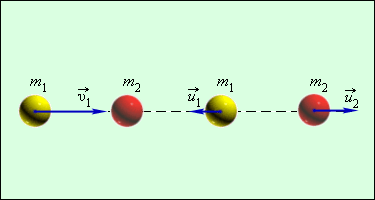
В общем случае массы m1 и m2 соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии 

Здесь υ1 – скорость первого шара до столкновения, скорость второго шара υ2 = 0, u1 и u2 – скорости шаров после столкновения. Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде: 

m1υ1 = m1u1 + m2u2.

Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u1 и u2 шаров после столкновения: 

В частном случае, когда оба шара имеют одинаковые массы (m1 = m2), первый шар после соударения останавливается (u1 = 0), а второй движется со скоростью u2 = υ1, т. е. шары обмениваются скоростями (и, следовательно, импульсами).

Если бы до соударения второй шар также имел ненулевую скорость (υ2 ≠ 0), то эту задачу можно было бы легко свести к предыдущей с помощью перехода в новую систему отсчета, которая движется равномерно и прямолинейно со скоростью υ2относительно «неподвижной» системы. В этой системе второй шар до соударения покоится, а первый по закону сложения скоростей имеет скорость υ1' = υ1 – υ2. Определив по приведенным выше формулам скорости u1 и u2 шаров после соударения в новой системе, нужно сделать обратный переход к «неподвижной» системе.

Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения.

2) Все реальные колебательные системы являются диссипативными. Энергия механических колебаний такой системы постепенно расходуется на работу против сил трения, поэтому свободные колебания всегда затухают - их амплитуда постепенно уменьшается. Во многих случаях, когда отсутствует сухое трение, в первом приближении можно считать, что при небольших скоростях движения силы, вызывающие затухание механических колебаниях, пропорциональны скорости. Эти силы, независимо от их происхождения, называют силами сопротивления. (7.17)

где r - коэффициент сопротивления, v - скорость движения. Запишем второй закон Ньютона для затухающих колебаний тела вдоль оси ОХ 

или(7.18)

Перепишем это уравнение в следующем виде:

и обозначим:

где  представляет ту частоту, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды, т.е. при r = 0. Эту частоту называют собственной частотой колебания системы; β - коэффициент затухания. Тогда

(7.19) Будем искать решение уравнения (7.19) в виде

где U - некоторая функция от t.

Продифференцируем два раза это выражение по времени t и, подставив значения первой и второй производных в уравнение (7.19), получим 

Решение этого, уравнения существенным образом зависит от знака коэффициента, стоящего при U. Рассмотрим случай, когда этот коэффициент положительный. Введем обозначение  тогда С вещественным ω решением этого уравнения, как мы знаем, является функция 

Таким образом, в случае малого сопротивления среды  , решением уравнения (7.19) будет функция

(7.20)

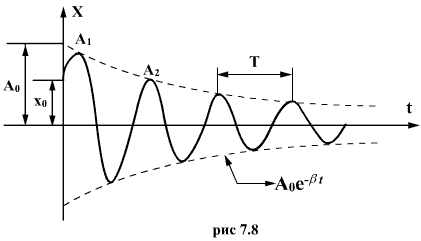График этой функции показан на рис. 7.8. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Величину  называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину  обычно называют периодом затухающих колебаний, правильнее - условным периодом затухающих колебаний,

Натуральный логарифм отношения амплитуд смещений, следующих друг за другом через промежуток времени, равный периоду Т, называют логарифмическим декрементом затухания.



Обозначим через τ промежуток времени, за который амплитуда колебаний уменьшается в е раз. Тогда
откуда

Следовательно, коэффициент затухания есть физическая величина, обратная промежутку времени τ, в течение которого амплитуда убывает в е раз. Величина τ называется временем релаксации.

Пусть N - число колебаний, после которых амплитуда уменьшается в е раз, Тогда



Следовательно, логарифмический декремент затухания δ есть физическая величина, обратная числу колебаний N, по истечению которого амплитуда убывает в е раз

БИЛЕТ№19

1)Движение тел переменной массы. Уравнение Мещерского.

2)Вынужденные колебания. Примеры, уравнение. Резонанс.

3)Задача по теме кинематика вращательного движения.

Ответы:

1) Движение тела переменной массы

В некоторых случаях тел связано с изменением их массы, например масса ракеты уменьшается вследствие истечения газов, образующихся при сгорании топлива, и т. п. 
Произведем вывод уравнения движения тела переменной массы на примере движения ракеты. Если в момент времени t масса ракеты m, а ее скорость v, то по истечении времени dt ее масса уменьшится на dm и станет равной т-dm, а скорость станет равной v+dv. Изменение импульса системы за промежуток времени dt 

 

где u - скорость истечения газов относительно ракеты. Тогда 

 

здесь учтено, что dmdv - малое высшего порядка малости по сравнению с остальными слагаемыми. Если на систему действуют внешние силы, то dp=Fdt, поэтому 

 

или 

(1) 

Второе слагаемое в правой части (1) называют реактивной силой Fp. Если u противоположен v по направлению, то ракета ускоряется, а если совпадает с v, то тормозится. 

Таким образом, мы получили уравнение движения тела переменной массы 

(2) 

которое впервые было выведено И. В. Мещерским (1859-1935). 

Рассмотрим случай отсутвтия воздействия внешних сил на ракету. Положим в уравнении (1) F=0 и будем считать, что скорость выбрасываемых газов относительно ракеты постоянна (ракета движется прямолинейно), получим 

 

откуда 

 

Значение постоянной интегрирования С определим из начальных условий. Если в начальный момент времени стартовая масса m0, а ее скорость ракеты равна нулю, то С = uln(m0). Следовательно, 

 

Это соотношение называется формулой Циолковского. 

Выражения (2) и (3) верны для нерелятивистских движений, т. е. для случаев, когда скорости v и u малы по сравнению со скоростью света в вакууме.



2) Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными.

В этом случае внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.

Периодическая внешняя сила может изменяться во времени по различным законам. Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону с частотой ω, воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте ω0.

Если свободные колебания происходят на частоте ω0, которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят на частоте ω внешней силы.

После начала воздействия внешней силы на колебательную систему необходимо некоторое время Δt для установления вынужденных колебаний. Время установления по порядку величины равно времени затухания τ свободных колебаний в колебательной системе.

В начальный момент в колебательной системе возбуждаются оба процесса – вынужденные колебания на частоте ω и свободные колебания на собственной частоте ω0. Но свободные колебания затухают из-за неизбежного наличия сил трения. Поэтому через некоторое время в колебательной системе остаются только стационарные колебания на частоте ω внешней вынуждающей силы.

Рассмотрим в качестве примера вынужденные колебания тела на пружине (рис. 2.5.1). Внешняя сила  приложена к свободному концу пружины. Она заставляет свободный (левый на рис. 2.5.1) конец пружины перемещаться по закону 

y = ym cos ωt.

где ym – амплитуда колебаний, ω – круговая частота.

Т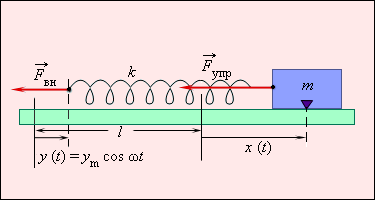акой закон перемещения можно обеспечить с помощью шатунного механизма, преобразующего движение по окружности в поступательно-возвратное движение (рис. 2.5.1).

Вынужденные колебания груза на пружине. Свободный конец пружины перемещается по закону y = ym cos ωt. l – длина недеформированной пружины, k – жесткость пружины

Если левый конец пружины смещен на расстояние y, а правый – на расстояние x от их первоначального положения, когда пружина была недеформирована, то удлинение пружины Δl равно: 

Δl = x – y = x – ym cos ωt.

Второй закон Ньютона для тела массой m принимает вид : 

ma = –k(x – y) = –kx + kym cos ωt.

В этом уравнении сила, действующая на тело, представлена в виде двух слагаемых. Первое слагаемое в правой части – это упругая сила, стремящаяся возвратить тело в положение равновесия (x = 0). Второе слагаемое – внешнее периодическое воздействие на тело. Это слагаемое и называют вынуждающей силой.

Уравнению, выражающему второй закон Ньютона для тела на пружине при наличии внешнего периодического воздействия, можно придать строгую математическую форму, если учесть связь между ускорением тела и его координатой:  Тогдауравнение вынужденных колебаний запишется в виде (**)

где  – собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы. В случае вынужденных колебаний груза на пружине (рис. 2.5.1) величина A определяется выражением: 

Уравнение (**) не учитывает действия сил трения. В отличие от уравнения свободных колебаний (*) (см. §2.2) уравнение вынужденных колебаний (**) содержит две частоты – частоту ω0 свободных колебаний и частоту ω вынуждающей силы.

Установившиеся вынужденные колебания груза на пружине происходят на частоте внешнего воздействия по закону x (t) = xmcos (ωt + θ).

Амплитуда вынужденных колебаний xm и начальная фаза θ зависят от соотношения частот ω0 и ω и от амплитуды m>ymвнешней силы.

На очень низких частотах, когда ω << ω0, движение тела массой m, прикрепленного к правому концу пружины, повторяет движение левого конца пружины. При этом x (t) = y (t), и пружина остается практически недеформированной. Внешняя сила  приложенная к левому концу пружины, работы не совершает, т. к. модуль этой силы при ω << ω0 стремится к нулю. Резонанс — резкое возрастание амплитуды результирующих колебаний при совпадении собственных колебаний системы.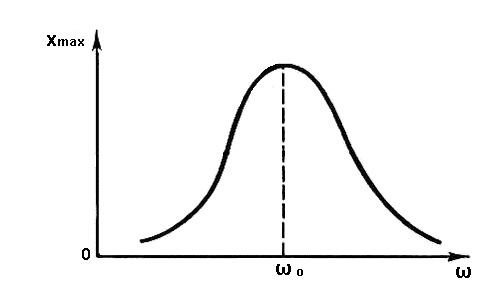




Так как при резонансе внешняя сила совершает за период максимальную положительную работу над колебательной системой, то условие резонанса можно определить как условие максимальной передачи энергии колебательной системе.
Чем меньше трение в системе, тем больше амплитуда вынужденных колебаний при резонансе.
При отсутствии трения амплитуда возрастает со временем неограниченно.

БИЛЕТ№20

1)НИСО. Абсолютное, переносное, относительное движения.

2)Упругие деформации. Механическое напряжение. Модуль Юнга.

3)Задача по теме «Момент инерции».
1)Неинерциальные системы отсчёта.

Неинерциа́льная систе́ма отсчёта — произвольная система отсчёта, не являющаяся инерциальной. Всякая система отсчета, движущаяся с ускорением относительно инерциальной является неинерциальной.

При рассмотрении уравнений движения тела в неинерциальной системе отсчета необходимо учитывать дополнительные силы инерции. Законы Ньютона выполняются только в инерциальных системах отсчёта. Для того, чтобы найти уравнение движения в неинерциальной системе отсчёта, нужно знать законы преобразования сил и ускорений при переходе от инерциальной системы к любой неинерциальной.

Классическая механика постулирует следующие два принципа:

время абсолютно, то есть промежутки времени между любыми двумя событиями одинаковы во всех произвольно движущихся системах отсчёта;

пространство абсолютно, то есть расстояние между двумя любыми материальными точками одинаково во всех произвольно движущихся системах отсчёта.

Эти два принципа позволяют записывать уравнение движения материальной точки относительно любой неинерциальной системы отсчёта, в которой не выполняется Первый закон Ньютона.

Основное уравнение динамики относительного движения материальной точки имеет вид:

,

где  — масса тела,  — ускорение тела относительно неинерциальной системы отсчёта,  — сумма всех внешних сил, действующих на тело,  — переносное ускорение тела,  — кориолисово ускорение тела.

Это уравнение может быть записано в привычной форме Второго закона Ньютона, если ввести фиктивные силы инерции:

 — переносная сила инерции

 — сила Кориолиса

2)Упругие деформации. Модуль Юнга. Коэффициент Пуассона. Закон Гука.

Упругая деформация представляет собой обратимую деформацию, т. е. исходные размеры восстанавливаются после снятия приложенных внешних напряжений. В этом заключается принципиальное отличие упругой деформации от пластической (см. гл. 2.3) и вязкого течения .

В большинстве материалов упругая деформация линейно зависит от приложенного напряжения, особенно при малых напряжениях. Рассматриваемые ниже исключения из этого правила объясняются особенностями структуры.

Обычно предполагают, что упругая деформация возникает мгновенно, в момент приложения внешнего напряжения. Практически это действительно так, поскольку время запаздывания упругой деформации обычно меньше возможностей измерительной аппаратуры. Однако существует ряд особых случаев, когда время запаздывания нельзя игнорировать. Причины более медленной реакции на приложенное напряжение будут рассмотрены ниже в разделе, посвященном неупругости.

В монокристаллах или в материалах с преимущественной ориентировкой упругая деформация анизотропна. Эта анизотропия будет рассмотрена ниже, но без строгого математического доказательства, которое потребовало бы применения тензорного анализа.

Упругое поведение твердых тел зависит от температуры, так как тепловое возбуждение влияет на межатомные связи и на перестройку атомов под действием направленных напряжений. В этом случае молекулярные и атомные твердые тела ведут себя совершенно различно.

Модуль Юнга.

Из трех модулей упругости первым будет рассмотрен модуль Юнга Е, связывающий деформацию ε и одноосное напряжение σ:

ε = σ/E.                                   (2.19)

Это уравнение, часто называемое законом Гука, указывает на линейное соотношение между напряжением и деформацией. Такое предположение представляется обоснованным при деформациях не более 1—2%, т. е. может быть распространено на все твердые тела, за исключением молекулярных, цепи которых могут распрямляться под действием на грузки.

Модуль упругости Е является мерой жесткости. Так как сила связана с напряжением, а изменение расстояния — с деформацией, то мо дуль упругости данного материала может быть найден по наклону кривой, выражающей зависимость действующей силы от расстояния. Наклон этой кривой представляет собой непрерывную функцию и существенно не изменяется при отклонении на 1—2% в ту или другую сторону от равновесного расстояния. Таким образом, величина модуля Юнга оказывается одинаковой при растягивающих и сжимающих напряжениях.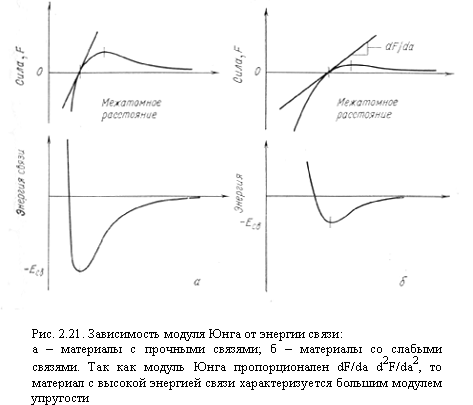




 Значения модуля упругости непосредственно связаны с энергией межатомных связей. Материалы, характеризуемые глубоким и узким минимумом у кривой изменения энергии, имеют большой модуль упругости, так как производная dF/da равна второй производной энергии по расстоянию. Качественно это соотношение вытекает из сравнения рис. 2.21, а и б, данные, приведенные втабл. 2.3, подтверждают его количественно.

Нелинейное соотношение между напряжением и деформацией имеет важное значение для каучуков, у которых из-за распрямления молекулярных цепей упругая деформация может превышать 100%. Приложенные небольшие напряжения вызывают в них значительные деформации (рис. 2.22), но по мере распрямления цепей молекул сопротивление дальнейшему деформированию возрастает, так как дальнейшая деформацияIя требует разрыва связей уже выпрямленных молекул, т. е. нарушения естественной конформации молекул.

Коэффициент Пуассона.

Деформация в одном направлении сопровождается изменением размеров. Согласно рис. 2.23, растягивающее напряжение σzвызывает деформацию по этой оси +εz и сжатие по боковым направлениям -εx и -εy. В случае изотропного материала εх и εy равны.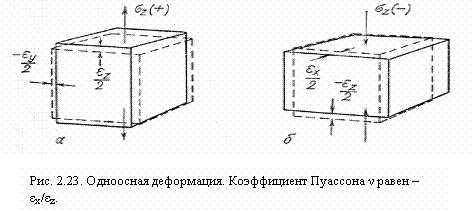




Отношение

ν = -εx/εz (2.20)

 называется коэффициентом Пуассона или коэффициентом поперечного сжатия. Это отношение равно 0,5 для идеального» материала, объем которого при упругом нагружении остается постоянным. Согласно приведенным в табл. 2.4значениям коэффициента Пуассона, на практике такие «идеальные» материалы если и существуют, то встречаются относительно редко.

Объемный модуль упругости.

Всестороннее сжатие  вызывает уменьшение объема ΔV/V, первоначально пропорциональное приложенному давлениюσгидр:

ΔV/V = βσгидр,(2.21а)откудаK = 1/β = σгидр/(ΔV/V).(2.21б)

Здесь β — сжимаемость, а К — объемный модуль упругости, или коэффициент всестороннего сжатия, равный отношению давления к возникающей деформации.

Модуль Юнга и объемный модуль упругости связаны между собой коэффициентом Пуассона. для вывода этого соотношения обратимся к рис. 2.23, б и рассмотрим ступенчатый процесс нагружения, при котором сначала прикладывается напряжение σz, а затем добавляются σx и σy с тем чтобы все три напряжения были равны напряжению σгидр от гидростатического давления. Сначала εz=σz/E. Затем после приложения σx и σy величина σz изменяется на –νεx и -νεy соответственно, в результате чего получаем:

εz = σz/Ε + (-νεx) + (-νεy) = σz/Ε – νσx/Ε –νσy/Ε

и

εz  = [σz – ν(σx +σy)]/Ε                        (2.22)

что представляет собой общую форму закона Гука. Так как при всестороннем сжатии  σгидр=σx=σy=σz, и ΔV/V≈εx+εy+εz=3εz, то ΔV/V=3σгидр(1/2ν)/Ε. Отсюда

Ε = 3Κ(1-2ν).                                     (2.23)

Это соотношение связывает модуль упругости (модуль Юнга)  Е с модулем поперечного всестороннего сжатия (коэффициентом Пуассона) ν и модулем всестороннего сжатия Κ.

Модуль сдвига.

Упругие деформации сдвига γ возникают под действием напряжения сдвига (касательного напряжения) τ. Отношение этого напряжения к деформации называется модулем сдвига:

G = τ/γ.

 Как видно из этого уравнения, модуль сдвига зависит только от свойств образца и не зависит ни от размеров его, ни от формы. Модуль сдвига является величиной размерной и измеряется в динах на сантиметр квадратный (в системе СИ - в Н/м2). Деформацию сдвига можно определить как тангенс угла сдвига α, согласно рис. 2.24:

γ = tg α = x/y.                             (2.25)

Аналогично другим модулям, модуль сдвига является постоянным при обычно встречающихся деформациях, если они меньше пластической деформации, т. е. если между деформацией и силой существует прямая пропорциональность [1].

Путем несложных выкладок можно было бы показать, что модуль сдвига связан с модулем Юнга посредством коэффициента Пуассона:

G = E/2(1+γ).                         (2.26а)

С учетом уравнений (2.23) и (2.26) получаем

Так как коэффициент Пуассона всегда меньше 0,5 и обычно составляет 0,3, то модуль сдвига, как правило, равен 35—40% модуля Юнга Е [1].
3)Задача по теме момент импульса.